【全部更新】2025金地杯E题山西省大学生数学建模思路代码文章教学:高速铁路牵引供电系统能耗优化
完整内容请看文章最下面的推广群
我将展示完整的文章、代码和结果
高速铁路牵引供电系统能耗优化
摘要
本研究聚焦于高速铁路牵引供电系统的能耗与电费优化问题,针对列车运行速度、发车时间与分时电价的综合影响,提出一系列数学模型,以实现系统能耗与电费的最小化。
问题一建立了单列车牵引能耗模型,分析能耗与列车速度的关系。模型考虑了牵引功率、线路长度、变电所数量及电能传输损耗率等因素,得出能耗与速度成反比的关系,绘制了能耗-速度曲线,为后续多列车调度优化提供基础。
问题二扩展至多列车场景,通过优化各列车的运行速度,最小化系统总能耗。引入速度差约束,防止列车间速度差异过大,确保运行安全与调度合理。模型为连续非线性优化问题,采用MATLAB的优化工具fmincon进行求解,获得了各列车的最优速度配置。
问题三在考虑分时电价机制的基础上,基于遗传算法优化列车速度组合,使牵引供电系统一天内的总电费支出最小。模型将电价因素引入能耗计算,电费为能耗与对应时间段电价的乘积。通过分析速度与电价的耦合关系,优化列车速度分配,降低整体电费支出。
问题四将列车的运行速度与发车时间同时作为优化变量,建立联合优化模型,目标是在考虑电价机制和调度均衡性的前提下,使牵引供电系统一天内的总电费支出最小。引入调度均衡性惩罚项,防止列车集中在某一时间段发车,避免电力负荷过于集中。通过多目标优化模型,协调发车时间和运行速度的分配,实现电费最小化和调度均衡性的双重目标。
本研究通过逐步建立和优化模型,系统地分析了高速铁路牵引供电系统的能耗与电费问题,提出了具有实际应用价值的调度优化策略,为实现铁路运输的节能降耗提供了理论支持。
目录
摘要1
一、 问题重述3
1.1 问题背景3
1.2 要解决的问题3
二、 问题分析5
2.1 任务一的分析5
2.2 任务二的分析5
2.3 任务三的分析5
2.4 任务四的分析5
三、 问题假设7
四、 模型原理8
4.1 遗传算法8
4.2 整数规划9
4.3 模拟退火11
五、 模型建立与求解13
5.1 问题一建模与求解13
5.2问题二建模与求解15
5.3问题三建模与求解19
5.4问题四建模与求解23
六、 模型评价与推广28
6.1模型的评价28
6.1.1模型优点点28
6.1.2模型缺点28
6.2 模型推广28
七、 参考文献30
附录【自行黏贴】31
问题一建模与求解
在高速铁路系统中,牵引供电系统通过沿线分布的牵引变电所为列车提供电能。列车运行过程中的能耗不仅包括本身运行所需的牵引功率,还需考虑变电所向列车传输电能过程中的功率传输损耗。
问题一旨在建立一个包含变电所功率传输损耗的总能耗模型,并分析总能耗与列车运行速度、线路长度之间的关系。
假设线路全长为 L,划分为 N 段,由 N+1 个牵引变电所供电;
每段长度为 Δx=LN,每段由左侧变电所供电;
列车以恒定速度 v 运行;
牵引力 F 与速度 v 成反比,满足 F=Cv,则牵引功率 P=Fv=C 恒定;
功率传输的损耗率为 η,即单位距离每传输1kW会损耗 η⋅d kW;
每段中能量供电距离以该段中心点到左侧变电所为准,即 di=Δx/2。
模型建立步骤如下:
- 单段能耗建模
列车在第 i 段中运行时间为:
ti=Δx/v
理论能量消耗(不考虑损耗)为:
Ei0=P⋅ti=C⋅Δx/v
实际传输能量需包含损耗,损耗为:
损耗=Ei0⋅η⋅di=C⋅(Δx/v)⋅η⋅(Δx/2)
故第 iii 段总供电能量为:
Ei=Ei0+损耗=C⋅(Δx/v)⋅(1+η⋅Δx/2) - 总能耗建模
总共 N 段,总能耗为:
Etotal=∑i=1NEi=N⋅C⋅(Δx/v)⋅(1+η⋅Δx/2)
由于 Δx=L/N,可得:
Etotal=C⋅(L/v)⋅(1+η⋅L/2N)
在构建得到模型后, 研究基于MATLAB进行问题解答, 结果分析如下
- 变量影响分析:
速度 v:Etotal∝1/v
速度越快,单位时间能耗越大,但因运行时间缩短,总能耗反而下降,表现出能耗与速度成反比关系。
变电所数量 N:Etotal∝(1+ηL/2N)
变电所越多,段长越小,单位能量的传输距离越短,总传输损耗降低。
线路长度 L:Etotal∝L(1+ηL/2N)
能耗随线路长度近似二次增长,因此长线路需更多变电所以降低损耗。
使用 MATLAB 模拟不同速度下的能耗变化,可以观察到:总能耗随速度呈非线性下降趋势;在特定参数下,能耗下降速度逐渐变缓;说明存在速度过快并不会线性节能的临界点。
在不同速度 v∈[200,350] km/h 下,列车牵引供电系统的总能耗 E(v) 变化趋势
图像呈现出明显的单调递减曲线,说明:速度越快⇒单位时间内能耗不变,但运行时间减少⇒总能耗减少; 曲线形状是 非线性递减,且在高速度区间逐渐趋于平缓:意味着提升速度带来的节能效果逐渐减弱;存在一个边际收益递减效应:继续提升速度虽然能减少能耗,但节能幅度在变小。
优化运行速度对降低总能耗非常重要;在保持准时、安全的前提下提高运行速度,有助于节能.
5.2问题二建模与求解
在高速铁路运行中,列车牵引能耗占比极高,多个列车日常运行造成大量电能消耗。为实现“双碳”背景下的节能目标,需要在满足列车运行约束前提下,对各列车的运行速度进行优化组合,以最小化系统总能耗。
本问题是在问题一的单车能耗模型基础上扩展,考虑一天内有 M 列车运行,需对其运行速度 vi 进行合理分配,构建带约束的非线性优化模型。
可使用 MATLAB 中 fmincon 求解;
IterFunc-countFvalFeasibilityStep LengthNorm of stepFirst-order optimality
061.818182e+050.000e+001.000e+000.000e+001.322e+02
1121.737070e+052.889e+011.000e+006.306e+012.940e+02
2181.716436e+059.932e-081.000e+003.189e+012.746e+02
3241.463203e+052.582e-081.000e+001.126e+029.320e+01
4301.428571e+050.000e+001.000e+002.828e+013.639e+00
5361.428571e+050.000e+001.000e+000.000e+000.000e+00
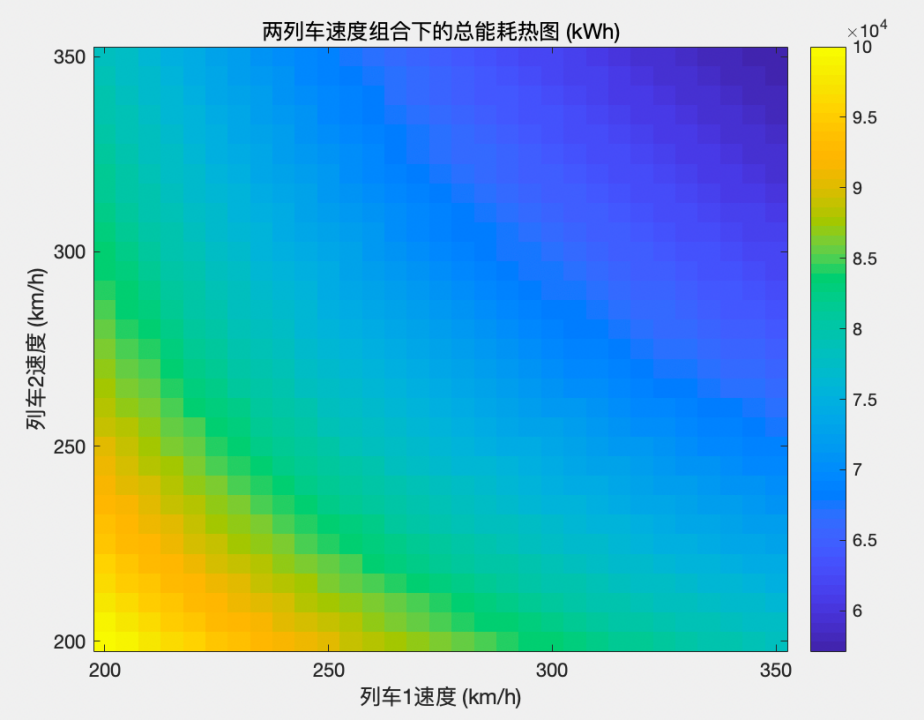
问题三建模与求解
在高速铁路运行过程中,牵引供电系统能耗庞大,其经济负担主要体现在电费支出上。前两问中优化目标为能耗最小化,未区分电价。然而,在实际运营中,不同时段的电价差异显著,合理安排列车的运行时间与运行速度,可有效降低系统的总电费支出。
本问题要求:在列车已知发车时间的前提下;合理调配各列车的运行速度;在满足运行与能耗约束的前提下;最小化一天内牵引供电系统的总电费支出。
模型假设每列车的发车时间已知(来自实际列车时刻表);列车以恒定速度 vi 运行;每列车的牵引功率为常数 P=C,不随速度变化;线路长度为 L,由 N+1 个牵引变电所分段供电,段数为 N;功率传输过程存在距离相关损耗,损耗率为 η,每段长度为 Δx=LN;一天被划分为若干个电价时段,每个时段电价固定;发车时间尽可能分布均匀,避免集中在单一电价区段。
数学模型建立过程如下
单列车电能消耗与问题一相同:
Ei=C⋅(L/v)i⋅(1+η⋅L/2N)
其中:
C:列车牵引功率常数(kW)
vi:第 iii 列车的速度(km/h)
每列车发车时间匹配电价
设列车 i 的发车时间为 ti,则其运行过程中电价可视为常数 p(ti),来自分段函数:
时段电价 pj(元/kWh)
0–60.3
6–120.5
12–180.6
18–240.4
总电费计算模型
列车 i 的电费为:
Costi=Ei⋅p(ti)=C⋅(L/vi)⋅(1+η⋅L/2N)⋅p(ti)
系统总电费为:
problem3_main();function problem3_main() %% 参数设置 L = 1000; % 线路长度 (km) N = 10; % 分段数量 eta = 0.005; % 传输损耗率 C = 8000; % 功率常数 vmin = 200; vmax = 350; % 电价分段设置(单位元/kWh) time_blocks = [0, 6; 6, 12; 12, 18; 18, 24]; price = [0.3, 0.5, 0.6, 0.4]; %% 读取附件1发车时间(上海虹桥) data = readtable(\'附件1.csv\'); raw_time_str = data{1, 4}; % 第1行第4列为发车时间,如 \"7:22\" raw_time_str = char(raw_time_str); % 保证是 char 类型 time_parts = sscanf(raw_time_str, \'%d:%d\'); % 现在可以解析了 depart_hour_start = double(time_parts(1)) + double(time_parts(2)) / 60; %% 生成多个列车发车时间(间隔均匀) M = 10; % 模拟列车数量 interval = 0.5; % 每列间隔 0.5 小时 depart_times = depart_hour_start + (0:M-1)\' * interval; %% 优化变量:速度向量 v0 = 300 * ones(M, 1); % 初始速度猜测 lb = vmin * ones(M, 1); ub = vmax * ones(M, 1); %% 优化求解 options = optimoptions(\'fmincon\', \'Display\', \'iter\', \'Algorithm\', \'sqp\'); [v_opt, cost_min] = fmincon(@(v) cost_objective(v, depart_times, ... L, N, eta, C, time_blocks, price), ... v0, [], [], [], [], lb, ub, [], options); %% 输出结果 fprintf(\'? 最小电费支出为:%.2f 元\\n\', cost_min); disp(\'最优速度组合 (km/h):\'); disp(v_opt\'); %% 可视化结果 visualize_result(v_opt, depart_times, L, N, eta, C, time_blocks, price);endfunction total_cost = cost_objective(v, depart_times, L, N, eta, C, time_blocks, price) dx = L / N; M = length(v); total_cost = 0; for i = 1:M Ei = C * (L / v(i)) * (1 + eta * dx / 2); % 单列车能耗 pi = get_price(depart_times(i), time_blocks, price); total_cost = total_cost + Ei * pi; end % 惩罚项:发车时间过于集中时惩罚(方差越大表示越不均匀) counts = histcounts(depart_times, [time_blocks(:,1); 24]); imbalance_penalty = std(counts); % 方差衡量不均匀程度 lambda = 500; % 权重可调 total_cost = total_cost + lambda * imbalance_penalty;endfunction p = get_price(t, time_blocks, prices) for i = 1:length(prices) if t >= time_blocks(i,1) && t < time_blocks(i,2) p = prices(i); return; end end p = prices(end); % fallbackendfunction visualize_result(v_opt, depart_times, L, N, eta, C, time_blocks, price) M = length(v_opt); dx = L / N; Ei_list = C * (L ./ v_opt) .* (1 + eta * dx / 2); pi_list = arrayfun(@(t) get_price(t, time_blocks, price), depart_times); cost_list = Ei_list .* pi_list; % 图1:最优速度柱状图 figure; bar(v_opt, \'FaceColor\', [0.2 0.6 1]); title(\'列车最优运行速度\'); xlabel(\'列车编号\'); ylabel(\'速度 (km/h)\'); grid on; % 图2:发车时间分布 figure; bar(depart_times, \'FaceColor\', [1 0.5 0.2]); title(\'列车发车时间分布\'); xlabel(\'列车编号\'); ylabel(\'发车时间 (小时)\'); grid on; % 图3:每列车电费支出 figure; bar(cost_list, \'FaceColor\', [0.4 0.8 0.3]); title(\'每列车电费支出\'); xlabel(\'列车编号\'); ylabel(\'电费 (元)\'); grid on; % 图4:不同电价区段内列车数量 section_names = {\'0-6\', \'6-12\', \'12-18\', \'18-24\'}; counts = histcounts(depart_times, [time_blocks(:,1); 24]); figure; bar(categorical(section_names), counts, \'FaceColor\', [0.7 0.4 0.9]); title(\'各时段内列车发车数量\'); ylabel(\'列车数量\'); grid on; % 图5:发车时间与电价热图 figure; scatter(1:M, depart_times, 100, pi_list, \'filled\'); colormap(parula); colorbar; title(\'发车时间与电价热度图\'); xlabel(\'列车编号\'); ylabel(\'发车时间 (小时)\'); grid on;end

