动态规划——线性DP

宝......(✿◡‿◡)

宝，最近流量巨低，求这期大家帮我点到20赞，求求了嘻嘻，这对我真的巨重要！！！

流量低的赞数还不如沃第一篇博文捏，好好开始讲解，线性DP，要想我呀

我与神明画押，神明骂我sha X （非学术）

上来就说DP，可能不太好吸收呢，emmmm，我们先来举个例子：

相信大家都知道“斐波那契数列”的吧

递归版本

long long F(int n) {            if (n == 1 || n == 2) return 1;             else return F(n - 1) + F(n - 2);}

炸一看时间复杂度：

显而易见有大量重复运算，太垃圾了！！！

这可怎么整？有的宝子们已经想到啦！！！咳咳，不是递归用不起，而是递推等有性价比！！！

那就随口说下递推：

递推算法是一种用若干步可重复运算来描述复杂问题的方法。递推是序列计算中的一种常用算法。通常是通过计算机前面的一些项来得出序列中的指定项的值。

用已知项推导未知项时要满足 无后效性

1.已知项已经确定了

2.后面无论发生什么，当前已知项不能再发生变化

递推版本

int a[100]= {0,1,1};long long F(int n) {    if (n == 1 || n == 2) return 1;    for(int i=3; i<=n; i++)        a[i]=a[i-1]+a[i-2];    return a[n];}

再看一眼复杂度：O（N）

哇，可太有生活了！！！为什么递推就如此高效迅猛？递推有没有什么缺点？

咳咳，递推就是动归的祖先，先不多多介绍，我看看题及可：

方法1——暴力

我们可以使用dfs(枚举)从上往下走，求出所有路径的和，求出最大值。

复杂度：设层数是n，每层两条路，共2^(n-1)条路

优点：好写

缺点：慢死(我等的黄花菜都凉了)

方法2——贪心

我们可以显而易见思考“路径上的所有数字的和的最大值是多少?

这不是可以贪心嘛！

这里再随口嗦一下贪心：

贪心策略：既然总路径和要最大，那每次二选一的时候尽量选大的呗！

通过样例观察， 21（1+3+6+11），合理！

方法3——暴力的优化，递推

参考引例，我们把重复计算的部分存起来，每项只算一次，复杂度显而易见会变成O(N2)

精髓：存储代替运算

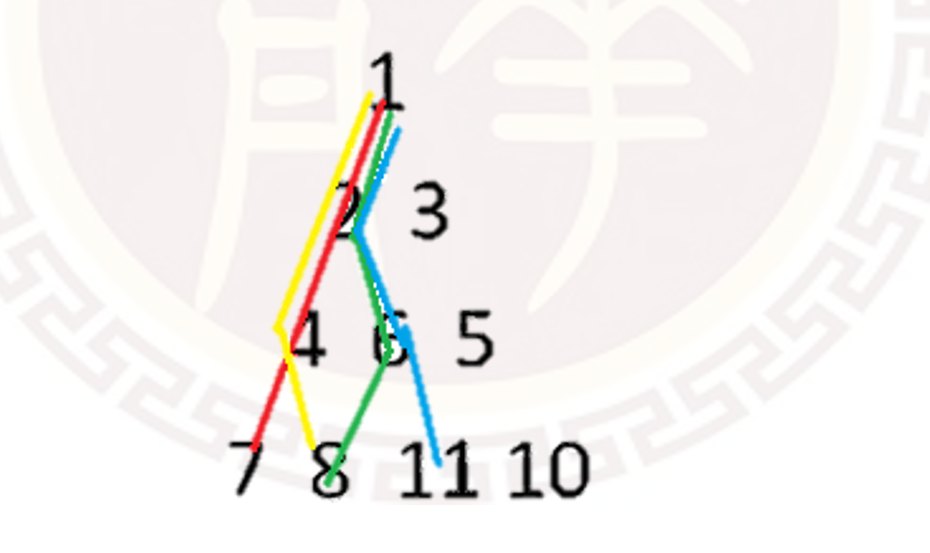
（鼠标握不住，划拉的不好看）

动态规划初期步骤：

第零步：

确定属性 有几个能影响求解的参数，那就有几个属性，用来存储解的dp数组就有几维，每一维代表一个属性。

问题求什么dp数组里就存什么

例题中：

影响到路径和的是路径中选取哪些数。对于矩阵的数来说要有行有列。即用第i行第j列表示,dp[i][j]。

问题是求路径和最大值,即dp数组中存储的是能选择到的最大值。

第一步：

确定状态 先读一遍原问题，参照原问题的句式读一遍现在的dp数组。会发现现在的dp数组只是一个缩小版的原问题（子结构）。

例题中：

原问题：从顶点到底边上的某个点的路径和的最大值是多少 状态：dp[i][j]从顶点到第i行第j列的路径和最大值是多少

第二步：

状态转移方程 当前状态可以由哪些状态一步递推得到，从这些状态中选择一个最好的状态（最优子结构）或者选择状态的叠加，再加上当前这一步的递推变化

例题中：

当前的dp[i][j]可以由dp[i-1][j]或者dp[i-1][j-1]走一步得到，选取二者中较大的，再加上当前a[i][j]递推得到 方程：dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j];

附加步：注意事项

1.可能会爆空间

2.dp只能存储最优解，但是不知道最优解的构成。

2.1部分构成:修改状态定义/存储

2.2区别状态:多开一维

2.3全部构成:f[][]存储从哪转移的

3.dp数组的下标往往出现减法，注意RE

4.记得初始化

5.注意无后效性

DP的主要内容就这些，宝贝们，把赞赞冲破20个呀，我是雨晴，洛谷账号：qwe777

练习：

P1216 数字三角形         模板

P1002 过河卒            注意边界

P1192 台阶问题        简单题

P1095 守望者的逃离        分类讨论

P1115 最大子段和        DP构成

进接题：

再见，点个zan吧，我的宝.....