LeetCode51~70题解
LeetCode51.N皇后:
题目描述:
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例 1:
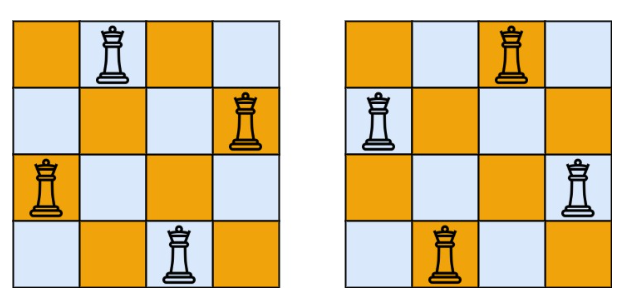
输入:n = 4
输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[[“Q”]]
提示:
1 <= n <= 9
思路:
由题意得知: 同一行同一列并且对角都不能出现两个皇后,同一列和同一行都很好判断,问题是对角线上的判断,怎么看这条对角线之前有没有放过皇后呢? 这里使用对角线的一般公式:y = x + b 以及 y = -x + b 来将同一对角线映射到数组中的同一下标,即该对角线就对应一个数组下标,使用bool数组进行维护,如果该对角线放置过皇后那么对应数组下标对应的标记置为true表示这条对角线已经放过皇后不能再放 ,于是最后按行(或列)进行分层,进行dfs递归遍历,对每一行(或每一列)的每一个位置进行放置判断,以此搜索路径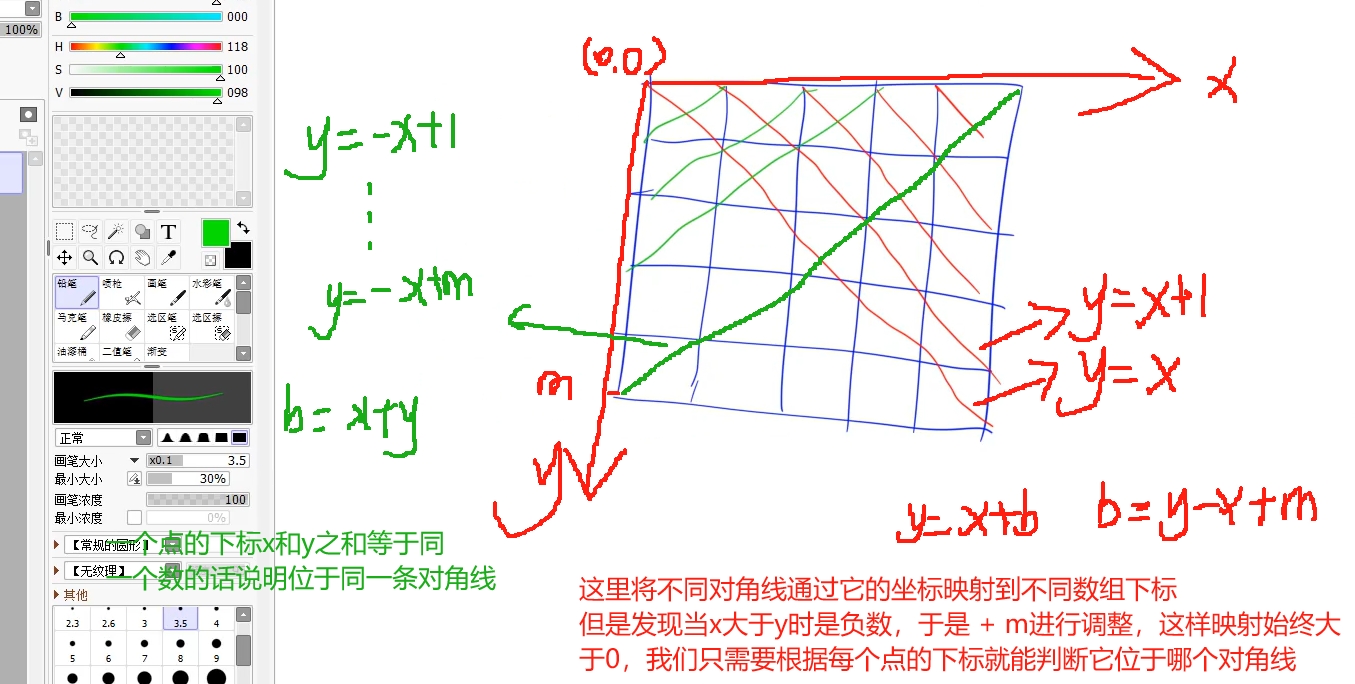
注释代码:
class Solution {public: int m; vector col, dg, udg; vector<vector> res; vector path; vector<vector> solveNQueens(int n) { m = n; //记录多少行 //初始化各个容器 col = vector(m); dg = vector (m * 2); udg = vector (m); path = vector(n, string(n, \'.\')); //将路径初始化为\'.\' dfs(0); //从第0行开始爆搜 return res; } void dfs(int u ) { //如果u == 行数,说明已经找完了一种方案 if(u == m) { res.push_back(path); return; } //每一列进行皇后放置 for(int i = 0; i < m; i++) { if(!col[i] && !dg[m + u - i] && !udg[u + i]) { col[i] = dg[m + u - i] = udg[u + i] = true; path[u][i] = \'Q\'; dfs(u + 1); path[u][i] = \'.\'; col[i] = dg[m + u - i] = udg[u + i] = false; } } }};纯享版:
class Solution {public: int m; vector row, dg, udg; vector<vector> res; vector path; vector<vector> solveNQueens(int n) { m = n; row = vector (m); dg = udg = vector (m * 2); path = vector(m, string(n, \'.\')); dfs(0); return res; } void dfs(int u) { if(u == m) { res.push_back(path); return; } for(int i = 0; i < m; i++) { if(!row[i] && !dg[u - i + m] && !udg[i + u]) { row[i] = dg[u - i + m] = udg[i + u] = true; path[i][u] = \'Q\'; dfs(u + 1); row[i] = dg[u - i + m] = udg[i + u] = false; path[i][u] = \'.\'; } } }};LeetCode52.N皇后Ⅱ:
题目描述:
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1: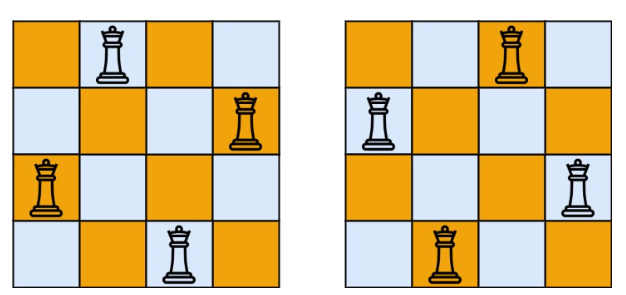
输入:n = 4
输出:2
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 9
思路:
跟上题完全一样,只不过是返回方案数,只需要对方案进行统计
注释代码:
class Solution {public: int m; vector row, dg, udg; vector<vector> res; vector path; int totalNQueens(int n) { m = n; row = vector (m); dg = udg = vector (m * 2); path = vector(m, string(n, \'.\')); dfs(0); return res.size(); } void dfs(int u) { if(u == m) { res.push_back(path); return; } for(int i = 0; i < m; i++) { if(!row[i] && !dg[u - i + m] && !udg[i + u]) { row[i] = dg[u - i + m] = udg[i + u] = true; path[i][u] = \'Q\'; dfs(u + 1); row[i] = dg[u - i + m] = udg[i + u] = false; path[i][u] = \'.\'; } } }};LeetCode53.最大子序和:
题目描述:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
算法1思路:动态规划:
集合f[i] 表示所有以nums[i]结尾的区间中的最大和 为了得出状态转移方程对f[i]集合进行划分为 区间长度大于2 和 nums[i]本身 两类,通过比较发现 f[i] 就是求 区间长度大于2 和nums[i] 两者之间的最大值,而区间长度大于2的区间中,都是以i为结尾,那么可以将所有区间中的nums[i]单独拿出来,发现剩余区间组成就是f[i -1]的集合表示,那么f[i] = max{f[i - 1] + nums[i], nums[i]} 而两者都有nums[i],所以可以将nums[i]拿出来变成:f[i] = nums[i] + max(f[i - 1], 0) 由转移方程可知,f[i] 的状态之跟f[i - 1]有关,所以为了节省空间消耗可以使用变量last来维护上一个状态的值,并在下一个状态利用上一个状态的值更新本次状态: last = nums[i] + max(last, 0)
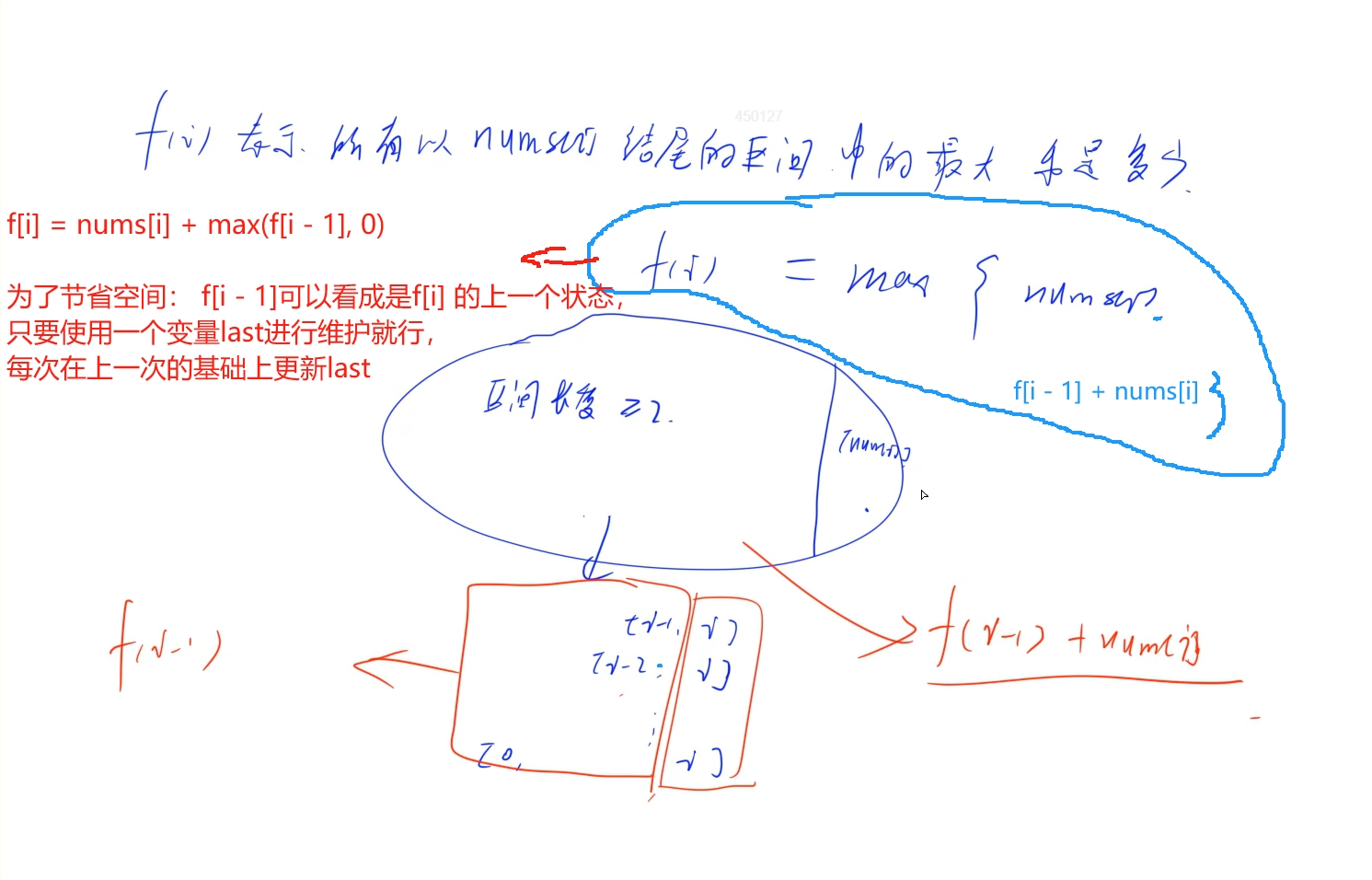
时间复杂度:O(n)
只对数组进行了一次循环操作
空间复杂度: O(1)
未开数组维护状态集合,只是使用了变量维护上个状态值
算法1(动态规划):
class Solution {public: int maxSubArray(vector& nums) { int res = INT_MIN; for(int i = 0, last = 0; i < nums.size(); i++) { last = nums[i] + max(last, 0); res = max(res, last); } return res; }};纯享版:
LeetCode54.螺旋矩阵:
题目描述:
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
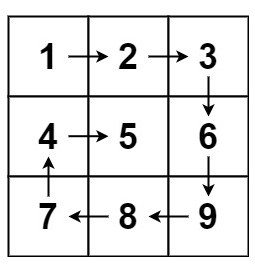
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2: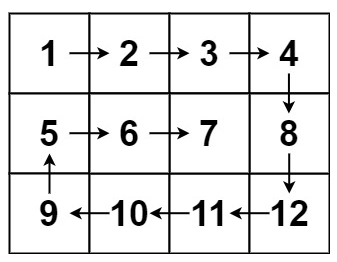
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100
思路:
利用方向数组 算法基础课中的蛇形矩阵是一样的题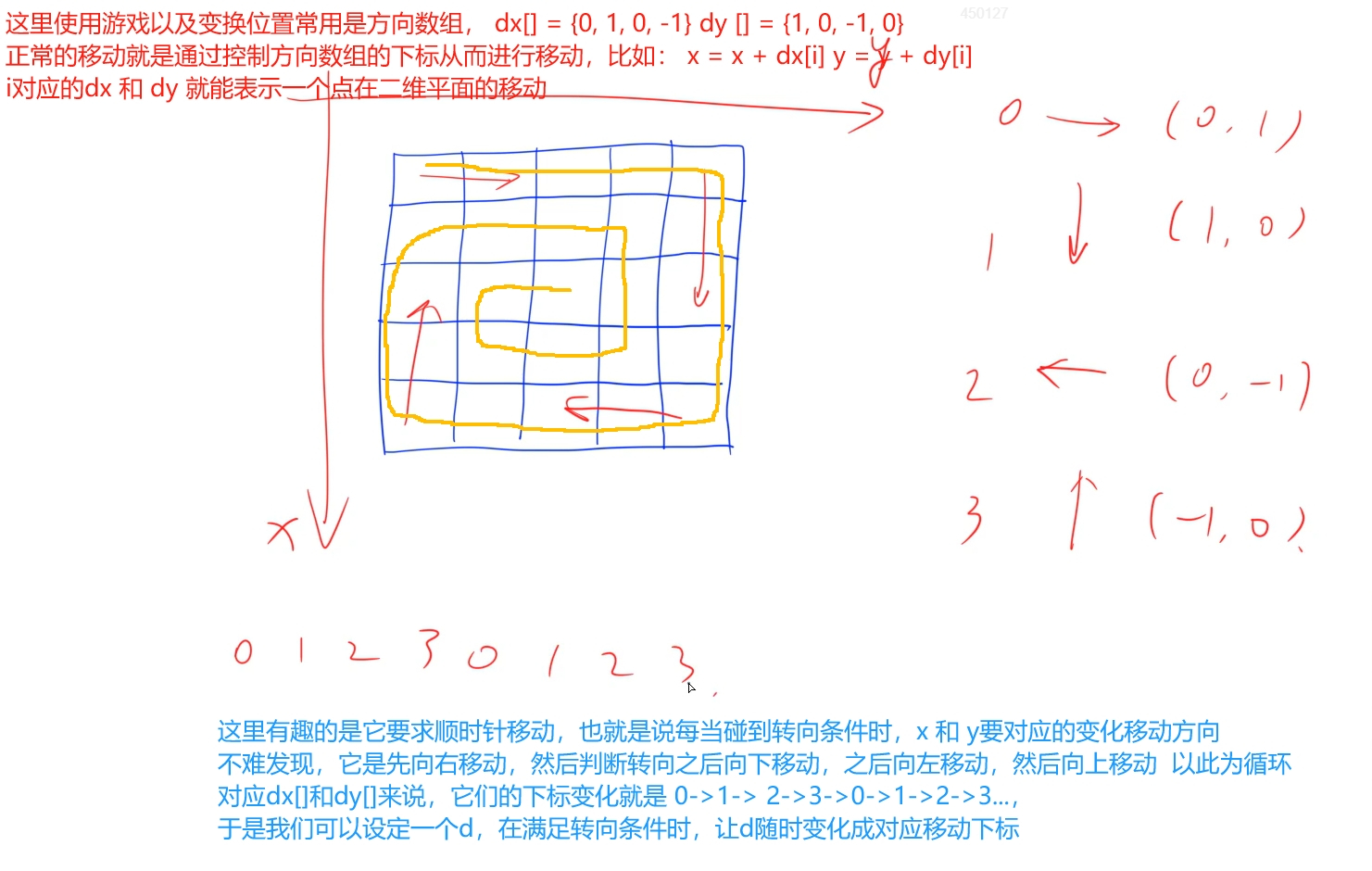
注释代码:
class Solution {public: vector spiralOrder(vector<vector>& matrix) { vector res; int n = matrix.size(); //记录行 if(!n) return res; int m = matrix[0].size(); //记录列 int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; //定义方向数组 vector<vector> st(n, vector(m)); //从头开始走 for(int i = 0, x = 0, y = 0, d = 0; i < n * m; i++) { res.push_back(matrix[x][y]); st[x][y] = true; int a = x + dx[d], b = y + dy[d]; //发生越界或者下一个位置已经走过时,改变方向 if(a = n || b = m || st[a][b]) { //顺时针改变方向 d = (d + 1) % 4; //记录改变之后的位置 a = x + dx[d], b = y + dy[d]; } //将走的位置更新 x = a, y = b; } return res; }};纯享版:
class Solution {public: vector spiralOrder(vector<vector>& matrix) { vector res; int n = matrix.size(); if(!n) return res; int m = matrix[0].size(); vector<vector> st(n, vector(m)); int dx[] = {0, 1, 0, -1}, dy[]= {1, 0, -1, 0}; int x = 0, y = 0, d = 0; for(int i = 0; i < n * m; i++) { res.push_back(matrix[x][y]); st[x][y] = true; int a = x + dx[d], b = y + dy[d]; if(a = n || b = m || st[a][b]) { d = (d + 1) % 4; a = x + dx[d], b = y + dy[d]; } x = a, y = b; } return res; }};LeetCode55.跳跃游戏:
题目描述:
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 10^4
0 <= nums[i] <= 10^5
思路:
贪心思想,但本质是动态规划:设定f[i] 表示位置i能跳到的最远位置,所以f[i] = max(f[i - 1], i + nums[i]),由状态转移矩阵可知f[i]的状态只跟f[i -1]有关,所以可以用常量last来存储状态
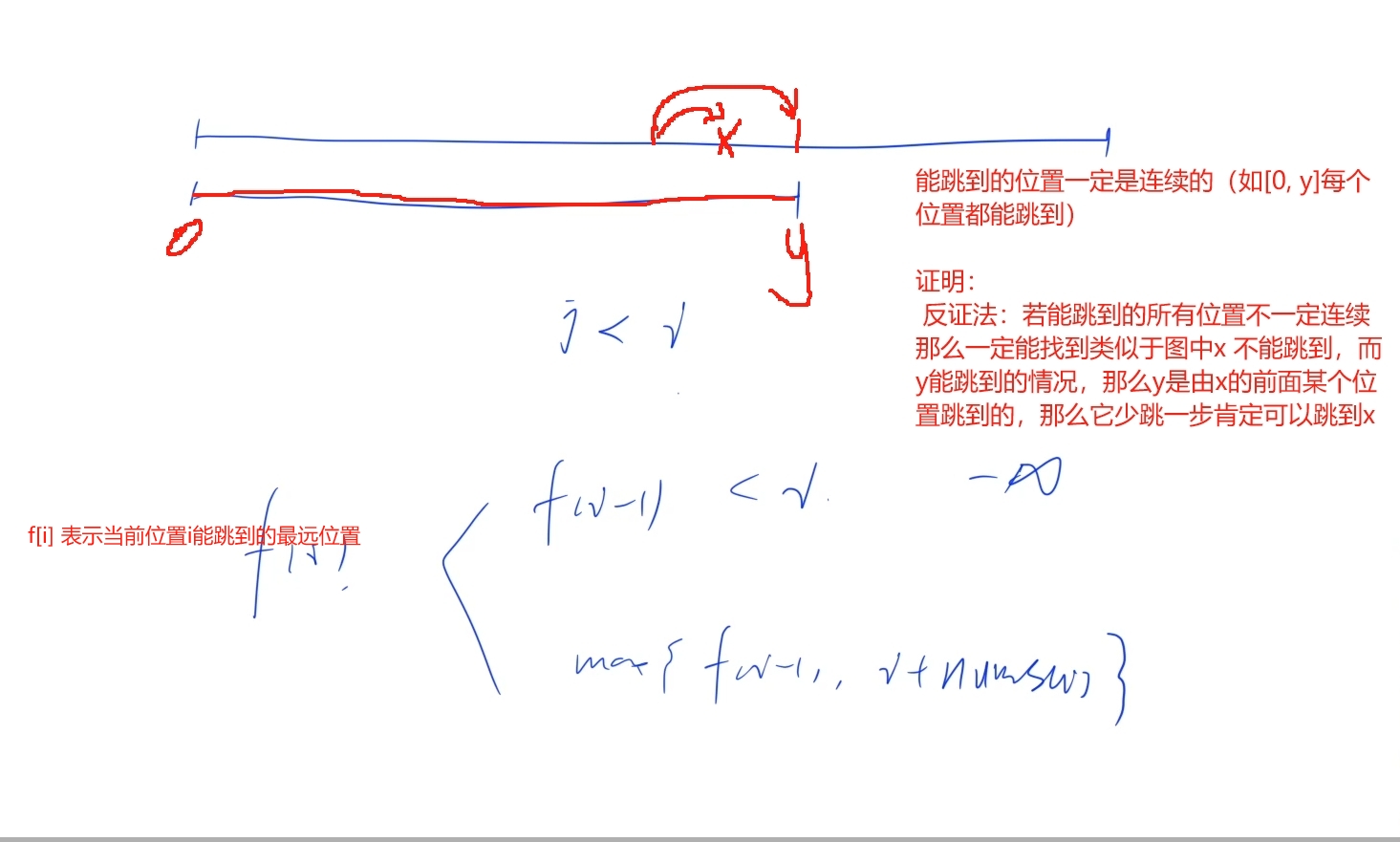
注释代码:
class Solution {public: bool canJump(vector& nums) { int last = 0; for(int i = 0; i < nums.size(); i++) { // if(last < i) return false; //如果上一次无法跳到当前位置,那么下一步就无法继续 //看最远能跳到哪个位置,是上一个位置还是当前位置的基础上加上当前一跳 last = max(last, i + nums[i]); } return true; }};纯享版:
class Solution {public: bool canJump(vector& nums) { int last = 0; for(int i = 0; i < nums.size(); i++) { if(last < i) return false; last = max(last, i + nums[i]); } return true; }};LeetCode56.合并区间:
题目描述:
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= starti <= endi <= 10^4
思路:
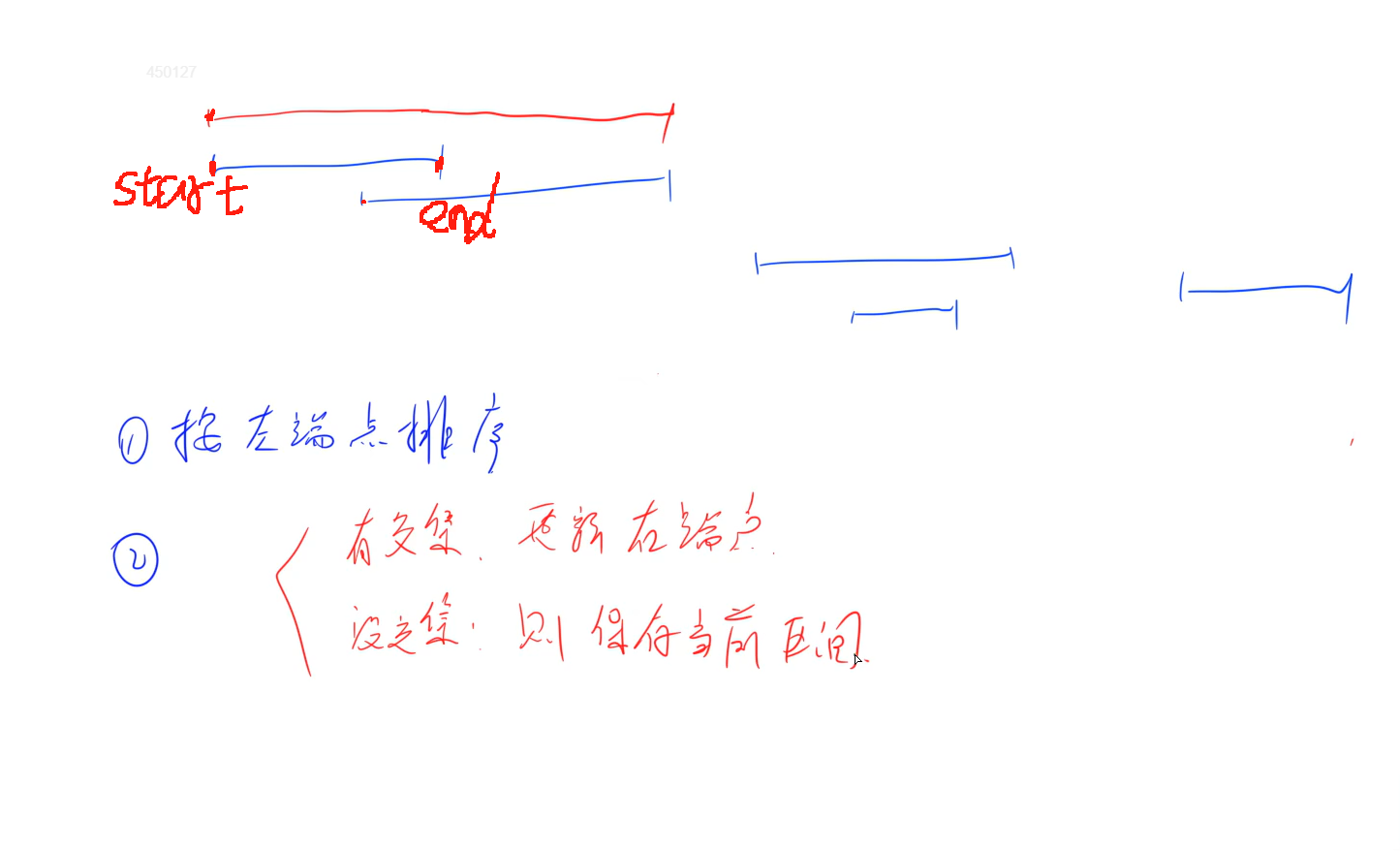
注释代码:
class Solution {public: vector<vector> merge(vector<vector>& a) { vector<vector> res; if(a.empty()) return res; sort(a.begin(), a.end()); //将所有区间按左端点排序,sort会默认按vector的第一个元素的字典序进行排序 int start = a[0][0], end = a[0][1]; for(int i = 0; i end) //如果当前区间的左端点小于之前的区间的右端点,那么合并区间 { res.push_back({start, end}); start = a[i][0], end = a[i][1]; } else{ end = max(end, a[i][1]); //否则更新右端点 } } res.push_back({start, end}); //保存最后一个区间 return res; }};纯享版:
class Solution {public: vector<vector> merge(vector<vector>& a) { vector<vector> res; if(a.empty()) return res; sort(a.begin(), a.end()); int start = a[0][0], end = a[0][1]; for(int i = 0; i end) { res.push_back({start, end}); start = a[i][0], end = a[i][1]; }else{ end = max(end, a[i][1]); } } res.push_back({start, end}); return res; }};LeetCode57.插入区间:
题目描述:
给你一个 无重叠的 ,按照区间起始端点排序的区间列表 intervals,其中 intervals[i] = [starti, endi] 表示第 i 个区间的开始和结束,并且 intervals 按照 starti 升序排列。同样给定一个区间 newInterval = [start, end] 表示另一个区间的开始和结束。
在 intervals 中插入区间 newInterval,使得 intervals 依然按照 starti 升序排列,且区间之间不重叠(如果有必要的话,可以合并区间)。
返回插入之后的 intervals。
注意 你不需要原地修改 intervals。你可以创建一个新数组然后返回它。
示例 1:
输入:intervals = [[1,3],[6,9]], newInterval = [2,5]
输出:[[1,5],[6,9]]
示例 2:
输入:intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出:[[1,2],[3,10],[12,16]]
解释:这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
提示:
0 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= starti <= endi <= 10^5
intervals 根据 starti 按 升序 排列
newInterval.length == 2
0 <= start <= end <= 10^5
思路:
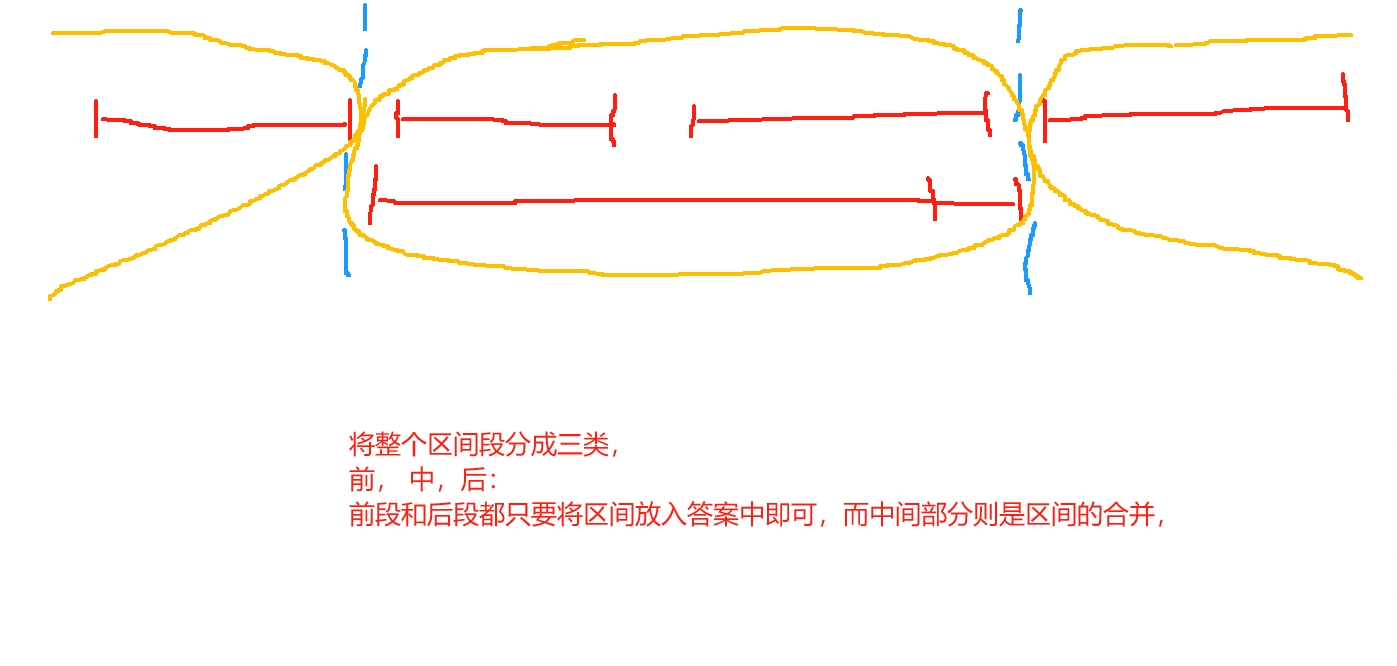
注释代码:
class Solution {public: vector<vector> insert(vector<vector>& a, vector& b) { vector<vector> res; //cout<<b[1]<<endl; int k = 0; while(k < a.size() && a[k][1] < b[0]) res.push_back(a[k++]); //左边没有交集的部分 if(k < a.size()) { //先取小的那端为开头区间端点 b[0] = min(b[0], a[k][0]); while(k < a.size() && a[k][0] <= b[1]) b[1] = max(b[1], a[ k++ ][1]); //比较最后的端点为结尾端点 } res.push_back(b); while(k < a.size()) res.push_back(a[k++]); //右边没有交集的部分 return res; }};纯享版:
class Solution {public: vector<vector> insert(vector<vector>& a, vector& b) { vector<vector> res; int cnt = 0; while(cnt < a.size() && a[cnt][1] < b[0]) res.push_back(a[cnt++]); if(cnt < a.size()) { b[0] = min(b[0], a[cnt][0]); while(cnt < a.size() && a[cnt][0] <= b[1]) b[1] = max(b[1], a[cnt++][1]); } res.push_back(b); while(cnt < a.size()) res.push_back(a[cnt++]); return res; }};LeetCode58.最后一个单词的长度:
题目描述:
给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大
子字符串
。
示例 1:
输入:s = “Hello World”
输出:5
解释:最后一个单词是“World”,长度为 5。
示例 2:
输入:s = \" fly me to the moon \"
输出:4
解释:最后一个单词是“moon”,长度为 4。
示例 3:
输入:s = “luffy is still joyboy”
输出:6
解释:最后一个单词是长度为 6 的“joyboy”。
提示:
1 <= s.length <= 10^4
s 仅有英文字母和空格 ’ ’ 组成
s 中至少存在一个单词
思路:
从后往前,遍历字符串,找到最后一个单词
双指针算法:
注释代码:
class Solution {public: int lengthOfLastWord(string s) { int res = 0; for(int i = s.size() - 1 ; i >= 0; i--) //从后面往前会快一些 { if(s[i] == \' \') continue; //跳过空格 int j = i - 1; //j为i的前一个字符 while(j >= 0 && s[j] != \' \') j--; return i - j; } return 0; }};纯享版:
class Solution {public: int lengthOfLastWord(string s) { for(int i = s.size() - 1; i >= 0; i--) { if(s[i] == \' \') continue; int j = i - 1; while(j >= 0 && s[j] != \' \') j--; return i - j; } return 0; }};语法解法
作为了解:
class Solution {public: int lengthOfLastWord(string s) { stringstream ssin(s); int res = 0; string word; while(ssin >> word) res = word.size(); return res; }};LeetCode59.螺旋矩阵Ⅱ:
题目描述:
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
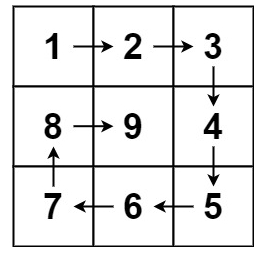
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
1 <= n <= 20
思路:
跟螺旋矩阵一致,还是利用方向数组,这里是要将数填入
代码:
class Solution {public: vector<vector> generateMatrix(int n) { vector<vector> res(n, vector(n)); int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0}; int x = 0, y = 0, d = 0; for(int i = 1; i <= n * n; i++) { res[x][y] = i; int a = x + dx[d], b = y + dy[d]; if(a = n || b = n || res[a][b]) { d = (d + 1) % 4; a = x + dx[d], b = y + dy[d]; } x = a, y = b; } return res; }};LeetCode60.第K个排列:
题目描述:
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
“123”
“132”
“213”
“231”
“312”
“321”
给定 n 和 k,返回第 k 个排列。
示例 1:
输入:n = 3, k = 3
输出:“213”
示例 2:
输入:n = 4, k = 9
输出:“2314”
示例 3:
输入:n = 3, k = 1
输出:“123”
提示:
1 <= n <= 9
1 <= k <= n!
算法1:
时间复杂度:O(n^2)
思路:
排列的题型,大多数都是使用 dfs ,但是求第几个排列,很容易联想到 leetcode31 下一个排列,它利用的思想是,二分结合全排列性质,倒序寻找第一个出现不满足正向倒序的第一个数,然后从这个数后面的数二分找一个比它大的数【不能相等,然后进行交换,然后后面的数进行从大到小排列】。
虽然都是在求有次序的排列,但是本题显然求一个规定的次序,无法借鉴这题。
这题我们从最朴素的枚举思想看 => dfs => 排列类型题为了锁定答案,一般规定字典序排列。
从高位进行枚举,如果第一位选择 1 => 此时,若有 n 位的情况下,应一共有 (n - 1)! 的排列个数,此时如果求的 第 k 个排列的个数大于这个数字,显然,我们应该让第一位枚举下一个数 2。
从这个思想来看,我们的 k 减去 (n - 1)! 的个数。
求第一位选择 2 => 此时仍是 (n - 1)! 的排列数,进一步求已经减去过 (n - 1)! 新的 k 序号是否满足。
以此类推,那么我们就假设枚举的位数为 i ,此时选择一个数在这位,显然应有 (n - 1 - i)! 种可能。
当出现 k <= (n - 1 - i)! 的情况下,说明这位选择的情况下,能覆盖选 第 k 位 的排列,让 i 位锁定这个数字,然后去判断 i + 1 位的数字该选什么数字。
注释代码:
class Solution {public: string getPermutation(int n, int k) { string res; vector st(10); for(int i = 0; i < n; i++) //每个位置的情况 { int fact = 1; for(int j = 1; j <= n - i - 1; j++) fact *= j; //求放完当前位置之后剩余情况 for(int j = 1; j <= n; j++) //从小到大枚举每个数,使顺序最小的尽可能放在前面 { if(!st[j]) //如果没有填过 { if(fact < k) k -= fact; //如果 求的第k种情况大于剩余情况,那么应该是在下一个位置 else{ res += to_string(j); st[j] = true; break; //填过数之后直接跳到下一个位置 } } } } return res; }};纯享版:
class Solution {public: string getPermutation(int n, int k) { string ans; vector st(10); for(int i = 0; i < n; i++) { int fact = 1; for(int j = 1; j <= n - i - 1; j++) fact *= j; for(int j = 1; j <= n; j++) { if(!st[j]) { if(fact < k) k -= fact; else{ ans += to_string(j); st[j] = true; break; } } } } return ans; }};语法做法:
时间复杂度:O(nk)
class Solution {public: string getPermutation(int n, int k) { string res; for(int i = 1; i <= n; i++) { res += to_string(i); } for(int i = 0; i < k - 1; i++) { next_permutation(res.begin(), res.end()); } return res; }};LeetCode61.旋转链表:
题目描述:
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
示例 1:
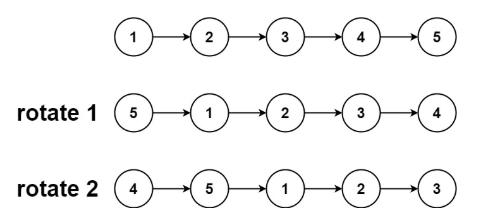
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
示例 2:
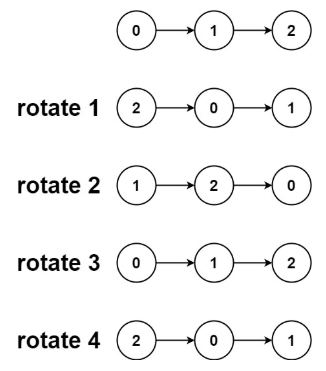
输入:head = [0,1,2], k = 4
输出:[2,0,1]
提示:
链表中节点的数目在范围 [0, 500] 内
-100 <= Node.val <= 100
0 <= k <= 2 * 10^9
思路:
这种重复一种操作一直循环的题先不要着急怎么写,先分析它的循环规律,找到循环的关键点,比如这题:从示例2中可以看出当K超过链表的长度时,又会重新回到原点之后小于链表长度的某一步,于是我们可以求出链表长度,再让k模于n(链表长度)这样不管k多大最终旋转的次数也只是在链表长度之内,同时,在链表长度内旋转就是将后面的k个节点搬到最前面重新拼接链表,如图:
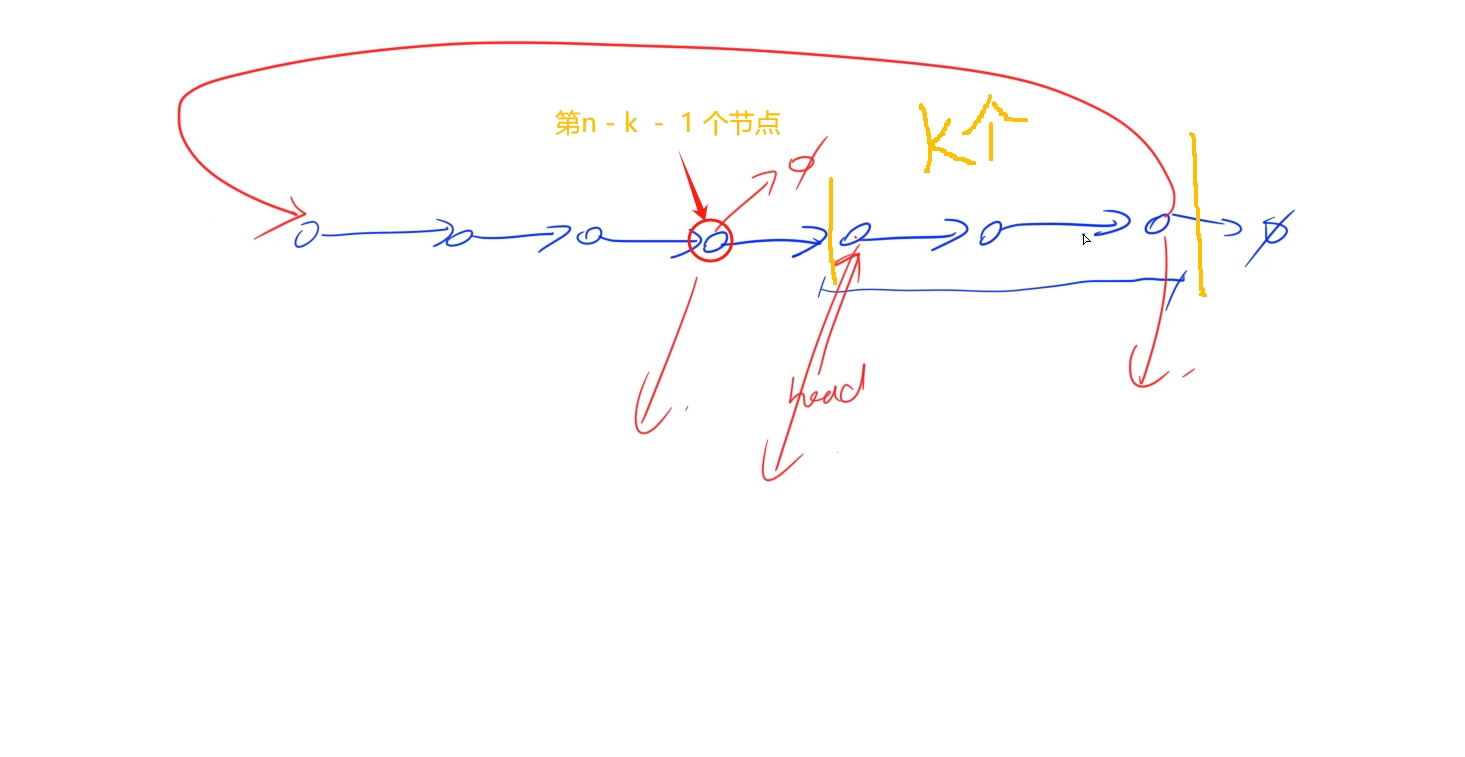
代码要点:
#.求链表长度
#.找到需要改变连接的三个节点: tail(原本的尾节点,新链表中要连接到原来的头节点之上) , 第n - k - 1 个节点(新的最末尾的节点),以及它后面的节点(新的头节点)
#.改变连接节点之间的连接,注意不要发生覆盖丢失
注释代码:
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */class Solution {public: ListNode* rotateRight(ListNode* head, int k) { if(!head) return head; int n = 0; ListNode* tail; for(auto p = head; p; p = p -> next) { tail = p; //记录尾节点 n++; //记录链表的长度 } k %= n; //将k的重复旋转滤除 if(!k) return head; auto start = head; for(int i = 0; i next; //找到第n - k - 1个节点 } tail -> next = head; //将尾节点连接到开头 head = start -> next; //更新头节点 start -> next = NULL; //设定尾节点 return head; }};纯享版:
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */class Solution {public: ListNode* rotateRight(ListNode* head, int k) { if(!head) return head; int n = 0; ListNode* tail; for(auto p = head; p; p = p -> next) { tail = p; n++; } k %= n; //cout<<k<<endl; if(!k) return head; auto p = head; for(int i = 0; i next; tail -> next = head; head = p -> next; p -> next = NULL; return head; }};LeetCode62.不同路径:
题目描述:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
思路:
动态规划问题: 设定集合f[i,j]: 表示从起点到(i , j)的方案数之和

时间复杂度:O(n * m) : 每个格子会遍历一次
空间复杂度:O(n * m) : 每个格子的状态会存储下来
注释代码:
class Solution {public: int uniquePaths(int m, int n) { vector<vector> f(n, vector(m)); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { if(!i && !j) f[i][j] = 1; //起点只有一种方案 else{ if(i) f[i][j] += f[i - 1][j]; //i不为0说明能从上面走下来 if(j) f[i][j] += f[i][j - 1]; //j不为0说明能从左边走过来 } } } return f[n - 1][m - 1]; }};纯享版:
class Solution {public: int uniquePaths(int m, int n) { vector<vector> f(n, vector(m)); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { if(!i && !j) f[i][j] = 1; else{ if(i) f[i][j] += f[i - 1][j]; if(j) f[i][j] += f[i][j - 1]; } } } return f[n - 1][m - 1]; }};LeetCode63.不同路径Ⅱ:
题目描述:
给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角(即 grid[0][0])。机器人尝试移动到 右下角(即 grid[m - 1][n - 1])。机器人每次只能向下或者向右移动一步。
网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。
返回机器人能够到达右下角的不同路径数量。
测试用例保证答案小于等于 2 * 10^9。
示例 1:
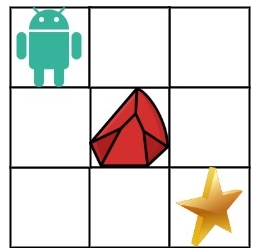
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
思路:
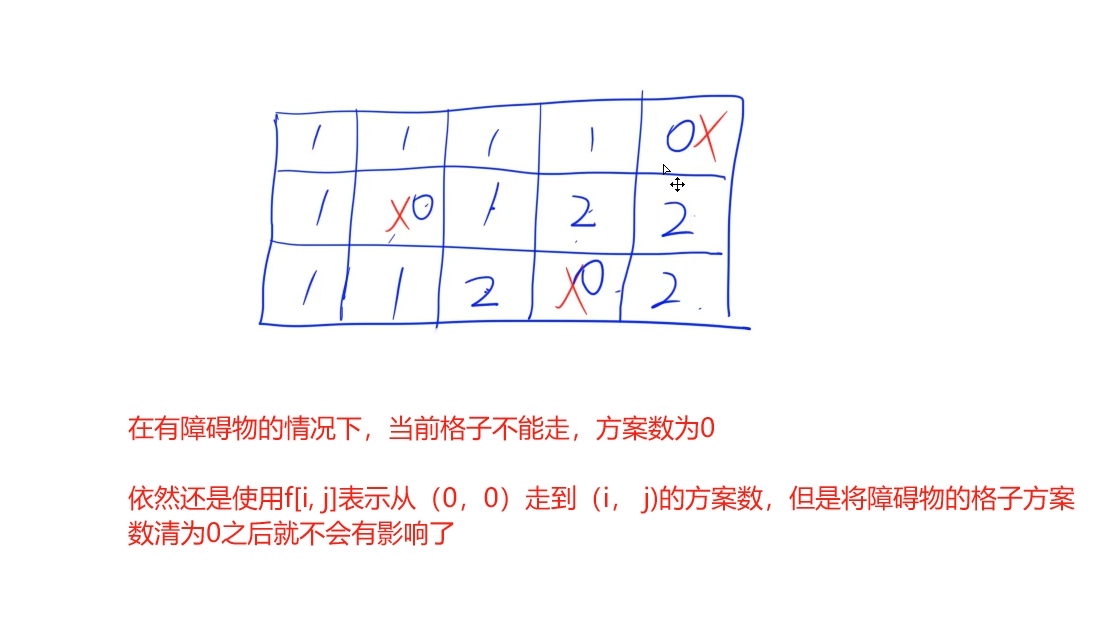
时间复杂度:O(n * m) : 遍历每个格子看是否能走并且更新状态
空间复杂度:O(n * m) : 存储每个格子的路径方案数
注释代码:
class Solution {public: int uniquePathsWithObstacles(vector<vector>& o) { int n = o.size(); if(!n) return 0; int m = o[0].size(); vector<vector> f(n, vector(m)); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { if(!o[i][j]) //如果当前位置能走,则才有方案数 { if(!i && !j) f[i][j] = 1; else{ if(i) f[i][j] += f[i - 1][j]; if(j) f[i][j] += f[i][j - 1]; } } } } return f[n - 1][m - 1]; }};纯享版:
class Solution {public: int uniquePathsWithObstacles(vector<vector>& a) { int n = a.size(); if(!n) return 0; int m= a[0].size(); vector<vector> f(n, vector(m)); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { if(!a[i][j]) { if(!i && !j) f[i][j] = 1; else{ if(i) f[i][j] += f[i - 1][j]; if(j) f[i][j] += f[i][j - 1]; } } } } return f[n - 1][m - 1]; }};LeetCode64.最小路径和:
题目描述:
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
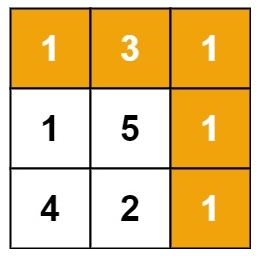
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200
思路:
动态规划:设定集合f[i,j]表示从起点到(i,j)最小的路径和
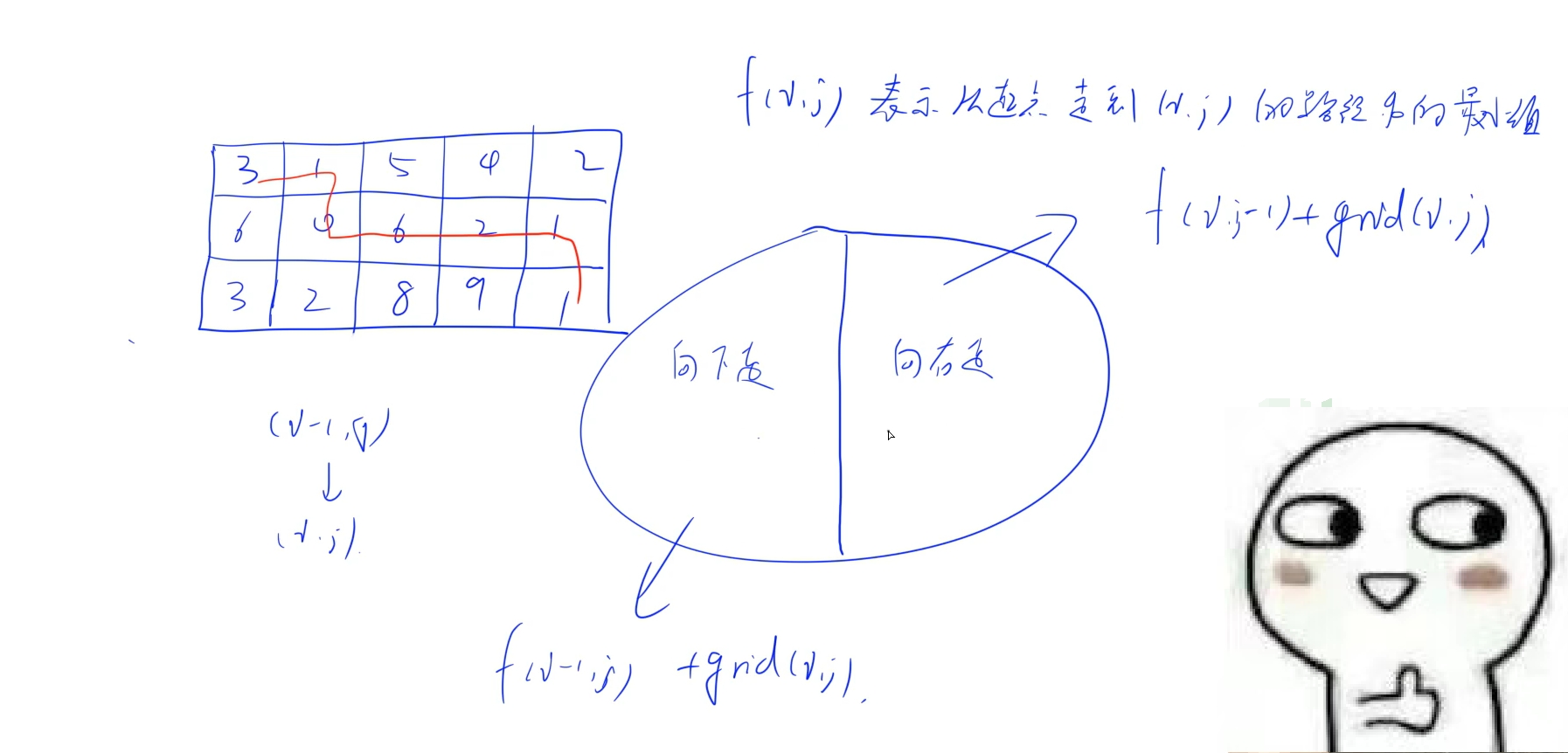
时间复杂度:O(n * m) : 遍历每个格子
空间复杂度:O(n * m) :存储每个格子上路径最小值
注释代码:
class Solution {public: int minPathSum(vector<vector>& grid) { int n = grid.size(); if(!n) return 0; int m = grid[0].size(); vector<vector> f(n, vector(m, INT_MAX)); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { if(!i && !j) f[i][j] = grid[i][j]; //起点的最小路径是本身 else{ if(i) f[i][j] = min(f[i][j], f[i - 1][j] + grid[i][j]); //从上方下来的最小路径 if(j) f[i][j] = min(f[i][j], f[i][j - 1] + grid[i][j]); //从左方过来的最小路径 } } } return f[n - 1][m - 1]; }};纯享版:
class Solution {public: int minPathSum(vector<vector>& grid) { int n= grid.size(); if(!n) return 0; int m = grid[0].size(); vector<vector> f(n, vector(m, INT_MAX)); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { if(!i && !j) f[i][j] = grid[i][j]; else{ if(i) f[i][j] = min(f[i][j], f[i - 1][j] + grid[i][j]); if(j) f[i][j] = min(f[i][j], f[i][j - 1] + grid[i][j]); } } } return f[n - 1][m - 1]; }};LeetCode65.有效数字:
题目描述:
给定一个字符串 s ,返回 s 是否是一个 有效数字。
例如,下面的都是有效数字:“2”, “0089”, “-0.1”, “+3.14”, “4.”, “-.9”, “2e10”, “-90E3”, “3e+7”, “+6e-1”, “53.5e93”, “-123.456e789”,而接下来的不是:“abc”, “1a”, “1e”, “e3”, “99e2.5”, “–6”, “-+3”, “95a54e53”。
一般的,一个 有效数字 可以用以下的规则之一定义:
一个 整数 后面跟着一个 可选指数。
一个 十进制数 后面跟着一个 可选指数。
一个 整数 定义为一个 可选符号 ‘-’ 或 ‘+’ 后面跟着 数字。
一个 十进制数 定义为一个 可选符号 ‘-’ 或 ‘+’ 后面跟着下述规则:
数字 后跟着一个 小数点 .。
数字 后跟着一个 小数点 . 再跟着 数位。
一个 小数点 . 后跟着 数位。
指数 定义为指数符号 ‘e’ 或 ‘E’,后面跟着一个 整数。
数字 定义为一个或多个数位。
示例 1:
输入:s = “0”
输出:true
示例 2:
输入:s = “e”
输出:false
示例 3:
输入:s = “.”
输出:false
提示:
1 <= s.length <= 20
s 仅含英文字母(大写和小写),数字(0-9),加号 ‘+’ ,减号 ‘-’ ,或者点 ‘.’ 。
思路:
面向数据编程!
注释代码:
class Solution {public: bool isNumber(string s) { //1.前后空格 int l = 0, r = s.size() - 1; while(l <= r && s[l] == \' \') l++; while(l <= r && s[r] == \' \') r--; if(r < l) return false; s.substr(l, r - 1 + 1); //将没有空格的一段截取出来 //2.正负号先拿出来,不能出现单独符号 if(s[0] == \'+\' || s[0] == \'-\') s = s.substr(1); if(s.empty()) return false; //3. \'.\' 不能单独出现,也不能出现在e和E的前面 if(s[0] == \'.\' && (s.size() == 1 || s[1] == \'e\' || s[1] == \'E\')) return false; //4. \'.\'和\'e\'只能出现一次 int dot = 0, e = 0; for(int i = 0; i 0 || e > 0) return false; dot++; }else if(s[i] == \'e\' || s[i] == \'E\') { //e/E的前面和后面不能为空 if(!i || i + 1 == s.size() || e > 0) return false; //e/E的后面可以为正负号,但是符号后面不能为空 if(s[i + 1] == \'+\' || s[i + 1] == \'-\'){ if(i + 2 == s.size()) return false; i++; } e++; }else if(s[i] \'9\') return false; } return true; }};纯享版:
class Solution {public: bool isNumber(string s) { //1.去除空格 int l = 0, r = s.size() - 1; while(l <= r && s[l] == \' \') l++; while(l <= r && s[r] == \' \') r--; //cout<<s<<endl; if(r < l) return false; s.substr(l, r - l + 1); //2.将符号拿出来 if(s[0] == \'+\' || s[0] == \'-\') s = s.substr(1); cout<<s<<endl; if(s.empty()) return false; cout<<s<<endl; //3. \'.\' \'E\' \'e\' 不能单独出现 if(s[0] == \'.\' && (s.size() == 1 || s[1] == \'e\' || s[1] == \'E\')) return false; cout<<s<<endl; //4. int dot = 0, e = 0; for(int i = 0; i 0 || e > 0) return false; dot++; }else if(s[i] == \'e\' || s[i] == \'E\') { if(!i || i + 1 == s.size() || e > 0) return false; if(s[i + 1] == \'+\' || s[i + 1] == \'-\') { if(i + 2 == s.size()) return false; i++; } e++; }else if(s[i] \'9\') return false; } return true; }};LeetCode66.加一:
题目描述:
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
示例 2:
输入:digits = [4,3,2,1]
输出:[4,3,2,2]
解释:输入数组表示数字 4321。
示例 3:
输入:digits = [9]
输出:[1,0]
解释:输入数组表示数字 9。
加 1 得到了 9 + 1 = 10。
因此,结果应该是 [1,0]。
提示:
1 <= digits.length <= 100
0 <= digits[i] <= 9
思路:高精度加法,算法基础课复习!
时间复杂度: O(n)
注释代码:
class Solution {public: vector plusOne(vector& digits) { //数字颠倒: reverse(digits.begin(), digits.end()); //数字进位 int t = 1; for(int i = 0; i < digits.size(); i++) { t += digits[i]; digits[i] = t % 10; t /= 10; } //多出的一位将它插回数组 if(t) digits.push_back(t); //翻转回来 reverse(digits.begin(), digits.end()); return digits; }};纯享版:
class Solution {public: vector plusOne(vector& digits) { reverse(digits.begin(), digits.end()); int t = 1; for(auto& x : digits) { t += x; x = t % 10; t /= 10; } if(t) digits.push_back(t); reverse(digits.begin(), digits.end()); return digits; }};LeetCode67.二进制求和:
题目描述:
给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。
示例 1:
输入:a = “11”, b = “1”
输出:“100”
示例 2:
输入:a = “1010”, b = “1011”
输出:“10101”
提示:
1 <= a.length, b.length <= 10^4
a 和 b 仅由字符 ‘0’ 或 ‘1’ 组成
字符串如果不是 “0” ,就不含前导零
思路:高进度加法!
时间复杂度:O(max(n, m))
注释代码:
class Solution {public: string addBinary(string a, string b) { reverse(a.begin(), a.end()); reverse(b.begin(), b.end()); string c; for(int i = 0, t = 0; i < a.size() || i < b.size() || t; i++) { if(i < a.size()) t += a[i] - \'0\'; if(i < b.size()) t += b[i] - \'0\'; cout<<t<<endl; c += to_string(t % 2); t /= 2; } reverse(c.begin(), c.end()); return c; }};纯享版:
class Solution {public: string addBinary(string a, string b) { reverse(a.begin(), a.end()); reverse(b.begin(), b.end()); int t = 0; string c; for(int i = 0; i < a.size() || i < b.size() || t; i++) { if(i < a.size()) t += a[i] - \'0\'; if(i < b.size()) t += b[i] - \'0\'; c += to_string(t % 2); t /= 2; } reverse(c.begin(), c.end()); return c; }};LeetCode68.文本左右对齐:
题目描述:
给定一个单词数组 words 和一个长度 maxWidth ,重新排版单词,使其成为每行恰好有 maxWidth 个字符,且左右两端对齐的文本。
你应该使用 “贪心算法” 来放置给定的单词;也就是说,尽可能多地往每行中放置单词。必要时可用空格 ’ ’ 填充,使得每行恰好有 maxWidth 个字符。
要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配,则左侧放置的空格数要多于右侧的空格数。
文本的最后一行应为左对齐,且单词之间不插入额外的空格。
注意:
单词是指由非空格字符组成的字符序列。
每个单词的长度大于 0,小于等于 maxWidth。
输入单词数组 words 至少包含一个单词。
示例 1:
输入: words = [“This”, “is”, “an”, “example”, “of”, “text”, “justification.”], maxWidth = 16
输出:
[
“This is an”,
“example of text”,
\"justification. \"
]
示例 2:
输入:words = [“What”,“must”,“be”,“acknowledgment”,“shall”,“be”], maxWidth = 16
输出:
[
“What must be”,
\"acknowledgment \",
\"shall be \"
]
解释: 注意最后一行的格式应为 \"shall be \" 而不是 “shall be”,
因为最后一行应为左对齐,而不是左右两端对齐。
第二行同样为左对齐,这是因为这行只包含一个单词。
示例 3:
输入:words = [“Science”,“is”,“what”,“we”,“understand”,“well”,“enough”,“to”,“explain”,“to”,“a”,“computer.”,“Art”,“is”,“everything”,“else”,“we”,“do”],maxWidth = 20
输出:
[
“Science is what we”,
“understand well”,
“enough to explain to”,
“a computer. Art is”,
“everything else we”,
\"do \"
]
提示:
1 <= words.length <= 300
1 <= words[i].length <= 20
words[i] 由小写英文字母和符号组成
1 <= maxWidth <= 100
words[i].length <= maxWidth
思路:双指针:
核心步骤
1、先计算出当前行最多能放多少个单词,每个单词之间最少用一个空格隔开(通过双指针计算能放单词的总长度len)
2、假设当前行最多能放x个单词,需要满足下面3个条件进行放置
1、如果当前行是最后一行,则向左对齐(后面多余的用空格补上)
2、如果当前行只有一个单词,则向左对齐(后面多余的用空格补上)
3、其他情况均左右对齐
左右对齐的情况
在当前行中,通过i和j的位置可以知道一共有j - i个单词,因此有cnt = j - i - 1个空隙,len - cnt表示的是 单词占的长度 = 能放的单词总长度 - 空隙数,
例如The is a apple,长度是14,空隙数是3,因此res = maxWidth - (len - cnt)表示的是当前行的总空格数,a = res / cnt表示每个空隙的空格数基础是a,多余b = res % cnt个空格数,多余的需要平均分配给前面的空隙,
例如res = 15,cnt = 4,则空隙数是4,基础空格数是3,多余是3,因此每个空隙的基础空格数是3 3 3 3,补上多余的就是4 4 4 3,
注意:用StringBuffer会加快执行速度
时间复杂度:O(n)
注释代码:
class Solution {public: vector fullJustify(vector& words, int maxWidth) { vector res; for(int i = 0; i < words.size(); i++) //枚举每个单词 { int j = i + 1; //看下一个单词 int len = words[i].size(); //判断能塞几个单词(当前行的最后的单词位置) while(j < words.size() && len + 1 + words[j].size() <= maxWidth) { len += 1 + words[j].size(); j++; } string line; //如果可以跳到最后一个单词(说明该行是最后一行)或者这行只能放一个单词 if(j == words.size() || j == i + 1) //左对齐 { line += words[i]; for(int k = i + 1; k < j; k++) line += \' \' + words[k]; while(line.size() < maxWidth) line += \' \'; //长度不足在后面补空格 }else{ //左右对齐 int cnt = j - i - 1; //看这行放了几个单词 int r = maxWidth - len + cnt; //剩余的位置(除去空格之后) line += words[i]; int k = 0; while(k < r % cnt) //给前 r / cnt 个单词分配多余空格 { line += string(r / cnt + 1, \' \') + words[i + k + 1]; k++; } while(k < cnt) //后面的则按正常分配 { line += string(r / cnt, \' \') + words[i + k + 1]; k++; } } res.push_back(line); i = j - 1; //当前行放完了,下一行的单词起始位置为j - 1 } return res; }};纯享版:
class Solution {public: vector fullJustify(vector& words, int maxWidth) { vector res; for(int i = 0; i < words.size(); i++) { int j = i + 1; int len = words[i].size(); while(j < words.size() && len + 1 + words[j].size() <= maxWidth) { len += words[j].size() + 1; j++; } string line; if(j == words.size() || j == i + 1) //左对齐 { line += words[i]; for(int k = i + 1; k < j; k++) line += \' \' + words[k]; while(line.size() < maxWidth) line += \' \'; }else{ int cnt = j - i - 1; int r = maxWidth - len + cnt; int k = 0; line += words[i]; while(k < r % cnt) { line += string(r / cnt + 1, \' \') + words[i + k + 1]; k++; } while(k < cnt) { line += string(r / cnt, \' \') + words[i + k + 1]; k++; } } res.push_back(line); i = j - 1; } return res; }};LeetCode69.X的平方根:
题目描述:
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 2^31 - 1
思路:
充分理解二分思想,这里x开方的开方数一定小于x,那么我们就需要在0~x中找到 mid * mid <= x 的最后一个mid,而二分的思想就是找到最后的边界位置,于是选择前段区间为我们的check条件:
if(check(mid) <= x) l = mid; else r = mid - 1;
注释代码:
class Solution {public: int mySqrt(int x) { int l = 0, r = x; while(l > 1; //l + r + 1 可能会超出int范围,使用使用long long if(mid <= x / mid) l = mid; //mid * mid 可能会超出int范围,所以使用除法 else r = mid - 1; } return r; }};纯享版:
class Solution {public: int mySqrt(int x) { int l = 0, r = x; while(l > 1; if(mid <= x / mid) l = mid; else r = mid - 1; } return r; }};LeetCode70.爬楼梯:
题目描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
提示:
1 <= n <= 45
思路:
动态规划思想: 当前台阶由前两节台阶的方案数组成(因为一次能走两步或者一步) 为了节省空间只需要设置三个变量a, b, c就可以维持从前往后的台阶的方案数

注释代码:
class Solution {public: int climbStairs(int n) { int a = 1, b = 1; //位于第0阶台阶和第一阶都只有一种方案 while(--n) { int c = a + b; a = b; b = c; } return b; //b为第n项 }};纯享版:
class Solution {public: int climbStairs(int n) { int a = 1, b = 1; while(--n) { int c = a + b; a = b; b = c; } return b; }};

