【图论基础】Bellman-Ford 算法：负权图的最短路径利器_负权图最短路径例题

• 🎓作者简介：CS专业的大一在校生
• 👨‍💻 博主主页：@Ahu_iii
• 📚 所属专栏：《基础算法》

---

1. 算法原理

Bellman-Ford 算法是用于单源最短路径的一种经典算法，不同于Dijkstra，该算法适用于边权可能为负的图。

核心思想：不断”松弛“。

松弛（Relaxation）：不断尝试通过一条边更新路径长度，若能更优则更新。
负环：若第 $n$ 次依旧能够进行松弛，说明存在负权环（负环）。

原理解释

松弛操作就像是将一条连接两端点的”紧绷“的尺子，通过不断插入新的尺子使得尺子间形成的”路线“越来越”松“。在存在 $n$ 个结点的图中，最多可形成包含 $n-1$ 条边的一条路径（如果没有环）。
负环检测机制的原理在于，当我们第 $n$ 次尝试松弛时，此时若还能够松弛，意味着存在环并且为负权环使得能够通过继续且不断地”加边“来缩短路径距离。

为什么Dijkstra无法处理负权图？
Dijkstra 是基于贪心策略的算法，一旦访问某点就不再更新，也就是说若后续出现能够使路径再度缩短的负权边时，不会”回头“更新。

与Dijkstra对比

特性 Dijkstra Bellman-Ford 处理负权边 不可处理 可处理 复杂度 $O(m\log n)$ (堆优化) $O(nm)$ 思想 贪心 + 堆 动态规划式松弛 数据结构 优先队列 简单数组遍历

适用范围

特性 Bellman-Ford 有向图 / 无向图 Yes 含负权边 Yes 检测负环 Yes 稀疏图 Yes 稠密图 不推荐（效率不高）

2. 算法流程演示

为了更直观地看到最短路是如何被松弛出的，这里用一个小小的有向图来演示算法是如何工作的。

步骤 松弛边 距离变化 (A,B,C,D) 说明 初始 - [0, ∞, ∞, ∞] 起点 A 初始化为 0 第1轮 A→B [0, 4, ∞, ∞] B 从 ∞ 更新为 0+4=4 A→C [0, 4, 5, ∞] C 从 ∞ 更新为 0+5=5 B→C [0, 4, 2, ∞] B(4)+(-2)=2 < 5，更新 C C→D [0, 4, 2, 5] C(2)+3=5，更新 D D→B [0, 1, 2, 5] D(5)+(-4)=1 < B(4)，更新 B 第2轮 B→C [0, 1, -1, 5] B(1)+(-2)=-1 < C(2)，更新 C C→D [0, 1, -1, 2] C(-1)+3=2 < D(5)，更新 D D→B [0, -2, -1, 2] D(2)+(-4)=-2 < B(1)，更新 B 第3轮 B→C [0, -2, -4, 2] B(-2)+(-2)=-4 < C(-1)，更新 C C→D [0, -2, -4, -1] C(-4)+3=-1 < D(2)，更新 D D→B [0, -5, -4, -1] D(-1)+(-4)=-5 < B(-2)，更新 B 检测环 B→C -5+(-2) = -7 < C(-4) 检测到负权环

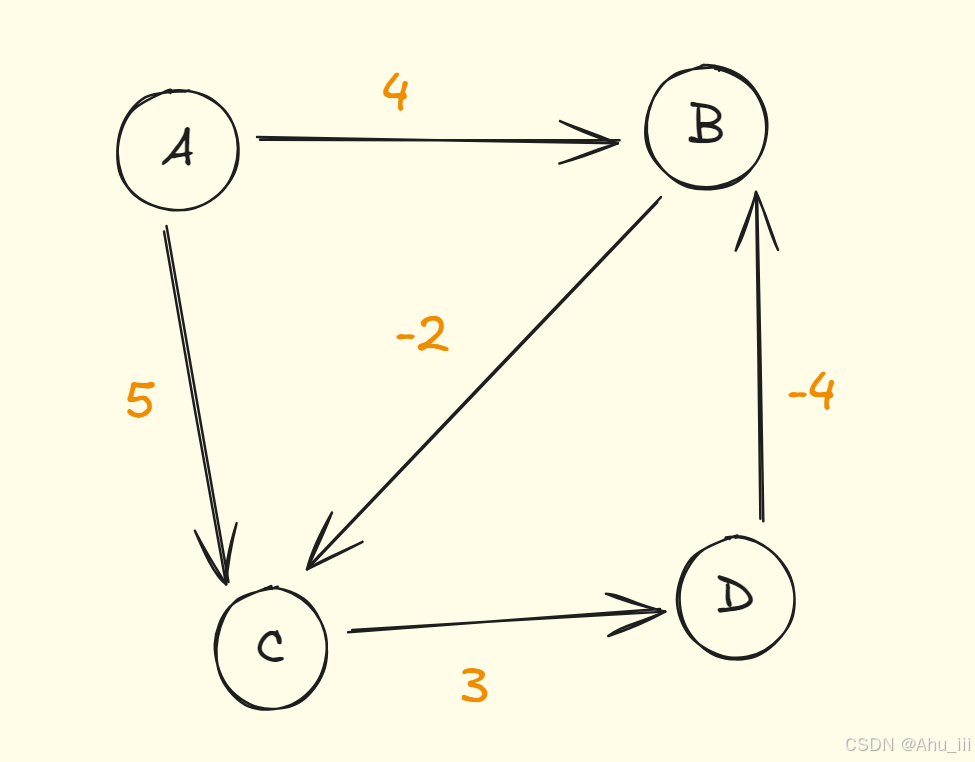
3. 算法模板

实现步骤

1. 初始化：设源点距离为0，其他点为无穷大
2. 重复 $n-1$ 次松弛操作
3. 第 $n$ 次检查是否还能松弛（负环检测）

const int INF = 1e9;int n, m;int dist[N];struct Edge {int u, v, w;}edges[N];bool bellman_ford(int s) { for (int i = 1; i <= n; ++i) dist[i] = INF; dist[s] = 0; for (int i = 1; i <= n; ++i) { bool updated = false; for (int j = 0; j < m; ++j) { int u = edges[j].u, v = edges[j].v, w = edges[j].w; if (dist[u] < INF && dist[v] > dist[u] + w) { dist[v] = dist[u] + w; updated = true; if (i == n) return true; //若第 n 次依旧松弛，存在负环 } } if (!updated) break;//不能松弛，提前结束 } return false;}

存在两层循环，外层循环 $n$ 次，内层循环 $m$ 次，且所用空间取决于结点数和边数。
时间复杂度： $O(nm)$
空间复杂度：$O(n+m)$

⚠️注意：确定图中无负环时才能提前终止循环，否则可能会导致无法判出负环。

3. 实际例题

洛谷 P3385 【模板】负环

题目描述

给定一个 $n$ 个点的有向图，请求出图中是否存在从顶点 $1$ 出发能到达的负环。

负环的定义是：一条边权之和为负数的回路。

输入格式

本题单测试点有多组测试数据。

输入的第一行是一个整数 $T$，表示测试数据的组数。对于每组数据的格式如下：

第一行有两个整数，分别表示图的点数 $n$ 和接下来给出边信息的条数 $m$。

接下来 $m$ 行，每行三个整数 $u,v,w$。

• 若 $w\ge 0$，则表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边，还存在一条从 $v$ 至 $u$ 边权为 $w$ 的边。
• 若 $w<0$，则只表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边。

输出格式

对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

输入样例

23 41 2 21 3 42 3 13 1 -33 31 2 32 3 43 1 -8

输出样例

NOYES

说明/提示

数据规模与约定

对于全部的测试点，保证：

• 1 ≤ n ≤ 2 × 1 0 3 1 \\leq n \\leq 2 \\times 10^3 1≤n≤2×103， 1 ≤ m ≤ 3 × 1 0 3 1 \\leq m \\leq 3 \\times 10^3 1≤m≤3×103。
• $1\le u,v\le n$， − 1 0 4 ≤ w ≤ 1 0 4 -10^4 \\leq w \\leq 10^4 −104≤w≤104。
• $1\le T\le 10$。

提示

请注意，$m$ 不是图的边数。

题目分析：

题目要求我们判断是否存在从起点 1 出发的负权环，满足可用于负环检测的单源最短路径Bellman-Ford算法。

注意事项：

1. 多组数据 ：每组需清空edge，重置 dist；
2. 双向边构造：仅在 $w\ge 0$ 时添加反向边；
3. 判负环：在第 $n$ 轮继续松弛成功时说明存在负环；
4. 可达限制 ： 判断时需 dist[u] < INF；

具体实现：

#include #include using namespace std;const int INF = 1e9;struct Edge { int u, v, w;}edges[10005];//尽量开大int dist[2005]; //2 * 1e3int T, n, m, cnt; //cnt存放边数bool bellman_ford(int start) { fill(dist + 1, dist + n + 1, INF); dist[start] = 0; for (int i = 1; i <= n; i++) { bool updated = false; for (int j = 0; j < cnt; j++) { int u = edges[j].u, v = edges[j].v, w = edges[j].w; if (dist[u] < INF && dist[v] > dist[u] + w) { dist[v] = dist[u] + w; updated = true; if (i == n) return true; } } if (!updated) break; } return false;}void add_edge(int u, int v, int w) { //建边 edges[cnt].u = u; edges[cnt].v = v; edges[cnt++].w = w;}int main() { ios::sync_with_stdio(false); cin.tie(nullptr); cin >> T; while (T--) { for (int i = 0; i < cnt; i++) { edges[i].u = edges[i].v = edges[i].w = 0; //置空并重置边数 } cnt = 0; cin >> n >> m; for (int i = 0; i < m; i++) { int u, v, w; cin >> u >> v >> w; add_edge(u, v, w); if (w >= 0) add_edge(v, u, w);//权值为正是双向边 } cout << (bellman_ford(1) ? \"YES\\n\" : \"NO\\n\"); } return 0;}