力扣 路径总合题目总结（1，2，3）

路径总和1
路径总和2
路径总和3

路径总和1 题目：

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

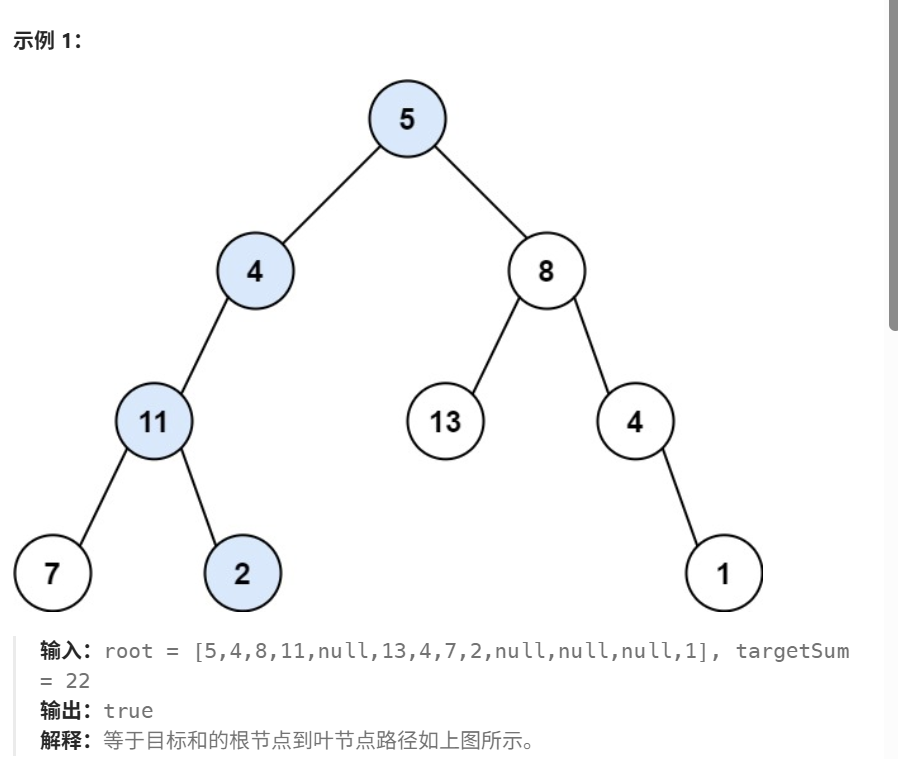
分析：

最基础的二叉树路径问题，这里求的是是否包含这样一条路径，如果包含则返回true，否则返回false。在写二叉树递归模板的时候，经常会分不清递归需不需要返回值。其实可以根据题目来判断，通常如果需要将整颗二叉树遍历，那么此时递归一般不需要返回值，每层递归的处理结果都放在一个公共全局变量中处理，这样每层递归也不需要传入这个参数，更加清晰。如果不需要遍历整棵树，比如像这一题，只要发现存在路径就return true。这种往往需要递归返回值，递归返回值作用是来控制是否进入下一层递归。具体看代码：
这里判断路径长度是否满足，用减法判断是否等于0，而不是累加判断，这样也是个小技巧。这样代码比较简单

//进入递归public boolean hasPathSum(TreeNode root, int targetSum) { if(root==null){ return false; }  return travel(root,targetSum-root.val); }

//递归主体public boolean travel(TreeNode root,int count){//递归结束条件：到叶子节点，此时根据路径长度是否//满足要求给出返回值 if(root.left==null&&root.right==null){ if(count==0){ return true; }else { return false; } } if(root.left!=null){ //这里有两点注意： //1.根据上层递归的返回值判断，如果是true，说明找到 //符合要求路径，也返回true，否则返回false //2.传入下一层递归的参数count-root.left.val，这里 //有回溯的处理，这样传参，返回上一层递归的时候count数值 //没有改变，可以直接回溯。否则需要这样处理： //if (cur->left) { // 左 // count -= cur->left->val; // 递归，处理节点; // if (traversal(cur->left, count)) return true; // count += cur->left->val; // 回溯，撤销处理结果// } if(travel(root.left,count-root.left.val)){ return true; } } if(root.right!=null){ if(travel(root.right,count-root.right.val)){ return true; } } return false; }

路径总和2 题目：

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

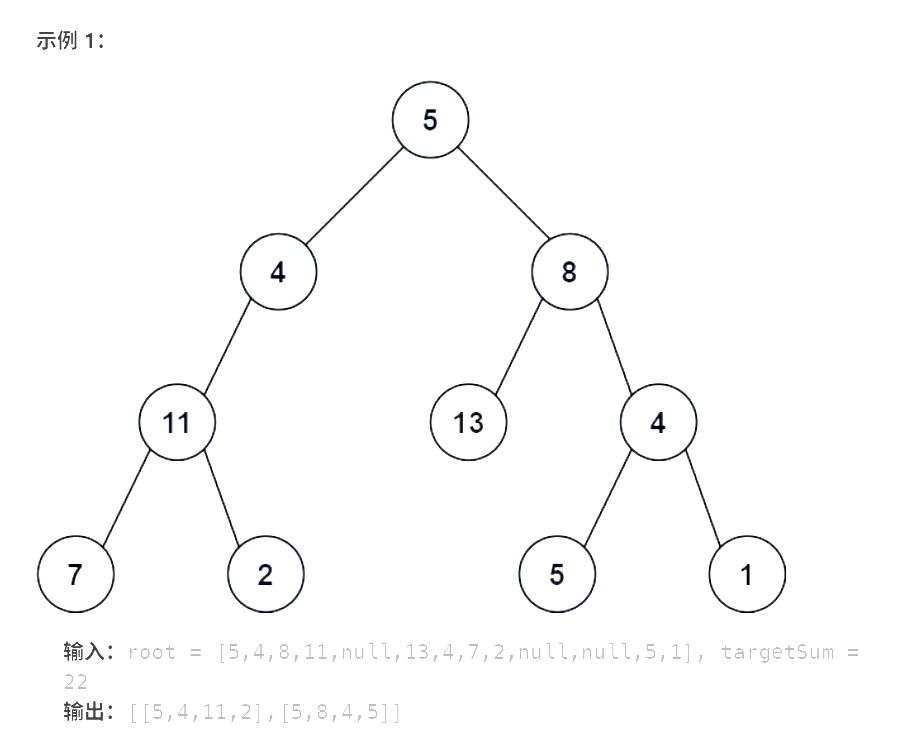
分析：

路径总和 2 和路径总和1不同点在于，这里最后题目要求返回是一个集合，集合里面是满足条件的路径。这就要求必须要遍历完整棵树，所以递归条件不含返回值。另外这里用全局变量path存储遍历路径，每次递归回溯都对path进行处理，如果满足条件直接把path加入集合

class Solution { List<List<Integer>> result=new ArrayList<>(); List<Integer> path =new ArrayList<>(); public List<List<Integer>> pathSum(TreeNode root, int targetSum) { if(root==null){ return result; } path.add(root.val); travel(root,targetSum-root.val,path); return result; }//没有返回值，处理都在path变量中 public void travel(TreeNode root,int count,List path){ if(root.left==null&&root.right==null){ if(count==0){ result.add(new ArrayList<>(path)); } return; } if(root.left!=null){ path.add(root.left.val); travel(root.left,count-root.left.val,path); path.remove(path.size()-1); } if(root.right!=null){ path.add(root.right.val); travel(root.right,count-root.right.val,path); path.remove(path.size()-1); } }}

路径总和3 题目：

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

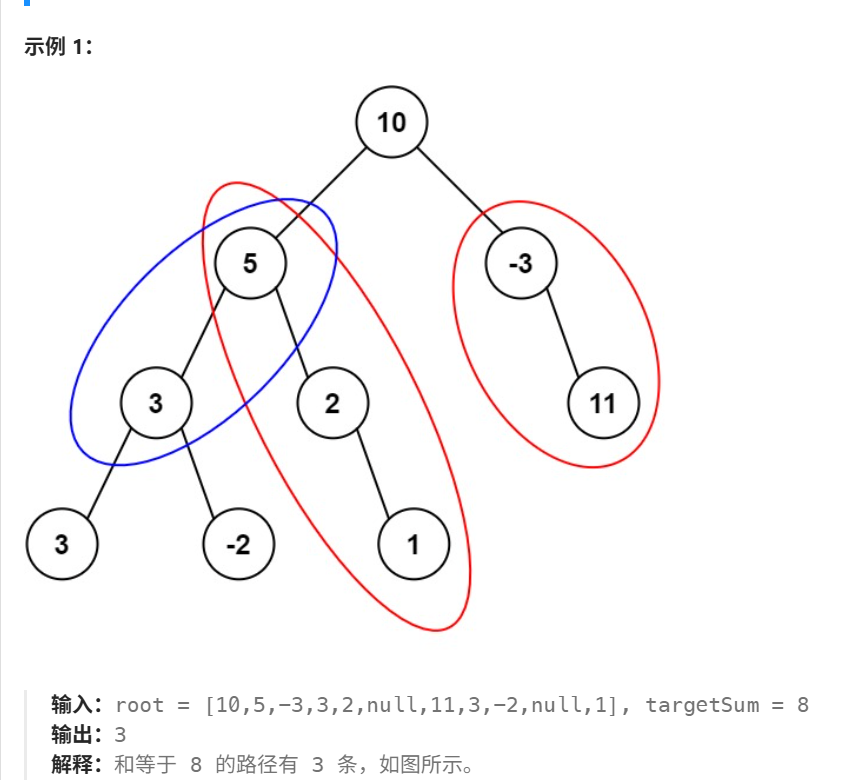
分析：

这题在路径总和2基础上有了扩展，这里的路径有了新的定义，起点和终点不需要是根节点和叶子节点。只要从上向下就行。这里返回的是满足路径1条数，所以仍需要遍历整棵树，递归函数不需要返回值。这里用两个递归来实现，一个递归用来处理是否满足长度的路径，大体和题目2相同，只有一些细节差异。另一个递归用来前序遍历整棵树，因为根节点不确定性，所以前序遍历，让每个节点都作为路径的初始节点。

class Solution { int ans=0; public int pathSum(TreeNode root, int targetSum) { if(root==null){ return ans; } travel1(root,targetSum); return ans; } public void travel1(TreeNode root,long targetSum1){ if(root==null){ return; } //每个节点递归判断，是否能满足情况 travel2(root,targetSum1); if(root.left!=null){ travel1(root.left, targetSum1); } if(root.right!=null){ travel1(root.right, targetSum1); } } //用long是因为测试用例中int出现了溢出。力扣还是恶心人的 public void travel2(TreeNode root,long targetSum2){ if(root==null){ return; } if(targetSum2-root.val==0){ ans++; } if(root.left!=null){ travel2(root.left, targetSum2-root.val); } if(root.right!=null){ travel2(root.right, targetSum2-root.val); } }}

总结：

把三道路径总和的题目放在一起整理，主要是这三道题目包含了很多重要的知识点。二叉树的DFS，回溯算法，递归问题，以及递归问题中的返回值问题等等并且难度层层递进，非常有代表性。