软件设计师-字符串-数组-矩阵

字符串、数组与矩阵

一、字符串00:02

1. 字符串的基本概念02:12

• 特殊线性表：字符串是一种特殊的线性表，其数据元素都为字符（如abcd等字母字符）
• 空串与空格串区别：
  • 空串：长度为0的字符串，没有任何字符
  • 空格串：由一个或多个空格组成的串，空格是空白字、7
  • 47符，占一个字符长度
• 子串定义：
  • 子串：串中任意长度的连续字符构成的序列
  • 主串：含有子串的串
  • 空串是任意串的子串
• 模式匹配：子串的定位操作，用于查找子串在主串中第一次出现位置的算法
• 模式匹配算法（暴力算法）：
  • 原理：逐字符对比，失败就回溯主串指针
  • 问题：效率低（时间复杂度 $O(n\ast m)$）
  • 示例：
    主串：A B A B A B A B
    子串：A B A B C
    当匹配到第5个字符失败时，主串指针需回溯到第2位重新匹配（匹配过程演示 ）

2. KMP算法04:31

• 改进思想：
  • 当匹配过程中出现字符不相等时，不需要回溯主串指针
  • 利用已得到的\"部分匹配\"结果将模式串向右\"滑动\"尽可能远的距离
• 核心优势：
  • 主串指针不回溯，仅模式串指针移动
  • 通过next函数预先计算滑动距离，避免重复比较
• 滑动原理：
  • 找到模式串前缀与主串已匹配部分的后缀的重复部分
  • 将模式串直接滑动到重复部分对齐的位置
• 示例说明：
  • 主串\"ABABABABC\"与模式串\"ABABABC\"匹配时
  • 当第七个字符不匹配时，发现\"ABABAB\"与模式串前缀\"ABABAB\"重复
  • 直接将模式串滑动到主串第四个字符位置继续比较

3. 应用案例10:55

1）例题：next函数计算（考试重点）

2）题目解析

• next函数定义：
  n e x t [ j ] = { 0 j = 1 max ⁡ { k ∣ 1 < k < j , ′ p 1 p 2 ⋯ p k − 1 ′ = ′ p j − k + 1 p j − k + 2 ⋯ p j − 1 ′ } 匹配成功 1 其他情况 next[j] = \\begin{cases} 0 & j=1 \\\\\\max\\{k|1<k<j,\'p_1p_2\\cdots p_{k-1}\'=\'p_{j-k+1}p_{j-k+2}\\cdots p_{j-1}\'\\} & \\text{匹配成功} \\\\1 & \\text{其他情况}\\end{cases} next[j]=⎩ ⎨ ⎧​0max{k∣1<k<j,′p1​p2​⋯pk−1′​=′pj−k+1​pj−k+2​⋯pj−1′​}1​j=1匹配成功其他情况​
• 计算步骤：
  • $j=1$ 时固定为0
  • $j=2$ 时k无解，取1（k是字符串的下标，只能为正整数）
  • $j=3$ 时比较 p 1 ≠ p 2 p_1 \\neq p_2 p1​=p2​，取1
  • $j=4$ 时k=2满足 p 1 = p 3 p_1=p_3 p1​=p3​，取2
  • $j=5$ 时k=2满足 p 1 = p 4 p_1=p_4 p1​=p4​，取2
• 答案验证：
  • 模式串\"abaac\"的next值为$[0,1,1,2,2]$
  • 对应选项B(01122)
• 关键技巧：
  • 注意字符串编号从1开始
  • 比较前缀和后缀时要严格匹配字符顺序
  • 当k有多个可能值时取最大值

二、数组19:37

1. 数组概念

2. 数组的存储地址计算（考点）21:26

• 本质特征：数组是定长线性表在维度上的扩展，属于\"同构\"数据结构（元素类型相同、结构一致）
• 地址计算原理：起始地址 $a$ + 前面元素个数×单个元素长度 $len$
• 一维数组公式：
  $a[i]$ 的存储地址为 $a+i\times len$（默认从0编号）
• 二维数组公式：
  • 按行存储：$a+(i\times n+j)\times len$
  • 按列存储：$a+(j\times m+i)\times len$
• 特殊值技巧：考试时可通过代入具体行列值验证公式，无需死记硬背
• 编号注意点：题目未说明时默认从0开始编号（计算机编码习惯）

三、矩阵28:06

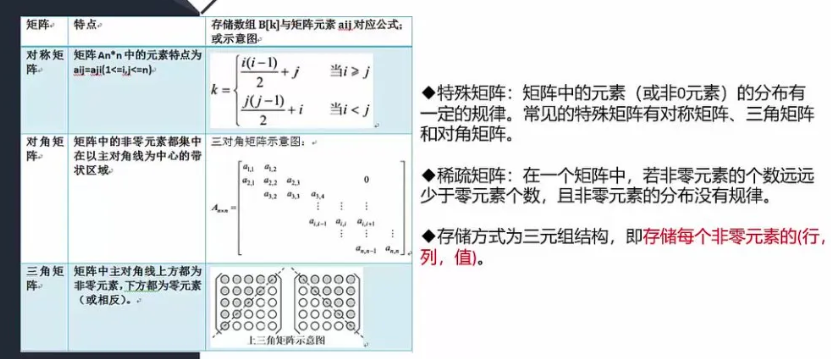
1. 矩阵类型

• 对称矩阵：满足 a i j= a j i a_{ij}=a_{ji} aij​=aji​，沿主对角线对称
• 对角矩阵：非零元素集中在主对角线为中心的带状区域
• 三角矩阵：
  • 上三角：主对角线下方全为零
  • 下三角：主对角线上方全为零
• 稀疏矩阵：非零元素远少于零元素且分布无规律，适合特殊存储方式

2. 应用案例30:56

• 大家自己试试做一下，私信我给答案！！！