LeetCode 25：K 个一组翻转链表

LeetCode 25：K 个一组翻转链表

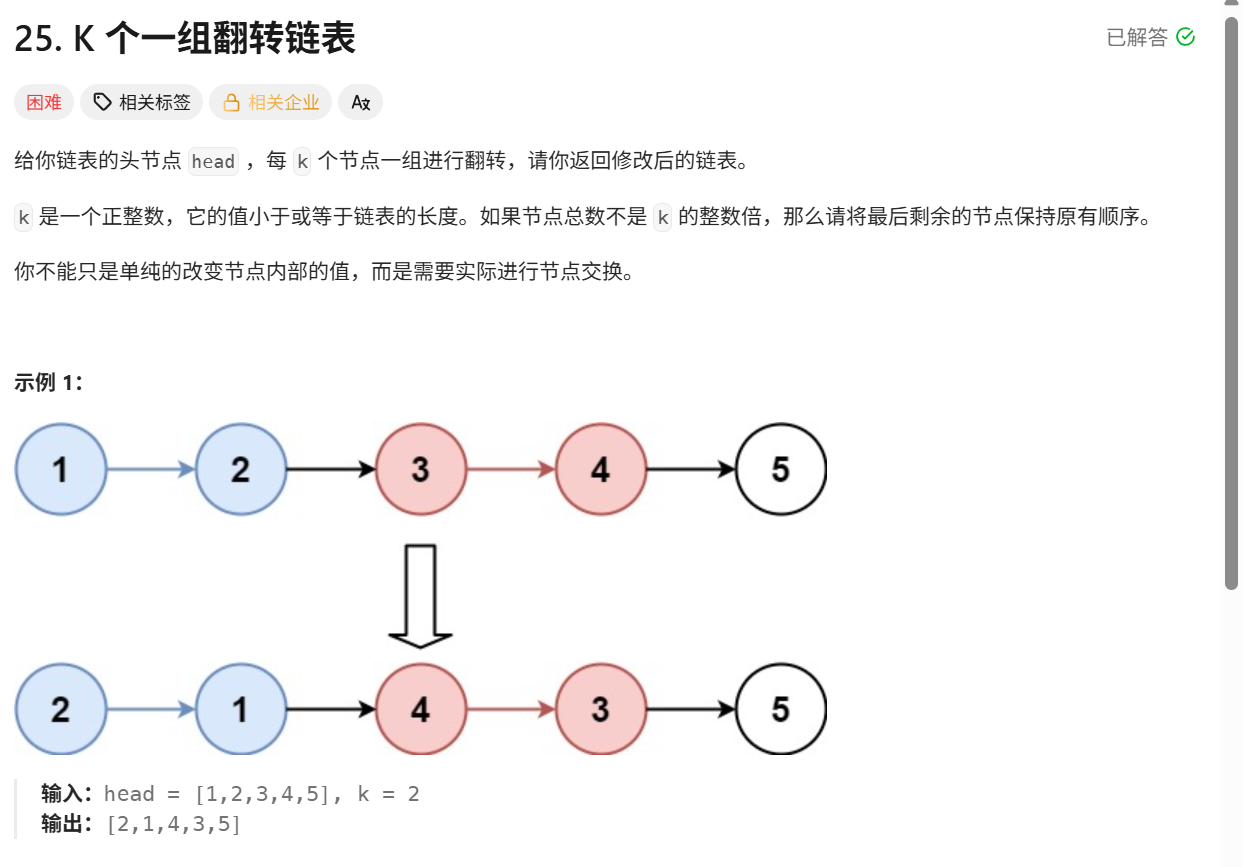
问题定义与核心挑战

给定链表头节点 head 和整数 k，要求 每 k 个节点一组翻转链表，不足 k 个的节点保持原序。例如：

• 输入：head = [1,2,3,4,5], k=2 → 输出：[2,1,4,3,5]
• 输入：head = [1,2,3,4,5], k=3 → 输出：[3,2,1,4,5]

核心挑战：

1. 分组与边界判断：如何确定每组的范围（找到尾节点），并处理不足 k 个节点的情况。
2. 链表反转：如何高效反转每组内的节点，并连接前后部分。
3. 递归与迭代的平衡：递归思路更直观，但需理解栈的调用逻辑。

核心思路：递归 + 局部反转

1. 分组定位：找到当前组的尾节点（从 head 出发走 k-1 步），若不足 k 个节点则直接返回。
2. 局部反转：反转当前组内的节点（从 head 到尾节点）。
3. 递归连接：将反转后的组与剩余链表（尾节点的下一个节点开始）递归处理的结果连接。

算法步骤详解

步骤 1：定位当前组的尾节点

• 从 head 出发，移动 k-1 次，找到当前组的尾节点 tail。
• 若移动过程中 tail 变为 null，说明剩余节点不足 k 个，直接返回 head（无需翻转）。

ListNode tail = head;for (int i = 0; i < k - 1; i++) { if (tail == null) return head; // 不足k个，直接返回 tail = tail.next;}if (tail == null) return head; // 双重保险（罕见情况）

步骤 2：保存剩余链表并反转当前组

• 剩余链表的头节点为 tail.next（记为 rest）。
• 反转当前组（head 到 tail），得到新的头节点 newHead（原 tail）。

ListNode rest = tail.next; // 剩余链表的头ListNode newHead = reverse(head, tail); // 反转当前组

步骤 3：递归处理剩余链表并连接

• 递归处理剩余链表 rest，得到处理后的头节点 restHead。
• 将当前组的尾节点（原 head）连接到 restHead。

ListNode restHead = reverseKGroup(rest, k); // 递归处理剩余部分head.next = restHead; // 连接反转后的尾（原head）与剩余部分return newHead; // 返回当前组反转后的头（原tail）

步骤 4：实现局部反转函数 reverse

反转从 head 到 tail 的链表，返回新的头节点（原 tail）：

• 用三指针法（prev, curr, next）逐步反转节点。
• 最后处理尾节点 tail，使其指向反转后的前一个节点。

private ListNode reverse(ListNode head, ListNode tail) { ListNode prev = null; ListNode curr = head; while (curr != tail) { // 遍历到尾节点前一个 ListNode next = curr.next; curr.next = prev; // 反转指针 prev = curr; curr = next; } curr.next = prev; // 处理尾节点 return curr; // 新头是原tail}

完整代码（Java）

/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode() {} * ListNode(int val) { this.val = val; } * ListNode(int val, ListNode next) { this.val = val; this.next = next; } * } */class Solution { public ListNode reverseKGroup(ListNode head, int k) { // 边界处理：空链表或k=1（无需翻转） if (head == null || k == 1) { return head; } // 步骤1：定位当前组的尾节点 ListNode tail = head; for (int i = 0; i < k - 1; i++) { if (tail == null) { // 不足k个节点，直接返回 return head; } tail = tail.next; } if (tail == null) { // 双重检查（理论上不会触发） return head; } // 步骤2：保存剩余链表，反转当前组 ListNode rest = tail.next; // 剩余链表的头 ListNode newHead = reverse(head, tail); // 反转当前组（head->tail） // 步骤3：递归处理剩余链表，连接结果 ListNode restHead = reverseKGroup(rest, k); // 递归处理剩余部分 head.next = restHead; // 原head现在是反转后的尾，连接剩余部分 return newHead; // 返回当前组反转后的头（原tail） } // 辅助函数：反转从head到tail的链表，返回新的头（原tail） private ListNode reverse(ListNode head, ListNode tail) { ListNode prev = null; ListNode curr = head; while (curr != tail) { // 遍历到尾节点前一个 ListNode next = curr.next; curr.next = prev; // 反转指针 prev = curr; curr = next; } curr.next = prev; // 处理尾节点，使其指向反转后的前一个节点 return curr; // 新头是原tail }}

关键逻辑解析

1. 分组定位的细节

• 循环 k-1 次找尾节点：确保当前组恰好有 k 个节点（head 到 tail 共 k 个）。
• 若中途 tail 为 null，说明剩余节点不足 k 个，直接返回（避免无效反转）。

2. 局部反转的三指针法

• prev 初始为 null，curr 从 head 开始，逐步将 curr.next 指向 prev，实现反转。
• 循环结束时，curr 指向 tail，需单独处理 tail 的 next（指向 prev，即反转后的前一个节点）。

3. 递归的作用

• 递归处理剩余链表 rest，天然实现“分组处理”的逻辑，代码更简洁。
• 递归栈的深度为 O(n/k)（每组递归一次），空间复杂度可接受（n 为链表长度）。

4. 链表连接的关键

• 反转后，原 head 变为当前组的尾节点，需将其 next 指向剩余链表的处理结果（restHead）。

示例验证（以示例 1 为例）

输入：head = [1,2,3,4,5], k=2

1. 第一次递归：

   • 定位 tail = 2（head=1 移动 1 次），rest = 3。
   • 反转 1->2 得到 2->1，newHead=2。
   • 递归处理 rest=3，进入第二次递归。

2. 第二次递归：

   • 定位 tail = 4（head=3 移动 1 次），rest = 5。
   • 反转 3->4 得到 4->3，newHead=4。
   • 递归处理 rest=5，进入第三次递归。

3. 第三次递归：

   • 定位 tail 时，head=5 移动 1 次后 tail=null，返回 5。
   • restHead=5，原 head=3（反转后的尾）的 next=5 → 3->5。
   • 返回 4->3->5。

4. 回溯连接：

   • 第二次递归中，原 head=3 的 next=4->3->5 → 1->4->3->5。
   • 第一次递归中，原 head=1 的 next=4->3->5 → 2->1->4->3->5。

复杂度分析

• 时间复杂度：O(n)。每个节点被访问两次（一次定位尾节点，一次反转）。
• 空间复杂度：O(n/k)。递归栈的深度为分组数（最坏情况 n/k 层，如 k=1 时退化为 O(n)，但题目中 k≥1 且 k≤n）。

该方法通过 递归分组 + 局部反转，巧妙地将复杂的链表操作分解为子问题，代码简洁且逻辑清晰，是链表类问题的经典解法。