图论-最短路 Bellman-Ford算法

文章目录

• Bellman-Ford算法
• • SPFA优化
  • 路径记录与传输

Bellman-Ford算法

此算法是基于松弛操作的单源最短路算法。
e[u]存u点的出边的邻边和边权，d[u]存u点到源点的距离。

• 1.初始化，d[s]=0,d[其他点]=INT_MAX。
• 2.执行多轮循环，对所有边都尝试进行一次松弛操作。
• 3.当一轮中没有成功的松弛操作时，算法停止。

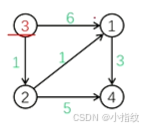
如图，3为源点

代码展示

struct edug{int v,w;}; vector<edge>e[N];int d[N];bool Bellman-Ford(int s){//把所有点到源点的距离初始为无穷大memset(d,0x3f3f3f,sizeof d);d[s]=0;//源点到自身的距离为0bool f;//标记是否有松弛操作for(int i=1;i<=n;i++)//n轮操作 {f=false;for(int u=1;u<=n;u++)//n个点 {if(d[u]==0x3f3f3f)continue;for(auto x:ed[u])//遍历u的出边 {int v=x.v,w=x.w;if(d[u]+w<d[v]){d[v]=d[u]+w;f=true;}}}if(!f)break;//没有得到更新就退出  } return f;//第n轮=true则有环 }int main(){cin>>n>>m>>s;for(int i=0;i<m;i++){cin>>a>>b>>c;e[a].push_back({b,c});}return 0; } 

优点：
可以正确处理负边权。
可以判负环，如果n轮循环后仍存在能松弛的边，则说明存在负环。
时间复杂度:O(nm)

SPFA优化

我们可以想到只有本轮被更新的点，其出边才有可能引起下一轮的松弛操作，因此用队列来维护被更新的点的集合。
vis[u]标记u点是否在队内，cnt[v]记录边数，判负环。

• 1.初始化，s入队，并标记s在队内，d[s]=0,d[其他点]=INT_MAX
• 2.从队头弹出u点，标记u不在队内
• 3.枚举u的所有出边，执行松弛操作，记录s到v的边数，并判负环。如果v不在队内则把v 压入队尾，并标记
• 重复2，3操作，直到队列为空。

代码展示

struct edug{int v,w;}; vector<edge>e[N];int d[N];queue<int>q;bool spfa(int s){memset(d,0x3f3f3f,sizeof d);d[s]=0,vis[s]=1;q.push(s);while(q.size()){int u=q.front();q.pop();vis[u]=0;for(auto x:e[u]){int v=x.v,w=x.w;if(d[u]+w<d[v]){d[v]=d[u]+w;cnt[v]=cnt[u]+1;if(cnt[v]>=n)return true;if(!vis[v])q.push(v),vis[v]=1;}}}return false;}

路径记录与传输

void dfs_path(int u){if(u==1){cout<<u<<\" \";return ;}dfs_path(pre[u]);cout<<u<<\" \";}