贪心算法Day3学习心得
今天继续看贪心的题目
第一道:1005. K 次取反后最大化的数组和 - 力扣(LeetCode)
给定一个整数数组 A,我们只能用以下方法修改该数组:我们选择某个索引 i 并将 A[i] 替换为 -A[i],然后总共重复这个过程 K 次。(我们可以多次选择同一个索引 i。)
以这种方式修改数组后,返回数组可能的最大和。
贪心的思路,局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。
局部最优可以推出全局最优。
那么如果将负数都转变为正数了,K依然大于0,此时的问题是一个有序正整数序列,如何转变K次正负,让 数组和 达到最大。
那么又是一个贪心:局部最优:只找数值最小的正整数进行反转,当前数值和可以达到最大(例如正整数数组{5, 3, 1},反转1 得到-1 比 反转5得到的-5 大多了),全局最优:整个 数组和 达到最大。
- 第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
- 第二步:从前向后遍历,遇到负数将其变为正数,同时K--
- 第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
- 第四步:求和
对应C++代码如下:
class Solution {static bool cmp(int a, int b) { return abs(a) > abs(b);}public: int largestSumAfterKNegations(vector& A, int K) { sort(A.begin(), A.end(), cmp); // 第一步 for (int i = 0; i < A.size(); i++) { // 第二步 if (A[i] 0) { A[i] *= -1; K--; } } if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步 int result = 0; for (int a : A) result += a; // 第四步 return result; }};然后是第二道:134. 加油站 - 力扣(LeetCode)
这道题原来好像也写过。
暴力的方法很明显就是O(n^2)的,遍历每一个加油站为起点的情况,模拟一圈。
如果跑了一圈,中途没有断油,而且最后油量大于等于0,说明这个起点是ok的。
暴力的方法思路比较简单,但代码写起来也不是很容易,关键是要模拟跑一圈的过程。
for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历。
C++代码如下:
class Solution {public: int canCompleteCircuit(vector& gas, vector& cost) { for (int i = 0; i 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了) rest += gas[index] - cost[index]; index = (index + 1) % cost.size(); } // 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置 if (rest >= 0 && index == i) return i; } return -1; }};直接从全局进行贪心选择,情况如下:
-
情况一:如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
-
情况二:rest[i] = gas[i]-cost[i]为一天剩下的油,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
-
情况三:如果累加的最小值是负数,汽车就要从非0节点出发,从后向前,看哪个节点能把这个负数填平,能把这个负数填平的节点就是出发节点。
C++代码如下:
class Solution {public: int canCompleteCircuit(vector& gas, vector& cost) { int curSum = 0; int min = INT_MAX; // 从起点出发,油箱里的油量最小值 for (int i = 0; i < gas.size(); i++) { int rest = gas[i] - cost[i]; curSum += rest; if (curSum < min) { min = curSum; } } if (curSum = 0) return 0; // 情况2 // 情况3 for (int i = gas.size() - 1; i >= 0; i--) { int rest = gas[i] - cost[i]; min += rest; if (min >= 0) { return i; } } return -1; }};可以换一个思路,首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum。
那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新i,那么起始位置又变成新的i+1了。
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢?
如果 curSum<0 说明 区间和1 + 区间和2 0。
区间和1 + 区间和2 0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择起始位置了。
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
局部最优可以推出全局最优,找不出反例,试试贪心!
C++代码如下:
class Solution {public: int canCompleteCircuit(vector& gas, vector& cost) { int curSum = 0; int totalSum = 0; int start = 0; for (int i = 0; i < gas.size(); i++) { curSum += gas[i] - cost[i]; totalSum += gas[i] - cost[i]; if (curSum < 0) { // 当前累加rest[i]和 curSum一旦小于0 start = i + 1; // 起始位置更新为i+1 curSum = 0; // curSum从0开始 } } if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了 return start; }};然后是最后一道:135. 分发糖果 - 力扣(LeetCode)
局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
局部最优可以推出全局最优。
如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个,所以贪心:candyVec[i] = candyVec[i - 1] + 1
代码如下:
// 从前向后for (int i = 1; i ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;}如图:
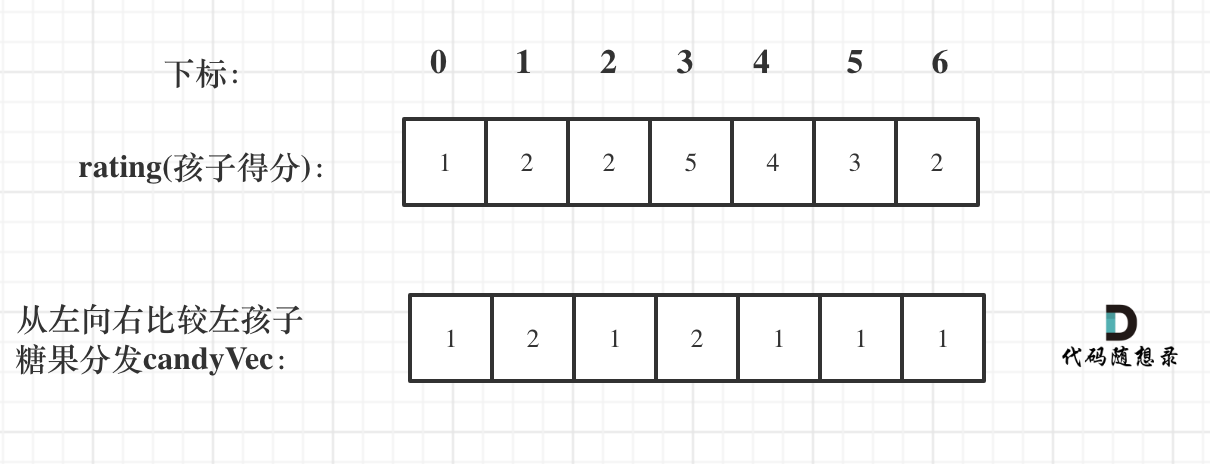
再确定左孩子大于右孩子的情况(从后向前遍历)
为什么不能从前向后遍历呢?因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果,所以 要从后向前遍历。
所以确定左孩子大于右孩子的情况一定要从后向前遍历!
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
那么又要贪心了,局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
局部最优可以推出全局最优。
所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。
所以该过程代码如下:
// 从后向前for (int i = ratings.size() - 2; i >= 0; i--) { if (ratings[i] > ratings[i + 1] ) { candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1); }}整体代码如下:
class Solution {public: int candy(vector& ratings) { vector candyVec(ratings.size(), 1); // 从前向后 for (int i = 1; i ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1; } // 从后向前 for (int i = ratings.size() - 2; i >= 0; i--) { if (ratings[i] > ratings[i + 1] ) { candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1); } } // 统计结果 int result = 0; for (int i = 0; i < candyVec.size(); i++) result += candyVec[i]; return result; }};

