【算法基础】位运算

1. 基础位运算

异或，同 0 异 1（相加不进位）

        现给一个整数 n，其二进制表示从最低位开始计数为 0 - 31，有如下问题：

        确定其二进制表示的第 x 位是 0 还是 1：

        将第 x 位修改为 1：

        将第 x 位修改为 0：

        lowbit 运算（提取最低位的 1）：

        将最右侧的 1 变为 0：

        可以用 n 减去 lowbit 运算后的结果，也可以使用下面的方法：

2. 十进制快速转化二进制

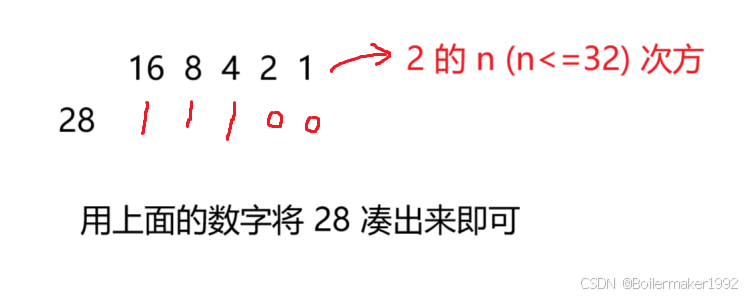
3. 巧用异或

        对于异或运算，有如下规律：

        a ^ 0 = a

        a ^ a = 0，这表示两个相同的数经过异或运算会变为 0，由此有 b ^ a ^ a = b，成对的相同的数字会被消掉。

        a ^ b ^ c = a ^ ( b ^ c )，这表示多个数进行异或运算可以忽略顺序，得到的结果唯一。

268. 丢失的数字 - 力扣（LeetCode）

class Solution { public int missingNumber(int[] nums) { int len = nums.length; int target = 0; for (int i = 0; i <= len; i++) { target ^= i; } for (int i = 0; i < len; i++) { target ^= nums[i]; } return target; }}

260. 只出现一次的数字 III - 力扣（LeetCode）

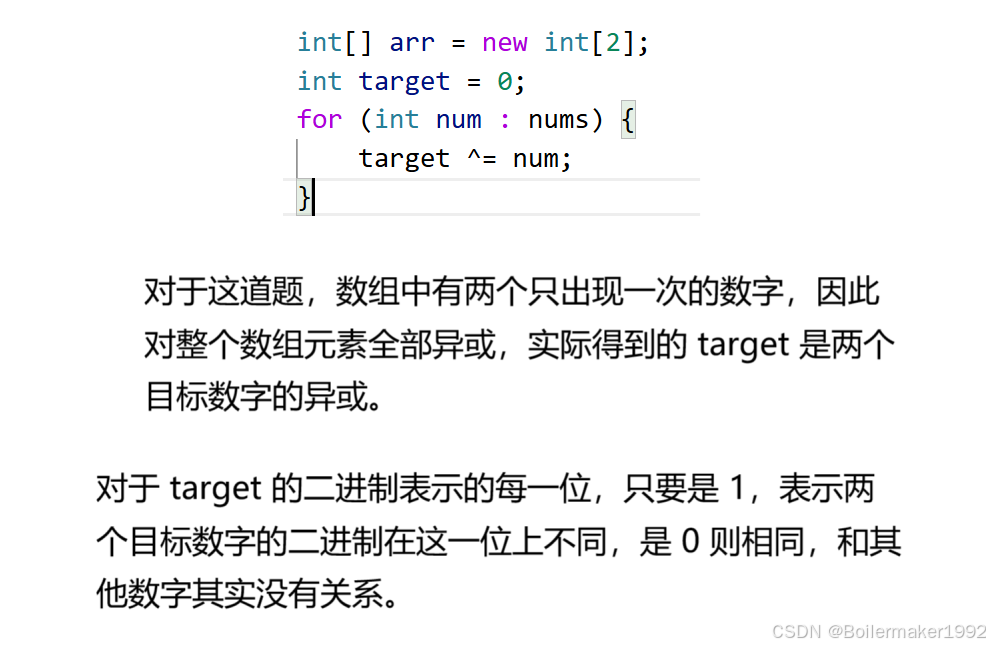
371. 两整数之和 - 力扣（LeetCode）

面试题 17.19. 消失的两个数字 - 力扣（LeetCode）

        这道题的思路和 “只出现一次的数字3“ 一致。首先通过两遍异或可以得出两个消失数字的异或值。

 int n = nums.length + 2; int exc = 0; for (int i = 1; i <= n; i++) { exc ^= i; } for (int num : nums) { exc ^= num; }

        得到这两个数异或后的值，即 exc，进一步就可以知道这两个数的哪位比特位是不同的，通过随便一个不同的比特位可以把整个数组分成两部分，而这两个缺失的数字一定被分在不同的部分中。

 int diff = 0; for (int i = 0; i > i & 1) == 1) { diff = i; break; } }

        现在找了到最左侧的值为 1 的比特位，即 diff。

        接下来将数组分组异或。

 int t1 = 0, t2 = 0; for (int num : nums) { if ((num >> diff & 1) == 1) { t1 ^= num; } else { t2 ^= num; } }

        再用 diff 位为 0 或 1 的连续数字异或一遍，就将缺少的数字筛出来了。

 for (int i = 1; i > diff & 1) == 1) { t1 ^= i; } else { t2 ^= i; } }

4. 位图

面试题 01.01. 判定字符是否唯一 - 力扣（LeetCode）  

        利用位图的思想，一个整数的二进制表示有 32 个比特位，每一位都可以用于记录 0 1 这样的信息，相当于 hash 表。

5. 只出现一次的数字

        某数组中除其中一个元素只出现一次，其余元素均出现 n 次，使用线性时间和常数空间找到这个只出现一次的元素。

class Solution { public int singleNumber(int[] nums) { int temp = 0; // 外层每次计算 temp 的其中一位比特位，共需 32 次 for (int i = 0; i < 32; i++) { int sum = 0; // 内层遍历数组 for (int j = 0; j > i) & 1; } temp += (sum % 3) << i; } return temp; // 该解法共需遍历数组 32 次 }}

        本题尚可用交换机。