网站导航
> 技术文档 > 【数据结构】栈与队列：数据结构中的双生子

【数据结构】栈与队列：数据结构中的双生子

网友: 技术文档 2025-09-02 19:05:51

【数据结构】栈与队列：数据结构中的双生子

栈与队列：数据结构中的双生子

✨前言：在数据结构的学习中，栈(Stack) 与 队列(Queue) 是两种基础而强大的存在。它们看似简单，却在各种算法和系统设计中扮演着核心角色。理解它们的特性和实现原理，是每位程序员成长的必经之路。今天我将带大家深入学习栈和队列。
📖专栏：【数据结构】

目录

  • 栈与队列：数据结构中的双生子
    • 一、栈（Stack）：后进先出的数据世界
      • 1.1 栈的核心概念
      • 1.2 栈的实现方式
    • 二、队列（Queue）：先进先出的公平机制
      • 2.1 队列的核心概念
      • 2.2 队列的实现方式
    • 三、总结

一、栈（Stack）：后进先出的数据世界

1.1 栈的核心概念

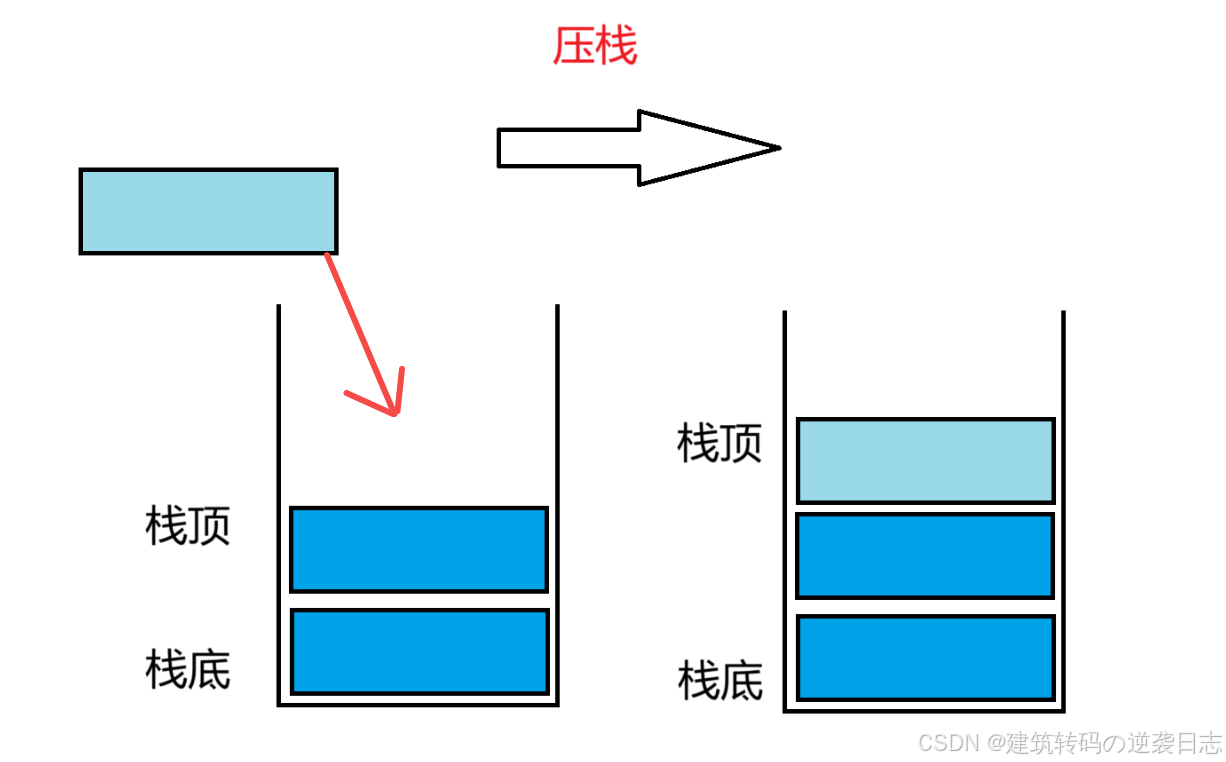
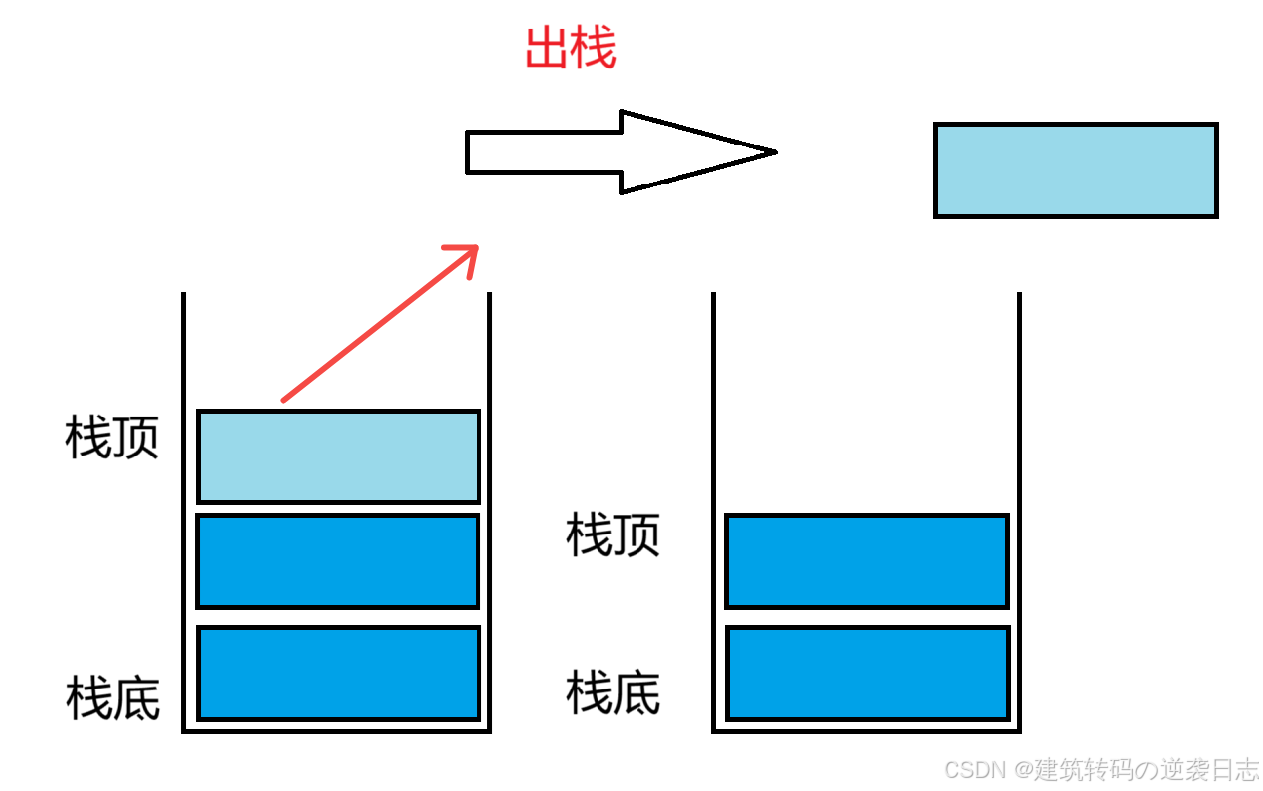
栈是一种特殊的线性表，遵循LIFO（Last In First Out）原则，即最后入栈的元素最先出栈。它只允许在固定的一端（称为栈顶）进行插入（压栈）和删除（出栈）操作，另一端称为栈底。

  • 压栈（Push）：向栈顶添加元素

【数据结构】栈与队列：数据结构中的双生子

  • 出栈（Pop）：从栈顶移除元素

【数据结构】栈与队列：数据结构中的双生子

1.2 栈的实现方式

栈可以通过数组或链表实现，数组实现通常更优，因为：

  • 数组在尾部插入/删除的时间复杂度为O(1)
  • 内存连续，缓存命中率高
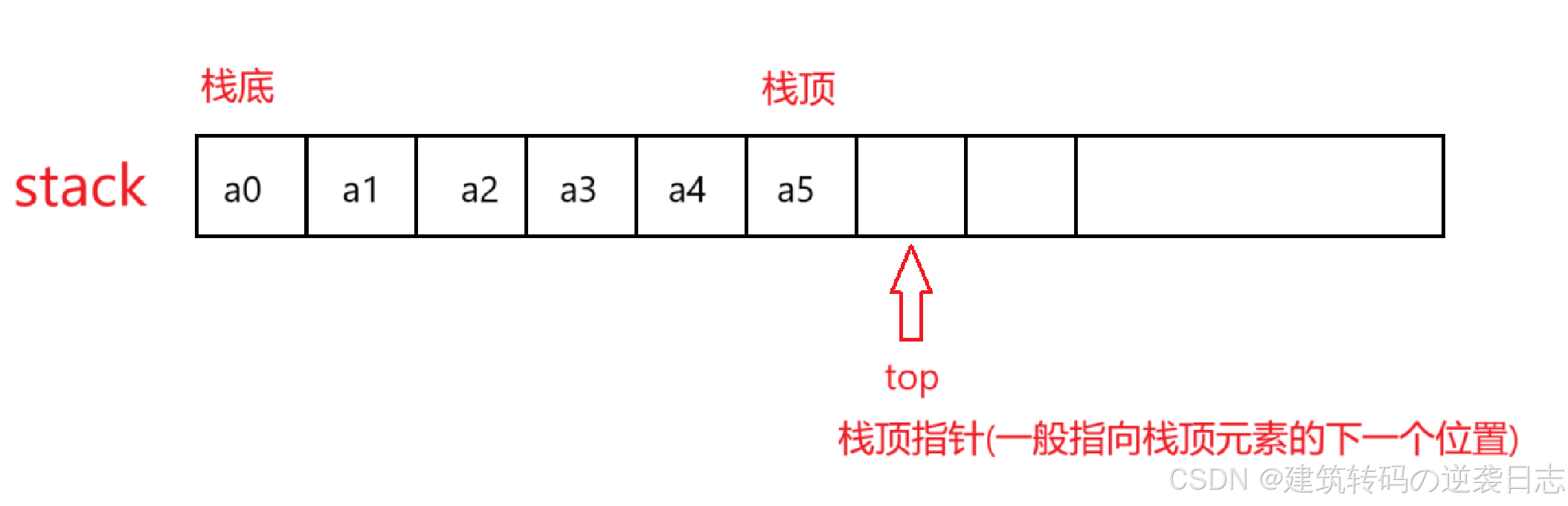
    【数据结构】栈与队列：数据结构中的双生子

对于栈顶指针一般指向指向栈顶元素的下一个位置解释：

一般来说，栈顶指针可以指向栈顶元素，那这样的话栈为空的情况，top就只能指向-1了，看起来很别扭，所以为了方便起见，直接让栈顶指针指向指向栈顶元素的下一个位置就行。

1. 栈结构定义和初始化

#include #include #include #include typedef int STDataType; // 栈存储的数据类型// 栈结构体typedef struct Stack { STDataType* a; // 动态数组存储栈元素 int top; // 栈顶指针(指向栈顶元素的下一个位置) int capacity; // 当前分配的存储容量} Stack;#define INIT_SIZE 4 // 初始容量大小// 初始化栈void StackInit(Stack* ps) { assert(ps != NULL); // 安全检查 ps->a = NULL; // 初始时数组为空 ps->top = 0; // 栈顶指针初始为0 ps->capacity = 0; // 初始容量为0}

2. 容量检查函数（内部使用）

// 检查并扩容栈（内部函数）static void CheckCapacity(Stack* ps) { assert(ps != NULL); // 当栈满时需要扩容 if (ps->capacity == ps->top) { // 计算新容量：初始为INIT_SIZE，否则双倍扩容 int newCapacity = (ps->capacity == 0) ? INIT_SIZE : ps->capacity * 2; // 重新分配内存 STDataType* tmp = (STDataType*)realloc(ps->a, newCapacity * sizeof(STDataType)); if (tmp == NULL) { perror(\"栈扩容失败\"); exit(EXIT_FAILURE); } ps->a = tmp; ps->capacity = newCapacity; printf(\"栈已扩容至%d\\n\", newCapacity); // 调试信息 }}

3. 入栈操作

// 元素入栈void StackPush(Stack* ps, STDataType data) { assert(ps != NULL); // 安全检查 // 检查是否需要扩容 CheckCapacity(ps); // 将元素放入栈顶位置 ps->a[ps->top] = data; ps->top++; // 栈顶指针上移 printf(\"元素%d入栈成功\\n\", data); // 调试信息}

4. 出栈操作

// 元素出栈void StackPop(Stack* ps) { // 安全检查：栈不能为空 assert(ps != NULL && !StackEmpty(ps)); printf(\"元素%d出栈\\n\", StackTop(ps)); // 调试信息 ps->top--; // 栈顶指针下移}

5. 获取栈顶元素

// 获取栈顶元素STDataType StackTop(Stack* ps) { // 安全检查：栈不能为空 assert(ps != NULL && !StackEmpty(ps)); return ps->a[ps->top - 1]; // 返回栈顶元素}

6. 获取栈大小

// 获取栈中元素数量int StackSize(Stack* ps) { assert(ps != NULL); return ps->top; // 栈顶指针就是元素数量}

7. 判断栈是否为空

// 检查栈是否为空bool StackEmpty(Stack* ps) { assert(ps != NULL); return ps->top == 0; // 栈顶为0表示空栈}

8. 销毁栈

// 销毁栈void StackDestroy(Stack* ps) { assert(ps != NULL); free(ps->a); // 释放动态数组 ps->a = NULL; // 避免野指针 ps->top = 0; // 重置栈顶指针 ps->capacity = 0; // 重置容量 printf(\"栈已销毁\\n\"); // 调试信息}

二、队列（Queue）：先进先出的公平机制

2.1 队列的核心概念

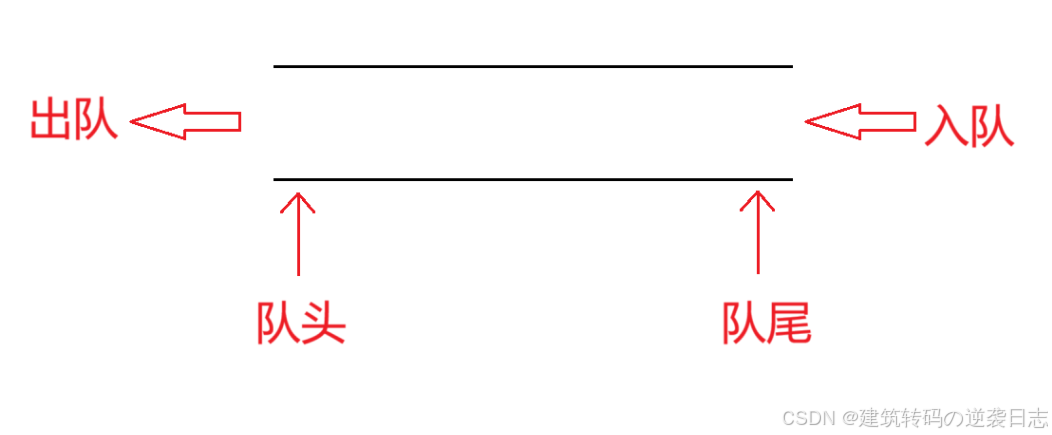
队列是另一种特殊的线性表，遵循FIFO（First In First Out）原则，即最先入队的元素最先出队。插入操作在队尾进行，删除操作在队头进行。

  • 入队（Enqueue）：向队尾添加元素
  • 出队（Dequeue）：从队头移除元素

【数据结构】栈与队列：数据结构中的双生子

2.2 队列的实现方式

队列通常使用链表实现更优，因为：

  • 数组实现时，头部删除需要移动元素（O(n)）
  • 链表在头部删除和尾部插入都是O(1)

1. 队列结构定义

#include #include #include #include typedef int QDataType; // 队列元素类型// 队列节点结构typedef struct QueueNode { QDataType data;  // 数据域 struct QueueNode* next; // 指向下一个节点} QNode;// 队列结构typedef struct Queue { QNode* phead; // 队头指针 QNode* ptail; // 队尾指针 int size; // 队列元素个数} Queue;

2. 队列初始化

// 初始化队列 void QueueInit(Queue* q) { assert(q); // 确保队列指针有效 q->phead = q->ptail = NULL; // 初始时头尾指针都为空 q->size = 0;  // 初始大小为0}

3. 入队操作

// 队尾入队列 void QueuePush(Queue* q, QDataType data) { assert(q); // 确保队列指针有效 // 创建新节点 QNode* newnode = (QNode*)malloc(sizeof(QNode)); if (newnode == NULL) { perror(\"malloc fail\"); exit(1); } newnode->data = data; // 设置节点数据 newnode->next = NULL; // 新节点next置空 // 队列为空时的特殊处理 if (q->phead == NULL) { q->phead = q->ptail = newnode; } else { q->ptail->next = newnode; // 原尾节点指向新节点 q->ptail = newnode; // 更新尾指针 } q->size++; // 队列大小增加}

4. 出队操作

// 队头出队列 void QueuePop(Queue* q) { assert(q && q->phead != NULL); // 确保队列不为空 QNode* pop = q->phead; // 保存要删除的节点 q->phead = q->phead->next; // 头指针后移 free(pop);  // 释放原头节点 pop = NULL; // 避免野指针 // 如果出队后队列为空，更新尾指针 if (q->phead == NULL) { q->ptail = NULL; } q->size--; // 队列大小减少}

5. 获取队头元素

// 获取队列头部元素 QDataType QueueFront(Queue* q) { assert(q && q->phead); // 确保队列不为空 return q->phead->data; // 返回头节点数据}

6. 获取队尾元素

// 获取队列队尾元素 QDataType QueueBack(Queue* q) { assert(q && q->ptail); // 确保队列不为空 return q->ptail->data; // 返回尾节点数据}

7. 获取队列大小

// 获取队列中有效元素个数 int QueueSize(Queue* q) { assert(q); // 确保队列指针有效 return q->size; // 直接返回size成员}

8. 检查队列是否为空

// 检测队列是否为空bool QueueEmpty(Queue* q) { assert(q); // 确保队列指针有效 return q->size == 0; // size为0表示空队列}

9. 销毁队列

// 销毁队列 void QueueDestroy(Queue* q) { assert(q); // 确保队列指针有效 QNode* pcur = q->phead; // 从头节点开始 QNode* next = NULL; // 保存下一个节点 // 遍历释放所有节点 while (pcur) { next = pcur->next; // 保存下一个节点 free(pcur); // 释放当前节点 pcur = next; // 移动到下一个节点 } // 重置队列状态 q->phead = q->ptail = NULL; q->size = 0;}

三、总结

栈和队列虽然操作规则截然不同，但它们都是线性数据结构的基础构件。栈的LIFO特性使其成为处理递归和回溯的理想选择，而队列的FIFO特性则完美匹配需要公平处理的场景。理解它们的核心概念和实现细节，能够帮助我们更好地设计算法和解决实际问题。这两种看似简单的数据结构，共同构建了计算机科学中无数复杂系统的基石。

如果本文对您有启发：
✅ 点赞 - 让更多人看到这篇硬核技术解析 ！
✅ 收藏 - 实战代码随时复现
✅ 关注 - 获取数据结构系列深度更新
您的每一个[三连]都是我们持续创作的动力！✨

【数据结构】栈与队列：数据结构中的双生子

网络标签：

相关问题