动态规划精讲：完全背包问题的理论、优化与“零钱兑换”等模型应用

53.完全背包【模版】

完全背包
你有一个背包，最多能容纳的体积是V。

现在有n种物品，每种物品有任意多个，第i种物品的体积为vivi​ ,价值为wiwi​。

（1）求这个背包至多能装多大价值的物品？

（2）若背包恰好装满，求至多能装多大价值的物品？

输入描述：
第一行两个整数n和V，表示物品个数和背包体积。

接下来n行，每行两个数vivi​和wiwi​，表示第i种物品的体积和价值。

1≤n,V≤10001≤n,V≤1000

输出描述：
输出有两行，第一行输出第一问的答案，第二行输出第二问的答案，如果无解请输出0。


dp[i] [j]表示：从前i个物品中选，总体积不超过j，所有选法中，最大的价值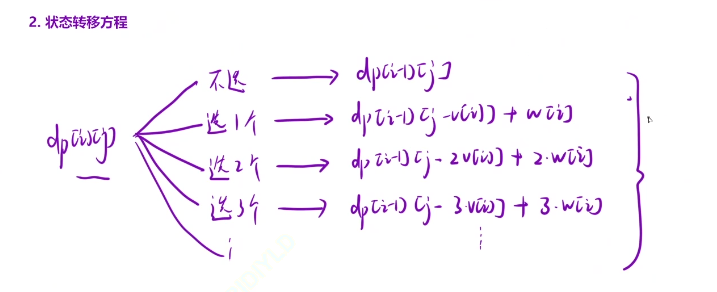

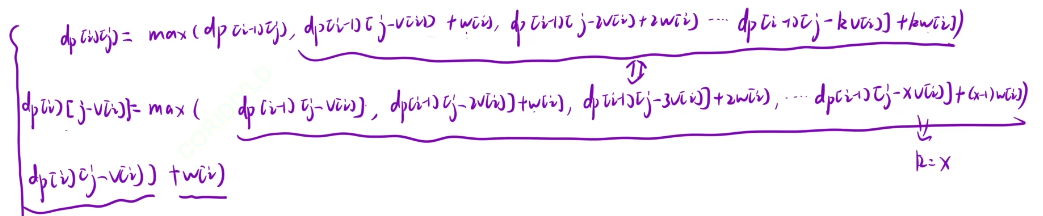
那么最终的动态规划表达式就是在合格

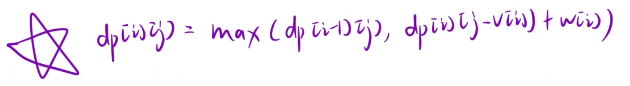
i位置存在选和不选，选的话存在选多少个的情况

初始化可以不用，都初始化为0就行了

这个第一问的问题是从所有的物品中去选，求这个背包至多能装多大价值的物品，就是最大价值不超过V
所以这个的返回值就是dp[n] [v]

第二问是总体积一定要等于j的
若背包恰好装满，求至多能装多大价值的物品？
dp[i] [j]表示：从前i个物品中选，总体积恰好是j，所有选法中，最大的价值
我们在一开始初始化的时候加上一个状态，就是-1，-1就是表示当前的这个物品是不能凑到j-v[i]的体积的

就是dp[i] [j-v[i]]!=-1的情况才能进行后续的操作

初始化的话我们还是仅仅只是需要修改第一行就行了，初始化如下

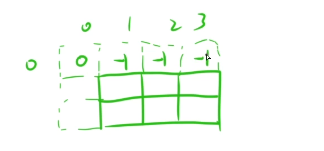
返回值的话就是dp[n][V]== -1?0:dp[n][v]
如果是-1的话，那么就返回0，如果不是-1的话那么就返回dp[n] [v]就行了

#include #includeusing namespace std; const int N=1010; int n,V,v[N],w[N];int dp[N][N];int main(){    //读入数据    cin>>n>>V;    for(int i=1;i>v[i]>>w[i];    }     //解决第一问    //这里我们是不需要进行初始化操作的    for(int i=1;i<=n;i++)    {        for(int j=0;j=0)dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);//我们这里是完全背包，所以我们这里是dp[i]的,我们这里就是选择i位置的，选多少个i位置的物品，那么总体归纳起来就是dp[i][j-v[i]]+w[i]        }    }    cout<<dp[n][V]<<endl;     //我们现在需要重新用dp表，所以需要将这个进行清空的操作    memset(dp,0,sizeof dp);    //初始化，我们需要将第一行除了第一个位置都初始化为-1，-1这个状态表示的就是这个位置是不能凑到j-v[i]的，就是不行的    for(int i=1;i<=V;i++)dp[0][i]=-1;//都初始化为-1     for(int i=1;i<=n;i++)    {        for(int j=0;j=0&&dp[i][j-v[i]]!=-1)dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);//我们这里是完全背包，所以我们这里是dp[i]的,我们这里就是选择i位置的，选多少个i位置的物品，那么总体归纳起来就是dp[i][j-v[i]]+w[i]        }    }    //我们输出结果的时候是不能进行直接输出的，我们是需要进行判断操作的    cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;     return 0;}

这里进行下总结：
第一问是求这个背包至多能装多大价值的物品
就是体积j不超过V就行了，
我们完全背包的物品是有个数的，我们可以挑选i这个位置的物品，也是可以不挑选的，可以挑选1个，2个甚至k个

这个就是和我们01背包是截然不同的区别

那么我们i位置物品不选的情况就是

如果我们选择了i位置的话，存在选多少个的情况，那么都包含在下面的dp状态中了

为什么是是这样的，可以参考下面的图片

第二问是若背包恰好装满，求至多能装多大价值的物品
就是说我们的j要恰好等于V
所以我们是需要在初始化的时候加上-1这个状态的
就是表示这个dp位置是不能凑到dp[i] [j-v[i]]的，所以我们 就得进行一个判断了，看看这个位置是否为-1，必须不等于-1才能进行后面的操作

返回值也是的，我们需要判断这个位置是否为-1，如果是-1的话就返回0，如果不是-1的话就正常返回值就行了

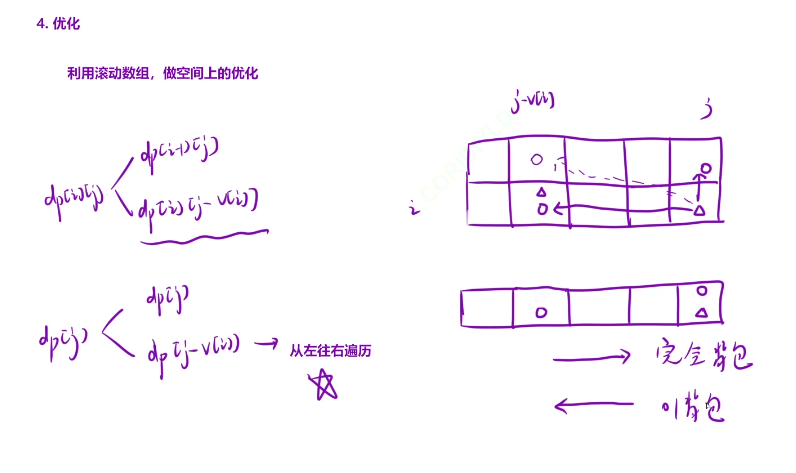
下面是进行空间优化后的代码，将横坐标都删除了
完全背包是从左往右进行遍历的
01背包是从右往左进行遍历的

#include #includeusing namespace std; const int N=1010; int n,V,v[N],w[N];int dp[N];int main(){    //读入数据    cin>>n>>V;    for(int i=1;i>v[i]>>w[i];    }     //解决第一问    //这里我们是不需要进行初始化操作的    for(int i=1;i<=n;i++)    {        for(int j=v[i];j=0)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);//我们这里是完全背包，所以我们这里是dp[i]的,我们这里就是选择i位置的，选多少个i位置的物品，那么总体归纳起来就是dp[i][j-v[i]]+w[i]        }    }    cout<<dp[V]<<endl;     //我们现在需要重新用dp表，所以需要将这个进行清空的操作    memset(dp,0,sizeof dp);    //初始化，我们需要将第一行除了第一个位置都初始化为-1，-1这个状态表示的就是这个位置是不能凑到j-v[i]的，就是不行的    for(int i=1;i<=V;i++)dp[i]=-1;//都初始化为-1     for(int i=1;i<=n;i++)    {        for(int j=v[i];j<=V;j++)//我们从0开始进行计数，因为我们是没有初始化第一列的        {            //这里的话我们因为需要恰好凑到j，所以我们在使用dp[i][j-v[i]]+w[i]这个状态的时候，我们需要判断下这个状态是否存在            if(dp[j-v[i]]!=-1)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);//我们这里是完全背包，所以我们这里是dp[i]的,我们这里就是选择i位置的，选多少个i位置的物品，那么总体归纳起来就是dp[i][j-v[i]]+w[i]        }    }    //我们输出结果的时候是不能进行直接输出的，我们是需要进行判断操作的    cout<<(dp[V]==-1?0:dp[V])<<endl;     return 0;}

可以对比，在空间优化方面，01背包和完全背包就内层for循环不一样

其实还有一个优化的点
我们在循环中加上这么一个状态就是想让后面的那个状态不生效，必须满足条件才能生效
只有合法才能进行使用

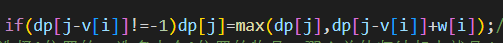
只要我们后面的那个状态足够小的话，那么我们就可以不加后面的那个状态以及前面的判断

这里的话我们是将无效的状态设置为-1，那么我们这里可以设置为无穷小（0x3f3f3f3f），那么我们就可以不用加这些判断条件了，
改动代码如下：返回值和判断条件改动了

#include #includeusing namespace std; const int N=1010; int n,V,v[N],w[N];int dp[N];int main(){    //读入数据    cin>>n>>V;    for(int i=1;i>v[i]>>w[i];    }     //解决第一问    //这里我们是不需要进行初始化操作的    for(int i=1;i<=n;i++)    {        for(int j=v[i];j=0)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);//我们这里是完全背包，所以我们这里是dp[i]的,我们这里就是选择i位置的，选多少个i位置的物品，那么总体归纳起来就是dp[i][j-v[i]]+w[i]        }    }    cout<<dp[V]<<endl;     //我们现在需要重新用dp表，所以需要将这个进行清空的操作    memset(dp,0,sizeof dp);    //初始化，我们需要将第一行除了第一个位置都初始化为-1，-1这个状态表示的就是这个位置是不能凑到j-v[i]的，就是不行的    for(int i=1;i<=V;i++)dp[i]=-0x3f3f3f3f;//都初始化为-1     for(int i=1;i<=n;i++)    {        for(int j=v[i];j<=V;j++)//我们从0开始进行计数，因为我们是没有初始化第一列的        {            //这里的话我们因为需要恰好凑到j，所以我们在使用dp[i][j-v[i]]+w[i]这个状态的时候，我们需要判断下这个状态是否存在            dp[j]=max(dp[j],dp[j-v[i]]+w[i]);//我们这里是完全背包，所以我们这里是dp[i]的,我们这里就是选择i位置的，选多少个i位置的物品，那么总体归纳起来就是dp[i][j-v[i]]+w[i]        }    }    //我们输出结果的时候是不能进行直接输出的，我们是需要进行判断操作的    cout<<(dp[V]<0?0:dp[V])<<endl;     return 0;}

54.零钱兑换

零钱兑换
给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入： coins = [1, 2, 5], amount = 11
输出：3
解释： 11 = 5 + 5 + 1

示例 2：

输入： coins = [2], amount = 3
输出：-1

示例 3：

输入： coins = [1], amount = 0
输出： 0

dp[i] [j]表示：从前i个硬币中挑选，总和正好等于j，所有的选法中的最少的硬币个数
因为这里我们需要满足总和正好等于j的情况，所以的话我们是需要初始化一种情况来表示这种选法是不合规的
我们直接将第一行从第二个格子开始初始化为无穷大就行了 0x3f3f3f3f
我们这里是求最少的硬币个数，就是最小值了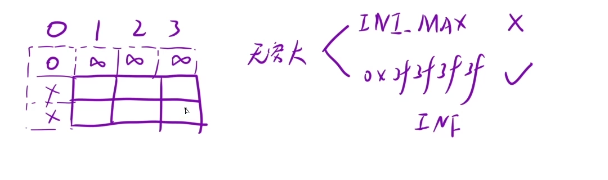
返回值，避免了无效的dp

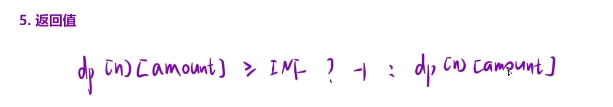
class Solution{public:    int coinChange(vector& coins, int amount)    {        const int INF=0x3f3f3f3f;        int n=coins.size();        vector<vector>dp(n+1,vector(amount+1));        //初始化的话，从第一个第二个格子开始都初始化为无穷大就行了        for(int i=1;i<=amount;i++)dp[0][i]=INF;         for(int i=1;i<=n;i++)        {            for(int j=0;j=0)dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1);//因为我们加了一行和一列，所以下标映射的时候是需要进行-1操作的            }        }        return (dp[n][amount]>=INF?-1:dp[n][amount]);//如果这个dp状态大于INF的话，那么就返回-1，如果不是的话那么就直接返回dp[n][amount]    }};

下面是空间优化的代码，将横坐标删除了

class Solution{public:    int coinChange(vector& coins, int amount)    {        const int INF=0x3f3f3f3f;        int n=coins.size();        vectordp(amount+1);        //初始化的话，从第一个第二个格子开始都初始化为无穷大就行了        for(int i=1;i<=amount;i++)dp[i]=INF;         for(int i=1;i<=n;i++)        {            for(int j=coins[i-1];j=INF?-1:dp[amount]);//如果这个dp状态大于INF的话，那么就返回-1，如果不是的话那么就直接返回dp[n][amount]    }};

55.零钱兑换 II

零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入： amount = 5, coins = [1, 2, 5]
输出： 4
解释： 有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

输入： amount = 3, coins = [2]
输出： 0
解释： 只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入： amount = 10, coins = [10]
输出： 1

提示：

• 1 <= coins.length <= 300
• 1 <= coins[i] <= 5000
• coins 中的所有值 互不相同
• 0 <= amount <= 5000

dp[i] [j]表示：从前i个物品中挑选，总体积不超过j，所有选法中，最大的价值

上面是固定的思路

下面是我们这道题的
dp[i] [j]表示：从前i个硬币中挑选，总和正好等于j，一共有多少种选法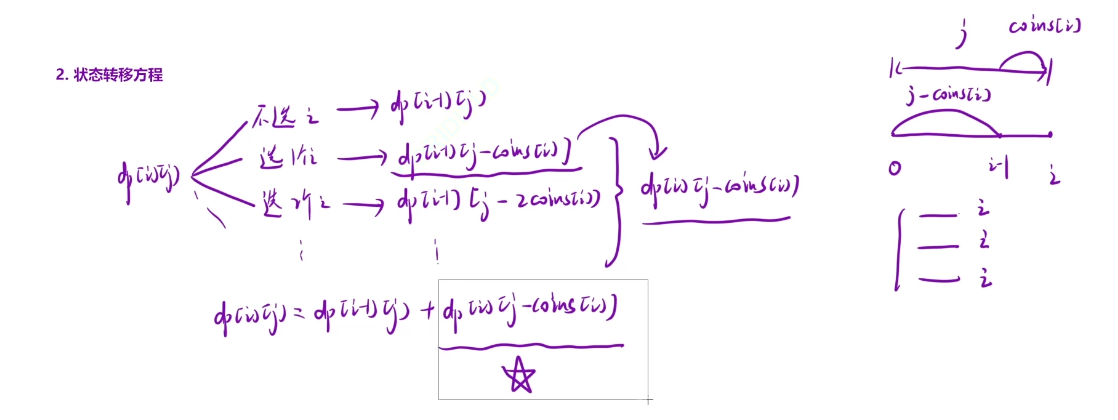
我们初始化的话就是直接将第一行的第一个格子初始化为1就行了，其他的都初始化为0

class Solution{public:    int change(int amount, vector& coins)    {        int n = coins.size();        vector dp(amount + 1, 0);  // 初始化 dp 数组，并将所有值设为 0        dp[0] = 1;  // 组合金额为 0 时，只有 1 种方式（即不选任何硬币）        for (int i = 0; i < n; i++)  // 遍历每个硬币        {            for (int j = coins[i]; j <= amount; j++)  // 从当前硬币的面值开始，更新 dp 数组            {                dp[j] += dp[j - coins[i]];  // 更新组合数            }        }        return dp[amount];  // 返回组合成目标金额 amount 的方案数    }};

这里的话我们是需要将dp表用double类型进行存储的，不然的话数据太大是会出现报错的

这里的代码我们直接展示空间优化后的代码的，就是删除了横坐标后的

55.完全平方数

完全平方数
给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入： n = 12
输出： 3
解释：12 = 4 + 4 + 4

示例 2：

输入： n = 13
输出： 2
解释：13 = 4 + 9

让我们在一堆数中挑几个数，然后达到我们的总和
并且一个数是可以挑好几次的

所以这个题的话就满足了完全背包的问题

dp[i] [j]表示：从前i个物品中挑选，总体积不超过j，所有选法中，最大的价值

那么我们这个题的即是
dp[i] [j]：从前i个完全平方数中挑选，总和正好等于i，所有选法中，最小的数量

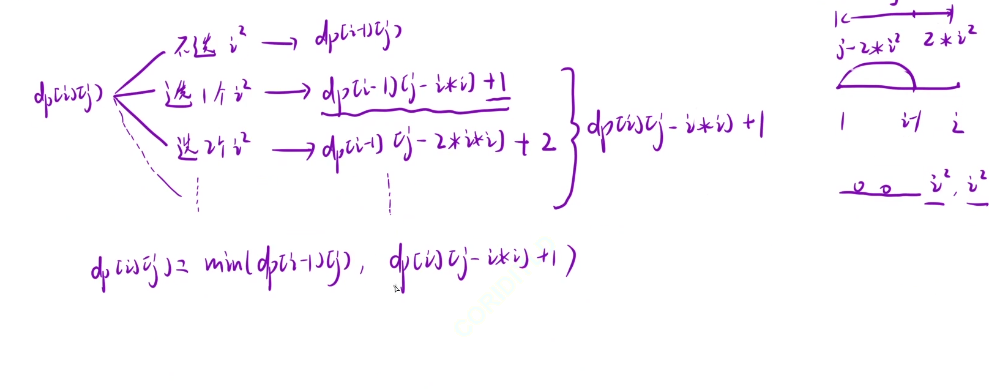
因为我们是需要使用到min求出最小的数量的，所以我们初始化的时候第一行的第一个格子初始化为0，其他的都初始化为无穷大，让他们不满足要求的参与不了这个比较

返回值的话如下：
因为如果给到我们的是13的话，那么我们只需要x^2<13

class Solution {public:    int numSquares(int n)    {        int m=sqrt(n);//根号n的结果        vector<vector>dp(m+1,vector(n+1));//规模就是根号n+1,m+1         //初始化        //除了第一个位置其他都初始化为无穷大        for(int i=1;i<=n;i++)dp[0][i]=0x3f3f3f3f;//初始化为无穷大就行了，不参与最小值比较        for(int i=1;i<=m;i++)        {            for(int j=1;j=i*i)dp[i][j]=min(dp[i][j],dp[i][j-i*i]+1);            }        }        return dp[m][n];    }};

接下来我们进行空间优化操作

class Solution {public:    int numSquares(int n)    {        int m=sqrt(n);//根号n的结果        vectordp(n+1);//规模就是根号n+1,m+1         //初始化        //除了第一个位置其他都初始化为无穷大        for(int i=1;i<=n;i++)dp[i]=0x3f3f3f3f;//初始化为无穷大就行了，不参与最小值比较        for(int i=1;i<=m;i++)        {            for(int j=i*i;j<=n;j++)            {                dp[j]=min(dp[j],dp[j-i*i]+1);            }        }        return dp[n];    }};