《LeetCode 动态规划 (进阶版)》整整 50 题量大管饱题解套餐 正在更新

1、动态规划 - 一维

Q1、最长字符串链

1、题目描述

给出一个单词数组 words ，其中每个单词都由小写英文字母组成。

如果我们可以 不改变其他字符的顺序 ，在 wordA 的任何地方添加 恰好一个 字母使其变成 wordB ，那么我们认为 wordA 是 wordB 的 前身 。

• 例如，\"abc\" 是 \"abac\" 的 前身 ，而 \"cba\" 不是 \"bcad\" 的 前身

词链是单词 [word_1, word_2, ..., word_k] 组成的序列，k >= 1，其中 word1 是 word2 的前身，word2 是 word3 的前身，依此类推。一个单词通常是 k == 1 的 单词链 。

从给定单词列表 words 中选择单词组成词链，返回 词链的 最长可能长度 。

示例 1：

输入：words = [\"a\",\"b\",\"ba\",\"bca\",\"bda\",\"bdca\"]输出：4解释：最长单词链之一为 [\"a\",\"ba\",\"bda\",\"bdca\"]

示例 2:

输入：words = [\"xbc\",\"pcxbcf\",\"xb\",\"cxbc\",\"pcxbc\"]输出：5解释：所有的单词都可以放入单词链 [\"xb\", \"xbc\", \"cxbc\", \"pcxbc\", \"pcxbcf\"].

示例 3:

输入：words = [\"abcd\",\"dbqca\"]输出：1解释：字链[\"abcd\"]是最长的字链之一。[\"abcd\"，\"dbqca\"]不是一个有效的单词链，因为字母的顺序被改变了。

提示：

• 1 <= words.length <= 1000
• 1 <= words[i].length <= 16
• words[i] 仅由小写英文字母组成。

2、解题思路

动态规划法

1. 排序：首先将单词按长度排序，便于处理前身关系
2. 哈希表记录：使用哈希表记录每个单词的最长链长度
3. 动态更新 ：
   • 对于每个单词，尝试删除一个字符，检查是否存在前身
   • 如果存在，更新当前单词的最长链长度
4. 维护最大值：在遍历过程中维护全局最长链长度

3、代码实现

C++

class Solution {public: int longestStrChain(vector& words) { // 使用哈希表记录每个单词对应的最长链长度 unordered_map dp; // 按照单词长度排序, 短单词在前 // 这样处理时, 当前单词的前身一定已经被处理过 sort(words.begin(), words.end(), [](const string& a, const string& b) { return a.size() < b.size(); }); int max_length = 0; // 记录全局最长链长度 for (const string& word : words) { // 初始化当前单词的最长链长度为 1 (单独作为一个链) dp[word] = 1; // 尝试删除当前单词的每一个字符, 检查是否存在前身 for (int i = 0; i < word.size(); ++i) { // 生成可能的 \"前身\" 单词 string predecessor = word.substr(0, i) + word.substr(i + 1); // 如果这个前身存在于哈希表中 if (dp.count(predecessor)) {  // 更新当前单词的最长链长度  // 当前长度可能是自身长度, 或是前身长度 +1 中的较大值  dp[word] = max(dp[word], dp[predecessor] + 1); } } // 更新全局最长链长度 max_length = max(max_length, dp[word]); } return max_length; }};

Java

class Solution { public int longestStrChain(String[] words) { // 按照单词长度排序 Arrays.sort(words, (a, b) -> a.length() - b.length()); Map<String, Integer> dp = new HashMap<>(); int maxLen = 1; for (String word : words) { dp.put(word, 1); // 每个单词至少可以单独成链 // 尝试删除每个位置的字符，寻找前身 for (int i = 0; i < word.length(); i++) { String predecessor = word.substring(0, i) + word.substring(i + 1); if (dp.containsKey(predecessor)) {  dp.put(word, Math.max(dp.get(word), dp.get(predecessor) + 1)); } } maxLen = Math.max(maxLen, dp.get(word)); } return maxLen; }}

Python

class Solution: def longestStrChain(self, words: List[str]) -> int: # 按照单词长度排序 words.sort(key=len) dp = {} max_len = 1 for word in words: dp[word] = 1 # 每个单词至少可以单独成链 # 尝试删除每个位置的字符，寻找前身 for i in range(len(word)): predecessor = word[:i] + word[i+1:] if predecessor in dp:  dp[word] = max(dp[word], dp[predecessor] + 1) max_len = max(max_len, dp[word]) return max_len

4、复杂度分析

• 时间复杂度：O(N*L²)，其中N是单词数量，L是单词平均长度
• 空间复杂度：O(N)，用于存储哈希表

Q2、摆动序列

1、题目描述

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 **摆动序列 。**第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

• 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]输出：6解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]输出：7解释：这个序列包含几个长度为 7 摆动序列。其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]输出：2

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

**进阶：**你能否用 O(n) 时间复杂度完成此题?

2、解题思路

方法一：动态规划

1. 定义两个状态数组 up 和 down ：
   • up[i]表示以nums[i]结尾且最后差为正的最长摆动序列长度
   • down[i]表示以nums[i]结尾且最后差为负的最长摆动序列长度
2. 状态转移：
   • 如果nums[i] > nums[i-1]，可以从前一个下降序列转移过来
   • 如果nums[i] < nums[i-1]，可以从前一个上升序列转移过来
3. 时间复杂度：O(n)，空间复杂度：O(n)

方法二：优化空间动态规划

1. 观察到只需要前一个状态，可以优化空间复杂度
2. 只需维护两个变量up和down
3. 时间复杂度：O(n)，空间复杂度：O(1)

方法三：贪心算法

1. 统计实际摆动次数
2. 维护前一个差值和当前差值
3. 当摆动方向发生变化时计数
4. 时间复杂度：O(n)，空间复杂度：O(1)

3、代码实现

C++

// 方法1: 动态规划class Solution {public: int wiggleMaxLength(vector& nums) { int n = nums.size(); if (n < 2) { return n; // 长度小于 2 直接返回 } // up[i] 表示以 nums[i] 结尾且最后差为正的最长摆动序列长度 // down[i] 表示以 nums[i] 结尾且最后差为负的最长摆动序列长度 vector up(n, 1), down(n, 1); for (int i = 1; i  nums[i - 1]) // 当前上升 { up[i] = down[i - 1] + 1; // 可以从下降转移过来 down[i] = down[i - 1]; // 下降序列保持不变 } else if (nums[i] < nums[i - 1]) // 当前下降 { down[i] = up[i - 1] + 1; // 可以从上升转移过来 up[i] = up[i - 1]; // 上升序列保持不变 } else // 相等情况 { up[i] = up[i - 1]; down[i] = down[i - 1]; } } return max(up.back(), down.back()); }};

// 方法2: 动态规划空间优化class Solution {public: int wiggleMaxLength(vector& nums) { int n = nums.size(); if (n < 2) { return n; } int up = 1, down = 1; // 只需要维护前一个状态 for (int i = 1; i  nums[i - 1]) { up = down + 1; // 从下降转移过来 } else if (nums[i] < nums[i - 1]) { down = up + 1; // 从上升转移过来 } // 相等情况不做处理 } return max(up, down); }};

// 方法3: 贪心算法class Solution {public: int wiggleMaxLength(vector& nums) { int n = nums.size(); if (n < 2) { return n; } int prevDiff = nums[1] - nums[0]; int count = prevDiff != 0 ? 2 : 1; // 初始计数 for (int i = 2; i  0 && prevDiff <= 0) || (diff = 0)) { count++; prevDiff = diff; // 只在摆动方向变化时更新 prevDiff } } return count; }};

Java

// 方法1: 动态规划class Solution { public int wiggleMaxLength(int[] nums) { int n = nums.length; if (n < 2) { return n; } int[] up = new int[n]; int[] down = new int[n]; up[0] = down[0] = 1; for (int i = 1; i < n; i++) { if (nums[i] > nums[i - 1]) { up[i] = down[i - 1] + 1; down[i] = down[i - 1]; } else if (nums[i] < nums[i - 1]) { down[i] = up[i - 1] + 1; up[i] = up[i - 1]; } else { up[i] = up[i - 1]; down[i] = down[i - 1]; } } return Math.max(up[n - 1], down[n - 1]); }}

// 方法2: 动态规划空间优化class Solution { public int wiggleMaxLength(int[] nums) { int n = nums.length; if (n < 2) { return n; } int up = 1, down = 1; for (int i = 1; i < n; i++) { if (nums[i] > nums[i - 1]) { up = down + 1; } else if (nums[i] < nums[i - 1]) { down = up + 1; } } return Math.max(up, down); }}

// 方法3: 贪心算法class Solution { public int wiggleMaxLength(int[] nums) { int n = nums.length; if (n < 2) { return n; } int prevDiff = nums[1] - nums[0]; int count = prevDiff != 0 ? 2 : 1; for (int i = 2; i < n; i++) { int diff = nums[i] - nums[i - 1]; if ((diff > 0 && prevDiff <= 0) || (diff < 0 && prevDiff >= 0)) { count++; prevDiff = diff; } } return count; }}

Python

// 方法1: 动态规划class Solution: def wiggleMaxLength(self, nums: List[int]) -> int: n = len(nums) if n < 2: return n up = [1] * n # up[i]表示以nums[i]结尾且最后差为正的最长摆动序列长度 down = [1] * n # down[i]表示以nums[i]结尾且最后差为负的最长摆动序列长度 for i in range(1, n): if nums[i] > nums[i-1]: up[i] = down[i-1] + 1 down[i] = down[i-1] elif nums[i] < nums[i-1]: down[i] = up[i-1] + 1 up[i] = up[i-1] else: up[i] = up[i-1] down[i] = down[i-1] return max(up[-1], down[-1])

// 方法2: 动态规划空间优化class Solution: def wiggleMaxLength(self, nums: List[int]) -> int: n = len(nums) if n < 2: return n up = down = 1 for i in range(1, n): if nums[i] > nums[i-1]: up = down + 1 elif nums[i] < nums[i-1]: down = up + 1 return max(up, down)

// 方法3: 贪心算法class Solution: def wiggleMaxLength(self, nums: List[int]) -> int: n = len(nums) if n < 2: return n prev_diff = nums[1] - nums[0] count = 2 if prev_diff != 0 else 1 for i in range(2, n): diff = nums[i] - nums[i-1] if (diff > 0 and prev_diff <= 0) or (diff < 0 and prev_diff >= 0): count += 1 prev_diff = diff return count

4、复杂度分析

三种方法的时间复杂度均为O(n)，其中n是数组长度：

• 方法一空间复杂度O(n)，使用了两个数组
• 方法二和方法三空间复杂度O(1)，只使用了常数个变量

Q3、四个键的键盘

1、题目描述

假设你有一个特殊的键盘包含下面的按键：

• A：在屏幕上打印一个 \'A\'。
• Ctrl-A：选中整个屏幕。
• Ctrl-C：复制选中区域到缓冲区。
• Ctrl-V：将缓冲区内容输出到上次输入的结束位置，并显示在屏幕上。

现在，你可以 最多 按键 n 次（使用上述四种按键），返回屏幕上最多可以显示 \'A\' 的个数 。

示例 1:

输入: n = 3输出: 3解释: 我们最多可以在屏幕上显示三个\'A\'通过如下顺序按键：A, A, A

示例 2:

输入: n = 7输出: 9解释: 我们最多可以在屏幕上显示九个\'A\'通过如下顺序按键：A, A, A, Ctrl A, Ctrl C, Ctrl V, Ctrl V

提示:

• 1 <= n <= 50

2、解题思路

方法一：动态规划

1. 状态定义：best[k]表示按键k次能获得的最大A数
2. 基本情况：best[1] = 1（按一次A）
3. 状态转移 ：
   • 直接按A：best[k] = best[k-1] + 1
   • 使用复制粘贴：尝试在x次操作后进行全选-复制-多次粘贴操作
4. 时间复杂度：O(n²)，空间复杂度：O(n)

方法二：数学规律（打表法）

1. 观察规律：发现当n较大时，最优解遵循特定模式
2. 预先计算：存储小规模的解，大规模问题通过数学公式推导
3. 时间复杂度：O(1)，空间复杂度：O(1)（使用固定大小的表）

3、代码实现

C++

// 方法1: 动态规划class Solution {public: int maxA(int n) { vector best(n + 1, 0); // best[k] 表示 k 次操作后的最大值 for (int k = 1; k <= n; ++k) { // 情况1: 最后一次按 A 键 best[k] = best[k - 1] + 1; // 情况2: 尝试在 x 次操作后, 按 Ctrl-A, Ctrl-C, 然后多次 Ctrl-v for (int x = 0; x < k - 1; ++x) { // x 次操作获得 best[x] 个 A // 然后需要按 Ctrl-A(x次), Ctrl-C(1次), 剩下 k-x-1 次 Ctrl-V best[k] = max(best[k], best[x] * (k - x - 1)); } } return best[n]; }};

// 方法2: 数学规律class Solution {public: int maxA(int n) { // 预先计算好的小规模解 const int best[] = {0, 1, 2, 3, 4, 5, 6, 9, 12, 16, 20, 27, 36, 48, 64, 81}; if (n 15 的情况, 使用数学规律 int q = (n - 11) / 5;  // 计算需要乘以 4 的 q 次方 return best[n - 5 * q] * (1 << (2 * q)); // 4^q = 2^(2q) }};

Java

class Solution { public int maxA(int n) { int[] best = new int[n + 1]; // best[k]表示k次操作后的最大值 for (int k = 1; k <= n; ++k) { // 情况1：最后一次按A键 best[k] = best[k - 1] + 1; // 情况2：尝试在x次操作后，按Ctrl-A,Ctrl-C,然后多次Ctrl-V for (int x = 0; x < k - 1; ++x) { best[k] = Math.max(best[k], best[x] * (k - x - 1)); } } return best[n]; }}

class Solution { public int maxA(int n) { // 预先计算好的小规模解 int[] best = { 0, 1, 2, 3, 4, 5, 6, 9, 12, 16, 20, 27, 36, 48, 64, 81 }; if (n <= 15) { return best[n]; } // 对于n>15的情况，使用数学规律 int q = (n - 11) / 5; // 计算需要乘以4的q次方 return best[n - 5 * q] * (1 << (2 * q)); // 4^q = 2^(2q) }}

Python

class Solution: def maxA(self, n: int) -> int: best = [0] * (n + 1) # best[k]表示k次操作后的最大值 for k in range(1, n + 1): # 情况1：最后一次按A键 best[k] = best[k-1] + 1 # 情况2：尝试在x次操作后，按Ctrl-A,Ctrl-C,然后多次Ctrl-V for x in range(k-1): best[k] = max(best[k], best[x] * (k - x - 1)) return best[n]

class Solution: def maxA(self, n: int) -> int: # 预先计算好的小规模解 best = [0, 1, 2, 3, 4, 5, 6, 9, 12,  16, 20, 27, 36, 48, 64, 81] if n <= 15: return best[n] # 对于n>15的情况，使用数学规律 q = (n - 11) // 5 # 计算需要乘以4的q次方 return best[n - 5*q] * (4 ** q)

4、复杂度分析

方法一：动态规划

• 时间复杂度：O(n²)，因为有两层嵌套循环
• 空间复杂度：O(n)，用于存储dp数组

方法二：数学规律

• 时间复杂度：O(1)，只需要查表和简单计算
• 空间复杂度：O(1)，使用固定大小的表

Q4、最长有效括号

1、题目描述

给你一个只包含 \'(\' 和 \')\' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

输入：s = \"(()\"输出：2解释：最长有效括号子串是 \"()\"

示例 2：

输入：s = \")()())\"输出：4解释：最长有效括号子串是 \"()()\"

示例 3：

输入：s = \"\"输出：0

提示：

• 0 <= s.length <= 3 * 104
• s[i] 为 \'(\' 或 \')\'

2、解题思路

方法一：动态规划

1. 定义状态：dp[i]表示以s[i]结尾的最长有效括号子串长度
2. 状态转移 ：
   • s[i]=‘)‘且s[i-1]=’(’：dp[i] = dp[i-2] + 2
   • s[i]=‘)‘且s[i-1]=’)’：检查前面是否有匹配的’(’
3. 初始化：dp数组初始化为0
4. 结果：dp数组中的最大值

方法二：栈

1. 使用栈：栈底始终保存最后一个不能匹配的’)\'的位置
2. 遍历字符串 ：
   • ‘(’：压栈
   • ‘)’：弹出栈顶，计算当前有效长度
3. 结果：记录过程中的最大长度

方法三：双向遍历

1. 从左到右：统计左右括号数量，相等时更新最大值
2. 从右到左：同上，处理左括号多的情况
3. 结果：两次遍历中的最大值

3、代码实现

C++

// 方法1: 动态规划class Solution {public: int longestValidParentheses(string s) { int n = s.size(), max_len = 0; vector dp(n, 0); // dp[i] 表示以 s[i] 结尾的最长有效括号长度 for (int i = 1; i = 2 ? dp[i - 2] : 0) + 2; } else if (i - dp[i - 1] > 0 && s[i - dp[i - 1] - 1] == \'(\') {  // 形如 \"...((...))\"  dp[i] = dp[i - 1] + ((i - dp[i - 1] - 2) >= 0 ? dp[i - dp[i - 1] - 2] : 0) + 2; } max_len = max(max_len, dp[i]); } } return max_len; }};

// 方法2: 栈方法class Solution {public: int longestValidParentheses(string s) { stack stk; stk.push(-1); // 初始基准位置 int max_len = 0; for (int i = 0; i < s.size(); ++i) { if (s[i] == \'(\') { stk.push(i); } else { stk.pop(); if (stk.empty()) {  stk.push(i); // 更新基准位置 } else {  max_len = max(max_len, i - stk.top()); } } } return max_len; }};

// 方法3: 双向遍历class Solution {public: int longestValidParentheses(string s) { int left = 0, right = 0, max_len = 0; // 从左到右遍历 for (char c : s) { if (c == \'(\') { left++; } else { right++; } if (left == right) { max_len = max(max_len, 2 * right); } else if (right > left) { left = right = 0; } } left = right = 0; // 从右向左遍历 for (int i = s.size() - 1; i >= 0; --i) { if (s[i] == \'(\') { left++; } else { right++; } if (left == right) { max_len = max(max_len, 2 * left); } else if (left > right) { left = right = 0; } } return max_len; }};

Java

class Solution { public int longestValidParentheses(String s) { Stack<Integer> stack = new Stack<>(); stack.push(-1); int maxLen = 0; for (int i = 0; i < s.length(); i++) { if (s.charAt(i) == \'(\') { stack.push(i); } else { stack.pop(); if (stack.isEmpty()) {  stack.push(i); } else {  maxLen = Math.max(maxLen, i - stack.peek()); } } } return maxLen; }}

Python

class Solution: def longestValidParentheses(self, s: str) -> int: left = right = max_len = 0 # Left to right pass for c in s: if c == \'(\': left += 1 else: right += 1 if left == right: max_len = max(max_len, 2 * right) elif right > left: left = right = 0 left = right = 0 # Right to left pass for c in reversed(s): if c == \'(\': left += 1 else: right += 1 if left == right: max_len = max(max_len, 2 * left) elif left > right: left = right = 0 return max_len

4、复杂度分析

• 动态规划：时间复杂度O(n)，空间复杂度O(n)
• 栈方法：时间复杂度O(n)，空间复杂度O(n)
• 双向遍历：时间复杂度O(n)，空间复杂度O(1)

Q5、恢复数组

1、题目描述

某个程序本来应该输出一个整数数组。但是这个程序忘记输出空格了以致输出了一个数字字符串，我们所知道的信息只有：数组中所有整数都在 [1, k] 之间，且数组中的数字都没有前导 0 。

给你字符串 s 和整数 k 。可能会有多种不同的数组恢复结果。

按照上述程序，请你返回所有可能输出字符串 s 的数组方案数。

由于数组方案数可能会很大，请你返回它对 10^9 + 7 取余 后的结果。

示例 1：

输入：s = \"1000\", k = 10000输出：1解释：唯一一种可能的数组方案是 [1000]

示例 2：

输入：s = \"1000\", k = 10输出：0解释：不存在任何数组方案满足所有整数都 >= 1 且 <= 10 同时输出结果为 s 。

示例 3：

输入：s = \"1317\", k = 2000输出：8解释：可行的数组方案为 [1317]，[131,7]，[13,17]，[1,317]，[13,1,7]，[1,31,7]，[1,3,17]，[1,3,1,7]

示例 4：

输入：s = \"2020\", k = 30输出：1解释：唯一可能的数组方案是 [20,20] 。 [2020] 不是可行的数组方案，原因是 2020 > 30 。 [2,020] 也不是可行的数组方案，因为 020 含有前导 0 。

示例 5：

输入：s = \"1234567890\", k = 90输出：34

提示：

• 1 <= s.length <= 10^5.
• s 只包含数字且不包含前导 0 。
• 1 <= k <= 10^9.

2、解题思路

动态规划方法

1. 状态定义：f[i]表示前i个字符的分割方案数
2. 初始状态：f[0] = 1（空字符串有一种分割方式）
3. 状态转移 ：
   • 从i-1向前查看最多10位（因为k最多10^9，最多10位数字）
   • 检查当前数字是否在[1, k]范围内且无前导零
   • 累加所有有效分割点的方案数
4. 优化：由于k最多10^9，只需检查最多10位数字即可

3、代码实现

C++

class Solution {private: static constexpr int mod = 1000000007;public: int numberOfArrays(string s, int k) { int n = s.size(); long long kll = k; // 转换成 long long 防止溢出 vector f(n + 1, 0); f[0] = 1; // 空字符串有一种分割方式 for (int i = 1; i = 0 && i - j  kll) {  break; // 超过 k 直接终止 } // 检查是否有前导零 (s[j] 不能是 \'0\') if (s[j] != \'0\') {  f[i] = (f[i] + f[j]) % mod; } base *= 10; // 每次左移一位 } } return f[n]; }};

Java

class Solution { private static final int MOD = 1000000007; public int numberOfArrays(String s, int k) { int n = s.length(); long kLong = k; // 转换为long防止溢出 int[] f = new int[n + 1]; f[0] = 1; // 空字符串有一种分割方式 for (int i = 1; i <= n; ++i) { long num = 0, base = 1; // 从 i-1 向前看最多 10 位 for (int j = i - 1; j >= 0 && i - j <= 10; --j) { num += (s.charAt(j) - \'0\') * base; // 计算数字值 if (num > kLong)  break; // 超过 k 直接终止 // 检查是否有前导零 if (s.charAt(j) != \'0\') {  f[i] = (f[i] + f[j]) % MOD; } base *= 10; // 每次左移一位 } } return f[n]; }}

Python

class Solution: def numberOfArrays(self, s: str, k: int) -> int: MOD = 10**9 + 7 n = len(s) f = [0] * (n + 1) f[0] = 1 # 空字符串有一种分割方式 for i in range(1, n + 1): num = 0 base = 1 # 从i-1向前看最多10位 for j in range(i - 1, max(-1, i - 11) - 1, -1): num += (ord(s[j]) - ord(\"0\")) * base # 计算数字值 if num > k:  break # 超过k直接终止 # 检查是否有前导零 if s[j] != \"0\":  f[i] = (f[i] + f[j]) % MOD base *= 10 # 每次左移一位 return f[n]

4、复杂度分析

• 时间复杂度：O(n*10)=O(n)，因为每个字符最多检查10次
• 空间复杂度：O(n)，用于存储dp数组

Q6、不相交的握手

1、题目描述

偶数 个人站成一个圆，总人数为 num_people 。每个人与除自己外的一个人握手，所以总共会有 num_people / 2 次握手。

将握手的人之间连线，请你返回连线不会相交的握手方案数。

由于结果可能会很大，请你返回答案 模 10^9+7 后的结果。

示例 1：

输入：num_people = 2输出：1

示例 2：

输入：num_people = 4输出：2解释：总共有两种方案，第一种方案是 [(1,2),(3,4)] ，第二种方案是 [(2,3),(4,1)] 。

示例 3：

输入：num_people = 6输出：5

示例 4：

输入：num_people = 8输出：14

提示：

• 2 <= num_people <= 1000
• num_people % 2 == 0

2、解题思路

动态规划方法

1. 状态定义：dp[i]表示2i个人不相交握手的方案数
2. 初始状态 ：
   • dp[0] = 1（0个人有1种方案）
   • dp[1] = 1（2个人只有1种握手方式）
3. 状态转移 ：
   • 当固定一个人（比如1号）与另一个人（比如k号）握手时，圆圈被分成两部分
   • 左边部分有k-2个人，右边部分有num_people-k个人
   • 这两部分的人数都必须是偶数（因为每次握手减少2人）
   • 方案数为所有可能分割方式的乘积之和
4. 数学基础：这是卡塔兰数的应用，方案数为第n/2个卡塔兰数

3、代码实现

C++

class Solution {public: int numberOfWays(int numPeople) { const int MOD = 1000000007; // 模数，防止结果过大 int numPairs = numPeople / 2; // 计算握手对数 // 特殊情况处理 if (numPairs == 1) { return 1; // 只有2个人的情况 } // dp数组: dp[i] 表示 2i 个人不相交握手的方案数 vector dp(numPairs + 1, 0); // 基础情况 dp[0] = 1; // 0个人的情况（空方案） dp[1] = 1; // 2个人的情况（只有1种握手方式） // 动态规划填表 for (int i = 2; i <= numPairs; ++i) { // 计算 dp[i]: 考虑所有可能的分割方式 for (int j = 0; j < i; ++j) { // dp[i] = sum(dp[j] * dp[i-j-1]) for j from 0 to i-1 // j 表示左边部分的握手对数 // i-j-1 表示右边部分的握手对数 dp[i] = (dp[i] + dp[j] * dp[i - j - 1]) % MOD; } } return static_cast(dp[numPairs] % MOD); }};

Java

class Solution { private static final int MOD = 1000000007; // 模数定义为常量 public int numberOfWays(int numPeople) { int numPairs = numPeople / 2; // 计算握手对数 // 特殊情况处理 if (numPairs == 1) { return 1; // 只有2个人 } // dp数组：dp[i]表示2i个人不相交握手的方案数 long[] dp = new long[numPairs + 1]; // 基础情况 dp[0] = 1; // 0个人 dp[1] = 1; // 2个人 // 动态规划填表 for (int i = 2; i <= numPairs; i++) { // 计算dp[i]：考虑所有可能的分割方式 for (int j = 0; j < i; j++) { // dp[i] = sum(dp[j] * dp[i-j-1]) for j from 0 to i-1 dp[i] = (dp[i] + dp[j] * dp[i - j - 1]) % MOD; } } return (int) (dp[numPairs] % MOD); }}

Python

class Solution: def numberOfWays(self, numPeople: int) -> int: MOD = 10**9 + 7 # 模数 num_pairs = numPeople // 2 # 计算握手对数 # 特殊情况处理 if num_pairs == 1: return 1 # 只有2个人的情况 # dp数组：dp[i]表示2i个人不相交握手的方案数 dp = [0] * (num_pairs + 1) # 基础情况 dp[0] = 1 # 0个人的情况（空方案） dp[1] = 1 # 2个人的情况（只有1种握手方式） # 动态规划填表 for i in range(2, num_pairs + 1): # 计算dp[i]：考虑所有可能的分割方式 for j in range(i): # dp[i] = sum(dp[j] * dp[i-j-1]) for j from 0 to i-1 dp[i] = (dp[i] + dp[j] * dp[i - j - 1]) % MOD return dp[num_pairs] % MOD

4、复杂度分析

• 时间复杂度：O(n²)，因为有两层循环
• 空间复杂度：O(n)，用于存储dp数组

Q7、解码方法 II

1、题目描述

一条包含字母 A-Z 的消息通过以下的方式进行了 编码 ：

\'A\' -> \"1\"\'B\' -> \"2\"...\'Z\' -> \"26\"

要 解码 一条已编码的消息，所有的数字都必须分组，然后按原来的编码方案反向映射回字母（可能存在多种方式）。例如，\"11106\" 可以映射为：

• \"AAJF\" 对应分组 (1 1 10 6)
• \"KJF\" 对应分组 (11 10 6)

注意，像 (1 11 06) 这样的分组是无效的，因为 \"06\" 不可以映射为 \'F\' ，因为 \"6\" 与 \"06\" 不同。

除了 上面描述的数字字母映射方案，编码消息中可能包含 \'*\' 字符，可以表示从 \'1\' 到 \'9\' 的任一数字（不包括 \'0\'）。例如，编码字符串 \"1*\" 可以表示 \"11\"、\"12\"、\"13\"、\"14\"、\"15\"、\"16\"、\"17\"、\"18\" 或 \"19\" 中的任意一条消息。对 \"1*\" 进行解码，相当于解码该字符串可以表示的任何编码消息。

给你一个字符串 s ，由数字和 \'*\' 字符组成，返回 解码 该字符串的方法 数目 。

由于答案数目可能非常大，返回 109 + 7 的 模 。

示例 1：

输入：s = \"*\"输出：9解释：这一条编码消息可以表示 \"1\"、\"2\"、\"3\"、\"4\"、\"5\"、\"6\"、\"7\"、\"8\" 或 \"9\" 中的任意一条。可以分别解码成字符串 \"A\"、\"B\"、\"C\"、\"D\"、\"E\"、\"F\"、\"G\"、\"H\" 和 \"I\" 。因此，\"*\" 总共有 9 种解码方法。

示例 2：

输入：s = \"1*\"输出：18解释：这一条编码消息可以表示 \"11\"、\"12\"、\"13\"、\"14\"、\"15\"、\"16\"、\"17\"、\"18\" 或 \"19\" 中的任意一条。每种消息都可以由 2 种方法解码（例如，\"11\" 可以解码成 \"AA\" 或 \"K\"）。因此，\"1*\" 共有 9 * 2 = 18 种解码方法。

示例 3：

输入：s = \"2*\"输出：15解释：这一条编码消息可以表示 \"21\"、\"22\"、\"23\"、\"24\"、\"25\"、\"26\"、\"27\"、\"28\" 或 \"29\" 中的任意一条。\"21\"、\"22\"、\"23\"、\"24\"、\"25\" 和 \"26\" 由 2 种解码方法，但 \"27\"、\"28\" 和 \"29\" 仅有 1 种解码方法。因此，\"2*\" 共有 (6 * 2) + (3 * 1) = 12 + 3 = 15 种解码方法。

提示：

• 1 <= s.length <= 105
• s[i] 是 0 - 9 中的一位数字或字符 \'*\'

2、解题思路

动态规划方法

1. 状态定义：使用三个变量a, b, c来代表状态：
   • a = f[i-2]（前两位置的解码方法数）
   • b = f[i-1]（前一位置的解码方法数）
   • c = f[i]（当前位置的解码方法数）
2. 辅助函数：
   • check1digit：检查单个字符的解码可能性
   • check2digits：检查两个字符组合的解码可能性
3. 状态转移：
   • 当前位置的解码方法数 = 单独解码当前字符的方法数 + 与前一个字符组合解码的方法数
   • 使用模运算防止溢出

3、代码实现

C++

class Solution {private: static constexpr int mod = 1000000007; // 定义模数public: int numDecodings(string s) { // 检查单个字符的解码可能性 auto check1digit = [](char ch) -> int { if (ch == \'0\') { return 0; // 0 不能单独解码 } return ch == \'*\' ? 9 : 1; // * 可以代表 1-9 共 9 种 }; // 检查两个字符组合的解码可能性 auto check2digit = [](char c0, char c1) -> int { if (c0 == \'*\' && c1 == \'*\') { // ** 可以组成 11-19, 21-26 共 15 种有效组合 return 15; } if (c0 == \'*\') { // *x: 当 x 6 时, 只有 1x 有效 (1种) return c1 <= \'6\' ? 2 : 1; } if (c1 == \'*\') { if (c0 == \'1\') {  return 9; // 1*: 11-19 共 9 种 } if (c0 == \'2\') {  return 6; // 2*: 21-26 共 6 种 } return 0; // 其他情况无效 } // 两个数字的情况 return c0 != \'0\' && (c0 - \'0\') * 10 + (c1 - \'0\') <= 26; }; int n = s.size(); // 使用滚动数组优化空间 // a = f[i-2], b = f[i-1], c = f[i] int a = 0, b = 1, c = 0; for (int i = 1; i  1) { c = (c + (long long)a * check2digit(s[i - 2], s[i - 1])) % mod; } // 滚动更新状态 a = b; b = c; } return c; }};

Java

class Solution { private static final int MOD = 1000000007; private int check1(char ch) { if (ch == \'0\') { return 0; } return ch == \'*\' ? 9 : 1; } private int check2(char c1, char c2) { if (c1 == \'*\' && c2 == \'*\') { return 15; } if (c1 == \'*\') { return (c2 <= \'6\') ? 2 : 1; } if (c2 == \'*\') { if (c1 == \'1\') { return 9; } if (c1 == \'2\') { return 6; } return 0; } int num = (c1 - \'0\') * 10 + (c2 - \'0\'); return (c1 != \'0\' && num >= 1 && num <= 26) ? 1 : 0; } public int numDecodings(String s) { int n = s.length(); long prev2 = 0, prev1 = 1, curr = 0; for (int i = 1; i <= n; i++) { curr = prev1 * check1(s.charAt(i - 1)) % MOD; if (i > 1) { curr = (curr + prev2 * check2(s.charAt(i - 2), s.charAt(i - 1))) % MOD; } prev2 = prev1; prev1 = curr; } return (int) curr; }}

Python

class Solution: def numDecodings(self, s: str) -> int: MOD = 10**9 + 7 def check1(ch): if ch == \'0\': return 0 return 9 if ch == \'*\' else 1 def check2(c1, c2): if c1 == \'*\' and c2 == \'*\': return 15 if c1 == \'*\': return 2 if c2 <= \'6\' else 1 if c2 == \'*\': if c1 == \'1\': return 9 if c1 == \'2\': return 6 return 0 num = int(c1) * 10 + int(c2) return 1 if c1 != \'0\' and 1 <= num <= 26 else 0 n = len(s) prev2, prev1, curr = 0, 1, 0 for i in range(1, n+1): curr = prev1 * check1(s[i-1]) % MOD if i > 1: curr = (curr + prev2 * check2(s[i-2], s[i-1])) % MOD prev2, prev1 = prev1, curr return curr

4、复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(1)（使用滚动数组优化）

2、动态规划 - 多维

Q8、执行乘法运算的最大分数

1、题目描述

给你两个长度分别 n 和 m 的整数数组 nums 和 multipliers ，其中 n >= m ，数组下标 从 1 开始 计数。

初始时，你的分数为 0 。你需要执行恰好 m 步操作。在第 i 步操作（从 1 开始 计数）中，需要：

• 选择数组 nums 开头处或者末尾处 的整数 x 。
• 你获得 multipliers[i] * x 分，并累加到你的分数中。
• 将 x 从数组 nums 中移除。

在执行 m 步操作后，返回 最大 分数*。*

示例 1：

输入：nums = [1,2,3], multipliers = [3,2,1]输出：14解释：一种最优解决方案如下：- 选择末尾处的整数 3 ，[1,2,3] ，得 3 * 3 = 9 分，累加到分数中。- 选择末尾处的整数 2 ，[1,2] ，得 2 * 2 = 4 分，累加到分数中。- 选择末尾处的整数 1 ，[1] ，得 1 * 1 = 1 分，累加到分数中。总分数为 9 + 4 + 1 = 14 。

示例 2：

输入：nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6]输出：102解释：一种最优解决方案如下：- 选择开头处的整数 -5 ，[-5,-3,-3,-2,7,1] ，得 -5 * -10 = 50 分，累加到分数中。- 选择开头处的整数 -3 ，[-3,-3,-2,7,1] ，得 -3 * -5 = 15 分，累加到分数中。- 选择开头处的整数 -3 ，[-3,-2,7,1] ，得 -3 * 3 = -9 分，累加到分数中。- 选择末尾处的整数 1 ，[-2,7,1] ，得 1 * 4 = 4 分，累加到分数中。- 选择末尾处的整数 7 ，[-2,7] ，得 7 * 6 = 42 分，累加到分数中。总分数为 50 + 15 - 9 + 4 + 42 = 102 。

提示：

• n == nums.length
• m == multipliers.length
• 1 <= m <= 103
• m <= n <= 105``
• -1000 <= nums[i], multipliers[i] <= 1000

2、解题思路

状态定义

使用二维 DP 数组 dp[i][j] 表示：从 nums 开头取了 i 个元素，从末尾取了 j 个元素时的最大分数。

状态转移

对于第 k 步操作（k = i + j）：

1. 如果从开头取元素：dp[i][j] = dp[i-1][j] + nums[i-1] * multipliers[k-1]
2. 如果从末尾取元素：dp[i][j] = dp[i][j-1] + nums[n-j] * multipliers[k-1]
   取两者中的较大值作为当前状态

边界条件

• dp[0][0] = 0（初始分数为 0）
• 当 i=0 时只能从末尾取
• 当 j=0 时只能从开头取

3、代码实现

C++

class Solution {public: int maximumScore(vector& nums, vector& multipliers) { int n = nums.size(); // nums数组长度 int m = multipliers.size(); // multipliers数组长度 // 初始化 DP 数组, dp[i][j] 表示从开头取 i 个, 末尾取 j 个时的最大分数 // 初始设为最小整数, 表示这些状态尚未计算或不可达 vector<vector> dp(m + 1, vector(m + 1, INT_MIN)); // 初始状态: 没取任何元素时分数为 0 dp[0][0] = 0; // k 表示当前进行的操作步数 (1 到 m) for (int k = 1; k <= m; ++k) { // i 表示从开头取的元素数 (0 到 k) for (int i = 0; i  0) if (i == 0) {  // 只能从末尾取, nums[n-j] 是当前末尾第 j 个元素  dp[i][j] = dp[i][j - 1] + nums[n - j] * multipliers[k - 1]; } // 情况2: 本次从开头取元素 (i > 0) else if (j == 0) {  // 只能从开头取, nums[i-1] 是当前开头第 i 个元素  dp[i][j] = dp[i - 1][j] + nums[i - 1] * multipliers[k - 1]; } // 情况3: 可以从开头或末尾取, 选择得分更高的方式 else {  dp[i][j] = max(dp[i - 1][j] + nums[i - 1] * multipliers[k - 1], // 从开头取 dp[i][j - 1] + nums[n - j] * multipliers[k - 1] // 从末尾取 ); } } } // 在所有完成 m 次操作的方案中找到最大分数 int res = INT_MIN; for (int i = 0; i <= m; ++i) { res = max(res, dp[i][m - i]); } return res; }};

Java

class Solution { public int maximumScore(int[] nums, int[] multipliers) { int n = nums.length; // nums 数组长度 int m = multipliers.length; // multipliers 数组长度 // 初始化 DP 数组, dp[i][j] 表示从开头取 i 个, 末尾取 j 个时的最大分数 int[][] dp = new int[m + 1][m + 1]; // 初始化为最小整数值, 表示这些状态尚未计算或不可达 for (int i = 0; i <= m; i++) { for (int j = 0; j <= m; j++) { dp[i][j] = Integer.MIN_VALUE; } } // 初始状态: 没取任何元素时分数为0 dp[0][0] = 0; // k 表示当前进行的操作步数 (1 到 m) for (int k = 1; k <= m; k++) { // i 表示从开头取的元素数 (0 到 k) for (int i = 0; i <= k; i++) { int j = k - i; // 从末尾取的元素数 // 情况 1: 本次从末尾取元素 (j > 0) if (i == 0) {  // 只能从末尾取, nums[n-j] 是当前末尾第 j 个元素  dp[i][j] = dp[i][j - 1] + nums[n - j] * multipliers[k - 1]; } // 情况 2: 本次从开头取元素 (i > 0) else if (j == 0) {  // 只能从开头取, nums[i-1] 是当前开头第 i 个元素  dp[i][j] = dp[i - 1][j] + nums[i - 1] * multipliers[k - 1]; } // 情况 3: 可以从开头或末尾取, 选择得分更高的方式 else {  dp[i][j] = Math.max( dp[i - 1][j] + nums[i - 1] * multipliers[k - 1], // 从开头取 dp[i][j - 1] + nums[n - j] * multipliers[k - 1] // 从末尾取  ); } } } // 在所有完成 m 次操作的方案中找最大分数 int res = Integer.MIN_VALUE; for (int i = 0; i <= m; i++) { res = Math.max(res, dp[i][m - i]); // i + (m-i) = m } return res; }}

Python

class Solution: def maximumScore(self, nums: List[int], multipliers: List[int]) -> int: n = len(nums) # nums数组长度 m = len(multipliers) # multipliers数组长度 # 初始化DP数组，dp[i][j]表示从开头取i个，末尾取j个时的最大分数 # 初始设为负无穷，表示这些状态尚未计算或不可达 dp = [[-float(\'inf\')] * (m + 1) for _ in range(m + 1)] # 初始状态：没取任何元素时分数为0 dp[0][0] = 0 # k表示当前进行的操作步数（1到m） for k in range(1, m + 1): # i表示从开头取的元素数（0到k） for i in range(0, k + 1): j = k - i # 从末尾取的元素数 # 情况1：本次从末尾取元素（j > 0） if i == 0:  # 只能从末尾取，nums[n-j]是当前末尾第j个元素  dp[i][j] = dp[i][j-1] + nums[n-j] * multipliers[k-1] # 情况2：本次从开头取元素（i > 0） elif j == 0:  # 只能从开头取，nums[i-1]是当前开头第i个元素  dp[i][j] = dp[i-1][j] + nums[i-1] * multipliers[k-1] # 情况3：可以从开头或末尾取，选择得分更高的方式 else:  dp[i][j] = max( dp[i-1][j] + nums[i-1] * multipliers[k-1], # 从开头取 dp[i][j-1] + nums[n-j] * multipliers[k-1] # 从末尾取  ) # 在所有完成m次操作的方案中找最大分数 return max(dp[i][m-i] for i in range(m + 1))

4、复杂度分析

• 时间复杂度：O(m²)，因为我们填充一个大小为(m+1)×(m+1)的DP表
• 空间复杂度：O(m²)，用于存储DP表

Q9、摘樱桃 II

1、题目描述

给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。

你有两个机器人帮你收集樱桃，机器人 1 从左上角格子 (0,0) 出发，机器人 2 从右上角格子 (0, cols-1) 出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

• 从格子 (i,j) 出发，机器人可以移动到格子 (i+1, j-1)，(i+1, j) 或者 (i+1, j+1) 。
• 当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，然后这个位置会变成空格子，即没有樱桃的格子。
• 当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
• 两个机器人在任意时刻都不能移动到 grid 外面。
• 两个机器人最后都要到达 grid 最底下一行。

示例 1：

输入：grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]输出：24解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。樱桃总数为： 12 + 12 = 24 。

示例 2：

输入：grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]输出：28解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。樱桃总数为： 17 + 11 = 28 。

示例 3：

输入：grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]输出：22

示例 4：

输入：grid = [[1,1],[1,1]]输出：4

提示：

• rows == grid.length
• cols == grid[i].length
• 2 <= rows, cols <= 70
• 0 <= grid[i][j] <= 100

2、解题思路

状态定义

使用 f[j1][j2] 表示：当机器人 1 在第 i 行的 j1 列，机器人 2 在第 i 行的 j2 列时，能收集到的最大樱桃数。

关键思路

1. 两个机器人必须同步向下移动（因为每次只能向下移动一行）
2. 我们需要考虑所有可能的机器人位置组合
3. 当两个机器人位于同一格子时，樱桃只能被收集一次

3、代码实现

C++

class Solution {public: int cherryPickup(vector<vector>& grid) { int m = grid.size(); // 网格行数 int n = grid[0].size(); // 网格列数 // f[j1][j2] 表示当前行两个机器人分别在 j1 和 j2 列时的最大樱桃数 vector<vector> f(n, vector(n, -1)); // 初始化为 -1 表示不可达 vector<vector> g(n, vector(n, -1)); // 临时数组 // 初始状态: 第一行, 机器人 1 在 (0, 0), 机器人 2 在 (0, n-1) f[0][n - 1] = grid[0][0] + grid[0][n - 1]; // 从第二行开始逐行处理 for (int i = 1; i < m; ++i) { // 遍历所有可能的机器人 1 和机器人 2 的位置组合 for (int j1 = 0; j1 < n; ++j1) { for (int j2 = 0; j2 < n; ++j2) {  int best = -1; // 当前组合的最大樱桃树  // 检查上一行所有可能的来源位置 (每个机器人可以从三个方向来)  for (int dj1 = j1 - 1; dj1 <= j1 + 1; ++dj1) // 机器人 1 的来源列  { for (int dj2 = j2 - 1; dj2 = 0 && dj1 = 0 && dj2 < n && f[dj1][dj2] != -1) { // 计算当前樱桃数 int current = f[dj1][dj2]; if (j1 == j2) {  current += grid[i][j1]; // 同一个位置只能加一次 } else {  current += grid[i][j1] + grid[i][j2]; // 不同位置加两次 } best = max(best, current); // 更新最大值 } }  }  g[j1][j2] = best; // 保存当前组合的最大值 } } swap(f, g); // 交换数组, 准备处理下一行 } // 在最后一行找出最大樱桃数 int ans = 0; for (int j1 = 0; j1 < n; ++j1) { for (int j2 = 0; j2 < n; ++j2) { ans = max(ans, f[j1][j2]); } } return ans; }};

Java

class Solution { public int cherryPickup(int[][] grid) { int m = grid.length; // 网格行数 int n = grid[0].length; // 网格列数 // f[j1][j2]表示当前行两个机器人分别在j1和j2列时的最大樱桃数 int[][] f = new int[n][n]; int[][] g = new int[n][n]; // 临时数组 // 初始化为-1表示不可达 for (int j1 = 0; j1 < n; j1++) { Arrays.fill(f[j1], -1); Arrays.fill(g[j1], -1); } // 初始状态：第一行，机器人1在(0,0)，机器人2在(0,n-1) f[0][n - 1] = grid[0][0] + grid[0][n - 1]; // 从第二行开始逐行处理 for (int i = 1; i < m; i++) { // 遍历所有可能的机器人1和机器人2的位置组合 for (int j1 = 0; j1 < n; j1++) { for (int j2 = 0; j2 < n; j2++) {  int best = -1; // 当前组合的最大樱桃数  // 检查上一行所有可能的来源位置  for (int dj1 = j1 - 1; dj1 <= j1 + 1; dj1++) { // 机器人1的来源列 for (int dj2 = j2 - 1; dj2 <= j2 + 1; dj2++) { // 机器人2的来源列 // 检查来源位置是否有效 if (dj1 >= 0 && dj1 < n && dj2 >= 0 && dj2 < n && f[dj1][dj2] != -1) { // 计算当前樱桃数 int current = f[dj1][dj2]; if (j1 == j2) {  current += grid[i][j1]; // 同一位置只能加一次 } else {  current += grid[i][j1] + grid[i][j2]; // 不同位置加两次 } best = Math.max(best, current); // 更新最大值 } }  }  g[j1][j2] = best; // 保存当前组合的最大值 } } // 交换数组，准备处理下一行 int[][] temp = f; f = g; g = temp; } // 在最后一行找出最大的樱桃数 int ans = 0; for (int j1 = 0; j1 < n; j1++) { for (int j2 = 0; j2 < n; j2++) { ans = Math.max(ans, f[j1][j2]); } } return ans; }}

Python

class Solution: def cherryPickup(self, grid: List[List[int]]) -> int: m = len(grid) # 网格行数 n = len(grid[0]) # 网格列数 # f[j1][j2]表示当前行两个机器人分别在j1和j2列时的最大樱桃数 f = [[-1] * n for _ in range(n)] # 初始化为-1表示不可达 g = [[-1] * n for _ in range(n)] # 临时数组 # 初始状态：第一行，机器人1在(0,0)，机器人2在(0,n-1) f[0][n-1] = grid[0][0] + grid[0][n-1] # 从第二行开始逐行处理 for i in range(1, m): # 遍历所有可能的机器人1和机器人2的位置组合 for j1 in range(n): for j2 in range(n):  best = -1 # 当前组合的最大樱桃数  # 检查上一行所有可能的来源位置  for dj1 in [j1-1, j1, j1+1]: # 机器人1的来源列 for dj2 in [j2-1, j2, j2+1]: # 机器人2的来源列 # 检查来源位置是否有效 if 0 <= dj1 < n and 0 <= dj2 < n and f[dj1][dj2] != -1: # 计算当前樱桃数 current = f[dj1][dj2] if j1 == j2:  current += grid[i][j1] # 同一位置只能加一次 else:  current += grid[i][j1] + grid[i][j2] # 不同位置加两次 best = max(best, current) # 更新最大值  g[j1][j2] = best # 保存当前组合的最大值 f, g = g, f # 交换数组，准备处理下一行 # 在最后一行找出最大的樱桃数 ans = 0 for j1 in range(n): for j2 in range(n): ans = max(ans, f[j1][j2]) return ans

4、复杂度分析

• 时间复杂度控制在 O(m*n²)（m行n列）

• 空间复杂度控制在 O(mn²) 或 O(mn²)

Q10、粉刷房子 III

1、题目描述

在一个小城市里，有 m 个房子排成一排，你需要给每个房子涂上 n 种颜色之一（颜色编号为 1 到 n ）。有的房子去年夏天已经涂过颜色了，所以这些房子不可以被重新涂色。

我们将连续相同颜色尽可能多的房子称为一个街区。（比方说 houses = [1,2,2,3,3,2,1,1] ，它包含 5 个街区 [{1}, {2,2}, {3,3}, {2}, {1,1}] 。）

给你一个数组 houses ，一个 m * n 的矩阵 cost 和一个整数 target ，其中：

• houses[i]：是第 i 个房子的颜色，0 表示这个房子还没有被涂色。
• cost[i][j]：是将第 i 个房子涂成颜色 j+1 的花费。

请你返回房子涂色方案的最小总花费，使得每个房子都被涂色后，恰好组成 target 个街区。如果没有可用的涂色方案，请返回 -1 。

示例 1：

输入：houses = [0,0,0,0,0], cost = [[1,10],[10,1],[10,1],[1,10],[5,1]], m = 5, n = 2, target = 3输出：9解释：房子涂色方案为 [1,2,2,1,1]此方案包含 target = 3 个街区，分别是 [{1}, {2,2}, {1,1}]。涂色的总花费为 (1 + 1 + 1 + 1 + 5) = 9。

示例 2：

输入：houses = [0,2,1,2,0], cost = [[1,10],[10,1],[10,1],[1,10],[5,1]], m = 5, n = 2, target = 3输出：11解释：有的房子已经被涂色了，在此基础上涂色方案为 [2,2,1,2,2]此方案包含 target = 3 个街区，分别是 [{2,2}, {1}, {2,2}]。给第一个和最后一个房子涂色的花费为 (10 + 1) = 11。

示例 3：

输入：houses = [0,0,0,0,0], cost = [[1,10],[10,1],[1,10],[10,1],[1,10]], m = 5, n = 2, target = 5输出：5

示例 4：

输入：houses = [3,1,2,3], cost = [[1,1,1],[1,1,1],[1,1,1],[1,1,1]], m = 4, n = 3, target = 3输出：-1解释：房子已经被涂色并组成了 4 个街区，分别是 [{3},{1},{2},{3}] ，无法形成 target = 3 个街区。

提示：

• m == houses.length == cost.length
• n == cost[i].length
• 1 <= m <= 100
• 1 <= n <= 20
• 1 <= target <= m
• 0 <= houses[i] <= n
• 1 <= cost[i][j] <= 10^4

2、解题思路

状态定义

使用三维DP数组dp[i][j][k]表示：

• 前i个房子
• 第i个房子涂颜色j
• 形成k个街区
  的最小花费

关键点

1. 已涂色房子处理：如果房子已涂色，只能选择该颜色
2. 街区计数 ：
   • 颜色与前一个相同：街区数不变
   • 颜色不同：街区数+1
3. 初始状态：第一个房子的处理
4. 结果提取：在最后一个房子所有颜色中找满足target街区的最小花费

3、代码实现

C++

class Solution {private: static constexpr int INF = INT_MAX / 2; // 防止整数溢出public: int minCost(vector& houses, vector<vector>& cost, int m, int n, int target) { // 调整颜色编号: 0 到 n-1, 未涂色设为 -1 for (int& c : houses) { if (c > 0) { c--; } else { c = -1; } } // dp[i][j][k]: 前 i 个房子, 第 i 个涂成 j 颜色, 形成 k 个街区的最小花费 vector<vector<vector>> dp(m, vector<vector>(n, vector(target, INF))); // best[i][k]: 记录前 i 个房子形成 k 个街区时的最小和次小花费及其颜色 vector<vector<tuple>> best(m, vector<tuple>(target, {INF, -1, INF})); for (int i = 0; i < m; ++i) // 对于每个房子 { for (int j = 0; j < n; ++j) // 每种颜色 { // 如果房子已涂色且不是当前颜色, 跳过 if (houses[i] != -1 && houses[i] != j) {  continue; } for (int k = 0; k  0) { auto [first, first_idx, second] = best[i - 1][k - 1]; // 取不同颜色中的最小值 (避免与自己颜色相同) dp[i][j][k] = min(dp[i][j][k], (j == first_idx ? second : first)); }  }  // 如果当前状态可达且房子需要涂色, 加上涂色费用  if (dp[i][j][k] != INF && houses[i] == -1) { dp[i][j][k] += cost[i][j];  }  // 更新 best 数据  auto& [b_first, b_first_idx, b_second] = best[i][k];  if (dp[i][j][k] < b_first) { b_second = b_first; b_first = dp[i][j][k]; b_first_idx = j;  } else if (dp[i][j][k] < b_second) { b_second = dp[i][j][k];  } } } } // 在最后一个房子所有颜色中找满足 target 街区的最小花费 int ans = INF; for (int j = 0; j < n; ++j) { ans = min(ans, dp[m - 1][j][target - 1]); } return ans == INF ? -1 : ans; }};

Java

class Solution { private static final int INFTY = Integer.MAX_VALUE / 2; // 防止整数溢出 public int minCost(int[] houses, int[][] cost, int m, int n, int target) { // 调整颜色编号：0到n-1，未涂色设为-1 for (int i = 0; i < m; i++) { if (houses[i] > 0) { houses[i]--; } else { houses[i] = -1; } } // dp[i][j][k]：前i个房子，第i个涂j色，形成k个街区的最小花费 int[][][] dp = new int[m][n][target]; // 初始化DP数组为极大值 for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { Arrays.fill(dp[i][j], INFTY); } } // best数组记录每个位置形成k个街区时的最小和次小花费及其颜色 int[][][] best = new int[m][target][3]; for (int i = 0; i < m; i++) { for (int k = 0; k < target; k++) { best[i][k][0] = INFTY; // first best[i][k][1] = -1; // first_idx best[i][k][2] = INFTY; // second } } for (int i = 0; i < m; i++) { // 每个房子 for (int j = 0; j < n; j++) { // 每种颜色 // 如果房子已涂色且不是当前颜色，跳过 if (houses[i] != -1 && houses[i] != j) {  continue; } for (int k = 0; k < target; k++) { // 每个目标街区数  if (i == 0) { // 第一个房子的特殊处理 if (k == 0) { dp[i][j][k] = 0; }  } else { // 情况1：与前一个房子颜色相同，街区数不变 dp[i][j][k] = dp[i - 1][j][k]; // 情况2：与前一个房子颜色不同，街区数+1 if (k > 0) { int first = best[i - 1][k - 1][0]; int first_idx = best[i - 1][k - 1][1]; int second = best[i - 1][k - 1][2]; // 取不同颜色中的最小值（避免与自己颜色相同） dp[i][j][k] = Math.min(dp[i][j][k], (j == first_idx ? second : first)); }  }  // 如果当前状态可达且房子需要涂色，加上涂色费用  if (dp[i][j][k] != INFTY && houses[i] == -1) { dp[i][j][k] += cost[i][j];  }  // 更新best数组  if (dp[i][j][k] < best[i][k][0]) { best[i][k][2] = best[i][k][0]; best[i][k][0] = dp[i][j][k]; best[i][k][1] = j;  } else if (dp[i][j][k] < best[i][k][2]) { best[i][k][2] = dp[i][j][k];  } } } } // 在最后一个房子所有颜色中找满足target街区的最小花费 int result = INFTY; for (int j = 0; j < n; j++) { result = Math.min(result, dp[m - 1][j][target - 1]); } return result == INFTY ? -1 : result; }}

Python

class Solution: def minCost(self, houses: List[int], cost: List[List[int]], m: int, n: int, target: int) -> int: # 调整颜色编号：0到n-1，未涂色设为-1 houses = [c-1 if c > 0 else -1 for c in houses] # 初始化DP数组，dp[i][j][k]表示前i个房子，第i个涂j色，形成k个街区的最小花费 # 使用float(\'inf\')表示不可达状态 dp = [[[float(\'inf\')] * target for _ in range(n)] for _ in range(m)] # best数组记录每个位置形成k个街区时的最小和次小花费及其颜色 best = [[(float(\'inf\'), -1, float(\'inf\')) for _ in range(target)] for _ in range(m)] for i in range(m): # 遍历每个房子 for j in range(n): # 遍历每种颜色 # 如果房子已涂色且不是当前颜色，跳过 if houses[i] != -1 and houses[i] != j:  continue for k in range(target): # 遍历目标街区数  if i == 0: # 第一个房子的特殊处理 if k == 0: # 第一个房子形成1个街区 dp[i][j][k] = 0  else: # 情况1：与前一个房子颜色相同，街区数不变 dp[i][j][k] = dp[i-1][j][k] # 情况2：与前一个房子颜色不同，街区数+1 if k > 0: first, first_idx, second = best[i-1][k-1] # 取不同颜色中的最小值（避免与自己颜色相同） dp[i][j][k] = min(dp[i][j][k], second if j == first_idx else first)  # 如果当前状态可达且房子需要涂色，加上涂色费用  if dp[i][j][k] != float(\'inf\') and houses[i] == -1: dp[i][j][k] += cost[i][j]  # 更新best数组  b_first, b_first_idx, b_second = best[i][k]  if dp[i][j][k] < b_first: b_second = b_first b_first = dp[i][j][k] b_first_idx = j  elif dp[i][j][k] < b_second: b_second = dp[i][j][k]  best[i][k] = (b_first, b_first_idx, b_second) # 在最后一个房子所有颜色中找满足target街区的最小花费 result = min(dp[m-1][j][target-1] for j in range(n)) return result if result != float(\'inf\') else -1

4、复杂度分析

• 时间复杂度：O(m n target)
  • 三重循环：房子数(m) × 颜色数(n) × 目标街区数(target)
• 空间复杂度：O(m n target)
  • 三维DP数组存储状态

Q11、青蛙过河

1、题目描述

一只青蛙想要过河。 假定河流被等分为若干个单元格，并且在每一个单元格内都有可能放有一块石子（也有可能没有）。 青蛙可以跳上石子，但是不可以跳入水中。

给你石子的位置列表 stones（用单元格序号 升序 表示）， 请判定青蛙能否成功过河（即能否在最后一步跳至最后一块石子上）。开始时， 青蛙默认已站在第一块石子上，并可以假定它第一步只能跳跃 1 个单位（即只能从单元格 1 跳至单元格 2 ）。

如果青蛙上一步跳跃了 k 个单位，那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意，青蛙只能向前方（终点的方向）跳跃。

示例 1：

输入：stones = [0,1,3,5,6,8,12,17]输出：true解释：青蛙可以成功过河，按照如下方案跳跃：跳 1 个单位到第 2 块石子, 然后跳 2 个单位到第 3 块石子, 接着 跳 2 个单位到第 4 块石子, 然后跳 3 个单位到第 6 块石子, 跳 4 个单位到第 7 块石子, 最后，跳 5 个单位到第 8 个石子（即最后一块石子）。

示例 2：

输入：stones = [0,1,2,3,4,8,9,11]输出：false解释：这是因为第 5 和第 6 个石子之间的间距太大，没有可选的方案供青蛙跳跃过去。

提示：

• 2 <= stones.length <= 2000
• 0 <= stones[i] <= 231 - 1
• stones[0] == 0
• stones 按严格升序排列

2、解题思路

方法一：记忆化DFS（递归+记忆化）

1. 使用深度优先搜索尝试所有可能的跳跃路径
2. 对于每个位置和跳跃距离，记录是否能到达终点
3. 使用记忆化技术避免重复计算相同状态
4. 通过二分查找快速定位下一个石头位置

方法二：动态规划（迭代）

1. 使用哈希表记录每个石头位置可以到达的跳跃距离
2. 从第一个石头开始，逐步计算每个石头可达的跳跃距离
3. 对于每个可能的跳跃距离，计算下一跳可能到达的石头
4. 最后检查终点是否有可达的跳跃距离

3、代码实现

C++

// 方法1: 记忆化 DFS (递归 + 记忆化)class Solution {private: // 记忆化 DFS 解法 vector<unordered_map> memo; // 记忆化数组 bool dfs(vector& stones, int index, int lastJump) { // 如果已经到达最后一块石头, 返回成功 if (index == stones.size() - 1) { return true; } // 如果已经计算过这个状态, 直接返回结果 if (memo[index].count(lastJump)) { return memo[index][lastJump]; } // 尝试三种可能的跳跃距离 for (int jump = lastJump - 1; jump  0) // 跳跃距离必须大于 0 { // 计算下一个石头的位置 int nextPos = stones[index] + jump; // 使用二分查找确定下一个石头是否存在 auto it = lower_bound(stones.begin() + index + 1, stones.end(), nextPos); if (it != stones.end() && *it == nextPos) {  int nextIndex = it - stones.begin();  // 递归检查是否能到达终点  if (dfs(stones, nextIndex, jump)) { return memo[index][lastJump] = true;  } } } } // 记录当前状态结果 return memo[index][lastJump] = false; }public: bool canCross(vector& stones) { memo.resize(stones.size()); return dfs(stones, 0, 0); }};

// 方法2: 动态规划class Solution {public: bool canCross(vector& stones) { int n = stones.size(); // 使用哈希表存储每个石头位置可达的跳跃距离 unordered_map<int, unordered_set> dp; for (int stone : stones) { dp[stone] = unordered_set(); } // 初始状态: 位置 0, 跳跃距离 0 dp[stones[0]].insert(0); for (int i = 0; i < n; ++i) { int current = stones[i]; for (int k : dp[current]) { // 尝试三种可能的跳跃 for (int step = k - 1; step  0) { int next = current + step; // 如果直接到达终点, 返回成功 if (next == stones.back()) { return true; } // 如果这个位置有石头, 记录跳跃距离 if (dp.count(next)) { dp[next].insert(step); }  } } } } // 检查终点是否有可达的跳跃高度 return !dp[stones.back()].empty(); }};

Java

// 方法1: 记忆化 DFS (递归 + 记忆化)class Solution { // 方法一：记忆化DFS private Map<Integer, Boolean>[] memo; private boolean dfs(int[] stones, int index, int lastJump) { // 到达终点返回true if (index == stones.length - 1) { return true; } // 检查是否已计算过 if (memo[index].containsKey(lastJump)) { return memo[index].get(lastJump); } // 尝试三种跳跃距离 for (int jump = lastJump - 1; jump <= lastJump + 1; jump++) { if (jump > 0) { int nextPos = stones[index] + jump; // 使用二分查找确定下一个石头位置 int nextIndex = Arrays.binarySearch(stones, index + 1, stones.length, nextPos); if (nextIndex >= 0 && dfs(stones, nextIndex, jump)) {  memo[index].put(lastJump, true);  return true; } } } memo[index].put(lastJump, false); return false; } public boolean canCross(int[] stones) { memo = new HashMap[stones.length]; for (int i = 0; i < stones.length; i++) { memo[i] = new HashMap<>(); } return dfs(stones, 0, 0); }}

// 方法2: 动态规划class Solution { public boolean canCross(int[] stones) { int n = stones.length; // 使用哈希表存储每个位置可达的跳跃距离 Map<Integer, Set<Integer>> dp = new HashMap<>(); for (int stone : stones) { dp.put(stone, new HashSet<>()); } // 初始状态：位置0，跳跃距离0 dp.get(stones[0]).add(0); for (int i = 0; i < n; i++) { int current = stones[i]; // 遍历当前石头所有可能的跳跃距离 for (int k : dp.get(current)) { // 尝试三种可能的跳跃 for (int step = k - 1; step <= k + 1; step++) {  if (step > 0) { int next = current + step; // 如果直接到达终点，返回成功 if (next == stones[n - 1]) { return true; } // 如果这个位置有石头，记录跳跃距离 if (dp.containsKey(next)) { dp.get(next).add(step); }  } } } } // 检查终点是否有可达的跳跃距离 return !dp.get(stones[n - 1]).isEmpty(); }}

Python

# 方法1: 记忆化 DFS (递归 + 记忆化)class Solution: def canCross(self, stones: List[int]) -> bool: stone_set = set(stones) last_stone = stones[-1] @lru_cache(maxsize=None) def dfs(position, last_jump): # 到达终点返回True if position == last_stone: return True # 尝试三种可能的跳跃距离 for jump in (last_jump-1, last_jump, last_jump+1): if jump > 0: # 跳跃距离必须大于0  next_pos = position + jump  # 检查下一个石头是否存在  if next_pos in stone_set: if dfs(next_pos, jump): return True return False return dfs(stones[0], 0)

# 方法2: 动态规划class Solution: def canCross(self, stones: List[int]) -> bool: n = len(stones) # 使用字典存储每个位置可达的跳跃距离 dp = {stone: set() for stone in stones} # 初始状态：位置0，跳跃距离0 dp[0].add(0) for i in range(n): current = stones[i] # 遍历当前石头所有可能的跳跃距离 for k in list(dp[current]): # 尝试三种可能的跳跃 for step in (k-1, k, k+1):  if step > 0: next_pos = current + step # 如果直接到达终点，返回成功 if next_pos == stones[-1]: return True # 如果这个位置有石头，记录跳跃距离 if next_pos in dp: dp[next_pos].add(step) # 检查终点是否有可达的跳跃距离 return len(dp[stones[-1]]) > 0

4、复杂度分析

方法一：记忆化DFS（递归+记忆化）

• 时间复杂度：O(n²) - 每个状态最多计算一次，共有n×n个可能状态
• 空间复杂度：O(n²) - 用于存储记忆化结果

方法二：动态规划（迭代）

• 时间复杂度：O(n²) - 每个石头最多被检查n次
• 空间复杂度：O(n²) - 需要存储每个石头可达的跳跃距离

Q12、工作计划的最低难度

1、题目描述

你需要制定一份 d 天的工作计划表。工作之间存在依赖，要想执行第 i 项工作，你必须完成全部 j 项工作（ 0 <= j < i）。

你每天 至少 需要完成一项任务。工作计划的总难度是这 d 天每一天的难度之和，而一天的工作难度是当天应该完成工作的最大难度。

给你一个整数数组 jobDifficulty 和一个整数 d，分别代表工作难度和需要计划的天数。第 i 项工作的难度是 jobDifficulty[i]。

返回整个工作计划的 最小难度 。如果无法制定工作计划，则返回 -1 。

示例 1：

输入：jobDifficulty = [6,5,4,3,2,1], d = 2输出：7解释：第一天，您可以完成前 5 项工作，总难度 = 6.第二天，您可以完成最后一项工作，总难度 = 1.计划表的难度 = 6 + 1 = 7 

示例 2：

输入：jobDifficulty = [9,9,9], d = 4输出：-1解释：就算你每天完成一项工作，仍然有一天是空闲的，你无法制定一份能够满足既定工作时间的计划表。

示例 3：

输入：jobDifficulty = [1,1,1], d = 3输出：3解释：工作计划为每天一项工作，总难度为 3 。

示例 4：

输入：jobDifficulty = [7,1,7,1,7,1], d = 3输出：15

示例 5：

输入：jobDifficulty = [11,111,22,222,33,333,44,444], d = 6输出：843

提示：

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

2、解题思路

方法一：基础动态规划

1. 状态定义：dp[i][j] 表示前j个任务分成 i+1 天完成的最小总难度
2. 初始化：dp[0][j] 表示 1 天内完成前j个任务的最大难度
3. 状态转移：对于第 i 天，考虑从k到j的任务作为一天，取最小总难度

方法二：空间优化动态规划

1. 观察到 dp[i] 只依赖于 dp[i-1]，可以优化空间
2. 使用两个一维数组交替更新，减少空间使用

方法三：单调栈优化动态规划

1. 利用单调栈优化寻找最大值的过程
2. 维护一个递减栈，快速计算区间最大值

方法四：空间优化+单调栈动态规划

1. 结合方法二和方法三的优点
2. 使用单调栈优化最大值计算，同时优化空间使用

3、代码实现

C++

// 方法1: 动态规划class Solution {public: int minDifficulty(vector& jobDifficulty, int d) { int n = jobDifficulty.size(); if (n < d) { return -1; // 任务数不足天数, 无法分配 } // dp[i][j]: 前 j+1 个任务 分成 i+1 天的最小总难度 vector<vector> dp(d, vector(n, INT_MAX)); // 初始化: 1 天完成前 j+1 个任务的最大难度 int max_val = 0; for (int j = 0; j < n; ++j) { max_val = max(max_val, jobDifficulty[j]); dp[0][j] = max_val; } for (int i = 1; i < d; ++i) // 从第二天开始 { for (int j = i; j = i; --k) {  day_max = max(day_max, jobDifficulty[k]);  dp[i][j] = min(dp[i][j], dp[i - 1][k - 1] + day_max); } } } return dp[d - 1][n - 1]; }};

// 方法2: 动态规划空间优化class Solution {public: int minDifficulty(vector& jobDifficulty, int d) { int n = jobDifficulty.size(); if (n < d) { return -1; } vector dp(n); // 初始化: 1 天完成前 j+1 个任务的最大难度 int max_val = 0; for (int j = 0; j < n; ++j) { max_val = max(max_val, jobDifficulty[j]); dp[j] = max_val; } for (int i = 1; i < d; ++i) { vector new_dp(n, INT_MAX); for (int j = i; j = i; --k) {  day_max = max(day_max, jobDifficulty[k]);  new_dp[j] = min(new_dp[j], dp[k - 1] + day_max); } } swap(dp, new_dp); } return dp[n - 1]; }};

// 方法3: 单调栈动态规划class Solution {public: int minDifficulty(vector& jobDifficulty, int d) { int n = jobDifficulty.size(); if (n < d) { return -1; } vector<vector> dp(d, vector(n)); // 初始化第 i 天 for (int j = 0, max_val = 0; j < n; ++j) { max_val = max(max_val, jobDifficulty[j]); dp[0][j] = max_val; } for (int i = 1; i < d; ++i) { stack<pair> st; // {index, min_val} for (int j = i; j < n; ++j) { int min_val = dp[i - 1][j - 1]; // 维护单调递减栈 while (!st.empty() && jobDifficulty[st.top().first] <= jobDifficulty[j]) {  min_val = min(min_val, st.top().second);  st.pop(); } if (st.empty()) {  dp[i][j] = min_val + jobDifficulty[j]; } else {  dp[i][j] = min(dp[i][st.top().first], min_val + jobDifficulty[j]); } st.emplace(j, min_val); } } return dp[d - 1][n - 1]; }};

// 方法4: 单调栈动态规划空间优化class Solution {public: int minDifficulty(vector& jobDifficulty, int d) { int n = jobDifficulty.size(); if (n < d) { return -1; } vector dp(n); // 初始化第 1 天 for (int j = 0, max_val = 0; j < n; ++j) { max_val = max(max_val, jobDifficulty[j]); dp[j] = max_val; } for (int i = 1; i < d; ++i) { vector new_dp(n, INT_MAX); stack<pair> st; // {index, min_val} for (int j = i; j < n; ++j) { int min_val = dp[j - 1]; // 维护单调递减栈 while (!st.empty() && jobDifficulty[st.top().first] <= jobDifficulty[j]) {  min_val = min(min_val, st.top().second);  st.pop(); } if (st.empty()) {  new_dp[j] = min_val + jobDifficulty[j]; } else {  new_dp[j] = min(new_dp[st.top().first], min_val + jobDifficulty[j]); } st.emplace(j, min_val); } swap(dp, new_dp); } return dp[n - 1]; }};

Java

// 方法1: 动态规划class Solution { public int minDifficulty(int[] jobDifficulty, int d) { int n = jobDifficulty.length; if (n < d) { return -1; } int[][] dp = new int[d][n]; for (int[] row : dp) { Arrays.fill(row, Integer.MAX_VALUE); } int max = 0; for (int j = 0; j < n; j++) { max = Math.max(max, jobDifficulty[j]); dp[0][j] = max; } for (int i = 1; i < d; i++) { for (int j = i; j < n; j++) { int dayMax = 0; for (int k = j; k >= i; k--) {  dayMax = Math.max(dayMax, jobDifficulty[k]);  dp[i][j] = Math.min(dp[i][j], dp[i - 1][k - 1] + dayMax); } } } return dp[d - 1][n - 1]; }}

// 方法2: 动态规划空间优化class Solution { public int minDifficulty(int[] jobDifficulty, int d) { int n = jobDifficulty.length; if (n < d) { return -1; } int[] dp = new int[n]; int max = 0; for (int j = 0; j < n; j++) { max = Math.max(max, jobDifficulty[j]); dp[j] = max; } for (int i = 1; i < d; i++) { int[] newDp = new int[n]; Arrays.fill(newDp, Integer.MAX_VALUE); for (int j = i; j < n; j++) { int dayMax = 0; for (int k = j; k >= i; k--) {  dayMax = Math.max(dayMax, jobDifficulty[k]);  newDp[j] = Math.min(newDp[j], dp[k - 1] + dayMax); } } dp = newDp; } return dp[n - 1]; }}

// 方法3: 单调栈动态规划class Solution { public int minDifficulty(int[] jobDifficulty, int d) { int n = jobDifficulty.length; if (n < d) { return -1; } int[][] dp = new int[d][n]; int max = 0; for (int j = 0; j < n; j++) { max = Math.max(max, jobDifficulty[j]); dp[0][j] = max; } for (int i = 1; i < d; i++) { Deque<int[]> stack = new ArrayDeque<>(); for (int j = i; j < n; j++) { int minVal = dp[i - 1][j - 1]; while (!stack.isEmpty() && jobDifficulty[stack.peek()[0]] <= jobDifficulty[j]) {  minVal = Math.min(minVal, stack.pop()[1]); } if (stack.isEmpty()) {  dp[i][j] = minVal + jobDifficulty[j]; } else {  dp[i][j] = Math.min(dp[i][stack.peek()[0]], minVal + jobDifficulty[j]); } stack.push(new int[] { j, minVal }); } } return dp[d - 1][n - 1]; }}

// 方法4: 单调栈动态规划空间优化class Solution { public int minDifficulty(int[] jobDifficulty, int d) { int n = jobDifficulty.length; if (n < d) { return -1; } int[] dp = new int[n]; int max = 0; for (int j = 0; j < n; j++) { max = Math.max(max, jobDifficulty[j]); dp[j] = max; } for (int i = 1; i < d; i++) { int[] newDp = new int[n]; Arrays.fill(newDp, Integer.MAX_VALUE); Deque<int[]> stack = new ArrayDeque<>(); for (int j = i; j < n; j++) { int minVal = dp[j - 1]; while (!stack.isEmpty() && jobDifficulty[stack.peek()[0]] <= jobDifficulty[j]) {  minVal = Math.min(minVal, stack.pop()[1]); } if (stack.isEmpty()) {  newDp[j] = minVal + jobDifficulty[j]; } else {  newDp[j] = Math.min(newDp[stack.peek()[0]], minVal + jobDifficulty[j]); } stack.push(new int[] { j, minVal }); } dp = newDp; } return dp[n - 1]; }}

Python

# 方法1: 动态规划class Solution: def minDifficulty(self, jobDifficulty: List[int], d: int) -> int: n = len(jobDifficulty) if n < d: return -1 dp = [[float(\'inf\')] * n for _ in range(d)] max_val = 0 for j in range(n): max_val = max(max_val, jobDifficulty[j]) dp[0][j] = max_val for i in range(1, d): for j in range(i, n): day_max = 0 for k in range(j, i-1, -1):  day_max = max(day_max, jobDifficulty[k])  dp[i][j] = min(dp[i][j], dp[i-1][k-1] + day_max) return dp[-1][-1] if dp[-1][-1] != float(\'inf\') else -1

# 方法2: 动态规划空间优化class Solution: def minDifficulty(self, jobDifficulty: List[int], d: int) -> int: n = len(jobDifficulty) if n < d: return -1 dp = [0] * n max_val = 0 for j in range(n): max_val = max(max_val, jobDifficulty[j]) dp[j] = max_val for i in range(1, d): new_dp = [float(\'inf\')] * n for j in range(i, n): day_max = 0 for k in range(j, i-1, -1):  day_max = max(day_max, jobDifficulty[k])  new_dp[j] = min(new_dp[j], dp[k-1] + day_max) dp = new_dp return dp[-1] if dp[-1] != float(\'inf\') else -1

# 方法3: 单调栈动态规划class Solution: def minDifficulty(self, jobDifficulty: List[int], d: int) -> int: n = len(jobDifficulty) if n < d: return -1 dp = [[0] * n for _ in range(d)] max_val = 0 for j in range(n): max_val = max(max_val, jobDifficulty[j]) dp[0][j] = max_val for i in range(1, d): stack = [] for j in range(i, n): min_val = dp[i-1][j-1] while stack and jobDifficulty[stack[-1][0]] <= jobDifficulty[j]:  min_val = min(min_val, stack.pop()[1]) if not stack:  dp[i][j] = min_val + jobDifficulty[j] else:  dp[i][j] = min(dp[i][stack[-1][0]], min_val + jobDifficulty[j]) stack.append((j, min_val)) return dp[-1][-1] if dp[-1][-1] != float(\'inf\') else -1

# 方法4: 单调栈动态规划空间优化class Solution: def minDifficulty(self, jobDifficulty: List[int], d: int) -> int: n = len(jobDifficulty) if n < d: return -1 dp = [0] * n max_val = 0 for j in range(n): max_val = max(max_val, jobDifficulty[j]) dp[j] = max_val for i in range(1, d): new_dp = [float(\'inf\')] * n stack = [] for j in range(i, n): min_val = dp[j-1] while stack and jobDifficulty[stack[-1][0]] <= jobDifficulty[j]:  min_val = min(min_val, stack.pop()[1]) if not stack:  new_dp[j] = min_val + jobDifficulty[j] else:  new_dp[j] = min(new_dp[stack[-1][0]], min_val + jobDifficulty[j]) stack.append((j, min_val)) dp = new_dp return dp[-1] if dp[-1] != float(\'inf\') else -1

4、复杂度分析

方法一：基础动态规划

• 时间复杂度：O(d·n²)
• 空间复杂度：O(d·n)

方法二：空间优化动态规划

• 时间复杂度：O(d·n²)
• 空间复杂度：O(n)

方法三：单调栈优化动态规划

• 时间复杂度：O(d·n)
• 空间复杂度：O(d·n)

方法四：空间优化+单调栈动态规划

• 时间复杂度：O(d·n)
• 空间复杂度：O(n)

Q13、奇怪的打印机

1、题目描述

有台奇怪的打印机有以下两个特殊要求：

• 打印机每次只能打印由 同一个字符 组成的序列。
• 每次可以在从起始到结束的任意位置打印新字符，并且会覆盖掉原来已有的字符。

给你一个字符串 s ，你的任务是计算这个打印机打印它需要的最少打印次数。

示例 1：

输入：s = \"aaabbb\"输出：2解释：首先打印 \"aaa\" 然后打印 \"bbb\"。

示例 2：

输入：s = \"aba\"输出：2解释：首先打印 \"aaa\" 然后在第二个位置打印 \"b\" 覆盖掉原来的字符 \'a\'。

提示：

• 1 <= s.length <= 100
• s 由小写英文字母组成

2、解题思路

这是一个典型的动态规划问题。我们可以定义 f[i][j] 表示打印字符串 s[i..j] 所需的最少打印次数。我们需要考虑以下几种情况：

1. 基础情况：当 i == j 时，只需要一次打印。
2. 字符相同：如果 s[i] == s[j]，则打印 s[i..j] 可以和打印 s[i..j-1] 的次数相同，因为可以在打印 s[i..j-1] 的最后一步覆盖到 j。
3. 字符不同：如果 s[i] != s[j]，则需要将字符串分成两部分，分别打印，再将结果相加。

方法一：动态规划

• 初始化二维数组 f，其中 f[i][j] 表示打印 s[i..j] 的最少次数。
• 填充 f 数组，从短到长的子串依次计算。

3、代码实现

C++

class Solution {public: int strangePrinter(string s) { int n = s.length(); vector<vector> f(n, vector(n, 0)); // f[i][j] 表示打印 s[i..j] 的最小次数 for (int i = n - 1; i >= 0; --i) // 从后往前遍历 { f[i][i] = 1;  // 单个字符只需要打印一次 for (int j = i + 1; j < n; ++j) // 从 i 到 j 的子串 { if (s[i] == s[j]) // 如果两端字符相同 {  f[i][j] = f[i][j - 1]; // 相当于在打印 s[i..j-1] 的最后一步覆盖到 j } else// 两端字符不同 {  int minn = INT_MAX;  for (int k = i; k < j; ++k) // 尝试所有的分割点  { minn = min(minn, f[i][k] + f[k + 1][j]); // 分割成两部分分别打印  }  f[i][j] = minn; } } } return f[0][n - 1]; // 返回整个字符串的最少打印次数 }};

Java

class Solution { public int strangePrinter(String s) { int n = s.length(); int[][] f = new int[n][n]; // f[i][j] 表示打印 s[i..j] 的最少次数 for (int i = n - 1; i >= 0; --i) { // 从后往前遍历 f[i][i] = 1; // 单个字符只需要打印一次 for (int j = i + 1; j < n; ++j) { // 从 i 到 j 的子串 if (s.charAt(i) == s.charAt(j)) { // 如果两端字符相同  f[i][j] = f[i][j - 1]; // 相当于在打印 s[i..j-1] 的最后一步覆盖到 j } else { // 两端字符不同  int minn = Integer.MAX_VALUE;  for (int k = i; k < j; ++k) { // 尝试所有分割点 minn = Math.min(minn, f[i][k] + f[k + 1][j]); // 分割成两部分分别打印  }  f[i][j] = minn; } } } return f[0][n - 1]; // 返回整个字符串的最少打印次数 }}

Python

class Solution: def strangePrinter(self, s: str) -> int: n = len(s) f = [[0] * n for _ in range(n)] # f[i][j] 表示打印 s[i..j] 的最少次数 for i in range(n - 1, -1, -1): # 从后往前遍历 f[i][i] = 1 # 单个字符只需要打印一次 for j in range(i + 1, n): # 从 i 到 j 的子串 if s[i] == s[j]: # 如果两端字符相同  f[i][j] = f[i][j - 1] # 相当于在打印 s[i..j-1] 的最后一步覆盖到 j else: # 两端字符不同  minn = float(\'inf\')  for k in range(i, j): # 尝试所有分割点 minn = min(minn, f[i][k] + f[k + 1][j]) # 分割成两部分分别打印  f[i][j] = minn return f[0][n - 1] # 返回整个字符串的最少打印次数

4、复杂度分析

方法一：动态规划

• 时间复杂度：O(n³)，其中 n 是字符串的长度。我们需要三重循环来填充 f 数组。
• 空间复杂度：O(n²)，用于存储 f 数组。

Q14、切棍子的最小成本

1、题目描述

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

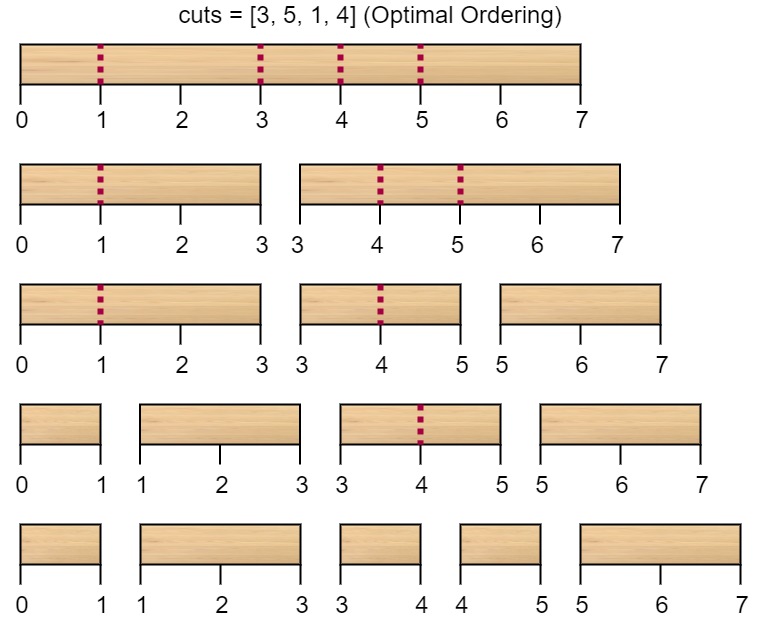
输入：n = 7, cuts = [1,3,4,5]输出：16解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2]输出：22解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：

• 2 <= n <= 10^6
• 1 <= cuts.length <= min(n - 1, 100)
• 1 <= cuts[i] <= n - 1
• cuts 数组中的所有整数都 互不相同

2、解题思路

这是一个典型的动态规划问题，类似于矩阵链乘法问题。我们可以定义 f[i][j] 表示切割从第 i 个切割点到第 j 个切割点之间的木棍所需的最小成本。为了处理边界情况，我们可以在 cuts 数组的开头和结尾分别添加 0 和 n，表示木棍的起点和终点。

1. 排序切割点：首先将 cuts 排序，并在开头和结尾添加 0 和 n。
2. 动态规划填充：使用二维数组 f 来存储子问题的解，f[i][j] 表示切割 cuts[i..j] 的最小成本。
3. 状态转移：对于每个子区间 [i, j]，尝试所有可能的切割点 k，将区间分成两部分，计算两部分的最小成本之和，加上当前区间的长度（即当前切割的成本）。

方法一：动态规划

• 初始化二维数组 f，其中 f[i][j] 表示切割 cuts[i..j] 的最小成本。
• 填充 f 数组，从短到长的子区间依次计算。
• 对于每个子区间 [i, j]，尝试所有可能的切割点 k，计算 f[i][k-1] + f[k+1][j] + (cuts[j+1] - cuts[i-1])，并取最小值。

方法二：记忆化搜索

• 使用递归加记忆化的方式，避免重复计算子问题。
• 定义 dp(i, j) 表示切割 cuts[i..j] 的最小成本，使用哈希表或数组存储已计算的子问题结果。

3、代码实现

C++

// 方法1: 动态规划class Solution {public: int minCost(int n, vector& cuts) { int m = cuts.size(); sort(cuts.begin(), cuts.end()); // 排序切割点 cuts.insert(cuts.begin(), 0); // 添加起始点 cuts.push_back(n);  // 添加终点 vector<vector> f(m + 2, vector(m + 2, 0)); // f[i][j] 表示切割 cuts[i..j] 的最小成本 for (int i = m; i >= 1; --i) // 从后往前遍历 { for (int j = i; j <= m; ++j) // 从左往右遍历 { if (i == j) // 只有一个切割点 {  f[i][j] = cuts[j + 1] - cuts[i - 1]; // 当前区间的长度 } else {  f[i][j] = INT_MAX;  // 初始化为最大值  for (int k = i; k <= j; ++k) // 尝试所有可能的切割点  { f[i][j] = min(f[i][j], f[i][k - 1] + f[k + 1][j]);  }  f[i][j] += cuts[j + 1] - cuts[i - 1]; // 加上当前区间的长度 } } } return f[1][m]; // 返回整个切割的最小成本 }};

// 方法2: 记忆化搜索class Solution {public: int minCost(int n, vector& cuts) { int m = cuts.size(); sort(cuts.begin(), cuts.end()); cuts.insert(cuts.begin(), 0); cuts.push_back(n); vector<vector> memo(m + 2, vector(m + 2, -1)); // 记忆化数组 function dp = [&](int i, int j) { if (i > j) { return 0; } if (memo[i][j] != -1) { return memo[i][j]; } if (i == j) { memo[i][j] = cuts[j + 1] - cuts[i - 1]; return memo[i][j]; } int res = INT_MAX; for (int k = i; k <= j; ++k) { res = min(res, dp(i, k - 1) + dp(k + 1, j)); } res += cuts[j + 1] - cuts[i - 1]; memo[i][j] = res; return res; }; return dp(1, m); }};

Java

// 方法1: 动态规划class Solution { public int minCost(int n, int[] cuts) { int m = cuts.length; Arrays.sort(cuts); // 排序切割点 int[] newCuts = new int[m + 2]; newCuts[0] = 0; // 添加起始点 System.arraycopy(cuts, 0, newCuts, 1, m); newCuts[m + 1] = n; // 添加终点 int[][] f = new int[m + 2][m + 2]; // f[i][j] 表示切割 newCuts[i..j] 的最小成本 for (int i = m; i >= 1; --i) { // 从后往前遍历 for (int j = i; j <= m; ++j) { // 从左到右遍历 if (i == j) { // 只有一个切割点  f[i][j] = newCuts[j + 1] - newCuts[i - 1]; // 当前区间的长度 } else {  f[i][j] = Integer.MAX_VALUE; // 初始化为最大值  for (int k = i; k <= j; ++k) { // 尝试所有可能的切割点 f[i][j] = Math.min(f[i][j], f[i][k - 1] + f[k + 1][j]);  }  f[i][j] += newCuts[j + 1] - newCuts[i - 1]; // 加上当前区间的长度 } } } return f[1][m]; // 返回整个切割的最小成本 }}

// 方法2: 记忆化搜索class Solution { private int[][] memo; public int minCost(int n, int[] cuts) { int m = cuts.length; Arrays.sort(cuts); int[] newCuts = new int[m + 2]; newCuts[0] = 0; System.arraycopy(cuts, 0, newCuts, 1, m); newCuts[m + 1] = n; memo = new int[m + 2][m + 2]; for (int[] row : memo) { Arrays.fill(row, -1); } return dp(1, m, newCuts); } private int dp(int i, int j, int[] cuts) { if (i > j) { return 0; } if (memo[i][j] != -1) { return memo[i][j]; } if (i == j) { memo[i][j] = cuts[j + 1] - cuts[i - 1]; return memo[i][j]; } int res = Integer.MAX_VALUE; for (int k = i; k <= j; ++k) { res = Math.min(res, dp(i, k - 1, cuts) + dp(k + 1, j, cuts)); } res += cuts[j + 1] - cuts[i - 1]; memo[i][j] = res; return res; }}

Python

# 方法1: 动态规划class Solution: def minCost(self, n: int, cuts: List[int]) -> int: m = len(cuts) cuts.sort() # 排序切割点 cuts = [0] + cuts + [n] # 添加起始点和终点 f = [[0] * (m + 2) for _ in range(m + 2)] # f[i][j] 表示切割 cuts[i..j] 的最小成本 for i in range(m, 0, -1): # 从后往前遍历 for j in range(i, m + 1): # 从左到右遍历 if i == j: # 只有一个切割点  f[i][j] = cuts[j + 1] - cuts[i - 1] # 当前区间的长度 else:  f[i][j] = float(\'inf\') # 初始化为最大值  for k in range(i, j + 1): # 尝试所有可能的切割点 f[i][j] = min(f[i][j], f[i][k - 1] + f[k + 1][j])  f[i][j] += cuts[j + 1] - cuts[i - 1] # 加上当前区间的长度 return f[1][m] # 返回整个切割的最小成本

# 方法2: 记忆化搜索class Solution: def minCost(self, n: int, cuts: List[int]) -> int: m = len(cuts) cuts.sort() cuts = [0] + cuts + [n] memo = [[-1] * (m + 2) for _ in range(m + 2)] def dp(i, j): if i > j: return 0 if memo[i][j] != -1: return memo[i][j] if i == j: memo[i][j] = cuts[j + 1] - cuts[i - 1] return memo[i][j] res = float(\'inf\') for k in range(i, j + 1): res = min(res, dp(i, k - 1) + dp(k + 1, j)) res += cuts[j + 1] - cuts[i - 1] memo[i][j] = res return res return dp(1, m)

4、复杂度分析

方法一：动态规划

• 时间复杂度：O(m³)，其中 m 是 cuts 的长度。因为有三重循环。
• 空间复杂度：O(m²)，用于存储 f 数组。

方法二：记忆化搜索

• 时间复杂度：O(m³)，与动态规划相同，但实际运行时间可能因递归开销而略高。
• 空间复杂度：O(m²)，用于存储子问题的解。

Q15、统计所有可行路径

1、题目描述

给你一个 互不相同 的整数数组，其中 locations[i] 表示第 i 个城市的位置。同时给你 start，finish 和 fuel 分别表示出发城市、目的地城市和你初始拥有的汽油总量

每一步中，如果你在城市 i ，你可以选择任意一个城市 j ，满足 j != i 且 0 <= j < locations.length ，并移动到城市 j 。从城市 i 移动到 j 消耗的汽油量为 |locations[i] - locations[j]|，|x| 表示 x 的绝对值。

请注意， fuel 任何时刻都 不能 为负，且你 可以 经过任意城市超过一次（包括 start 和 finish ）。

请你返回从 start 到 finish 所有可能路径的数目。

由于答案可能很大， 请将它对 10^9 + 7 取余后返回。

示例 1：

输入：locations = [2,3,6,8,4], start = 1, finish = 3, fuel = 5输出：4解释：以下为所有可能路径，每一条都用了 5 单位的汽油：1 -> 31 -> 2 -> 31 -> 4 -> 31 -> 4 -> 2 -> 3

示例 2：

输入：locations = [4,3,1], start = 1, finish = 0, fuel = 6输出：5解释：以下为所有可能的路径：1 -> 0，使用汽油量为 fuel = 11 -> 2 -> 0，使用汽油量为 fuel = 51 -> 2 -> 1 -> 0，使用汽油量为 fuel = 51 -> 0 -> 1 -> 0，使用汽油量为 fuel = 31 -> 0 -> 1 -> 0 -> 1 -> 0，使用汽油量为 fuel = 5

示例 3：

输入：locations = [5,2,1], start = 0, finish = 2, fuel = 3输出：0解释：没有办法只用 3 单位的汽油从 0 到达 2 。因为最短路径需要 4 单位的汽油。

提示：

• 2 <= locations.length <= 100
• 1 <= locations[i] <= 109
• 所有 locations 中的整数 互不相同 。
• 0 <= start, finish < locations.length
• 1 <= fuel <= 200

2、解题思路

这是一个典型的动态规划问题。我们可以定义 dp[pos][rest] 表示在当前城市 pos 且剩余汽油量为 rest 时，能够到达 finish 的路径数目。通过递归或迭代的方式填充 dp 数组，最终得到 dp[start][fuel] 的值。

方法一：记忆化搜索（DFS + Memoization）

• 使用深度优先搜索（DFS）遍历所有可能的路径。
• 使用记忆化技术（Memoization）存储已经计算过的子问题结果，避免重复计算。
• 对于每个城市 pos 和剩余汽油量 rest，尝试所有可能的移动方向，递归计算路径数目。

方法二：动态规划（DP）

• 使用动态规划表格 dp[pos][rest] 来存储状态。
• 初始化 dp[start][0] = 1，表示初始状态。
• 对于每个剩余汽油量 used，遍历所有城市，更新 dp 数组。

3、代码实现

C++

// 方法1: 记忆化搜索class Solution {private: static constexpr int mod = 1000000007; vector<vector> dp; int dfs(const vector& locations, int pos, int finish, int rest) { if (dp[pos][rest] != -1) { return dp[pos][rest]; } dp[pos][rest] = 0; if (abs(locations[pos] - locations[finish]) > rest) { return 0; } int n = locations.size(); for (int i = 0; i < n; ++i) { if (pos != i) { int cost = abs(locations[pos] - locations[i]); if (cost <= rest) {  dp[pos][rest] += dfs(locations, i, finish, rest - cost);  dp[pos][rest] %= mod; } } } if (pos == finish) { dp[pos][rest] += 1; dp[pos][rest] %= mod; } return dp[pos][rest]; }public: int countRoutes(vector& locations, int start, int finish, int fuel) { dp.assign(locations.size(), vector(fuel + 1, -1)); return dfs(locations, start, finish, fuel); }};

// 方法2: 动态规划class Solution {private: static constexpr int mod = 1000000007;public: int countRoutes(vector& locations, int start, int finish, int fuel) { int n = locations.size(); vector<vector> dp(n, vector(fuel + 1, 0)); dp[start][0] = 1; for (int used = 0; used <= fuel; ++used) { for (int pos = 0; pos < n; ++pos) { if (dp[pos][used] == 0) {  continue; } for (int next = 0; next < n; ++next) {  if (pos == next) { continue;  }  int cost = abs(locations[pos] - locations[next]);  if (used + cost <= fuel) { dp[next][used + cost] += dp[pos][used]; dp[next][used + cost] %= mod;  } } } } int ans = 0; for (int used = 0; used <= fuel; ++used) { ans += dp[finish][used]; ans %= mod; } return ans; }};

Java

// 方法1: 记忆化搜索class Solution { private static final int mod = 1000000007; private int[][] dp; private int dfs(int[] locations, int pos, int finish, int rest) { if (dp[pos][rest] != -1) { return dp[pos][rest]; } dp[pos][rest] = 0; if (Math.abs(locations[pos] - locations[finish]) > rest) { return 0; } int n = locations.length; for (int i = 0; i < n; ++i) { if (pos != i) { int cost = Math.abs(locations[pos] - locations[i]); if (cost <= rest) {  dp[pos][rest] += dfs(locations, i, finish, rest - cost);  dp[pos][rest] %= mod; } } } if (pos == finish) { dp[pos][rest] += 1; dp[pos][rest] %= mod; } return dp[pos][rest]; } public int countRoutes(int[] locations, int start, int finish, int fuel) { dp = new int[locations.length][fuel + 1]; for (int[] row : dp) { Arrays.fill(row, -1); } return dfs(locations, start, finish, fuel); }}

// 方法2: 动态规划class Solution { private static final int mod = 1000000007; public int countRoutes(int[] locations, int start, int finish, int fuel) { int n = locations.length; int[][] dp = new int[n][fuel + 1]; dp[start][0] = 1; for (int used = 0; used <= fuel; ++used) { for (int pos = 0; pos < n; ++pos) { if (dp[pos][used] == 0) {  continue; } for (int next = 0; next < n; ++next) {  if (pos == next) { continue;  }  int cost = Math.abs(locations[pos] - locations[next]);  if (used + cost <= fuel) { dp[next][used + cost] += dp[pos][used]; dp[next][used + cost] %= mod;  } } } } int ans = 0; for (int used = 0; used <= fuel; ++used) { ans += dp[finish][used]; ans %= mod; } return ans; }}

Python

# 方法1: 记忆化搜索class Solution: def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int: mod = 10**9 + 7 n = len(locations) dp = [[-1] * (fuel + 1) for _ in range(n)] def dfs(pos, rest): if dp[pos][rest] != -1: return dp[pos][rest] dp[pos][rest] = 0 if abs(locations[pos] - locations[finish]) > rest: return 0 for i in range(n): if pos != i:  cost = abs(locations[pos] - locations[i])  if cost <= rest: dp[pos][rest] += dfs(i, rest - cost) dp[pos][rest] %= mod if pos == finish: dp[pos][rest] += 1 dp[pos][rest] %= mod return dp[pos][rest] return dfs(start, fuel)

# 方法2: 动态规划class Solution: def countRoutes(self, locations: List[int], start: int, finish: int, fuel: int) -> int: mod = 10**9 + 7 n = len(locations) dp = [[0] * (fuel + 1) for _ in range(n)] dp[start][0] = 1 for used in range(fuel + 1): for pos in range(n): if dp[pos][used] == 0:  continue for next_pos in range(n):  if pos == next_pos: continue  cost = abs(locations[pos] - locations[next_pos])  if used + cost <= fuel: dp[next_pos][used + cost] += dp[pos][used] dp[next_pos][used + cost] %= mod ans = 0 for used in range(fuel + 1): ans += dp[finish][used] ans %= mod return ans

4、复杂度分析

方法一：记忆化搜索（DFS + Memoization）

• 时间复杂度：O(n² * fuel)，其中 n 是城市数量，fuel 是初始汽油量。每个状态 (pos, rest) 只计算一次。
• 空间复杂度：O(n * fuel)，用于存储 dp 数组。

方法二：动态规划（DP）

• 时间复杂度：O(n * fuel)，其中 n 是城市数量。需要填充 dp 表格。
• 空间复杂度：O(n * fuel)，用于存储 dp 数组。

Q16、通过给定词典构造目标字符串的方案数

1、题目描述

给你一个字符串列表 words 和一个目标字符串 target 。words 中所有字符串都 长度相同 。

你的目标是使用给定的 words 字符串列表按照下述规则构造 target ：

• 从左到右依次构造 target 的每一个字符。
• 为了得到 target 第 i 个字符（下标从 0 开始），当 target[i] = words[j][k] 时，你可以使用 words 列表中第 j 个字符串的第 k 个字符。
• 一旦你使用了 words 中第 j 个字符串的第 k 个字符，你不能再使用 words 字符串列表中任意单词的第 x 个字符（x <= k）。也就是说，所有单词下标小于等于 k 的字符都不能再被使用。
• 请你重复此过程直到得到目标字符串 target 。

请注意， 在构造目标字符串的过程中，你可以按照上述规定使用 words 列表中 同一个字符串 的 多个字符 。

请你返回使用 words 构造 target 的方案数。由于答案可能会很大，请对 109 + 7 取余 后返回。

（译者注：此题目求的是有多少个不同的 k 序列，详情请见示例。）

示例 1：

输入：words = [\"acca\",\"bbbb\",\"caca\"], target = \"aba\"输出：6解释：总共有 6 种方法构造目标串。\"aba\" -> 下标为 0 (\"acca\")，下标为 1 (\"bbbb\")，下标为 3 (\"caca\")\"aba\" -> 下标为 0 (\"acca\")，下标为 2 (\"bbbb\")，下标为 3 (\"caca\")\"aba\" -> 下标为 0 (\"acca\")，下标为 1 (\"bbbb\")，下标为 3 (\"acca\")\"aba\" -> 下标为 0 (\"acca\")，下标为 2 (\"bbbb\")，下标为 3 (\"acca\")\"aba\" -> 下标为 1 (\"caca\")，下标为 2 (\"bbbb\")，下标为 3 (\"acca\")\"aba\" -> 下标为 1 (\"caca\")，下标为 2 (\"bbbb\")，下标为 3 (\"caca\")

示例 2：

输入：words = [\"abba\",\"baab\"], target = \"bab\"输出：4解释：总共有 4 种不同形成 target 的方法。\"bab\" -> 下标为 0 (\"baab\")，下标为 1 (\"baab\")，下标为 2 (\"abba\")\"bab\" -> 下标为 0 (\"baab\")，下标为 1 (\"baab\")，下标为 3 (\"baab\")\"bab\" -> 下标为 0 (\"baab\")，下标为 2 (\"baab\")，下标为 3 (\"baab\")\"bab\" -> 下标为 1 (\"abba\")，下标为 2 (\"baab\")，下标为 3 (\"baab\")

示例 3：

输入：words = [\"abcd\"], target = \"abcd\"输出：1

示例 4：

输入：words = [\"abab\",\"baba\",\"abba\",\"baab\"], target = \"abba\"输出：16

提示：

• 1 <= words.length <= 1000
• 1 <= words[i].length <= 1000
• words 中所有单词长度相同。
• 1 <= target.length <= 1000
• words[i] 和 target 都仅包含小写英文字母。

2、解题思路

这是一道典型的动态规划问题。我们可以定义 dp[i][j] 表示使用 words 的前 j 列（即每个单词的前 j 个字符）构造 target 的前 i 个字符的方案数。

1. 预处理字符频率：首先统计每个列（即每个单词的同一位置）中各字符的出现频率，这样可以快速知道在某一列有多少个字符可以匹配 target 的某个字符。
2. 动态规划填充：使用二维数组 dp 来存储子问题的解，dp[i][j] 表示使用前 j 列构造前 i 个字符的方案数。
3. 状态转移：对于每个 target 的字符 target[i]，在每一列 j 中，如果该列有 cnt[j][c] 个字符 c 可以匹配 target[i]，则可以从前 i-1 个字符和前 j-1 列的方案数转移过来。

方法一：记忆化搜索（DFS + Memoization）

• 使用深度优先搜索（DFS）遍历所有可能的构造方案。
• 使用记忆化技术（Memoization）存储已经计算过的子问题结果，避免重复计算。
• 对于每个位置 i 和 j，递归计算使用前 j 列构造前 i 个字符的方案数。

方法二：动态规划（DP）

• 使用动态规划表格 dp[i][j] 来存储状态。
• 初始化 dp[0][j] = 1，表示构造空字符串的方案数为 1。
• 对于每个 target 的字符 target[i] 和每一列 j，更新 dp[i][j] 的值。

3、代码实现

C++

// 方法1: 记忆化搜索class Solution {private: const int mod = 1e9 + 7; long dfs(vector<vector>& dp, vector<vector>& cnt, string& target, int i, int j, int n, int m) { if (j == m) { return 1; // 构造完成 } if (n - i < m - j) { return 0; // 剩余列不足以构造剩余字符 } if (dp[i][j] != -1) { return dp[i][j]; // 已计算过 } long val = cnt[i][target[j] - \'a\'] * dfs(dp, cnt, target, i + 1, j + 1, n, m); // 使用当前列 val += dfs(dp, cnt, target, i + 1, j, n, m); // 不使用当前列 val %= mod; return dp[i][j] = val; }public: int numWays(vector& words, string target) { int n = words[0].length(); vector<vector> cnt(n, vector(26, 0)); // 每列字符频率 for (const auto& s : words) { for (int i = 0; i < n; ++i) { cnt[i][s[i] - \'a\']++; } } int m = target.length(); vector<vector> dp(n, vector(m, -1)); // 记忆化数组 return dfs(dp, cnt, target, 0, 0, n, m); }};

// 方法2: 动态规划class Solution {public: int numWays(vector& words, string target) { const int mod = 1000000007; int n = words.size(); int m = words[0].size(); int t_len = target.length(); vector<vector> freq(m, vector(26, 0)); for (int j = 0; j < m; ++j) { for (int i = 0; i < n; ++i) { char c = words[i][j]; freq[j][c - \'a\']++; } } vector<vector> dp(t_len + 1, vector(m + 1, 0)); for (int j = 0; j <= m; ++j) { dp[0][j] = 1; } for (int i = 1; i <= t_len; ++i) { for (int j = 1; j <= m; ++j) { char c = target[i - 1]; long long ways = dp[i - 1][j - 1] * freq[j - 1][c - \'a\']; ways %= mod; dp[i][j] = (dp[i][j - 1] + ways) % mod; } } return dp[t_len][m] % mod; }};

Java

// 方法1: 记忆化搜索class Solution { private static final int mod = 1000000007; private long dfs(Long[][] dp, int[][] cnt, String target, int i, int j, int n, int m) { if (j == m) { return 1; } if (n - i < m - j) { return 0; } if (dp[i][j] != null) { return dp[i][j]; } long val = cnt[i][target.charAt(j) - \'a\'] * dfs(dp, cnt, target, i + 1, j + 1, n, m); val += dfs(dp, cnt, target, i + 1, j, n, m); val %= mod; return dp[i][j] = val; } public int numWays(String[] words, String target) { int n = words[0].length(); int[][] cnt = new int[n][26]; for (String s : words) { for (int i = 0; i < n; i++) { cnt[i][s.charAt(i) - \'a\']++; } } int m = target.length(); Long[][] dp = new Long[n][m]; return (int) dfs(dp, cnt, target, 0, 0, n, m); }}

// 方法2: 动态规划class Solution { public int numWays(String[] words, String target) { final int mod = 1000000007; int n = words.length; int m = words[0].length(); int t_len = target.length(); int[][] freq = new int[m][26]; for (int j = 0; j < m; j++) { for (int i = 0; i < n; i++) { char c = words[i].charAt(j); freq[j][c - \'a\']++; } } long[][] dp = new long[t_len + 1][m + 1]; for (int j = 0; j <= m; j++) { dp[0][j] = 1; } for (int i = 1; i <= t_len; i++) { for (int j = 1; j <= m; j++) { char c = target.charAt(i - 1); long ways = dp[i - 1][j - 1] * freq[j - 1][c - \'a\']; ways %= mod; dp[i][j] = (dp[i][j - 1] + ways) % mod; } } return (int) (dp[t_len][m] % mod); }}

Python

# 方法1: 记忆化搜索class Solution: def numWays(self, words: List[str], target: str) -> int: mod = 10**9 + 7 n = len(words[0]) cnt = [[0] * 26 for _ in range(n)] for s in words: for i in range(n): cnt[i][ord(s[i]) - ord(\'a\')] += 1 m = len(target) dp = [[-1] * m for _ in range(n)] def dfs(i, j): if j == m: return 1 if n - i < m - j: return 0 if dp[i][j] != -1: return dp[i][j] val = cnt[i][ord(target[j]) - ord(\'a\')] * dfs(i + 1, j + 1) val += dfs(i + 1, j) val %= mod dp[i][j] = val return val return dfs(0, 0)

# 方法2: 动态规划class Solution: def numWays(self, words: List[str], target: str) -> int: mod = 10**9 + 7 n = len(words) m = len(words[0]) t_len = len(target) freq = [[0] * 26 for _ in range(m)] for j in range(m): for i in range(n): c = words[i][j] freq[j][ord(c) - ord(\'a\')] += 1 dp = [[0] * (m + 1) for _ in range(t_len + 1)] for j in range(m + 1): dp[0][j] = 1 for i in range(1, t_len + 1): for j in range(1, m + 1): c = target[i - 1] ways = dp[i - 1][j - 1] * freq[j - 1][ord(c) - ord(\'a\')] ways %= mod dp[i][j] = (dp[i][j - 1] + ways) % mod return dp[t_len][m] % mod

4、复杂度分析

方法一：记忆化搜索（DFS + Memoization）

• 时间复杂度：O(n * m)，其中 n 是 words 中单词的长度，m 是 target 的长度。每个状态 (i, j) 只计算一次。
• 空间复杂度：O(n * m)，用于存储 dp 数组。

方法二：动态规划（DP）

• 时间复杂度：O(n * m)，其中 n 是 words 中单词的长度，m 是 target 的长度。需要填充 dp 表格。
• 空间复杂度：O(n * m)，用于存储 dp 数组。

Q17、网格图中递增路径的数目

1、题目描述

给你一个 m x n 的整数网格图 grid ，你可以从一个格子移动到 4 个方向相邻的任意一个格子。

请你返回在网格图中从 任意 格子出发，达到 任意 格子，且路径中的数字是 严格递增 的路径数目。由于答案可能会很大，请将结果对 109 + 7 取余 后返回。

如果两条路径中访问过的格子不是完全相同的，那么它们视为两条不同的路径。

示例 1：

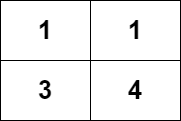
输入：grid = [[1,1],[3,4]]输出：8解释：严格递增路径包括：- 长度为 1 的路径：[1]，[1]，[3]，[4] 。- 长度为 2 的路径：[1 -> 3]，[1 -> 4]，[3 -> 4] 。- 长度为 3 的路径：[1 -> 3 -> 4] 。路径数目为 4 + 3 + 1 = 8 。

示例 2：

输入：grid = [[1],[2]]输出：3解释：严格递增路径包括：- 长度为 1 的路径：[1]，[2] 。- 长度为 2 的路径：[1 -> 2] 。路径数目为 2 + 1 = 3 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• 1 <= grid[i][j] <= 105

2、解题思路

这是一个典型的动态规划问题。我们可以定义 dp[i][j] 表示以格子 (i, j) 为起点的严格递增路径数目。对于每个格子 (i, j)，其 dp[i][j] 的值由其四个相邻格子中数值严格小于当前格子的 dp 值之和加上 1（表示路径长度为 1 的情况）。

1. 记忆化搜索（DFS + Memoization）：使用深度优先搜索遍历所有可能的路径，同时使用记忆化技术存储已经计算过的子问题结果，避免重复计算。
2. 动态规划（DP）：按某种顺序（如数值从小到大）填充 dp 数组，确保在计算 dp[i][j] 时，所有数值更小的相邻格子的 dp 值已经计算完毕。

方法一：记忆化搜索（DFS + Memoization）

• 使用深度优先搜索（DFS）遍历所有可能的路径。
• 使用记忆化技术（Memoization）存储已经计算过的子问题结果，避免重复计算。
• 对于每个格子 (i, j)，递归计算其四个相邻格子中数值严格小于当前格子的 dp 值之和，加上 1。

3、代码实现

C++

class Solution {private: const int MOD = 1\'000\'000\'007; const int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};public: int countPaths(vector<vector>& grid) { int m = grid.size(), n = grid[0].size(); vector<vector> memo(m, vector(n, -1)); // -1 表示没有计算过 auto dfs = [&](this auto&& dfs, int i, int j) -> int { int& res = memo[i][j]; // 注意这里是引用 if (res != -1) // 之前计算过 { return res; } res = 1; for (auto& [dx, dy] : dirs) { int x = i + dx, y = j + dy; if (0 <= x && x < m && 0 <= y && y  grid[i][j]) {  res = (res + dfs(x, y)) % MOD; } } return res; }; long long ans = 0; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { ans += dfs(i, j); } } return ans % MOD; }};

Java

class Solution { private static final int MOD = 1000000007; private static final int[][] dirs = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } }; private int[][] memo; private int dfs(int[][] grid, int i, int j) { if (memo[i][j] != -1) { return memo[i][j]; } int res = 1; for (int[] dir : dirs) { int x = i + dir[0], y = j + dir[1]; if (x >= 0 && x < grid.length && y >= 0 && y < grid[0].length && grid[x][y] > grid[i][j]) { res = (res + dfs(grid, x, y)) % MOD; } } memo[i][j] = res; return res; } public int countPaths(int[][] grid) { int m = grid.length, n = grid[0].length; memo = new int[m][n]; for (int[] row : memo) { Arrays.fill(row, -1); } long ans = 0; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { ans = (ans + dfs(grid, i, j)) % MOD; } } return (int) ans; }}

Python

class Solution: def countPaths(self, grid: List[List[int]]) -> int: MOD = 10**9 + 7 m, n = len(grid), len(grid[0]) memo = [[-1] * n for _ in range(m)] dirs = [(-1, 0), (1, 0), (0, -1), (0, 1)] def dfs(i, j): if memo[i][j] != -1: return memo[i][j] res = 1 for dx, dy in dirs: x, y = i + dx, j + dy if 0 <= x < m and 0 <= y < n and grid[x][y] > grid[i][j]:  res = (res + dfs(x, y)) % MOD memo[i][j] = res return res ans = 0 for i in range(m): for j in range(n): ans = (ans + dfs(i, j)) % MOD return ans

4、复杂度分析

• 时间复杂度：O(m * n)，其中 m 和 n 分别是网格的行数和列数。每个格子仅计算一次。
• 空间复杂度：O(m * n)，用于存储 dp 数组。

Q18、播放列表的数量

1、题目描述

你的音乐播放器里有 n 首不同的歌，在旅途中，你计划听 goal 首歌（不一定不同，即，允许歌曲重复）。你将会按如下规则创建播放列表：

• 每首歌 至少播放一次 。
• 一首歌只有在其他 k 首歌播放完之后才能再次播放。

给你 n、goal 和 k ，返回可以满足要求的播放列表的数量。由于答案可能非常大，请返回对 109 + 7 取余 的结果。

示例 1：

输入：n = 3, goal = 3, k = 1输出：6解释：有 6 种可能的播放列表。[1, 2, 3]，[1, 3, 2]，[2, 1, 3]，[2, 3, 1]，[3, 1, 2]，[3, 2, 1] 。

示例 2：

输入：n = 2, goal = 3, k = 0输出：6解释：有 6 种可能的播放列表。[1, 1, 2]，[1, 2, 1]，[2, 1, 1]，[2, 2, 1]，[2, 1, 2]，[1, 2, 2] 。

示例 3：

输入：n = 2, goal = 3, k = 1输出：2解释：有 2 种可能的播放列表。[1, 2, 1]，[2, 1, 2] 。

提示：

• 0 <= k < n <= goal <= 100

2、解题思路

这是一个典型的动态规划问题。我们可以定义 dp[i][j] 表示听了 i 首歌，其中使用了 j 首不同的歌的方案数。状态转移需要考虑两种情况：

1. 播放一首新歌：从剩余的 n - j + 1 首歌中选择一首。
2. 播放一首旧歌：选择之前播放过的歌，但必须满足至少有 k 首歌在当前歌之前播放过，因此可选歌曲数为 max(j - k, 0)。

方法一：动态规划（DP）

• 初始化 dp[0][0] = 1，表示听了 0 首歌用了 0 首歌的方案数为 1。
• 对于每个 i 和 j ，状态转移方程为：
  • dp[i][j] += dp[i-1][j-1] * (n - j + 1)（播放新歌）
  • dp[i][j] += dp[i-1][j] * max(j - k, 0)（播放旧歌）
• 最终结果为 dp[goal][n]。

方法二：数学方法（容斥原理）

• 使用容斥原理计算所有可能的播放列表，减去不满足条件的播放列表。
• 具体步骤：
  1. 计算所有可能的排列方式。
  2. 减去不满足条件的排列方式（如某些歌未被播放或播放间隔不足）。
  3. 使用组合数学公式计算最终结果。

3、代码实现

C++

// 方法1: 动态规划class Solution {public: int numMusicPlaylists(int n, int goal, int k) { const int MOD = 1\'000\'000\'007; // dp[i][j] 表示听了 i 首歌, 其中使用了 j 首不同的歌的方案数 vector<vector> dp(goal + 1, vector(n + 1, 0)); // 初始化 dp[0][0] = 1, 表示听了 0 首歌用了 0 首歌的方案数为 1 dp[0][0] = 1; // 遍历听歌的数量 for (int i = 1; i <= goal; ++i) { // 遍历使用的不同歌曲数量 for (int j = 1; j <= n; ++j) { // 播放新歌: 从剩下的n - j + 1首歌中选一首 dp[i][j] = (dp[i - 1][j - 1] * (n - j + 1)) % MOD; // 播放旧歌: 从已经播放的j首歌中选一首, 但必须满足间隔 k dp[i][j] = (dp[i][j] + dp[i - 1][j] * max(j - k, 0)) % MOD; } } return dp[goal][n]; // 最终结果 }};

// 方法2: 数学方法 (容斥原理)class Solution {public: int numMusicPlaylists(int n, int goal, int k) { const int MOD = 1\'000\'000\'007; // 计算逆元 auto inv = [&](long x) { long res = 1, p = MOD - 2; while (p > 0) { if (p % 2 == 1) {  res = res * x % MOD; } x = x * x % MOD; p /= 2; } return res; }; long c = 1; for (int x = 1; x <= n - k - 1; ++x) { c = c * -x % MOD; } c = inv(c); // 组合数预处理 long ans = 0; for (int j = 1; j <= n - k; ++j) { ans = (ans + pow(j, goal - k - 1, MOD) * c) % MOD; c = c * (j - (n - k)) % MOD * inv(j) % MOD; } // 乘以 n! (n 的阶乘) for (int j = 1; j  0) { if (exp % 2 == 1) { res = res * base % MOD; } base = base * base % MOD; exp /= 2; } return res; }};

Java

// 方法1: 动态规划class Solution { public int numMusicPlaylists(int n, int goal, int k) { int MOD = 1_000_000_007; long[][] dp = new long[goal + 1][n + 1]; dp[0][0] = 1; // 初始化 for (int i = 1; i <= goal; ++i) { for (int j = 1; j <= n; ++j) { // 播放新歌 dp[i][j] = (dp[i - 1][j - 1] * (n - j + 1)) % MOD; // 播放旧歌 dp[i][j] = (dp[i][j] + dp[i - 1][j] * Math.max(j - k, 0)) % MOD; } } return (int) dp[goal][n]; }}

Python

# 方法1: 动态规划class Solution: def numMusicPlaylists(self, n: int, goal: int, k: int) -> int: MOD = 10**9 + 7 dp = [[0] * (n + 1) for _ in range(goal + 1)] dp[0][0] = 1 # 初始化 for i in range(1, goal + 1): for j in range(1, n + 1): # 播放新歌 dp[i][j] = (dp[i-1][j-1] * (n - j + 1)) % MOD # 播放旧歌 dp[i][j] = (dp[i][j] + dp[i-1][j] * max(j - k, 0)) % MOD return dp[goal][n]

# 方法2: 数学方法 (容斥原理)class Solution: def numMusicPlaylists(self, n: int, goal: int, k: int) -> int: MOD = 10**9 + 7 def inv(x): return pow(x, MOD - 2, MOD) C = 1 for x in range(1, n - k): C *= -x C %= MOD C = inv(C) ans = 0 for j in range(1, n - k + 1): ans = (ans + pow(j, goal - k - 1, MOD) * C) % MOD C = C * (j - (n - k)) % MOD * inv(j) % MOD for j in range(1, n + 1): ans = ans * j % MOD return ans

4、复杂度分析

方法一：动态规划（DP）

• 时间复杂度：O(goal * n)，需要填充 goal 行 n 列的 dp 表格。
• 空间复杂度：O(goal * n)，用于存储 dp 数组。

方法二：数学方法（容斥原理）

• 时间复杂度：O(n²)，需要计算组合数和排列数。
• 空间复杂度：O(n)，用于存储中间计算结果。

Q19、切披萨的方案数

1、题目描述

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： \'A\' （表示苹果）和 \'.\' （表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10⁹ + 7 取余的结果。

示例 1：

输入：pizza = [\"A..\",\"AAA\",\"...\"], k = 3输出：3 解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

示例 2：

输入：pizza = [\"A..\",\"AA.\",\"...\"], k = 3输出：1

示例 3：

输入：pizza = [\"A..\",\"A..\",\"...\"], k = 1输出：1

提示：

• 1 <= rows, cols <= 50
• rows == pizza.length
• cols == pizza[i].length
• 1 <= k <= 10
• pizza 只包含字符 \'A\' 和 \'.\' 。

2、解题思路

这是一个典型的动态规划（DP）问题。我们可以通过以下步骤解决：

1. 预处理苹果数量：计算从每个位置 (i, j) 到右下角的苹果数量，以便快速判断某个区域是否包含苹果。
2. 状态定义：定义 dp[ki][i][j] 表示从 (i, j) 开始，切割 ki 次的方案数。
3. 状态转移：
   • 水平切割：从 (i, j) 向下切割，确保上面的部分有苹果。
   • 垂直切割：从 (i, j) 向右切割，确保左边的部分有苹果。
4. 边界条件：当 ki = 1 时，如果当前区域有至少一个苹果，方案数为 1，否则为 0。

3、代码实现

C++

class Solution {public: int ways(vector& pizza, int k) { int m = pizza.size(), n = pizza[0].size(), mod = 1e9 + 7; // apples[i][j] 表示从 (i, j) 到右下角的苹果数量 vector<vector> apples(m + 1, vector(n + 1)); // dp[ki][i][j] 表示从 (i, j) 开始, 切割 ki 次的方案数 vector<vector<vector>> dp(k + 1, vector<vector>(m + 1, vector(n + 1))); // 预处理苹果数量 for (int i = m - 1; i >= 0; --i) { for (int j = n - 1; j >= 0; --j) { apples[i][j] = apples[i][j + 1] + apples[i + 1][j] - apples[i + 1][j + 1] + (pizza[i][j] == \'A\'); // 初始化: 切割 1 次, 如果当前区域有苹果, 方案数为 1 dp[1][i][j] = apples[i][j] > 0; } } // 动态规划填充 dp 表 for (int ki = 2; ki <= k; ++ki) { for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) {  // 水平方向切割  for (int i2 = i + 1; i2  apples[i2][j]) { dp[ki][i][j] = (dp[ki][i][j] + dp[ki - 1][i2][j]) % mod; }  }  // 垂直方向切割  for (int j2 = j + 1; j2  apples[i][j2]) { dp[ki][i][j] = (dp[ki][i][j] + dp[ki - 1][i][j2]) % mod; }  } } } } return dp[k][0][0]; }};

Java

class Solution { public int ways(String[] pizza, int k) { int m = pizza.length, n = pizza[0].length(), mod = 1_000_000_007; // apples[i][j] 表示从 (i,j) 到右下角的苹果数量 int[][] apples = new int[m + 1][n + 1]; // dp[ki][i][j] 表示从 (i,j) 开始，切割 ki 次的方案数 int[][][] dp = new int[k + 1][m + 1][n + 1]; // 预处理苹果数量 for (int i = m - 1; i >= 0; i--) { for (int j = n - 1; j >= 0; j--) { apples[i][j] = apples[i][j + 1] + apples[i + 1][j] - apples[i + 1][j + 1] + (pizza[i].charAt(j) == \'A\' ? 1 : 0); // 初始化：切割1次，如果当前区域有苹果，方案数为1 dp[1][i][j] = apples[i][j] > 0 ? 1 : 0; } } // 动态规划填充 dp 表 for (int ki = 2; ki <= k; ki++) { for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) {  // 水平方向切割  for (int i2 = i + 1; i2 < m; i2++) { if (apples[i][j] > apples[i2][j]) { dp[ki][i][j] = (dp[ki][i][j] + dp[ki - 1][i2][j]) % mod; }  }  // 垂直方向切割  for (int j2 = j + 1; j2 < n; j2++) { if (apples[i][j] > apples[i][j2]) { dp[ki][i][j] = (dp[ki][i][j] + dp[ki - 1][i][j2]) % mod; }  } } } } return dp[k][0][0]; }}

Python

class Solution: def ways(self, pizza: List[str], k: int) -> int: m, n, mod = len(pizza), len(pizza[0]), 10**9 + 7 # apples[i][j] 表示从 (i,j) 到右下角的苹果数量 apples = [[0] * (n + 1) for _ in range(m + 1)] # dp[ki][i][j] 表示从 (i,j) 开始，切割 ki 次的方案数 dp = [[[0] * (n + 1) for _ in range(m + 1)] for _ in range(k + 1)] # 预处理苹果数量 for i in range(m - 1, -1, -1): for j in range(n - 1, -1, -1): apples[i][j] = apples[i][j + 1] + apples[i + 1][j] - apples[i + 1][j + 1] + (1 if pizza[i][j] == \'A\' else 0) # 初始化：切割1次，如果当前区域有苹果，方案数为1 dp[1][i][j] = 1 if apples[i][j] > 0 else 0 # 动态规划填充 dp 表 for ki in range(2, k + 1): for i in range(m): for j in range(n):  # 水平方向切割  for i2 in range(i + 1, m): if apples[i][j] > apples[i2][j]: dp[ki][i][j] = (dp[ki][i][j] + dp[ki - 1][i2][j]) % mod  # 垂直方向切割  for j2 in range(j + 1, n): if apples[i][j] > apples[i][j2]: dp[ki][i][j] = (dp[ki][i][j] + dp[ki - 1][i][j2]) % mod return dp[k][0][0]

4、复杂度分析

• 时间复杂度 ： O(m×n×k×(m+n))
  • 预处理苹果数量：O(m×n)。
  • 动态规划填充 dp 表：O(k×m×n×(m+n))。
• 空间复杂度 ： O(m×n×k)
  • 存储 apples 表：O(m×n)。
  • 存储 dp 表：O(k×m×n)。

音乐故事