网站导航
> 技术文档 > 【动态规划入门】C语言实现_动态规划题目c语言

【动态规划入门】C语言实现_动态规划题目c语言

网友: 技术文档 2025-09-02 19:12:48

什么是动态规划（Dynamic Programming)

首先我们来看两张经典的图片

在这里插入图片描述

A \"1+1+1+1+1+1+1+1 =？\" A : \"上面等式的值是多少\"B : 计算 \"8!\"A 在上面等式的左边写上 \"1+\" A : \"此时等式的值为多少\"B : quickly\"9!\"A : \"你怎么这么快就知道答案了\"A : \"只要在8的基础上加1就行了\"A : \"所以你不用重新计算因为你记住了第一个等式的值为8!动态规划算法也可以说是 \'记住求过的解来节省时间\'\"

通过这两张图片，我们大致知道动态规划的核心思路就是记住走过的路，从而更快的解决问题。
即——
给定一个问题，我们把它拆分成一个个的子问题，直到子问题可以直接解决，然后将子问题答案保存起来，以减少重复计算，再根据子问题的答案反推，得到原问题解的一种方法就是动态规划（以空间换时间）。

动态规划的解题步骤

  1. dp数组以及下标的含义
  2. 递推公式
  3. dp数组如何初始化
  4. 遍历顺序
  5. 打印数组

一道简单例题加深理解

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
1.i表示现在的位置,dp[i]表示从起点到这个位置的全部方法
2. 从dp[i]的定义可以看出，dp[i] 可以由两个情况推出来。

  • dp[i - 1]。上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶就是dp[i]了。

  • dp[i - 2]。上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶就是dp[i]了。

那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！
所以dp[i] = dp[i - 1] + dp[i - 2] 。

3.初始化
dp[1]=1 dp[2]=2
从dp的定义来看，初始化dp[0]的意义不大

4.从前向后遍历

代码实现

int climbStairs(int n) { int dp[46]={0,1,2,}; if(n<=2) return n; for(int i=3;i<=n;i++) { dp[i]=dp[i-1]+dp[i-2]; } return dp[n];}

通过这个例子，我们已经对动态规划有了初步的解题思路，接下来看一道真正的入门题目

0-1背包问题【二维数组实现】

题目描述

题目描述
现在有一个背包，其容量为N,有n个物品，每个物品所占的空间和价值不同，求该背包所能拥有的最大价值

输入描述
第一行包含两个正整数，第一个整数 M 代表物品的种类，第二个正整数 N，代表背包容量。

第二行包含 M 个正整数，代表每种物品的所占空间。

第三行包含 M 个正整数，代表每种物品的价值。

输出描述
输出一个整数，代表背包的最大价值。

思路描述

解决动态规划问题的五步法：

  1. dp数组以及下标的含义
  2. 递推公式
  3. dp数组如何初始化
  4. 遍历顺序
  5. 打印数组

在本题中：

  1. 首先因为有两个维度需要表示：物品和背包容量，所以使用二维dp。
    【动态规划入门】C语言实现_动态规划题目c语言
    dp[i][j]表示从0到i的物品中任取，放进容量为j的背包中，能得到的最大价值。
  2. 如何得到dp[i][j]的递推公式呢？

求取dp[i][j]有两种情况：

  • 不放物品i：dp[i][j]=dp[i-1][j]
  • 放物品i：dp[i][j]=dp[i-1][j-weight[i]]+value[i]

最终dp[i][j]要等于两种情况中较大的值
递归公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

  1. 如何初始化？
  • 在上面求取递推公式的过程中可以得到：每个元素都是从上方的元素和左上方的元素得到的，所以第一行需要初始化。dp[0][j]的定义是：第0个物品存入不同容量的背包的最大价值。
  • 如果dp[i][j]中j为0的话，无论选取哪个物品最大价值都是0。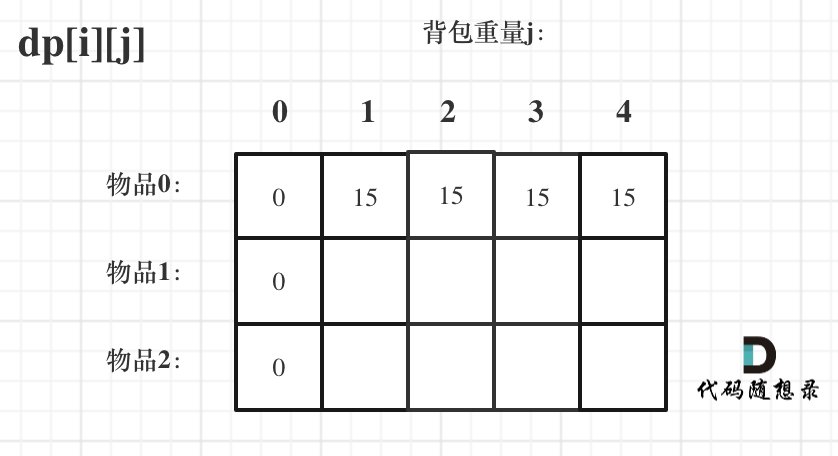
    【动态规划入门】C语言实现_动态规划题目c语言
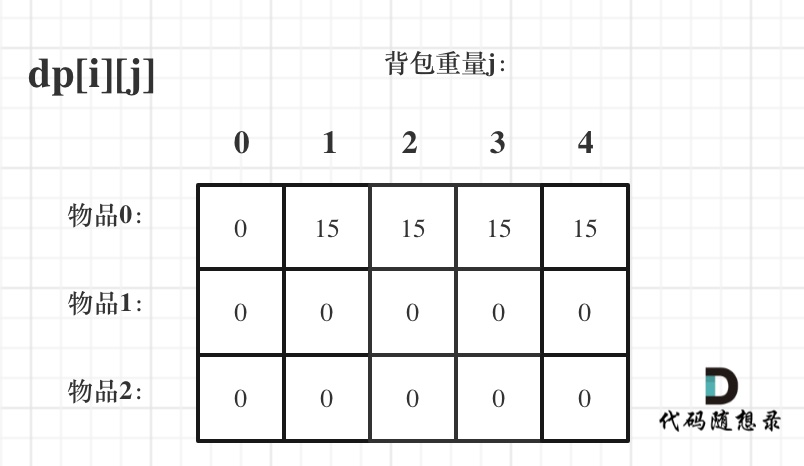
  • 对于其他地方的下标定义任意初始值都可以，因为都是由上方和左上方元素推导出来的，这里初始【动态规划入门】C语言实现_动态规划题目c语言
    化为0。
  1. 遍历顺序
    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。所以先遍历哪个都可以。

代码实现

#include#include//比大小函数int max(int a,int b){ return a>b?a:b;}int main(){int m,n;scanf(\"%d %d\",&m,&n);//动态分配数组，后面需要手动释放int *weight = (int *)malloc(sizeof(int)*m);int *value = (int *)malloc(sizeof(int)*m);for(int i=0;i<m;i++){ scanf(\"%d\",&weight[i]);}for(int i=0;i<m;i++){ scanf(\"%d\",&value[i]);}//初始化二维数组int **dp=(int**)malloc(sizeof(int*)*m); //行for(int i=0;i<m;i++) //列{ dp[i]=(int *)malloc(sizeof(int)*(n+1)); //n+1确保背包容量从0到n //初始化全部元素为0 for(int j=0;j<=n;j++) { dp[i][j]=0; }}//初始化第一行for(int j=weight[0];j<=n;j++){ dp[0][j]=value[0];}//遍历for(int i=1;i<m;i++){ for(int j=0;j<=n;j++) { if(j<weight[i]) { dp[i][j]=dp[i-1][j]; }else { dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]); } }}printf(\"%d\\n\",dp[n-1][n]);for(int i=0;i<m;i++){ free(dp[i]);}free(dp);free(weight);free(value);return 0;}

好的！你学会了二维数组解决0-1背包问题,那么你就可以通过一维数组解决😄 👍 🚀

优化版【一维数组实现】

解题思路

在上述的解题思路中，我们已知dp[i][j]的得到仅依赖于上面一行的元素（上方和左上方），那么我们可以思考，如果直接在上面那行进行计算，用新值覆盖原有的值，即可以将二维数组优化为一维数组。
接下来我们使用动态规划五步法来思考：

  1. dp数组及下标的含义
    实际上，我们是将“物品维度”优化掉，所以一维dp[j]理解为：在容量为j的背包中所能实现的最大价值dp[j]。
  2. 递推公式
    二维数组的递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
    基于去掉物品维度这一理解，在二维数组的递推公式中去掉i即可：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  3. 如何初始化？
  • dp[j]理解为：在容量为j的背包中所能实现的最大价值dp[j]。所以当j为0时，dp[j]=0.
  • dp[j] = max(dp[j], dp[j - weight[i]] + value[i])。dp[j]的得到需要和原有的dp[j]进行比较得最大值，为了不影响结果，我们应该将所有dp[j]赋值为非负得最小值——0.
  1. 遍历顺序
for(int i = 0; i < weight.size(); i++) { // 遍历物品 for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); }}

为什么要先遍历物品，再遍历背包
先遍历物品，考虑物品放进每个背包中的情况，如果先遍历背包，那就导致一个物品可能被使用多次。
为什么要倒叙遍历背包
根据上面：每个dp值的得到依赖于上方和左上方元素和滑动数组的产生，我们可知，在一维数组中，左侧的值是旧值，我们需要使用旧值来得到新值，所以倒序遍历。
在一维数组中，旧值一直存在不会被覆盖，所以正序遍历是合理的。

代码实现

#include#includeint max(int a,int b){ return a>b?a:b;}int main(){int m,n;scanf(\"%d %d\",&m,&n);int *weight = (int *)malloc(sizeof(int)*m);int *value = (int *)malloc(sizeof(int)*m);for(int i=0;i<m;i++){ scanf(\"%d\",&weight[i]);}for(int i=0;i<m;i++){ scanf(\"%d\",&value[i]);}//定义一维数组int *dp=(int*)malloc(sizeof(int)*(n+1)); //初始化for(int i=0;i<=n;i++){ dp[i]=0;}//遍历for(int i=0;i<m;i++){ for(int j=n;j>=weight[i];j--) { dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); }}printf(\"%d\",dp[n]);free(weight); free(value); free(dp);return 0;}
网络标签：

相关问题