保姆级解析：2020 数学建模B题 “穿越沙漠”—— 单人场景 Python 代码 + 动态决策逻辑（超详细！！！）_desert crossing problem

        你是不是也遇到过这种情况：数学建模题思路想得挺顺，一到写代码就卡壳？尤其是像 2020 高教社杯 B 题 “穿越沙漠” 这种规则密密麻麻的题 —— 沙暴日必须停留，矿山当天不能挖矿，村庄买资源贵一倍，还要算负重、算消耗…… 【可恶的小明，能不能不要浪费水啊（无端联想）】光是把这些规则翻译成代码逻辑，就足够让人头大。
        但这道题其实是个 “宝藏题”。从单人已知天气的基础关，到多人动态博弈的进阶关，它几乎涵盖了资源规划、路径优化、不确定性决策的所有核心考点。搞定它，相当于摸透了一大类建模问题的解题套路。
        不过别急，复杂问题总能拆成简单模块。其中第一关和第二关（单人 + 已知天气）是绕不开的基础—— 它们的核心框架（状态设计、动态规划转移）是后面所有关卡的 “骨架”。很多人卡壳，就是因为这两关的代码逻辑没吃透，导致后面更复杂的场景根本无从下手。
        所以这篇文章的重心很明确：把第一关的代码掰开揉碎了讲 —— 从 “怎么定义状态变量” 到 “每天的行动怎么转化成代码逻辑”，连 “沙暴日不能移动”“矿山挖矿多消耗” 这些细节怎么落地，都会给你贴代码片段，最后还会给出可以直接运行的完整的python代码【这还不给主播来个一键三连！！！】
        至于第二题（随机天气）和第三题（多人场景），虽然代码更复杂【实则没招了】（比如随机模拟的参数调优、多人行动的同步判断），但核心思路能从基础关延伸而来。
        不管你是刚入门建模的新手，还是卡在某关的 “老选手”，跟着这篇一步步走，至少能把 “穿越沙漠” 的基础分稳稳拿到手 —— 毕竟，复杂问题的答案，往往就藏在扎实的基础里【加油，你是最棒的！】

一、先吃透这些 “高频规则”，代码才不会写漏

        “穿越沙漠” 的代码 bug 很多源于规则细节遗漏（比如忽略了“矿山到达当天不能挖矿” ）。【就像某些同学常说的，这道题看错了，我本来是会做的啊啊啊】

        先把第一关 / 第二关最核心的规则拎出来，每个规则后面直接标注 “对应代码要处理的逻辑”，后面看代码时可以直接对照：

核心规则（对应题目编号）

规则具体说明

代码需处理的核心逻辑

时间与终点规则（1）

第 0 天从起点出发，需在截止日期（30 天）前到达终点，到达后游戏结束。

1. 用day变量跟踪天数，范围 0-30
2. 到达终点（区域 27）后，终止该状态的后续迭代
3. 最终结果仅保留≤30 天到达终点的状态

资源与负重规则（2）

水和食物以箱为单位，总重量（水 3kg / 箱 + 食物 2kg / 箱）≤1200kg；资源耗尽则失败。

1. 实现is_valid_weight函数，计算总重量并判断是否超标
2. 行动后检查水、食物是否≥0，若＜0 则舍弃该状态

天气基础规则（3）

每天天气为晴朗 / 高温 / 沙暴，全域一致，决定基础消耗量。

1. 用weather列表存储 30 天已知天气
2. 实现get_base_consumption函数，根据当天天气返回对应的基础水 / 食物消耗

行动与天气限制（4）

非沙暴日可移动（相邻区域）或停留；沙暴日必须停留。

1. 用graph字典定义区域相邻关系（仅公共边界相邻）
2. 实现get_possible_actions函数，沙暴日仅保留 “停留” 行动

资源消耗倍数（5）

停留消耗 = 1× 基础消耗量；移动消耗 = 2× 基础消耗量。

1. 行动分支中，停留时cost=1×基础消耗，移动时cost=2×基础消耗
2. 计算行动后剩余资源（当前资源 - 消耗）

起点购买与终点退款（6）

第 0 天起点可按基准价（水 5 元 / 箱，食物 10 元 / 箱）买资源（仅 1 次）；终点剩余资源半价退款。

1. initialize_dp函数遍历第 0 天所有可能的水 / 食物购买组合（受资金和负重限制）
2. 终点计算时加water×5/2 + food×10/2

矿山挖矿规则（7）

矿山可挖矿（基础收益），消耗 = 3× 基础消耗；到达当天不能挖矿；沙暴日可挖矿。

1. 用mines集合标记矿山区域（如 12 号）
2. 实现is_new_arrival函数判断是否新到达（前一天不在该区域），新到达时行动列表剔除 “挖矿”
3. 挖矿时cost=3×基础消耗，资金 + 基础收益

村庄购买规则（8）

村庄可按 2 倍基准价（水 10 元 / 箱，食物 20 元 / 箱）随时购买资源。

1. 用villages集合标记村庄区域（如 15 号）
2. 实现handle_village_purchase函数，计算 2 倍价格购买量（受资金和负重限制），更新资源和资金

二、为什么第一关 / 第二关用动态规划？核心原因在这里

        第一关和第二关的核心条件是 “天气已知 + 单人行动”，这类场景的特性让动态规划成为非常贴合的解决方案：
        首先，天气已知意味着每天的基础消耗量是确定的，资源消耗可以精准计算，不会因不确定性导致状态发散；
        其次，玩家的状态（位置、资源、资金、天数）虽然多样，但始终在有限范围内（比如负重上限限制了资源数量，截止日期限制了天数），且状态之间的转移关系清晰可追溯；【我预判了你所有的预判】
        再者，问题的目标是 “全局最优”—— 比如 “今天多消耗资源提前到达矿山挖矿，可能比单纯节省资源更有利”，这种需要权衡短期消耗与长期收益的场景，恰好适合用动态规划记录每个状态的最优解，通过逐步迭代覆盖所有可能性。
        当然，其他方法（如启发式搜索）在特定场景下也能找到可行解，但动态规划的优势在于能系统地遍历所有可能状态，确保不会遗漏全局最优解，尤其在规则细节密集（如矿山挖矿限制、村庄购买时机）的情况下，能更稳定地处理各种约束条件。因此，针对第一关和第二关的特性，动态规划是兼具严谨性和效率的选择。

三、动态规划核心设计：状态变量与转移逻辑

（1）状态变量怎么定义？少一个要素都不行

        状态变量需要完整包含 “影响未来决策的所有信息”，结合规则对照表，第一关的状态变量必须包含 5 个要素：【这可不像拆电视机，装回去以后，就算手上多出零件电视还可以看】

# 状态变量：(天数, 当前区域, 剩余水(箱), 剩余食物(箱), 剩余资金(元))  

        天数：确保不超过 30 天截止期（对应规则 1）；
        当前区域：决定可移动的相邻区域（对应规则 4 和注 1）；
        剩余水 / 食物：决定能否支撑下一天的行动（对应规则 2）；
        剩余资金：最终需要最大化的目标（受购买、挖矿、退款影响，对应规则 6、7、8）。

在代码中，状态存储结构被优化为三维字典，更高效：

# dp[天数][区域][(水, 食物)] = (最大剩余资金, 前序状态)  
# 例：dp[2][5][(10, 8)] = (8500, (1, 3, 15, 12, \"move_5\"))  
# 表示第2天在区域5，剩余10箱水、8箱食物时，最大资金8500元，前序状态是第1天在区域3，通过移动到5而来  

（2）状态转移逻辑：每天的行动如何生成新状态？

        状态转移是动态规划的 “核心引擎”，本质是 “今天的状态→明天的状态” 的推导过程，严格对应规则中的资源消耗、行动限制等细节。【先有鸡还是先有蛋】用流程图表示如下：

当前状态（day, area, w, f, m）  
    ↓  
根据天气确定可行动作（规则3、4）  
    ↓  
对每个动作（停留/移动/挖矿）：  
    ① 计算资源消耗（规则5、7）  
        - 停留：消耗 = 1×基础消耗（天气决定）  
        - 移动：消耗 = 2×基础消耗  
        - 挖矿：消耗 = 3×基础消耗（需先判断是否新到达矿山，规则7）  
    ② 检查资源是否足够（w-消耗水 ≥0，f-消耗食物 ≥0，规则2）  
    ③ 计算新资金（挖矿+基础收益，购买-成本，规则7、8）  
    ④ 检查负重是否超标（新水×3 + 新食物×2 ≤1200，规则2）  
    ⑤ 若以上均满足，将新状态（day+1, 新区域, 新w, 新f, 新m）存入dp  

四、核心代码解析：从参数到状态转移，逐个拆解

        为了让同学们可以更清晰地把握代码的整体逻辑，我们一起先来梳理一下DesertCrossing类的方法框架。这些方法分工明确，从规则参数初始化到动态规划迭代，再到结果输出，形成了完整的解题闭环。每个方法都对应着 “穿越沙漠” 问题的一个核心环节，具体分工如下：

class DesertCrossing: def __init__(self): # 初始化游戏实例，设置参数存储和状态容器 pass def init_parameters(self): # 初始化游戏基础参数（负重、价格、地图、天气等规则数据） pass def is_valid_weight(self, water, food): # 检查水和食物总重量是否符合负重上限约束 pass def get_base_consumption(self, day): # 根据天数获取当天基础资源消耗量（由天气决定） pass def initialize_dp(self): # 初始化第0天状态（起点购买水和食物的所有可能组合） pass def process_day(self, day): # 处理某天所有状态，生成次日状态（动态规划核心迭代逻辑） pass def get_possible_actions(self, area, weather, day): # 生成当天合法行动（受天气、区域类型约束） pass def is_new_arrival(self, day, area): # 判断是否当天到达某区域（用于矿山\"到达当天不能挖矿\"规则） pass def process_action(self, day, area, water, food, money, prev_state, action): # 处理具体行动，计算资源消耗和新状态 pass def handle_village_purchase(self, next_day, next_area, water, food, money, prev_day, prev_area, prev_water, prev_food, action): # 处理村庄资源购买逻辑（多策略覆盖） pass def update_next_state(self, next_day, next_area, water, food, money, prev_day, prev_area, prev_water, prev_food, action): # 更新次日状态，仅保留同资源组合下资金最多的状态 pass def trace_path(self, day, area, water, food, prev_state): # 回溯最优路径，收集每日状态数据 pass def write_to_excel(self, filename=\"最优路径.xlsx\"): # 将路径数据写入Excel，生成符合要求的结果表格 pass def find_best_result(self): # 从终点状态中筛选最优解（最大资金+最早到达），触发路径回溯和导出 pass def solve(self): # 求解主函数，串联初始化、每日状态处理、最优解查找全流程 pass

        从这个框架能清晰看到：整个解题过程被拆解为 “规则参数化→状态初始化→每日迭代→结果筛选→输出” 五个核心步骤，每个方法专注于解决一个具体问题。比如init_parameters负责将题目规则转化为代码变量，process_day实现动态规划的核心迭代，find_best_result则从海量状态中锁定最优解。
        接下来，我们就按照这个框架的逻辑顺序，逐个解析每个方法的具体实现，看看它们如何将题目中的规则（如 “矿山到达当天不能挖矿”“村庄高价购资源”）转化为可执行的代码逻辑，最终实现从 “思路” 到 “结果” 的完整落地。

关于DesertCrossing类的说明
        这个类是求解问题的核心载体，所有与 “穿越沙漠” 相关的参数、状态和逻辑都通过它实现，主要包含三大模块：
        （1）参数存储：
        用实例变量记录游戏的基础规则（如负重上限、天气序列、地图关系）、特殊区域（矿山、村庄位置）、资源价格等 “硬数据”，这些参数在init_parameters方法中初始化，是后续计算的基础。
        （2）状态管理：
        用三维结构dp[t][u][(w, f)] = (max_money, prev_state)存储动态规划状态：
        t：天数（0~30 天）
        u：当前区域（1~27 号区域）
        (w, f)：剩余水和食物的数量（箱）
        对应的值：该状态下的最大剩余资金，以及前序状态（用于回溯路径）
        （3）核心逻辑方法：
        包含初始化状态（initialize_dp）、每日状态迭代（process_day）、行动处理（process_action）、结果筛选（find_best_result）等方法，实现 “从起点购买资源→每天决策→到达终点筛选最优解” 的完整流程。
        简单说，DesertCrossing类就像一个 “黑盒子”：输入初始参数（如截止日期），调用solve方法后，就能输出最优策略和结果。接下来的函数解析，就是打开这个 “黑盒子”，看它如何一步步实现从规则到结果的转化。

1. __init__：类的构造函数，搭建解题的 “基础框架”

        作为DesertCrossing类的初始化方法，它的核心作用是 “搭架子”—— 为整个解题流程准备必要的存储容器和初始状态，具体做了三件关键事：

（1）加载游戏规则参数

self.init_parameters() 

        这行代码调用init_parameters方法，将题目中的所有 “硬规则”（如负重上限、天气序列、地图关系等）加载到实例变量中（比如self.max_weight存储最大负重，self.weather存储 30 天天气）。这一步是后续所有计算的 “规则基础”，确保代码严格遵循题目设定。

（2）创建动态规划的状态存储容器

self.dp = [defaultdict(dict) for _ in range(self.deadline + 1)] 

        这是整个代码的 “核心数据结构”，用于存储每天的所有可能状态，结构可以拆解为：
        （1）外层列表：按天数（0~30 天）索引，self.dp[day]表示第day天的所有状态；
        （2）中间defaultdict(dict)：按区域（1~27 号区域）索引，self.dp[day][area]表示第day天在area区域的所有状态；
        （3）内层字典：键是(water, food)元组（剩余水和食物的数量），值是(max_money, prev_state)元组（该状态下的最大资金，以及前一天的状态信息，用于回溯路径）。

简单说，self.dp就像一个 “三维表格”，记录了 “第几天、在哪个区域、有多少水和食物” 这三种条件下的最优资金状态，是动态规划迭代的 “主战场”。

（3）初始化结果记录变量

self.best_result = None # 存储最终筛选出的最优解（到达终点的最大资金等信息） self.path_data = [] # 存储最优路径的每日数据（用于后续导出Excel） 

        这两个变量用于 “收尾”—— 在所有状态计算完成后，self.best_result会保存最优解的关键信息（如到达时间、最终资金），self.path_data则记录最优路径的每日详情（每天的区域、资源、资金），为后续输出结果做准备。

小结
        __init__方法通过 “加载规则→创建状态容器→准备结果存储” 三个步骤，为整个解题流程搭好了 “骨架”。它不直接参与计算，而是确保后续方法（如initialize_dp初始化第 0 天状态、process_day迭代每日状态）有统一的 “数据容器” 和 “规则依据”，是代码逻辑连贯性的基础。

2.init_parameters：将游戏规则 “翻译” 成代码变量

        这个方法是整个程序的 “规则数据库”—— 把题目中所有用文字描述的游戏规则（如负重限制、天气消耗、地图关系等），转化为可计算的代码变量。这些变量是后续所有状态计算、行动决策的 “底层依据”，我们按功能模块拆解如下：

（1）基础约束参数：定义游戏的核心限制

self.max_weight = 1200 # 最大负重(千克) self.deadline = 30 # 截止日期(天) self.initial_money = 10000 # 初始资金 self.base_income = 1000 # 挖矿基础收益 

这些参数对应题目最核心的约束条件：
        （1）max_weight：限制总负重不能超过 1200 千克，所有资源携带量必须满足这个约束（由is_valid_weight方法验证）；
        （2）deadline：规定必须在 30 天内到达终点，超过则任务失败；
        （3）initial_money和base_income：分别是初始资金（起点购买资源的预算）和挖矿收益（决定挖矿是否划算的核心指标）。

（2）资源属性参数：定义水和食物的物理属性

self.box_weight = {\"water\": 3, \"food\": 2} # 每箱重量(千克) 

        这是计算负重的关键依据：每箱水重 3kg，每箱食物重 2kg。后续判断 “携带的水和食物是否超重” 时（is_valid_weight方法），会用这个参数计算总重量（water*3 + food*2）。

（3）天气与消耗参数：关联天气和资源消耗的规则

# 不同天气的基础消耗量(箱) self.weather_consumption = { \"晴朗\": {\"water\": 5, \"food\": 7}, \"高温\": {\"water\": 8, \"food\": 6}, \"沙暴\": {\"water\": 10, \"food\": 10} } # 30天的天气序列（索引0-29对应第0天到第29天） self.weather = [ \"高温\", \"高温\", \"晴朗\", \"沙暴\", ..., \"高温\" # 共30天 ] 

这两组参数是 “每日资源消耗” 的核心逻辑：
       （1） weather_consumption：定义了每种天气下的 “基础消耗”（如沙暴天每天消耗 10 箱水、10 箱食物）；
        （2）weather：是具体的天气时间表，决定了第 n 天的消耗基准（比如第 3 天是沙暴，就按沙暴的消耗计算）。
        后续get_base_consumption方法会根据这两个参数，快速获取某天的消耗标准。

（4）价格参数：定义资源购买的成本规则

self.base_price = {\"water\": 5, \"food\": 10} # 基础价格（起点购买价） self.village_price = {\"water\": 10, \"food\": 20} # 村庄价格（是基础价的2倍） 

对应题目中 “资源购买” 的规则：
        （1）起点按基础价格购买（水 5 元 / 箱，食物 10 元 / 箱）；
        （2）村庄购买价格更高（水 10 元 / 箱，食物 20 元 / 箱），这会影响在村庄是否购买资源的决策（handle_village_purchase方法会基于此计算成本）。

（5）地图与区域参数：定义空间关系规则

# 地图：邻接表表示区域连接关系（key是区域，value是相邻区域列表） self.graph = { 1: [2, 25], # 区域1相邻2和25 2: [1, 3], # 区域2相邻1和3 ..., 27: [] # 终点27没有相邻区域（无法移动） } self.start = 1 # 起点区域 self.end = 27 # 终点区域 

这是 “移动规则” 的基础：
        （1）graph定义了每个区域能移动到哪些相邻区域（比如从区域 1 只能去 2 或 25），get_possible_actions方法生成 “移动” 行动时，会从这里获取可选方向；
        （2）start和end标记了流程的起点（初始位置）和终点（目标位置），所有状态最终需到达end才算有效。

（6）特殊区域标记：定义功能区域的规则

self.mines = {12} # 矿山区域（仅区域12是矿山） self.villages = {15} # 村庄区域（仅区域15是村庄） 

这两个集合标记了具有特殊功能的区域：
        （1）mines：矿山区域可执行 “挖矿” 行动（但有 “到达当天不能挖矿” 的限制，由is_new_arrival方法判断）；
        （2）villages：村庄区域可执行 “购买资源” 行动（价格按village_price计算，由handle_village_purchase方法处理）。

小结
        init_parameters的核心价值，是将题目中分散的自然语言规则（如 “沙暴天消耗更多资源”“村庄买东西更贵”），转化为结构化的代码变量。这些变量像 “乐高积木” 一样，支撑起后续所有逻辑（如状态计算、行动判断、资源管理），确保程序严格遵循题目规则。
        后续无论process_day迭代状态，还是find_best_result筛选最优解，本质上都是在这些参数定义的 “规则框架” 内进行计算 —— 修改任何一个参数（比如把deadline改成 25 天），整个策略逻辑都会相应调整，这正是参数化设计的灵活性。

3. is_valid_weight：负重约束的 “守门人”，过滤无效状态

        【不要超重哦~】

        这个方法是动态规划中 “约束检查” 的第一道防线 —— 专门验证当前携带的水和食物总重量是否符合max_weight（1200 千克）的限制。它看似简单，却是确保所有状态 “合法性” 的关键，直接影响后续所有行动的可行性。

（1）核心逻辑：用基础参数计算并判断
        代码只有两行，但每一步都紧扣init_parameters中定义的规则：

total_weight = water * self.box_weight[\"water\"] + food * self.box_weight[\"food\"] return total_weight <= self.max_weight 

        第一步计算总重量：
        用water（水的箱数）乘以每箱水的重量（self.box_weight[\"water\"]，即 3kg），加上food（食物的箱数）乘以每箱食物的重量（self.box_weight[\"food\"]，即 2kg），得到当前携带资源的总重量。
        第二步判断合法性：
        将总重量与最大负重（self.max_weight，1200kg）对比，若小于等于则返回True（合法），否则返回False（超重，无效）。

（2）与其他模块的关联：贯穿全流程的约束检查

        这个方法并非孤立存在，而是在多个关键节点 “站岗”，确保所有状态都符合负重规则：
        （1）初始化阶段（initialize_dp）：在起点购买资源时，会调用它过滤掉超重的（水、食物）组合，避免无效状态进入初始集合；
        （2）行动处理阶段（process_action）：执行移动、停留、挖矿等行动后，计算剩余资源时会再次检查，确保消耗后的资源仍不超重；
        （3）村庄购买阶段（handle_village_purchase）：在村庄补充资源时，会用它验证 “购买后” 的总重量是否合规，防止因多买导致超重。

（3）为什么需要专门的方法？

        有的同学可能会问了：“计算总重量并对比” 很简单，直接写在调用处即可，何必单独封装？主播从三个角度来分析一下：
       （1） 复用性：负重检查需要在多个地方执行（初始化、行动处理、购买资源等），单独封装可避免重复代码；
       （2） 一致性：确保所有地方的负重计算逻辑完全一致（比如都是用box_weight中的参数），避免因手写计算导致的疏漏（比如误将水的重量写成 2kg）；
       （3）可维护性：若题目修改负重规则（比如每箱水重量调整为 4kg），只需修改box_weight参数，无需改动所有调用处的计算逻辑。

小结
        is_valid_weight的核心价值，是将 “最大负重不超过 1200kg” 这个抽象规则，转化为可复用的具体检查逻辑。它像一道 “过滤器”，在状态生成的各个环节拦截超重的无效状态，确保动态规划的dp容器中只保留符合规则的状态，为后续迭代提供可靠的计算基础。
        没有这个 “守门人”，可能会出现 “携带 1000 箱水却不超重” 的荒谬状态，导致整个策略计算失去意义 —— 这正是 “规则落地” 的细节体现：看似简单的约束，也需要严谨的代码来保障。

4.get_base_consumption：天气与消耗的 “翻译器”，提供每日基础消耗标准

        【你总得知道自己付出了多少吧】

        这个方法是连接 “天气规则” 和 “资源消耗” 的核心桥梁 —— 根据具体天数，从预设的天气序列中找到当天天气，再返回该天气对应的基础资源消耗量（水和食物各需多少箱）。它是所有行动（移动、停留、挖矿）资源消耗计算的 “基准发生器”。

（1）核心逻辑：从天数到消耗的两步映射

        代码清晰地实现了 “天数→天气→消耗” 的转化，同时加入了边界保护：

# 第一步：检查天数是否在有效范围（0~29天，共30天） if day = len(self.weather): raise IndexError(f\"天气索引超出范围: day={day}, 有效范围0-{len(self.weather)-1}\") # 第二步：根据天气获取对应消耗 weather = self.weather[day] # 从天气序列中取当天天气（如第3天是“沙暴”） return self.weather_consumption[weather] # 返回该天气的基础消耗（如沙暴天消耗10箱水、10箱食物） 

        （1）边界检查的必要性：
        题目限定截止日期为 30 天，self.weather列表刚好包含 30 天数据（索引 0~29）。如果传入的day超出这个范围（比如 30 或 - 1），直接抛出错误，避免因无效天数导致的错误消耗计算（比如访问不存在的天气数据）。
        （2）映射关系的依据：
        这里的self.weather（天气序列）和self.weather_consumption（天气 - 消耗映射）均来自init_parameters方法，确保与题目规则严格一致（如 “高温天消耗 8 箱水、6 箱食物”）。

（2）与其他模块的关联：所有消耗计算的 “基准源”

这个方法是资源消耗逻辑的 “源头”，被多个核心方法依赖：
        （1）行动处理（process_action）：
        移动、停留、挖矿等行动的消耗都是 “基础消耗的倍数”（如移动消耗 2 倍基础量，挖矿消耗 3 倍）。方法会先调用get_base_consumption(day)获取当天基础消耗，再乘以对应倍数计算实际消耗（例如：沙暴天移动消耗 = 2×10 箱水 = 20 箱水）。
        （2）村庄购买决策（handle_village_purchase）：
        在村庄购买资源时，需要预估未来剩余天数的最大消耗（用于判断该买多少资源）。此时会循环调用get_base_consumption获取未来每天的基础消耗，再累加计算总需求。

小结
        get_base_consumption的核心作用，是将 “第 n 天是什么天气、该消耗多少资源” 这个规则，转化为可靠的、可复用的计算接口。它像一个 “标准化翻译器”，确保所有依赖天气消耗的逻辑（行动处理、资源购买决策等）都能获得一致、正确的基础数据，是资源消耗计算的 “基准保障”。
        没有这个方法，不仅会增加重复代码，更可能因分散的消耗计算逻辑导致规则执行不一致 —— 比如某处忘记判断天数有效性，或误写天气对应的消耗值，最终影响整个策略的准确性。

5. initialize_dp：动态规划的 “起点发生器”，生成第 0 天的所有可能状态

        读者老爷们注意了，来到了重要部分！

        这个方法是整个动态规划流程的 “第一块多米诺骨牌”—— 负责在第 0 天（初始时刻），基于起点的资源购买规则，生成所有合法的初始状态（水、食物、资金的组合），并存入dp容器。这些状态是后续每日迭代（process_day）的基础，直接决定了整个策略计算的覆盖范围。

核心逻辑：在约束内遍历所有可能的初始资源组合

start_area = self.start # 确定起点区域（第0天的初始位置，即区域1） 

        首先锁定初始位置为起点（self.start，即区域 1），所有初始状态都从这里开始。

（1）优化初始水量的遍历范围

max_water = min( self.initial_money // self.base_price[\"water\"], # 资金允许的最大水量（钱够买多少） self.max_weight // self.box_weight[\"water\"] # 负重允许的最大水量（背得动多少） ) 

        这一步是关键优化：通过 “资金上限” 和 “负重上限” 的最小值，限制水量的最大可能值（比如初始资金 10000 元，水 5 元 / 箱，最多买 2000 箱；但负重 1200kg，每箱水 3kg，最多背 400 箱，因此max_water取 400）。
        这样可以避免无效循环（比如遍历 400 箱以上的水，明明买不起或背不动），大幅减少计算量。

（2）遍历水量，计算对应可购买的食物范围

for water in range(0, max_water + 1): remaining_money = self.initial_money - water * self.base_price[\"water\"] # 买水后剩余的钱 if remaining_money < 0: continue # 钱不够，跳过（理论上不会出现，因max_water已限制） # 计算当前水量下，最多能买多少食物 max_food = min( remaining_money // self.base_price[\"food\"], # 剩余资金允许的最大食物量 (self.max_weight - water * self.box_weight[\"water\"]) // self.box_weight[\"food\"] # 剩余负重允许的最大食物量 ) 

        对于每个可能的水量（从 0 到max_water），先计算买水后剩余的钱，再用 “剩余资金” 和 “剩余负重” 两个约束，确定该水量下最多能买多少食物（比如买了 200 箱水后，剩余负重还能背多少食物）。

（3）遍历食物量，筛选合法状态并存入 dp

for food in range(0, max_food + 1): # 双重验证：确保总重量合规（冗余检查，理论上已被max_food限制） if not self.is_valid_weight(water, food): continue # 计算总成本，确保不超初始资金（冗余检查，理论上已被max_food限制） cost = water * self.base_price[\"water\"] + food * self.base_price[\"food\"] if cost > self.initial_money: continue # 计算剩余资金 money = self.initial_money - cost state = (water, food) # 用（水，食物）作为状态的唯一标识 # 只保留该状态下的最大资金（若同一状态已存在，更新为资金更高的） if state not in self.dp[0][start_area] or money > self.dp[0][start_area][state][0]: self.dp[0][start_area][state] = (money, None) # 初始状态无前置状态，prev_state为None 

        对于每个可能的食物量，通过is_valid_weight再次验证总重量（避免极端情况的疏漏），并计算剩余资金。最终将（水，食物）作为状态键，（剩余资金，前置状态）作为值，存入dp[0][start_area]（第 0 天、起点区域的状态容器）。
        这里的核心是 “只保留最大资金”：如果同一（水，食物）组合有多种购买方式（理论上不存在，因价格固定），仅保留资金最高的（实际是唯一值，但逻辑上确保最优）。

（4）与其他模块的关联：为后续迭代提供 “初始燃料”

 initialize_dp生成的状态是整个动态规划的 “起点”，直接决定了后续计算的覆盖范围：
        第 1 天的状态（dp[1]）完全依赖第 0 天的状态（dp[0]），通过process_day(0)迭代生成；
        后续每天的状态（dp[day]）都基于前一天的状态（dp[day-1]），而所有链条的源头都是initialize_dp生成的初始状态。
        如果初始状态覆盖不全（比如漏算了某个可能的水和食物组合），可能会错过全局最优解（例如最优策略需要初始购买 300 箱水，但初始状态没包含这个组合，后续迭代就无法生成对应的路径）。

小结
        initialize_dp的核心价值，是在第 0 天就建立起 “合法状态的全集”—— 既不遗漏任何可能的初始资源组合（确保最优解在其中），又通过约束优化避免无效计算（确保效率）。它像为动态规划 “铺设第一块轨道”，后续的每日迭代（process_day）都将基于这些初始状态向前推进，最终覆盖所有可能的路径和策略。
        没有这个方法，动态规划就成了 “无米之炊”—— 后续的状态迭代将缺乏初始输入，自然无法生成任何有效策略。

6. process_day：动态规划的 “迭代引擎”，实现从当天到次日的状态流转

        【这个是重中之重！！！】

        这个方法是整个解题逻辑的 “核心齿轮”—— 负责将第day天的所有有效状态，通过合法行动转化为第day+1天的新状态，实现动态规划的 “日复一日” 迭代。它像一个 “状态转换器”，确保每个可能的策略路径都能被覆盖，最终积累出到达终点的所有可能状态。

核心逻辑：从当天状态到次日状态的全流程处理

        方法按 “边界检查→状态遍历→行动生成→行动处理” 四步推进，清晰实现了状态的迭代流转：

if day >= self.deadline: return # 超过截止日期，无需处理（避免无效迭代） 

        首先进行边界控制：如果当前天数已达到或超过截止日期（30 天），直接返回，不再处理 —— 因为题目要求必须在 30 天内到达终点，超期的状态已无意义。

（1）进度跟踪与天气获取

current_weather = self.weather[day] # 获取当天天气（用于后续行动约束和消耗计算） if day % 5 == 0: print(f\"处理第 {day} 天，天气: {current_weather}\") # 每5天打印一次进度，方便观察程序运行状态 

        记录当天天气（后续生成行动和计算消耗的关键依据），并通过定期打印进度，让用户了解程序的运行状态（避免长时间无输出导致的 “卡壳” 误解）。

（2）遍历当天所有区域的状态

# 遍历当前天的所有区域（用list转换避免迭代中字典修改导致的错误） for area in list(self.dp[day].keys()): # 遍历该区域的所有状态（(water, food) → (money, prev_state)） for (water, food), (money, prev_state) in list(self.dp[day][area].items()): 

        这是迭代的核心循环：
        （1）外层循环遍历第day天有状态的所有区域（比如第 0 天只有起点区域 1 有状态，后续天数可能扩散到多个区域）；
        （2）内层循环遍历每个区域下的所有状态（即不同的水、食物组合，以及对应的资金和前置状态）。
        使用list(...)转换是为了避免迭代过程中dp[day]被修改（比如新增或删除状态）导致的 “字典大小改变” 错误，确保遍历安全。

（3）过滤已到达终点的状态

if area == self.end: continue # 已到达终点，无需继续行动（终点是最终目标，无需再移动或停留） 

        如果当前状态所在区域是终点（区域 27），则跳过后续处理 —— 因为到达终点后任务已完成，无需再执行任何行动（移动、停留等均无意义）。

（4）生成当天可能的行动

possible_actions = self.get_possible_actions(area, current_weather, day) 

        调用get_possible_actions方法，根据当前区域（是否矿山 / 村庄）、当天天气（是否沙暴）、天数（是否当天到达矿山），生成所有合法的行动（比如沙暴天只能停留，矿山到达当天不能挖矿等）。
        例如：沙暴天在普通区域，possible_actions只能是[\"stay\"]；非沙暴天在非矿山区域，possible_actions包括 “停留” 和 “移动到所有相邻区域”。

（5）处理每个行动，生成次日状态

for action in possible_actions: self.process_action(day, area, water, food, money, prev_state, action) 

        对每个合法行动，调用process_action方法处理：计算该行动的资源消耗（水、食物）、资金变化（挖矿增加收益，购买减少资金）、次日所在区域（移动到新区域或停留在原区域），最终生成第day+1天的新状态，并更新到dp[day+1]中。

与其他模块的关联：串联状态流转的 “中枢”

        process_day是动态规划的 “传送带”，连接了多个核心方法，实现状态的完整迭代：
        （1）依赖get_possible_actions提供合法行动列表（确保行动符合规则）；
        （2）调用process_action处理每个行动，将当天状态转化为次日状态（实现状态转移）；
        （3）最终更新dp容器，为下一天的迭代（process_day(day+1)）提供输入。
        整个动态规划的迭代链条是：initialize_dp（第 0 天）→process_day(0)（生成第 1 天）→process_day(1)（生成第 2 天）→…→process_day(29)（生成第 30 天），而process_day正是这个链条上的每个 “传动齿”。

为什么需要遍历所有状态和行动？

        动态规划的核心思想是 “穷举所有可能，保留最优状态”。process_day的遍历逻辑正是这一思想的体现：
        （1）若漏算某个区域的状态，可能错过最优路径（比如某条绕路经村庄补充资源的策略）；
        （2）若漏算某个合法行动，可能丢失关键策略（比如沙暴天忘记处理 “停留” 行动，导致该天气下的所有状态无法延续）。
        通过 “全区域→全状态→全行动” 的三层遍历，确保所有可能的策略路径都被覆盖，为后续find_best_result筛选最优解提供完整的 “状态池”。

小结
        process_day的核心价值，是实现动态规划的 “每日迭代”—— 以系统化的方式，将当天的所有状态通过合法行动转化为次日状态，确保策略探索的完整性。它像一个 “精密齿轮”，每天转动一次，推动状态池不断扩展，最终覆盖从起点到终点的所有可能路径。
        没有这个 “迭代引擎”，初始状态（initialize_dp生成）就无法向前推进，动态规划也就无法展开，自然无法找到到达终点的最优策略。

7. get_possible_actions：行动合法性的 “裁判”，生成符合规则的行动列表

        【这个也是重点！！！！】

        这个方法是 “行动决策” 的第一道关卡 —— 根据当前区域（是否矿山）、当天天气（是否沙暴）、是否当天到达矿山等条件，筛选出所有符合题目规则的行动（移动、停留、挖矿）。它像一个 “规则过滤器”，确保后续处理的行动都严格遵循游戏设定（如沙暴天不能移动、矿山到达当天不能挖矿）。

核心逻辑：按 “天气→区域类型→到达状态” 三层条件生成行动

代码通过嵌套条件判断，层层过滤出合法行动，逻辑清晰且严格对应题目规则：

（1）沙暴天：只能停留，禁止移动

if weather == \"沙暴\": # 沙暴天无论在什么区域，都不能移动，只能停留（题目规则） if area in self.mines: # 若当前在矿山区域 # 判断是否当天到达矿山（前一天不在该区域） is_new_arrival = self.is_new_arrival(day, area) if is_new_arrival:  actions.append(\"stay\") # 到达当天只能普通停留（不能挖矿） else:  actions.append(\"stay\") # 非当天到达，可普通停留  actions.append(\"mine\") # 非当天到达，可挖矿（沙暴天允许挖矿，仅限制移动） else: actions.append(\"stay\") # 普通区域，沙暴天只能停留 

        沙暴天的核心约束是 “禁止移动”，因此行动列表中不会出现 “move_xxx”。仅在矿山区域且非当天到达时，才允许 “挖矿”（题目未禁止沙暴天挖矿，仅限制移动）。

（2）非沙暴天：可移动 + 停留，矿山区域需额外判断

else: # 天气为晴朗或高温（非沙暴） # 第一步：添加移动到相邻区域的行动（非沙暴天允许移动） for neighbor in self.graph[area]: actions.append(f\"move_{neighbor}\") # 行动格式为\"move_目标区域\"（如\"move_2\"表示移动到区域2） # 第二步：添加停留相关行动（非沙暴天可停留，矿山区域有额外限制） if area in self.mines: # 若当前在矿山区域 is_new_arrival = self.is_new_arrival(day, area) # 判断是否当天到达 if is_new_arrival:  actions.append(\"stay\") # 到达当天只能普通停留（不能挖矿） else:  actions.append(\"stay\") # 非当天到达，可普通停留  actions.append(\"mine\") # 非当天到达，可挖矿 else: actions.append(\"stay\") # 普通区域，非沙暴天可直接停留 

        非沙暴天的核心是 “允许移动”，因此首先遍历当前区域的所有相邻区域（从self.graph获取），生成 “move_目标区域” 形式的行动（如区域 1 的相邻区域是 2 和 25，因此生成 “move_2”“move_25”）。
        对于停留行动，同样需判断是否在矿山且是否当天到达 —— 这是为了遵守 “矿山到达当天不能挖矿” 的规则（只能普通停留）。

关键依赖：is_new_arrival方法的 “到达状态判断”

is_new_arrival = self.is_new_arrival(day, area) 

        这个判断是矿山行动的核心约束：通过检查 “前一天是否在该区域”，确定是否为 “当天到达”。若为当天到达，即使在矿山也不能挖矿，只能停留；若非当天到达，则可选择停留或挖矿。
        这一步直接关联is_new_arrival方法，确保 “矿山到达当天不能挖矿” 的规则被严格执行。

与其他模块的关联：行动处理的 “源头”

        get_possible_actions生成的行动列表是process_day迭代的关键输入：
        process_day在遍历当天状态后，调用本方法获取合法行动，再通过process_action处理每个行动，生成次日状态；
        若本方法遗漏了合法行动（如非沙暴天忘记添加移动行动），会导致策略路径不完整（比如无法到达某个关键区域）；
        若误加了非法行动（如沙暴天允许移动），会导致process_action生成无效状态（比如沙暴天移动消耗资源但实际不允许，最终路径违规）。

小结
        get_possible_actions的核心价值，是将题目中分散的行动约束（如 “沙暴天不能移动”“矿山到达当天不能挖矿”）转化为可执行的代码逻辑，生成精准的合法行动列表。它像一个 “行动菜单”，只提供符合规则的选项，确保后续的状态转移（process_action）都在规则框架内进行。
        没有这个 “裁判”，行动处理可能会出现违规操作（如沙暴天移动、矿山当天挖矿），导致整个策略计算失去意义 —— 这正是 “规则落地” 在行动层面的关键体现。

8. is_new_arrival：区域到达状态的 “检测器”，判断是否当天首次进入某区域

        【小模块大作用！】

        这个方法是矿山行动规则的 “核心开关”—— 专门判断当前是否为 “当天首次到达某区域”，直接决定了在矿山区域能否执行 “挖矿” 行动（题目规则：矿山到达当天不能挖矿，需至少停留 1 天后才能挖矿）。它通过对比前后两天的状态，精准识别 “新到达” 状态，为行动合法性提供关键依据。

核心逻辑：用前后两天的状态对比判断到达状态

代码通过区分 “第 0 天” 和 “其他天数”，用简洁的逻辑实现了到达状态的判断：

（1）第 0 天的特殊处理

if day == 0: return area == self.start # 第0天只有起点是初始位置 

        第 0 天是初始时刻，所有状态都从起点（self.start，即区域 1）开始 —— 此时：
        （1）若area是起点（区域 1），说明是初始位置，并非 “当天到达”（因为从一开始就在这里），因此返回False；
        （2）若area是其他区域（理论上第 0 天不会有状态），则返回True（但实际中第 0 天的dp只包含起点，因此这种情况不会出现）。
        这一步确保了初始位置的特殊性：起点在第 0 天不属于 “新到达”，因为不是 “当天进入”，而是初始就在那里。

（2）第 1 天及以后：通过前一天状态判断

# 检查前一天是否在该区域有任何状态 return len(self.dp[day-1].get(area, {})) == 0 

对于第 1 天及以后（day ≥ 1），判断逻辑基于 “前一天的状态记录”：
        self.dp[day-1].get(area, {})：获取前一天（day-1）该区域的所有状态（若不存在则返回空字典）；
        len(...) == 0：若前一天该区域没有任何状态（长度为 0），说明当天是第一次进入该区域，返回True（新到达）；
        反之，若前一天该区域有状态（比如前一天就停留在这），说明不是当天首次到达，返回False。

关键价值：为矿山行动提供精准约束

        这个方法的核心作用，是支撑 “矿山到达当天不能挖矿” 的规则 —— 在get_possible_actions中，当当前区域是矿山时，会调用is_new_arrival判断：
        （1）若返回True（当天到达）：只能添加 “stay” 行动（不能挖矿）；
        （2）若返回False（非当天到达）：可添加 “stay” 和 “mine” 两种行动（允许挖矿）。
        例如：第 5 天进入矿山区域 12，is_new_arrival(5, 12)会检查第 4 天区域 12 是否有状态。若第 4 天没有，则返回True，第 5 天只能在矿山停留；第 6 天再检查时，因第 5 天已有状态，返回False，第 6 天可选择挖矿。

与其他模块的关联：行动规则的 “状态传感器”

is_new_arrival是get_possible_actions的关键依赖，直接影响矿山区域的行动生成：
        若该方法判断错误（比如误将 “非新到达” 判定为 “新到达”），会导致矿山无法挖矿（即使已停留超过 1 天），错过潜在收益；
        若反之（误将 “新到达” 判定为 “非新到达”），会导致当天到达矿山就允许挖矿，违反题目规则，生成无效策略。
        它像一个 “状态传感器”，通过dp容器中存储的历史状态，为行动规则提供实时的 “到达状态” 数据。

小结
        is_new_arrival的核心价值，是通过对比前后两天的状态记录，精准识别 “当天首次到达某区域” 的状态，为矿山行动的合法性提供 “开关信号”。它像一个 “规则执行器”，确保 “矿山到达当天不能挖矿” 这一约束被严格遵守，是行动生成逻辑中不可或缺的细节保障。
        没有这个 “检测器”，矿山行动的判断就会失去依据，可能出现 “当天到达即挖矿” 的违规策略，导致整个计算结果不符合题目要求 —— 这正是代码对规则细节的严谨落地。

9. process_action：行动到状态的 “转换器”，计算行动后的次日状态

       【 接下来这一步很关键，同学们别睡着了！！！】

        这个方法是动态规划状态转移的 “具体执行者”—— 针对当天的每个合法行动（移动、停留、挖矿），计算资源消耗、资金变化和下一区域，生成第day+1天的新状态。它像一个 “状态计算器”，严格按照行动类型和规则，将当前状态转化为符合约束的次日状态，是连接 “当天状态” 与 “次日状态” 的核心纽带。

核心逻辑：按行动类型计算消耗，生成合规的次日状态

方法按 “边界检查→行动解析→消耗计算→有效性验证→状态更新” 的流程，完整实现了行动到状态的转化：

（1）边界控制：确保不超截止日期

next_day = day + 1 # 行动后进入的天数 if next_day > self.deadline: return # 超过截止日期，无需处理（生成的状态无意义） 

        首先计算行动后的天数（next_day），若超过截止日期（30 天），直接返回 —— 因为题目要求必须在 30 天内到达终点，超期的状态无需记录。

（2）获取基础数据：天气与基础消耗

current_weather = self.weather[day] # 当天天气（已在process_day中获取，此处可复用） base_consumption = self.get_base_consumption(day) # 当天基础消耗量（水、食物的基准值） 

        调用get_base_consumption获取当天的基础消耗（由天气决定），这是计算不同行动消耗的基准（如移动消耗 2 倍基础量，挖矿消耗 3 倍）。

（3）按行动类型计算消耗、区域和资金

这是方法的核心，针对 “移动”“停留”“挖矿” 三种行动，分别计算资源消耗、下一区域和资金变化：
        （1）移动行动（action.startswith(\"move\")）：

next_area = int(action.split(\"_\")[1]) # 从行动名中提取目标区域（如\"move_2\"→区域2） water_cost = 2 * base_consumption[\"water\"] # 移动消耗2倍基础水量 food_cost = 2 * base_consumption[\"food\"] # 移动消耗2倍基础食物量 new_money = money # 移动不影响资金 

        移动的核心规则：消耗是基础量的 2 倍（题目规则 5），区域变为目标相邻区域（从行动名提取），资金不变。
        （2）停留行动（action == \"stay\"）：

next_area = area # 停留时区域不变 water_cost = base_consumption[\"water\"] # 停留消耗1倍基础水量 food_cost = base_consumption[\"food\"] # 停留消耗1倍基础食物量 new_money = money # 停留不影响资金 

        停留的核心规则：消耗是基础量的 1 倍（规则 5），区域不变，资金不变。
        （3）挖矿行动（action == \"mine\"）：

next_area = area # 挖矿时区域不变（在矿山原地挖矿） water_cost = 3 * base_consumption[\"water\"] # 挖矿消耗3倍基础水量 food_cost = 3 * base_consumption[\"food\"] # 挖矿消耗3倍基础食物量 new_money = money + self.base_income # 挖矿获得基础收益（1000元/天） 

        挖矿的核心规则：消耗是基础量的 3 倍（规则 7），区域不变，资金增加基础收益（self.base_income）。

（4）有效性验证：资源足够且负重合规

# 计算行动后剩余的水和食物 new_water = water - water_cost new_food = food - food_cost # 检查资源是否足够（不能为负） if new_water < 0 or new_food < 0: return # 资源不足，该状态无效，不记录 # 检查剩余资源的负重是否合规 if not self.is_valid_weight(new_water, new_food): return # 超重，该状态无效，不记录 

        这是关键的约束检查：
        （1）资源不能为负（否则视为 “资源耗尽失败”，规则 2）；
        （2）剩余资源的总重量不能超过最大负重（规则 2）。
        任何一项不满足，都直接丢弃该状态，不进入下一步。

（5）更新次日状态：区分村庄与非村庄

if next_area in self.villages: # 若下一区域是村庄（区域15） # 调用村庄购买逻辑（可补充资源） self.handle_village_purchase(next_day, next_area, new_water, new_food, new_money, day, area, water, food, action) else: # 非村庄区域 # 直接更新状态（无需购买） self.update_next_state(next_day, next_area, new_water, new_food, new_money, day, area, water, food, action) 

        根据下一区域是否为村庄，分两种处理方式：
        （1）村庄区域：调用handle_village_purchase，允许在消耗后补充资源（按 2 倍价格购买），生成更多可能的状态；
        （2）非村庄区域：直接调用update_next_state，将消耗后的状态存入dp[next_day][next_area]。

与其他模块的关联：状态转移的 “执行器”

        process_action是动态规划迭代的 “最终执行者”，连接了多个核心环节：
        （1）依赖get_base_consumption提供基础消耗数据，确保消耗计算符合天气规则；
        （2）依赖is_valid_weight验证负重，确保状态合规；
        （3）调用handle_village_purchase或update_next_state，将有效状态写入dp容器，为次日迭代提供输入。
        如果这个方法出现逻辑错误（比如移动消耗算成 3 倍基础量），会导致所有行动的状态转移错误，最终影响最优解的准确性。

小结
        process_action的核心价值，是将抽象的 “行动” 转化为具体的 “次日状态”—— 通过严格计算消耗、验证约束、区分场景（村庄 / 非村庄），确保每个行动都能生成合规且有效的新状态。它像动态规划的 “生产车间”，每天将输入的状态（原材料）通过行动（加工流程）转化为输出的状态（产品），推动整个策略计算向前迭代。
        没有这个 “转换器”，get_possible_actions生成的行动列表就无法转化为实际的状态，动态规划的迭代链条会断裂，自然无法生成到达终点的路径。

10. handle_village_purchase：村庄资源补充的 “决策中心”，生成最优购买策略

        【正如一年级是人生中最关键的时期，二年级是打基础的时候，三年级...

        所以，这个很重要！！！】

        这个方法是村庄区域的 “专属处理器”—— 当次日状态位于村庄（区域 15）时，基于当前资源、资金和未来需求，生成所有可能的资源购买策略（不买、只买水、只买食物、同时买），并更新为合法的次日状态。它像一个 “资源补给站”，在高价购买的约束下（村庄价格是基准价的 2 倍），平衡 “补充资源避免中途耗尽” 和 “节省资金提高最终收益” 的矛盾，确保村庄的资源补充决策最优。

核心逻辑：基于未来需求的精细化购买决策

方法按 “需求预估→购买量计算→策略生成” 的流程，分步骤生成符合约束的购买方案，既不盲目购买（避免资金浪费），也不遗漏必要补充（避免资源不足）：
（1）预估未来最大资源需求：购买决策的 “基准线”

remaining_days = self.deadline - next_day + 1 # 从次日到截止日的剩余天数 max_future_water = 0 max_future_food = 0 # 按每天“移动”的最大消耗（2倍基础消耗）估算未来需求（最保守的情况） for d in range(next_day, min(self.deadline, len(self.weather))): wc = self.get_base_consumption(d) # 获取未来某天的基础消耗 max_future_water += 2 * wc[\"water\"] # 移动消耗2倍水量 max_future_food += 2 * wc[\"food\"] # 移动消耗2倍食物量 

        这是购买决策的核心依据：
        （1）按 “每天都在移动” 计算最大消耗（2 倍基础消耗），确保预估的需求是 “最坏情况”（避免低估需求导致后续资源不足）；
        （2）遍历从次日到截止日的所有天数，累加总需求，作为判断 “是否需要购买” 的基准。

（2）计算需要补充的资源量：明确购买目标

needed_water = max(0, max_future_water - water) # 需补充的水量（当前水不足未来需求时） needed_food = max(0, max_future_food - food) # 需补充的食物量（当前食物不足未来需求时） 

        如果当前资源（行动后剩余的water和food）已超过未来最大需求，needed_water或needed_food为 0，无需购买对应资源；否则，差值即为需要补充的量（避免买多了浪费资金和负重）。

（3）计算可购买的最大量：受资金、负重和需求三重约束

        以 “只买水” 为例，计算最大可购买量：

max_buy_water = min( needed_water, # 不超过实际需求（买多了没用） money // self.village_price[\"water\"], # 不超过资金上限（买不起的不考虑） # 不超过剩余负重（总负重-当前食物重量后，能承载的额外水量） (self.max_weight - food * self.box_weight[\"food\"]) // self.box_weight[\"water\"] - water ) 

        这个计算确保购买的水 “买得起、背得动、刚好够”，避免无效购买（比如资金够但背不动，或买了远超需求的水）。

（4）生成四种购买策略：覆盖所有可能的最优解

方法通过四种策略覆盖所有合理的购买决策，确保不遗漏潜在的最优解：
        策略 1：不购买

self.update_next_state(next_day, next_area, water, food, money, ...) 

        当当前资源已足够支撑到终点，或资金不足 / 负重不够时，不购买是最优选择（避免花高价买不需要的资源）。

        策略 2：只买水

if needed_water > 0 and max_buy_water > 0: buy_water = min(needed_water, max_buy_water) new_m = money - buy_water * self.village_price[\"water\"] # 扣除买水成本 self.update_next_state(..., water + buy_water, food, new_m, ...) 

        当仅缺水、不缺食物时，单独补充水（比如未来高温天多，水量消耗大）。

        策略 3：只买食物

if needed_food > 0: max_buy_food = min(needed_food, money//self.village_price[\"food\"], ...) # 类似水的约束 if max_buy_food > 0: new_f = food + max_buy_food new_m = money - max_buy_food * self.village_price[\"food\"] self.update_next_state(..., water, new_f, new_m, ...) 

        当仅缺食物、不缺水时，单独补充食物（比如未来晴朗天多，食物消耗大）。

        策略 4：同时买水和食物

if needed_water > 0 and needed_food > 0 and max_buy_water > 0: remaining_money_after_water = money - max_buy_water * self.village_price[\"water\"] max_buy_food = min(needed_food, remaining_money_after_water//self.village_price[\"food\"], ...) if max_buy_food > 0: self.update_next_state(..., water + max_buy_water, food + max_buy_food, ...) 

        当水和食物都缺时，先买水（按最大需求），再用剩余资金买食物，确保优先级高的资源先得到补充。

关键细节：行动名标记与状态追溯

        每种策略的行动名都会添加后缀（如_buy_water _buy_both），例如原行动是 “move_15”（移动到村庄），购买水后行动名变为 “move_15_buy_water”。这一标记在后续trace_path回溯路径时，能清晰区分不同的购买决策，便于验证策略合理性。

与其他模块的关联：资源补充的 “关键节点”

        handle_village_purchase是村庄区域状态生成的核心，直接影响后续策略的可行性：
        （1）依赖get_base_consumption获取未来天气的消耗数据，确保需求预估准确；
        （2）依赖update_next_state将购买后的状态存入dp，为次日迭代提供 “补充资源后的新状态”；
        其决策直接影响最终资金（买得越多，资金越少，但可能避免中途资源耗尽），是平衡 “短期消耗” 与 “长期收益” 的关键。

为什么需要多种购买策略？

        村庄的特殊性在于 “高价购买”（2 倍价格），这意味着 “买什么、买多少” 的决策对最终结果影响极大：
        少买可能导致后续资源不足，任务失败；
        多买会浪费资金，降低最终收益；
        只买需要的资源（水或食物）可能比全买更划算（比如未来食物消耗少，无需补充）。
        四种策略的覆盖确保了所有合理决策都被纳入动态规划，避免因 “漏算某类购买” 而错过最优解。

小结
        handle_village_purchase的核心价值，是在村庄这一 “资源补给节点”，通过精细化的需求预估和约束计算，生成所有可能的购买策略，平衡 “高价购买” 与 “资源保障” 的矛盾。它像一个 “精打细算的补给官”，在有限的资金和负重下，确保每一分钱都花在刀刃上，为后续到达终点提供必要的资源支撑，同时最大限度保留资金。
        没有这个方法，村庄的资源补充就会被简化（比如要么全买要么不买），可能导致要么资源不足失败，要么资金浪费收益降低，无法实现真正的最优策略。

11. update_next_state：动态规划的 “状态过滤器”，只保留最优状态

        【著名的作家鲁迅说过：知道如何保留最优状态很重要！！！】

        这个方法是次日状态存入dp容器的 “最后一道关卡”—— 负责将经过行动处理（或村庄购买）后的有效状态，按 “同一资源组合下保留最大资金” 的原则存入dp[next_day][next_area]。它像一个 “优化器”，通过过滤冗余状态（同一资源组合下资金较低的），确保dp容器中只保留有价值的状态，既减少计算量，又为后续迭代和最优解筛选提供可靠的 “状态池”。

核心逻辑：保留同一资源组合下的最大资金状态

方法通过 “约束验证→状态定义→最优筛选” 三步，实现状态的高效存储：

（1）最后一道约束验证：确保状态合法

if not self.is_valid_weight(water, food): return # 负重超标，该状态无效，不存入dp 

        虽然在process_action或handle_village_purchase中已做过负重检查，但这里再次验证（冗余检查），避免因计算疏漏导致的无效状态进入dp（比如村庄购买后资源重量计算错误）。

（2）定义状态的唯一标识：资源组合为键

state = (water, food) # 用（水，食物）作为状态的唯一标识 

        在动态规划中，“状态” 的核心是 “资源组合”—— 对于同一区域（next_area）和天数（next_day），只要水和食物的数量相同，就视为 “同一状态”，无论通过哪条路径到达。这一设计确保了状态的唯一性，为后续 “保留最优” 提供判断基准。

（3）记录前序状态：为路径回溯做准备

previous_state = (prev_day, prev_area, prev_water, prev_food, action) 

        存储前序状态（前一天的天数、区域、资源和执行的行动），用于后续trace_path回溯路径时，能从终点倒推回起点，还原完整的策略路径（比如 “第 5 天在区域 15 买了水，是因为第 4 天从区域 10 移动过来”）。

（4）核心筛选：只保留资金最高的状态

# 若该状态不存在，直接存入 if state not in self.dp[next_day][next_area]: self.dp[next_day][next_area][state] = (money, previous_state) else: # 若已存在，只保留资金更高的状态 current_max_money = self.dp[next_day][next_area][state][0] if money > current_max_money: self.dp[next_day][next_area][state] = (money, previous_state) 

这是动态规划 “最优子结构” 的关键体现：
        对于同一（水，食物）组合（即同一状态），资金更高的显然更优（因为最终目标是最大化资金）；
        即使两条不同路径到达同一状态，只需保留资金更高的那条 —— 因为从该状态出发，后续迭代能产生的最优解只可能来自资金更高的状态（资金低的状态不可能在后续超过资金高的）。

与其他模块的关联：状态存储的 “统一入口”

        update_next_state是所有有效状态进入dp容器的唯一入口，被两个核心方法调用：
        （1）process_action处理非村庄区域的行动后，调用它存入状态；
        （2）handle_village_purchase处理村庄购买后，调用它存入不同购买策略的状态。
        这种 “统一入口” 设计确保了所有状态的存储逻辑一致（都遵循 “保留最大资金” 原则），避免因分散存储导致的状态混乱（比如某处忘记比较资金，保留了低效状态）。

为什么必须 “只保留最大资金”？

        动态规划的效率和准确性依赖于 “状态精简”：
        （1）若不筛选，同一（水，食物）组合可能对应多个资金值，dp容器会急剧膨胀（比如 1000 种资源组合，每种对应 5 种资金，总状态量增加 5 倍），导致后续迭代效率骤降；
        （2）资金低的状态在后续迭代中不可能产生更优解（因为任何行动对资金的影响是固定的，资金低的起点无法超过资金高的起点），保留它们只会浪费计算资源。
        通过筛选，dp容器中的状态量被大幅压缩，同时确保每个状态都是 “当前最优”，为后续process_day迭代和find_best_result筛选最优解奠定基础。

小结
        update_next_state的核心价值，是作为动态规划的 “状态优化器”—— 通过统一的存储逻辑，只保留同一资源组合下资金最高的状态，既保证dp容器的精简高效，又确保所有状态都是 “最优子结构”，为最终找到全局最优解提供可靠的状态基础。
        没有这个 “过滤器”，dp容器会被大量冗余状态充斥，不仅降低计算效率，还可能因保留低效状态导致后续迭代错过最优解，整个动态规划的严谨性将大打折扣。

12. trace_path：最优路径的 “时光回溯机”，还原从终点到起点的完整历程

        【妈妈，我从哪里来？？？

        想知道啊，我教你呀！】

        这个方法是路径还原的 “核心工具”—— 从最优解的终点状态出发，通过递归追溯前序状态（prev_state），一步步倒推回起点（第 0 天），同时收集每天的关键数据（日期、区域、资金、资源），最终形成完整的最优路径记录。它像一个 “逆向导航”，将动态规划dp容器中分散存储的状态串联成一条可追溯的策略路径，为后续导出 Excel 提供结构化数据。

核心逻辑：递归回溯，从终点倒推至起点

方法通过 “当前状态记录→递归追溯前序→终止条件判断” 的递归逻辑，完整还原路径：

（1）记录当前状态数据

# 获取当前状态的资金（从dp中提取该状态对应的资金） current_money = self.dp[day][area].get((water, food), [0, None])[0] # 避免同一日期重复记录（最优路径中每天只需要一条记录） if not any(item[\'日期\'] == day for item in self.path_data): self.path_data.append({ \'日期\': day, \'所在区域\': area, \'剩余资金数\': current_money, \'剩余水量\': water, \'剩余食物量\': food }) 

        这一步将当前状态的关键信息（日期、区域、资金、水、食物）存入self.path_data列表，用于后续导出 Excel。
        核心细节是 “避免重复记录”：由于递归回溯可能通过不同路径关联到同一天（理论上最优路径中不会出现），通过检查path_data中是否已有该日期的记录，确保每天只保留一条数据（最优路径上的状态）。

（2）递归追溯前序状态

if prev_state and day > 0: # 若存在前序状态且不是起点（第0天） # 解析前序状态：前一天的天数、区域、资源和执行的行动 prev_day, prev_area, prev_water, prev_food, action = prev_state # 获取前序状态的前序（用于继续回溯） prev_state_data = self.dp[prev_day][prev_area].get((prev_water, prev_food), [0, None]) # 递归调用，追溯前一天的状态 self.trace_path(prev_day, prev_area, prev_water, prev_food, prev_state_data[1]) 

这是回溯的核心：
        （1）prev_state是当前状态的 “来源”（前一天的状态信息），包含前一天的天数、区域、资源和行动（如 “第 5 天在区域 15，来自第 4 天从区域 10 移动过来”）；
        （2）通过递归调用trace_path，从当前天（day）倒推到前一天（prev_day），再到前前一天，直到追溯到第 0 天（起点）；
        （3）终止条件：当prev_state为None（起点状态没有前序）或day == 0（已到起点）时，递归终止。

与其他模块的关联：路径还原的 “执行者”

        trace_path是连接 “最优解” 与 “路径展示” 的关键，其运行依赖两个核心模块：
        （1）依赖dp容器存储的前序状态（prev_state）：update_next_state在存储状态时记录了previous_state，为回溯提供了 “导航线索”；
        （2）被find_best_result调用触发：当find_best_result从终点状态中筛选出最优解（最大资金、最早到达）后，会调用trace_path，传入最优状态的参数，启动回溯过程；
        生成的path_data是write_to_excel的输入：write_to_excel通过读取path_data，将其转化为 Excel 表格，完成结果输出。

13. write_to_excel：结果输出的 “格式化工具”，将路径数据转化为规范表格

        【魔镜魔镜，告诉我，谁是世界上最帅的人？

        当然是屏幕前的同学们呀！！】

        这个方法是整个解题流程的 “收尾环节”—— 将trace_path回溯得到的最优路径数据，按题目要求的格式（包含 0-30 天所有日期、固定列顺序）写入 Excel 文件，同时优化表格显示效果（调整列宽）。它像一个 “数据整理器”，将分散的路径信息（path_data）转化为结构化、易读的表格，既满足题目对输出格式的要求，又方便直观查看每天的状态变化。

核心逻辑：从原始数据到规范表格的全流程处理

方法通过 “补全日期→转换格式→合并数据→优化显示” 的步骤，确保输出的 Excel 表格完整、规范、易读：

（1）创建完整日期框架：确保覆盖所有天数

all_days = pd.DataFrame({\'日期\': range(31)}) # 生成0-30天的完整日期（共31天） 

        这是关键的格式保障：题目要求结果需包含截止日期内的所有天数（0 到 30 天），即使某些天数没有实际状态（如未到达的天数），也需保留日期行。all_days作为 “完整日期模板”，确保后续合并后不会遗漏任何一天。

（2）转换路径数据为 DataFrame：标准化数据格式

path_df = pd.DataFrame(self.path_data) # 将path_data列表转换为pandas数据框 

        self.path_data是trace_path回溯得到的列表（每个元素是一天的状态字典），通过pd.DataFrame转换为结构化数据框，便于后续合并和格式调整（pandas 提供了便捷的表格处理功能）。

（3）合并数据：补全缺失日期

result_df = pd.merge(all_days, path_df, on=\'日期\', how=\'left\') # 左连接保留所有日期 

通过 “左连接”（how=\'left\'）将完整日期框架（all_days）与路径数据（path_df）合并：
        对于path_df中存在的日期（即最优路径经过的天数），保留其状态数据（区域、资金、资源）；
        对于path_df中不存在的日期（即未到达的天数），对应位置显示空值（符合题目 “需包含所有日期” 的要求）。

（4）固定列顺序：符合题目输出要求

result_df = result_df[[\'日期\', \'所在区域\', \'剩余资金数\', \'剩余水量\', \'剩余食物量\']] 

        严格按题目要求的列顺序排列：日期→所在区域→剩余资金数→剩余水量→剩余食物量。这一步确保输出表格的列顺序与题目规范一致，避免因顺序错误导致的格式不符。

（5）写入 Excel 并优化显示：确保内容完整可读

with pd.ExcelWriter(filename, engine=\'openpyxl\') as writer: result_df.to_excel(writer, sheet_name=\'最优路径\', index=False) # 不保留索引列 # 调整列宽：根据内容长度自动适配 worksheet = writer.sheets[\'最优路径\'] for col in worksheet.columns: column = col[0].column_letter # 获取列标识（如A、B、C） max_length = max(len(str(cell.value)) for cell in col) + 2 # 计算最大内容长度（留2字符余量） worksheet.column_dimensions[column].width = max_length 

        写入 Excel 时，指定工作表名称为 “最优路径”，并取消索引列（index=False），确保表格简洁；
        调整列宽是为了避免内容被截断（比如 “剩余资金数” 可能是多位数，列宽不足会显示为 “####”），通过计算每列最大内容长度并增加余量，确保所有数据完整显示。

与其他模块的关联：结果输出的 “最后一公里”

write_to_excel是整个流程的最终输出环节，其数据来源和触发机制明确：
        依赖trace_path生成的path_data：没有回溯得到的路径数据，本方法将无内容可写；
        被find_best_result调用：当find_best_result筛选出最优解并完成路径回溯后，会调用本方法，将结果写入 Excel，完成从 “计算结果” 到 “可提交成果” 的转化。

小结
        write_to_excel的核心价值，是将动态规划得到的抽象路径数据，转化为符合题目规范、易读易用的 Excel 表格。它像一个 “结果包装器”，通过标准化格式、补全缺失信息、优化显示效果，确保解题成果既能满足评分要求，又能清晰展示每天的策略细节（如何时到达矿山、何时在村庄补充资源）。
        没有这个方法，即使找到了最优解，也无法以规范的形式呈现结果 —— 这正是 “解题” 与 “提交成果” 之间不可或缺的桥梁，确保整个解题流程从计算到输出的完整闭环。

14. find_best_result：最优解的 “筛选器”，从终点状态中选出全局最优策略

        【穿成闲散王爷的第三年，我正盘算着傍晚去城南勾栏听新到的那位清倌人唱《雨霖铃》，手里把玩的玉佩还带着体温，就被宫里来的太监连人带座请进了太和殿。​
        殿内烛火明明灭灭，照得百官的脸一半在阴影里。户部尚书正抖着花白胡子念奏疏，说我私通敌国，府中搜出的龙纹锦缎就是铁证。我端着茶盏没应声，眼角余光瞥见御座上的皇帝捻着佛珠，指节泛白。​
        这些日子的诬陷像下饺子似的，今天说我囤兵粮，明天参我通外戚，我都懒得接茬。反正我这王爷当得佛系，除了听曲儿斗蛐蛐，连王府大门都少出，皇帝要猜忌，随他去。​
        可今儿个不一样，那老尚书越说越离谱，竟扯上了先帝的遗诏，话里话外都在说我谋逆。殿内鸦雀无声，所有人的目光都钉在我身上，带着看好戏的冷意。​
        皇帝终于开口，声音轻飘飘的：“七弟，你还有什么话说？”​
        我刚要放下茶盏，脑子里突然炸响一声机械音 ——​
        【叮～检测到宿主正遭受致命诬陷，最强反抗系统已激活！】​
        【新手礼包：言出法随（限定一次）】​
        我愣了愣，随即勾唇笑了。那笑容大概是太突然，站在最前面的几个御史都往后缩了缩。​
        我缓缓起身，玄色王袍扫过冰凉的金砖地，发出细碎的声响。一步步走到殿中，我抬眼看向御座上的人，声音不高不低，却清晰地传遍了整个太和殿：​
        “陛下，臣有一事不明。”​
        皇帝皱眉：“但说无妨。”​
        我微微倾身，眼底的笑意带着三分邪魅 三分漫不经心 四分嘲弄，一字一句问道：​
        “陛下何故谋反？

        这个故事告诉了我们，学习不要看小说，好好听课很重要！！！(*^_^*)】

        这个方法是整个动态规划流程的 “最终裁判”—— 从所有在截止日期前到达终点（区域 27）的状态中，筛选出 “最终资金最高” 且 “到达时间最早” 的最优解。它像一个 “结果分析器”，综合考虑剩余资源的折现价值和到达效率，最终确定符合题目目标的最佳策略，并触发路径回溯和 Excel 导出。

核心逻辑：按 “最终资金 + 到达时间” 双重标准筛选最优解

方法通过 “遍历终点状态→计算最终资金→对比筛选→触发结果处理” 的流程，精准定位最优解：

（1）初始化最优解变量：记录当前最佳状态

best_money = -1 # 初始化为负数，确保任何有效状态都能覆盖 best_day = self.deadline + 1 # 初始化为超期，确保更早到达的状态能覆盖 best_water = 0 best_food = 0 best_state = None # 存储最优状态的资源和前序信息 

        这些变量用于暂存当前找到的最优解：best_money记录最高最终资金，best_day记录最早到达时间，best_state记录对应的资源和前序状态（用于后续回溯）。

（2）遍历所有到达终点的状态：覆盖所有可能的有效路径

# 遍历0到截止日（30天）的所有天数 for day in range(self.deadline + 1): # 检查该天是否有到达终点（区域27）的状态 if self.end in self.dp[day]: # 遍历终点区域的所有状态（水、食物组合） for (water, food), (money, prev_state) in self.dp[day][self.end].items(): 

        这是筛选的基础：只有在截止日期前（day ≤ 30）到达终点的状态才是有效解（题目规则：超期到达失败）。通过遍历所有符合条件的终点状态，确保不遗漏任何潜在的最优解。

（3）计算最终资金：包含剩余资源的折现价值

# 最终资金 = 剩余资金 + 剩余水的退款（基础价的一半） + 剩余食物的退款（基础价的一半） final_money = money + water * self.base_price[\"water\"] / 2 + food * self.base_price[\"food\"] / 2 

        这是关键计算：题目通常隐含 “剩余资源可折现” 的规则（否则剩余资源毫无价值，会导致策略倾向于 “耗尽资源到达终点”，不符合实际逻辑）。这里按基础价格的 50% 计算退款（如每箱水 5 元买，剩余按 2.5 元折现），确保最终资金能反映 “资源剩余” 的实际价值。

（4）双重标准筛选最优解：资金优先，时间次之

# 条件1：最终资金更高 → 更新最优解 # 条件2：资金相同但到达时间更早 → 更新最优解 if (final_money > best_money or (final_money == best_money and day < best_day)): best_money = final_money best_day = day best_water = water best_food = food best_state = (water, food, prev_state) # 记录资源和前序状态，用于回溯 

这是筛选的核心逻辑，完全贴合题目目标：
        首要目标是 “最大化最终资金”（final_money > best_money）；
        次要目标是 “相同资金下，最早到达更优”（day < best_day），因为更早到达意味着策略更高效（或有冗余时间应对突发情况）。

（5）处理最优解：回溯路径并导出结果

if best_state: # 若找到有效最优解 # 回溯路径：从终点倒推至起点，收集每天数据 self.trace_path(best_day, self.end, best_state[0], best_state[1], best_state[2]) # 写入Excel：将路径数据格式化为表格 self.write_to_excel() 

        找到最优解后，通过trace_path还原完整路径，再通过write_to_excel输出结果，完成从 “计算最优解” 到 “展示最优策略” 的闭环。

与其他模块的关联：结果输出的 “总开关”

        find_best_result是整个程序的 “结果出口”，串联了动态规划的最终计算与结果展示：
        （1）依赖dp容器中存储的终点状态：所有到达终点的状态都来自之前的process_day迭代，是动态规划的最终产物；
        （2）调用trace_path触发路径回溯：将分散的状态关联成完整路径；
        （3）调用write_to_excel完成结果输出：将路径数据转化为规范表格。
        如果没有这个方法，动态规划计算出的海量状态将无法转化为 “最优解”，整个程序只能生成数据，无法得出结论。

为什么要遍历所有到达终点的状态？

        动态规划可能生成多条到达终点的路径（不同天数、不同资源组合），每条路径的最终资金可能不同：
        例如，第 25 天到达终点，剩余资源多但资金少；第 30 天到达终点，资源少但资金多 —— 需要计算最终资金（含折现）才能判断优劣；
        若只检查最后一天（第 30 天）的状态，可能错过更早到达且资金更高的解（如第 28 天到达的解可能更优）。
        遍历所有天数的终点状态，确保了全局最优解不会被遗漏。

小结
        find_best_result的核心价值，是从动态规划生成的所有有效终点状态中，通过 “最终资金 + 到达时间” 的双重标准，筛选出全局最优解，并触发路径回溯和结果输出。它像一个 “解题终点站”，将前面所有模块的计算成果（dp状态）转化为明确的最优策略和可展示的结果，完成整个解题流程的闭环。
        没有这个方法，动态规划的迭代计算就失去了 “目标”—— 无法确定哪个状态是最优解，更无法输出符合题目要求的结果，整个程序的价值也就无法体现。

15. solve：问题求解的 “总指挥”，统筹全流程的主函数

        【同学们好好听课！仔细观察题目，流程二字，emmm，可以想到什么呢？

        没错！流程里面有个流字，很容易就可以联想到蜡笔小新里面的流水面，进而可以想到蜡笔小新里面吃年糕的那一集！

        啊？你问我这和这个函数有什么关系？

        当然有啊，因为写着写着主播有点想吃青菜年糕了

        咳咳，回归正题】

        这个方法是整个解题逻辑的 “总入口”—— 通过按顺序调用初始化、每日迭代、结果筛选等核心方法，统筹从 “起点状态” 到 “最优解输出” 的完整流程。它像一个 “流程控制器”，确保动态规划的各个环节按正确顺序执行，最终高效地输出问题的最优解。

核心逻辑：按 “初始化→迭代处理→结果筛选” 的流程推进

方法通过三个关键步骤，实现从 “准备” 到 “计算” 再到 “输出” 的闭环：

（1）初始化第 0 天状态：搭建动态规划的起点

print(\"初始化第0天状态...\") self.initialize_dp() # 调用initialize_dp生成第0天的所有初始状态 

        这是流程的第一步：通过initialize_dp生成第 0 天在起点区域（区域 1）的所有合法资源组合（水、食物、资金），为后续的每日迭代提供 “初始燃料”。打印提示信息是为了让用户了解程序当前进度（避免长时间无输出导致的困惑）。

（2）迭代处理每一天：推动动态规划的状态流转

# 遍历从第0天到第29天（共30天），生成第1天到第30天的状态 for day in range(self.deadline): self.process_day(day) # 调用process_day处理当天，生成次日状态 

        这是流程的核心：通过循环调用process_day，按时间顺序（第 0 天→第 1 天→…→第 29 天）处理每一天的状态，生成下一天的状态。30 次循环后，dp容器中将包含从第 0 天到第 30 天的所有有效状态，覆盖所有可能的路径和策略。

（3）筛选最优结果：输出最终答案

print(\"寻找最优结果...\") self.best_result = self.find_best_result() # 调用find_best_result筛选最优解 return self.best_result # 返回最优解信息 

        这是流程的终点：通过find_best_result从所有到达终点的状态中，筛选出 “最终资金最高且到达时间最早” 的最优解，并触发路径回溯（trace_path）和 Excel 导出（write_to_excel）。最终返回最优解的关键信息（到达时间、剩余资源、最终资金），完成整个解题流程。

与其他模块的关联：全流程的 “串联者”

        solve方法是所有核心模块的 “粘合剂”，其执行顺序直接决定了整个程序的正确性：
        （1）必须先调用initialize_dp，否则dp容器为空，后续process_day无初始状态可处理；
        （2）必须按顺序循环调用process_day(day)（从 0 到 29），因为第day+1天的状态依赖第day天的状态，逆序或跳跃会导致状态缺失；
        （3）必须最后调用find_best_result，因为此时dp容器已包含所有天数的状态，才能确保筛选出的是全局最优解。

为什么需要这样的流程设计？

        动态规划的本质是 “按时间顺序逐步构建最优解”，solve的流程设计完全遵循这一原则：
        （1）初始化：建立起点状态，确保有 “初始解”；
        （2）迭代：按天推进，基于前一天的解生成当天的解，符合 “最优子结构”（当天的最优解依赖前一天的最优解）；
        （3）筛选：在所有可能的解中选择全局最优，完成 “从局部最优到全局最优” 的跃迁。
        这种流程既保证了计算的完整性（覆盖所有可能路径），又确保了效率（通过update_next_state筛选冗余状态）。

小结
        solve的核心价值，是作为整个解题流程的 “总指挥”—— 通过严格的顺序控制，将初始化、每日迭代、结果筛选等独立模块串联成一个完整的动态规划解题链。它不需要关注具体的状态计算细节，只需确保每个环节在正确的时间被调用，最终高效地输出符合题目要求的最优解。
        没有这个 “统筹者”，各个模块将是零散的 “零件”，无法协同工作生成最终结果 —— 这正是 “整体大于部分之和” 在程序设计中的体现。

        【哇塞，你居然认认真真的看完了，太厉害了吧！

        某读者内心：结束了么，不过如此，看来是时候轮到我大展身手了(′д｀ )…彡…彡

        咳咳，主播提醒这位同学先别着急，到现在为止我们完成了整个类以及方法的实现，但是我们还没有创建实例调用呢，这就像某天你肚子痛飞速回家，打开卫生间的门，做好万全的准备，还特地检查了卫生间有没有纸，坐在马桶上一泻千里，嗯~舒服，就是这个感？？不对，你只是坐下了，但是你还没脱裤子呢，同学！】

16.言归正传，来吧，展示：

（1）设置中文显示：避免乱码问题

pd.set_option(\'display.unicode.east_asian_width\', True) 

        这是针对 pandas 的显示设置：确保在输出中文（如 “剩余资金数”“所在区域”）时不会出现乱码或对齐问题，为后续的结果展示和 Excel 导出提供基础支持。

（2）创建实例并启动求解

game = DesertCrossing() # 创建沙漠穿越问题的实例 result = game.solve() # 调用solve方法启动解题流程 

        DesertCrossing()：实例化整个问题的处理类，初始化所有参数（如天气序列、地图、资源价格等）；
        game.solve()：调用之前分析的主函数solve，启动动态规划的全流程（初始化→每日迭代→筛选最优解），最终返回最优解的核心信息（到达时间、剩余资源、最终资金）。

（3）展示最优解结果

print(\"\\n第一关最优解：\") for key, value in result.items(): print(f\"{key}：{value}\") 

        将solve返回的最优解字典（result）格式化输出，用清晰的键值对展示核心结果（如 “到达时间：25 天”“最终资金：15000 元”），让用户能快速了解解题结论。

与其他模块的关联：程序运行的 “总启动器”

        这部分代码是所有逻辑的 “触发点”：
        （1）它创建DesertCrossing实例，间接初始化了所有内部参数（如weather、graph、dp等）；
        （2）它调用solve()方法，串联了initialize_dp、process_day、find_best_result等核心方法，启动了整个动态规划流程；
        最终的结果输出依赖find_best_result返回的result字典，是解题流程的 “终端展示”。

小结
        这部分入口代码的核心价值，是为整个程序提供 “一键启动” 的能力 —— 用户只需运行脚本，就能自动完成从参数初始化、动态规划计算到结果展示的全流程。它像一个 “程序遥控器”，隐藏了复杂的内部逻辑，只向用户暴露简单的启动操作和清晰的结果输出，是连接程序开发者与使用者的 “桥梁”。
        没有这个入口，用户需要手动调用DesertCrossing的多个方法（如先初始化、再循环调用process_day、最后调用find_best_result），大大增加了使用难度，降低了程序的易用性。

五、第一关完整代码 1.0

        前面我们拆解了各核心函数的逻辑，现在给出可直接运行的完整代码

        【嗯？这位同学，谁允许你考试知识点不复习，直接过来看期末试卷的！！！】

from collections import defaultdictimport pandas as pd # 导入pandas用于处理表格class DesertCrossing: def __init__(self): # 初始化游戏参数 self.init_parameters() # 动态规划状态存储：dp[t][u] = { (w, f): (max_money, prev_state) } self.dp = [defaultdict(dict) for _ in range(self.deadline + 1)] # 记录最优结果和路径数据 self.best_result = None self.path_data = [] # 存储路径数据的列表 def init_parameters(self): \"\"\"初始化游戏基本参数\"\"\" self.max_weight = 1200 # 最大负重(千克) self.deadline = 30 # 截止日期(天) self.initial_money = 10000 # 初始资金 self.base_income = 1000 # 挖矿基础收益 # 每箱重量(千克) self.box_weight = {\"water\": 3, \"food\": 2} # 不同天气条件下的基础消耗量(箱) self.weather_consumption = { \"晴朗\": {\"water\": 5, \"food\": 7}, \"高温\": {\"water\": 8, \"food\": 6}, \"沙暴\": {\"water\": 10, \"food\": 10} } # 价格设置 self.base_price = {\"water\": 5, \"food\": 10} self.village_price = {\"water\": 10, \"food\": 20} # 村庄价格是基准价格的2倍 # 地图: 区域连接关系 self.graph = { 1: [2, 25],  # 起点 2: [1, 3],  3: [2, 4, 25], 4: [3, 5, 24, 25], 5: [4, 6, 24], 6: [5, 7, 23, 24], 7: [6, 8, 22], 8: [7, 9, 22], 9: [8, 10, 15, 16, 17, 21, 22], 10: [9, 11, 13, 15], 11: [10, 12, 13], 12: [11, 13, 14],  # 矿山 13: [10, 11, 12, 14, 15],  14: [12, 13, 15, 16],15: [9, 10, 13, 14, 16], # 村庄 16: [9, 14, 15, 17, 18],  17: [9, 16, 18, 21], 18: [16, 17, 19, 20],19: [18, 20], 20: [18, 19, 21], 21: [9, 17, 20, 22, 23, 27],  22: [7, 8, 9, 21, 23],  23: [6, 21, 22, 24, 26],  24: [4, 5, 6, 23, 25, 26],  25: [1, 3, 4, 24, 26],  26: [23, 24, 25, 27],27: [] # 终点(无出边) } self.start = 1 # 起点 self.end = 27 # 终点 self.mines = {12} # 矿山区域 self.villages = {15} # 村庄区域 # 30天的天气序列（索引0-29对应第0天到第29天） self.weather = [ \"高温\", \"高温\", \"晴朗\", \"沙暴\", \"晴朗\", \"高温\", \"沙暴\", \"晴朗\", \"高温\", \"高温\", \"沙暴\", \"高温\", \"晴朗\", \"高温\", \"高温\", \"高温\", \"沙暴\", \"沙暴\", \"高温\", \"高温\", \"晴朗\", \"晴朗\", \"高温\", \"晴朗\", \"沙暴\", \"高温\", \"晴朗\", \"晴朗\", \"高温\", \"高温\" ] def is_valid_weight(self, water, food): \"\"\"检查负重是否在允许范围内\"\"\" total_weight = water * self.box_weight[\"water\"] + food * self.box_weight[\"food\"] return total_weight <= self.max_weight def get_base_consumption(self, day): \"\"\"获取某天的基础消耗量（确保day在有效范围内）\"\"\" if day = len(self.weather): raise IndexError(f\"天气索引超出范围: day={day}, 有效范围0-{len(self.weather)-1}\") weather = self.weather[day] return self.weather_consumption[weather] def initialize_dp(self): \"\"\"初始化第0天的状态(起点购买资源)\"\"\" start_area = self.start # 优化初始购买量的遍历范围 max_water = min( self.initial_money // self.base_price[\"water\"], self.max_weight // self.box_weight[\"water\"] ) for water in range(0, max_water + 1): remaining_money = self.initial_money - water * self.base_price[\"water\"] if remaining_money  self.initial_money:  continue money = self.initial_money - cost state = (water, food) # 只保留该状态下的最大资金 if state not in self.dp[0][start_area] or money > self.dp[0][start_area][state][0]:  self.dp[0][start_area][state] = (money, None) # 初始状态没有前序 def process_day(self, day): \"\"\"处理第day天的状态，计算第day+1天的状态\"\"\" if day >= self.deadline: return current_weather = self.weather[day] if day % 5 == 0: # 每5天打印一次进度 print(f\"处理第 {day} 天，天气: {current_weather}\") # 遍历当前天的所有区域 for area in list(self.dp[day].keys()): # 遍历该区域的所有状态 for (water, food), (money, prev_state) in list(self.dp[day][area].items()): # 如果已经到达终点，不需要继续处理 if area == self.end:  continue # 根据天气和区域，生成可能的行动 possible_actions = self.get_possible_actions(area, current_weather, day) # 处理每种可能的行动 for action in possible_actions:  self.process_action(day, area, water, food, money, prev_state, action) def get_possible_actions(self, area, weather, day): \"\"\"根据当前状态获取可能的行动\"\"\" actions = [] # 沙暴日只能停留 if weather == \"沙暴\": # 矿山特殊处理 if area in self.mines: # 判断是否是当天到达矿山（前一天不在此区域） is_new_arrival = self.is_new_arrival(day, area) if is_new_arrival:  actions.append(\"stay\") # 到达矿山当天只能普通停留 else:  actions.append(\"stay\") # 普通停留  actions.append(\"mine\") # 挖矿 else: actions.append(\"stay\") # 普通区域停留 else: # 非沙暴日可以移动或停留 # 添加移动到相邻区域的行动 for neighbor in self.graph[area]: actions.append(f\"move_{neighbor}\") # 添加停留行动 if area in self.mines: # 判断是否是当天到达矿山 is_new_arrival = self.is_new_arrival(day, area) if is_new_arrival:  actions.append(\"stay\") # 到达矿山当天只能普通停留 else:  actions.append(\"stay\") # 普通停留  actions.append(\"mine\") # 挖矿 else: actions.append(\"stay\") # 普通区域停留 return actions def is_new_arrival(self, day, area): \"\"\"判断是否是当天到达该区域（前一天不在此区域）\"\"\" if day == 0: return area == self.start # 第0天只有起点是初始位置 # 检查前一天是否在该区域有任何状态 return len(self.dp[day-1].get(area, {})) == 0 def process_action(self, day, area, water, food, money, prev_state, action): \"\"\"处理具体行动，更新下一天的状态\"\"\" next_day = day + 1 if next_day > self.deadline: return  current_weather = self.weather[day] base_consumption = self.get_base_consumption(day) # 计算资源消耗和下一区域 if action.startswith(\"move\"): # 移动到相邻区域，消耗2倍基础资源 next_area = int(action.split(\"_\")[1]) water_cost = 2 * base_consumption[\"water\"] food_cost = 2 * base_consumption[\"food\"] new_money = money elif action == \"stay\": # 普通停留，消耗基础资源 next_area = area water_cost = base_consumption[\"water\"] food_cost = base_consumption[\"food\"] new_money = money elif action == \"mine\": # 挖矿，消耗3倍基础资源，获得收益 next_area = area water_cost = 3 * base_consumption[\"water\"] food_cost = 3 * base_consumption[\"food\"] new_money = money + self.base_income # 挖矿收益 else: return # 检查资源是否足够 new_water = water - water_cost new_food = food - food_cost if new_water < 0 or new_food  0 and max_buy_water > 0: buy_water = min(needed_water, max_buy_water) new_m = money - buy_water * self.village_price[\"water\"] self.update_next_state(next_day, next_area, water + buy_water, food, new_m, prev_day, prev_area, prev_water, prev_food, action + \"_buy_water\") # 策略3：只购买食物（如果需要） if needed_food > 0: max_buy_food = min( needed_food, money // self.village_price[\"food\"], (self.max_weight - water * self.box_weight[\"water\"]) // self.box_weight[\"food\"] - food ) if max_buy_food > 0: buy_food = min(needed_food, max_buy_food) new_m = money - buy_food * self.village_price[\"food\"] self.update_next_state(next_day, next_area, water, food + buy_food, new_m, prev_day, prev_area, prev_water, prev_food, action + \"_buy_food\") # 策略4：同时购买水和食物（如果需要） if needed_water > 0 and needed_food > 0 and max_buy_water > 0: remaining_money_after_water = money - max_buy_water * self.village_price[\"water\"] if remaining_money_after_water > 0: max_buy_food = min(  needed_food,  remaining_money_after_water // self.village_price[\"food\"],  (self.max_weight - (water + max_buy_water) * self.box_weight[\"water\"]) // self.box_weight[\"food\"] - food ) if max_buy_food > 0:  new_m = remaining_money_after_water - max_buy_food * self.village_price[\"food\"]  self.update_next_state(next_day, next_area, water + max_buy_water, food + max_buy_food, new_m,  prev_day, prev_area, prev_water, prev_food, action + \"_buy_both\") def update_next_state(self, next_day, next_area, water, food, money, prev_day, prev_area, prev_water, prev_food, action): \"\"\"更新下一天的状态，保留最大资金\"\"\" if not self.is_valid_weight(water, food): return  state = (water, food) # 记录前序状态，用于回溯路径 previous_state = (prev_day, prev_area, prev_water, prev_food, action) # 只保留该状态下的最大资金 if state not in self.dp[next_day][next_area]: self.dp[next_day][next_area][state] = (money, previous_state) else: current_max_money = self.dp[next_day][next_area][state][0] if money > current_max_money: self.dp[next_day][next_area][state] = (money, previous_state) def trace_path(self, day, area, water, food, prev_state): \"\"\"回溯最优路径，收集数据用于Excel导出\"\"\" # 获取当前状态的资金 current_money = self.dp[day][area].get((water, food), [0, None])[0] # 避免重复记录同一日期 if not any(item[\'日期\'] == day for item in self.path_data): self.path_data.append({ \'日期\': day, \'所在区域\': area, \'剩余资金数\': current_money, \'剩余水量\': water, \'剩余食物量\': food }) if prev_state and day > 0: prev_day, prev_area, prev_water, prev_food, action = prev_state prev_state_data = self.dp[prev_day][prev_area].get((prev_water, prev_food), [0, None]) self.trace_path(prev_day, prev_area, prev_water, prev_food, prev_state_data[1]) def write_to_excel(self, filename=\"最优路径.xlsx\"): \"\"\"使用pandas将路径数据写入Excel，生成指定格式表格\"\"\" # 1. 创建包含0-30天的完整日期框架 all_days = pd.DataFrame({\'日期\': range(31)}) # 2. 将路径数据转换为DataFrame path_df = pd.DataFrame(self.path_data) # 3. 合并数据，确保所有日期都存在 result_df = pd.merge(all_days, path_df, on=\'日期\', how=\'left\') # 4. 确保列顺序正确 result_df = result_df[[\'日期\', \'所在区域\', \'剩余资金数\', \'剩余水量\', \'剩余食物量\']] # 5. 写入Excel with pd.ExcelWriter(filename, engine=\'openpyxl\') as writer: result_df.to_excel(writer, sheet_name=\'最优路径\', index=False) # 6. 调整列宽优化显示 worksheet = writer.sheets[\'最优路径\'] for col in worksheet.columns: column = col[0].column_letter # 获取列字母（如A、B、C） # 计算该列最大内容长度 max_length = max(len(str(cell.value)) for cell in col) + 2 worksheet.column_dimensions[column].width = max_length print(f\"\\n最优路径已写入Excel文件：{filename}\") def find_best_result(self): \"\"\"找到到达终点的最优结果\"\"\" best_money = -1 best_day = self.deadline + 1 best_water = 0 best_food = 0 best_state = None # 检查所有在截止日期前到达终点的状态 for day in range(self.deadline + 1): if self.end in self.dp[day]: for (water, food), (money, prev_state) in self.dp[day][self.end].items():  # 计算最终资金（加上剩余资源退款）  final_money = money + water * self.base_price[\"water\"] / 2 + food * self.base_price[\"food\"] / 2  # 更新最优解  if (final_money > best_money or (final_money == best_money and day < best_day)): best_money = final_money best_day = day best_water = water best_food = food best_state = (water, food, prev_state) # 回溯最优路径并写入Excel if best_state: self.trace_path(best_day, self.end, best_state[0], best_state[1], best_state[2]) self.write_to_excel() return { \"到达时间\": best_day, \"剩余水\": best_water, \"剩余食物\": best_food, \"最终资金\": round(best_money) } def solve(self): \"\"\"求解问题的主函数\"\"\" # 初始化第0天状态 print(\"初始化第0天状态...\") self.initialize_dp() # 处理每一天 for day in range(self.deadline): self.process_day(day) # 找到最优结果 print(\"寻找最优结果...\") self.best_result = self.find_best_result() return self.best_resultif __name__ == \"__main__\": # 确保中文正常显示 pd.set_option(\'display.unicode.east_asian_width\', True) # 创建游戏实例并求解 game = DesertCrossing() result = game.solve() # 输出结果 print(\"\\n第一关最优解：\") for key, value in result.items(): print(f\"{key}：{value}\")

结果如图：

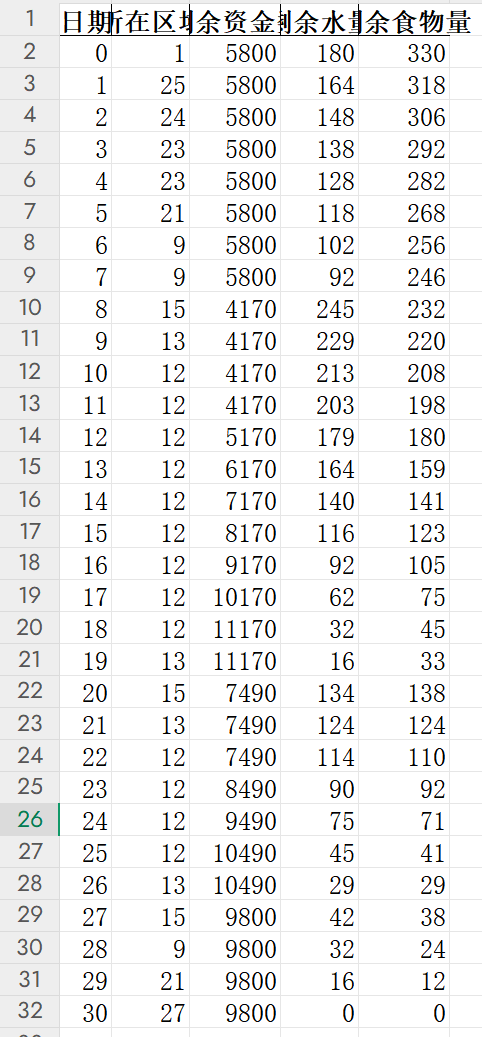
但是这样子真的完整了吗？

没错！问的就是你呢！这位同学，仔细观察观察。

六、截止日期对结果的影响 —— 为什么需要多场景对比？

        截止到上文结束，聪明的同学可能已经发现了问题：主播主播，图片上面第20天已经11170元了，怎么不直接回到终点，还有去村庄买物资继续挖矿。

        主播表示：既然题目都截止到第30天了，那我们假装看不见，照做就好了呗【不是】

        这就是要进行多场景对比的原因。实际解题中，“固定截止日期的最优解”≠“全局最优解”。截止日期作为核心约束，直接决定了策略的可行性 —— 比如同样是 30 天，对 “能挖矿” 和 “不能挖矿” 的场景来说，最优解可能天差地别。这正是需要多场景对比的关键原因。

一、截止日期如何 “改写” 最优策略？

第一关的 30 天是 “最大截止期”，但不同子场景的 “有效截止期” 差异极大，策略会因此完全不同：
1. 短期截止（如≤X 天，X 为纯赶路最短时间）
此时时间仅够从起点直奔终点，根本没时间绕道矿山【所以，有时候就是要大胆出手！】
        最优策略：纯赶路，优先选择最短路径，初始购买资源刚好满足消耗（避免多买浪费资金）。
        例：若纯赶路最短需 15 天，那么 15 天截止期的最优解一定是 “不挖矿，按最短路径狂奔”，任何涉及挖矿的策略都会因超时失败。
2. 中期截止（如 X＜截止期＜Y，Y 为挖矿必要时间）
时间比纯赶路多，但仍不够完成 “到矿山 + 挖矿 + 到终点” 全流程（比如需要 20 天，但截止期只有 18 天）【赚钱还是很重要的！】
        最优策略：仍以赶路为主，但可适当绕路经过村庄补充资源，避免因资源不足中途失败。
        此时若强行挖矿，会因 “到终点时间超期” 导致前功尽弃，反而不如纯赶路收益高。
3. 长期截止（如≥Y 天，Y 为挖矿必要时间）
时间足够支撑挖矿流程，此时需权衡 “挖矿收益” 与 “额外消耗”：【不要一直舔啊，混蛋！】
        若挖矿 1 天的收益（1000 元）＞挖矿多消耗的资源成本（如多买水和食物花 800 元），则挖矿更优；
        若资源成本过高（如沙暴日挖矿消耗太大），则可能 “不挖矿反而赚更多”。

二、只算固定截止期，可能错过全局最优解

举个具体例子：
        30 天截止期下，最优解是 “挖矿3天，回村庄补给，再接着挖矿2天，最后再前往终点，最终资金 15000 元”；
        但 25 天截止期时，可能会由于时间刚好够挖矿 3 天后，直接前往终点，最终资金反而能达到 16000 元（少挖几天节省了挖矿成本和往返村庄买物资的成本）；

        【理解不了？那我换个说法！

        教学楼的走廊还是老样子，墙皮掉了几块，阳光斜斜切进来，在地上投出粉笔灰的轨迹。刚跟班主任聊完天，手里还捏着她塞的橘子糖，糖纸窸窣响着，像极了高中时藏在袖口的心跳。
        路过三楼最东头的教室时，脚步忽然顿住。
        靠窗的位置坐着个男孩，笔尖在练习册上沙沙动，侧脸绷得紧，像是在跟一道数学题死磕。他左手搭在额头上，指节抵着眉骨，姿势熟得让我喉咙发紧 —— 那是我当年的姿势。
        走廊里有脚步声过来，一个穿校服的女生抱着作业本走过，发尾扫过男孩的桌角时，她顿了顿。
        男孩没抬头，可我看见他搭在额头上的手指几不可察地蜷了蜷。
        女生忽然笑了，很浅的笑意，像初春刚融的冰棱，顺着嘴角漫到眼睛里。她没说话，轻轻踮了踮脚，把一本掉在地上的练习册捡起来，放在男孩桌沿，然后继续往前走。
        直到她的影子消失在走廊尽头，男孩才慢慢放下手，指尖在刚才女生碰过的地方蹭了蹭，耳尖红得像被阳光烤过的樱桃。
        我站在原地，橘子糖在嘴里化出酸甜的味。
        想起高三最后那节自习课，她也是这样抱着作业本从旁边过，发绳上的小铃铛叮铃响。我盯着摊开的数学卷，其实一道题也没看进去，只听见自己的呼吸撞在胸腔里，闷闷的。她走过去很远了，我才敢抬头，看见她的背影拐进办公室，发尾的铃铛还在风里荡。
        那时总想着，等考完试，等再优秀一点，等攒够了勇气。可试卷收上去那天，人潮涌着散场，我攥着写了半页的纸条，终究没敢递出去。后来同学录上她的字迹娟秀，只留了一句 “前程似锦”，再没别的。
        风从走廊穿过去，带着操场的青草味。教室里的男孩低头继续做题，可嘴角的弧度没压下去，像藏了颗没说出口的糖。
        我笑了笑，转身往下走。橘子糖的甜味漫到舌尖，原来有些没说出口的话，没走完的路，总会有人替你，轻轻续上。

        我是想说，有时候兜兜转转一辈子可能都不如最初的勇敢】

        所以，如果只算 30 天，有时候就会错过这个 “时间更短但收益更高” 的全局最优解。

这就是多场景对比的核心价值：截止日期本身会改变策略的成本收益比，只有遍历有效范围，才能找到 “在所有可能时间限制下，真正收益最高” 的方案。

三、代码如何高效实现多场景对比？

        【好了，回到课堂。】

        新增函数的核心目标很明确：缩小有效计算范围，精准定位值得对比的截止日期，避免盲目遍历 30 天的所有可能，从而提升效率。
        具体来说，这里有两个关键的约束逻辑：
        （1）截止日期不能小于 “起点到终点的最短直接时间”。因为如果截止日期短于这个时间，连最直接的路径都无法走完，更别说抵达终点了 —— 这类无效的截止日期显然没必要纳入对比。
        （2）截止日期与 “挖矿所需的最小时间” 直接相关。整个穿越过程中，我们主要消耗预先购买的物资，而挖矿是唯一能增加最终资金的方式。因此：
        如果截止日期短于 “挖矿所需的最小时间”（即连 “到达矿山→停留 1 天→挖矿 1 天→前往终点” 这个基础流程都无法完成），那么最优策略必然是 “不挖矿，直接从起点到终点”，此时无需对比更多方案；
        如果截止日期大于等于 “挖矿所需的最小时间”，情况就会变得复杂：不同的截止日期会影响物资购买策略（比如是否在村庄多储备资源）、挖矿天数（比如多挖 1 天还是提前出发），进而直接影响最终资金 —— 这类截止日期才是值得重点对比的对象。
        通过这样的逻辑筛选，代码就能跳过无效的截止日期，只聚焦于真正能产生策略差异的范围，从而高效实现多场景对比。而要计算时间的差异，我们可以采用bfs来计算两个地区之间的最短路径。

1. BFS 最短路径计算（calculate_shortest_path）
        作用：快速找到 “起点→终点”“起点→矿山”“矿山→终点” 的最少天数，为判断策略可行性提供依据。

def calculate_shortest_path(graph, start, end): \"\"\"用BFS计算两点间最短路径（步数）\"\"\" if start == end: return 0 visited = {start: 0} # 记录到达每个节点的最少步数 queue = deque([start]) while queue: current = queue.popleft() for neighbor in graph[current]:  if neighbor not in visited:  visited[neighbor] = visited[current] + 1  queue.append(neighbor)  if neighbor == end:return visited[neighbor] # 找到终点即返回 return float(\'inf\') # 无法到达 

关键价值：

（1）直接得到 “纯赶路最短时间”（记为min_direct_days），截止日期＜该值时，无解；
（2）计算 “起点→矿山”“矿山→终点” 的最短时间，为判断挖矿可行性提供基础。

2. 挖矿必要时间计算（calculate_min_mine_days）
        作用：计算 “执行挖矿策略的最少时间”（需满足 “到矿山 + 1天停留 + 1天挖矿 + 到终点”）。

def calculate_min_mine_days(graph, start, end, mines): \"\"\"计算多矿区场景下的挖矿最少必要时间（取最小值）\"\"\" min_days = float(\'inf\') for mine in mines: M = calculate_shortest_path(graph, start, mine) # 到矿山的最短时间 E = calculate_shortest_path(graph, mine, end) # 矿山到终点的最短时间 mine_min_days = M + 2 + E # 2天=1天停留（不能挖矿）+1天挖矿 if mine_min_days < min_days:  min_days = mine_min_days return min_days 

关键价值：

（1）得到 “挖矿策略的最低时间要求”（记为min_mine_days）；
（2）截止日期≥该值时，才需要考虑挖矿策略，否则直接排除。

用 BFS 算阈值：
        shortest_direct（纯赶路最短时间）：低于此值的截止期直接排除（不可能完成任务）；
        min_mine_days（挖矿最少必要时间）：低于此值的截止期无需考虑挖矿策略。
分阶段对比：
        短期（≤min_mine_days）：只算纯赶路；（只需要计算短期最短的一天即可，因为短期到长期的这段时间无法挖矿，也就无法产生收益，赶路多了只会降低最终资金）
        长期（≥min_mine_days）：对比挖矿与不挖矿的收益。

 这种方式既能覆盖所有可能产生最优解的场景，又能减少无效计算（比如不用测试 10 天这种明显不可能完成的截止期），避免了 “盲目遍历所有 30 天”，精准锁定有效范围。

        至此，我们就完成了第一关的解答。

        【有的同学可能会问了：主播主播，这也太吃操作了吧，有没有什么更简单的方法！】

        【主播表示：有的兄弟，有的，这样子的方法一共有九种，分别是...

           咳咳，主播现在要介绍的是高中让人最最闻风丧胆的三个字：注意到！！！

           先前眼尖的兄弟发现了在第20天左右，资金达到了最大值，此时直接去终点是不是收益最高呢？那我们可以直接看地图，从矿山到终点最快是12->24>15>9>21->27，一共五天，那我们就可以把截止日期改成第25天，然后在这附近来回尝试即可，效率快，精准打击，直切要害！】

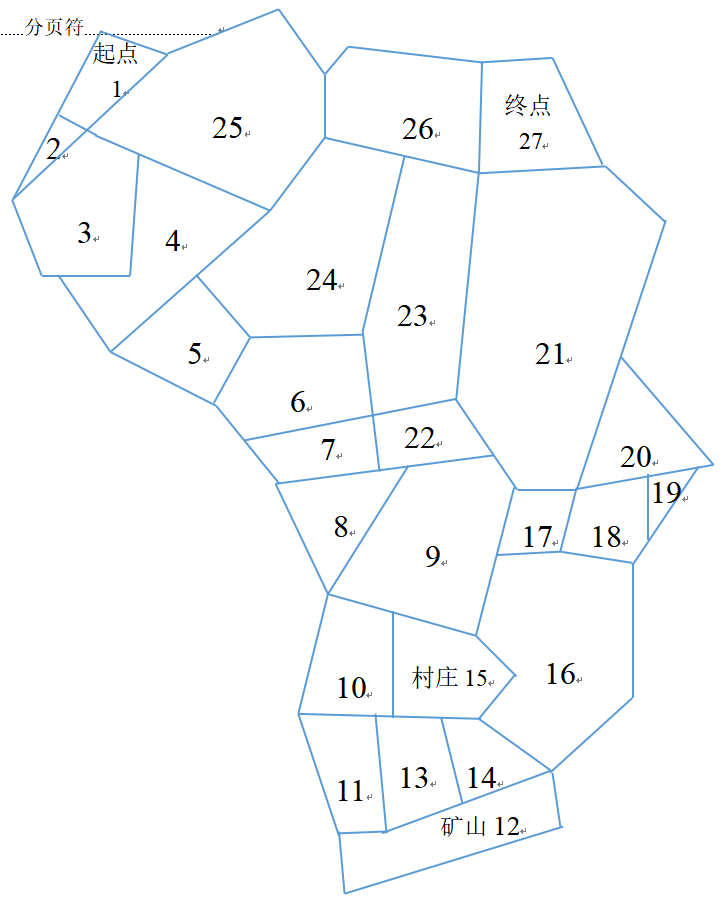
七、第一关完整代码 2.0

        【成就感满满呀！】

from collections import defaultdict, dequeimport pandas as pdclass DesertCrossing: def __init__(self, deadline): self.deadline = deadline # 动态接收截止日期 self.init_parameters() # 动态规划状态存储：dp[t][u] = { (w, f): (max_money, prev_state) } self.dp = [defaultdict(dict) for _ in range(self.deadline + 1)] # 记录最优结果和路径数据 self.best_result = None self.path_data = [] # 存储路径数据的列表 def init_parameters(self): \"\"\"初始化游戏基本参数（第一关设置）\"\"\" self.max_weight = 1200 # 最大负重(千克) self.initial_money = 10000 # 初始资金 self.base_income = 1000 # 挖矿基础收益 # 每箱重量(千克) self.box_weight = {\"water\": 3, \"food\": 2} # 不同天气条件下的基础消耗量(箱) self.weather_consumption = { \"晴朗\": {\"water\": 5, \"food\": 7}, \"高温\": {\"water\": 8, \"food\": 6}, \"沙暴\": {\"water\": 10, \"food\": 10} } # 价格设置 self.base_price = {\"water\": 5, \"food\": 10} self.village_price = {\"water\": 10, \"food\": 20} # 村庄价格是基准价格的2倍 # 第一关地图: 区域连接关系 self.graph = { 1: [2, 25],  # 起点 2: [1, 3],  3: [2, 4, 25], 4: [3, 5, 24, 25], 5: [4, 6, 24], 6: [5, 7, 23, 24], 7: [6, 8, 22], 8: [7, 9, 22], 9: [8, 10, 15, 16, 17, 21, 22], 10: [9, 11, 13, 15], 11: [10, 12, 13], 12: [11, 13, 14],  # 矿山 13: [10, 11, 12, 14, 15],  14: [12, 13, 15, 16],15: [9, 10, 13, 14, 16], # 村庄 16: [9, 14, 15, 17, 18],  17: [9, 16, 18, 21], 18: [16, 17, 19, 20],19: [18, 20], 20: [18, 19, 21], 21: [9, 17, 20, 22, 23, 27],  22: [7, 8, 9, 21, 23],  23: [6, 21, 22, 24, 26],  24: [4, 5, 6, 23, 25, 26],  25: [1, 3, 4, 24, 26],  26: [23, 24, 25, 27],27: [] # 终点(无出边) } self.start = 1 # 起点 self.end = 27 # 终点 self.mines = {12} # 矿山区域 self.villages = {15} # 村庄区域 # 30天的天气序列（索引0-29对应第0天到第29天） self.weather = [ \"高温\", \"高温\", \"晴朗\", \"沙暴\", \"晴朗\", \"高温\", \"沙暴\", \"晴朗\", \"高温\", \"高温\", \"沙暴\", \"高温\", \"晴朗\", \"高温\", \"高温\", \"高温\", \"沙暴\", \"沙暴\", \"高温\", \"高温\", \"晴朗\", \"晴朗\", \"高温\", \"晴朗\", \"沙暴\", \"高温\", \"晴朗\", \"晴朗\", \"高温\", \"高温\" ] def is_valid_weight(self, water, food): \"\"\"检查负重是否在允许范围内\"\"\" total_weight = water * self.box_weight[\"water\"] + food * self.box_weight[\"food\"] return total_weight <= self.max_weight def get_base_consumption(self, day): \"\"\"获取某天的基础消耗量（确保day在有效范围内）\"\"\" if day = len(self.weather): raise IndexError(f\"天气索引超出范围: day={day}, 有效范围0-{len(self.weather)-1}\") weather = self.weather[day] return self.weather_consumption[weather] def initialize_dp(self): \"\"\"初始化第0天的状态(起点购买资源)\"\"\" start_area = self.start # 优化初始购买量的遍历范围 max_water = min( self.initial_money // self.base_price[\"water\"], self.max_weight // self.box_weight[\"water\"] ) for water in range(0, max_water + 1): remaining_money = self.initial_money - water * self.base_price[\"water\"] if remaining_money  self.initial_money:  continue money = self.initial_money - cost state = (water, food) # 只保留该状态下的最大资金 if state not in self.dp[0][start_area] or money > self.dp[0][start_area][state][0]:  self.dp[0][start_area][state] = (money, None) # 初始状态没有前序 def process_day(self, day): \"\"\"处理第day天的状态，计算第day+1天的状态\"\"\" if day >= self.deadline: return current_weather = self.weather[day] if day % 5 == 0: # 每5天打印一次进度 print(f\"处理第 {day} 天，天气: {current_weather}\") # 遍历当前天的所有区域 for area in list(self.dp[day].keys()): # 遍历该区域的所有状态 for (water, food), (money, prev_state) in list(self.dp[day][area].items()): # 如果已经到达终点，不需要继续处理 if area == self.end:  continue # 根据天气和区域，生成可能的行动 possible_actions = self.get_possible_actions(area, current_weather, day) # 处理每种可能的行动 for action in possible_actions:  self.process_action(day, area, water, food, money, prev_state, action) def get_possible_actions(self, area, weather, day): \"\"\"根据当前状态获取可能的行动\"\"\" actions = [] # 沙暴日只能停留 if weather == \"沙暴\": # 矿山特殊处理 if area in self.mines: # 判断是否是当天到达矿山（前一天不在此区域） is_new_arrival = self.is_new_arrival(day, area) if is_new_arrival:  actions.append(\"stay\") # 到达矿山当天只能普通停留 else:  actions.append(\"stay\") # 普通停留  actions.append(\"mine\") # 挖矿 else: actions.append(\"stay\") # 普通区域停留 else: # 非沙暴日可以移动或停留 # 添加移动到相邻区域的行动 for neighbor in self.graph[area]: actions.append(f\"move_{neighbor}\") # 添加停留行动 if area in self.mines: # 判断是否是当天到达矿山 is_new_arrival = self.is_new_arrival(day, area) if is_new_arrival:  actions.append(\"stay\") # 到达矿山当天只能普通停留 else:  actions.append(\"stay\") # 普通停留  actions.append(\"mine\") # 挖矿 else: actions.append(\"stay\") # 普通区域停留 return actions def is_new_arrival(self, day, area): \"\"\"判断是否是当天到达该区域（前一天不在此区域）\"\"\" if day == 0: return area == self.start # 第0天只有起点是初始位置 # 检查前一天是否在该区域有任何状态 return len(self.dp[day-1].get(area, {})) == 0 def process_action(self, day, area, water, food, money, prev_state, action): \"\"\"处理具体行动，更新下一天的状态\"\"\" next_day = day + 1 if next_day > self.deadline: return  current_weather = self.weather[day] base_consumption = self.get_base_consumption(day) # 计算资源消耗和下一区域 if action.startswith(\"move\"): # 移动到相邻区域，消耗2倍基础资源 next_area = int(action.split(\"_\")[1]) water_cost = 2 * base_consumption[\"water\"] food_cost = 2 * base_consumption[\"food\"] new_money = money elif action == \"stay\": # 普通停留，消耗基础资源 next_area = area water_cost = base_consumption[\"water\"] food_cost = base_consumption[\"food\"] new_money = money elif action == \"mine\": # 挖矿，消耗3倍基础资源，获得收益 next_area = area water_cost = 3 * base_consumption[\"water\"] food_cost = 3 * base_consumption[\"food\"] new_money = money + self.base_income # 挖矿收益 else: return # 检查资源是否足够 new_water = water - water_cost new_food = food - food_cost if new_water < 0 or new_food  0 and max_buy_water > 0: buy_water = min(needed_water, max_buy_water) new_m = money - buy_water * self.village_price[\"water\"] self.update_next_state(next_day, next_area, water + buy_water, food, new_m, prev_day, prev_area, prev_water, prev_food, action + \"_buy_water\") # 策略3：只购买食物（如果需要） if needed_food > 0: max_buy_food = min( needed_food, money // self.village_price[\"food\"], (self.max_weight - water * self.box_weight[\"water\"]) // self.box_weight[\"food\"] - food ) if max_buy_food > 0: buy_food = min(needed_food, max_buy_food) new_m = money - buy_food * self.village_price[\"food\"] self.update_next_state(next_day, next_area, water, food + buy_food, new_m, prev_day, prev_area, prev_water, prev_food, action + \"_buy_food\") # 策略4：同时购买水和食物（如果需要） if needed_water > 0 and needed_food > 0 and max_buy_water > 0: remaining_money_after_water = money - max_buy_water * self.village_price[\"water\"] if remaining_money_after_water > 0: max_buy_food = min(  needed_food,  remaining_money_after_water // self.village_price[\"food\"],  (self.max_weight - (water + max_buy_water) * self.box_weight[\"water\"]) // self.box_weight[\"food\"] - food ) if max_buy_food > 0:  new_m = remaining_money_after_water - max_buy_food * self.village_price[\"food\"]  self.update_next_state(next_day, next_area, water + max_buy_water, food + max_buy_food, new_m,  prev_day, prev_area, prev_water, prev_food, action + \"_buy_both\") def update_next_state(self, next_day, next_area, water, food, money, prev_day, prev_area, prev_water, prev_food, action): \"\"\"更新下一天的状态，保留最大资金\"\"\" if not self.is_valid_weight(water, food): return  state = (water, food) # 记录前序状态，用于回溯路径 previous_state = (prev_day, prev_area, prev_water, prev_food, action) # 只保留该状态下的最大资金 if state not in self.dp[next_day][next_area]: self.dp[next_day][next_area][state] = (money, previous_state) else: current_max_money = self.dp[next_day][next_area][state][0] if money > current_max_money: self.dp[next_day][next_area][state] = (money, previous_state) def trace_path(self, day, area, water, food, prev_state): \"\"\"回溯最优路径，收集数据用于Excel导出\"\"\" # 获取当前状态的资金 current_money = self.dp[day][area].get((water, food), [0, None])[0] # 避免重复记录同一日期 if not any(item[\'日期\'] == day for item in self.path_data): self.path_data.append({ \'日期\': day, \'所在区域\': area, \'剩余资金数\': current_money, \'剩余水量\': water, \'剩余食物量\': food }) if prev_state and day > 0: prev_day, prev_area, prev_water, prev_food, action = prev_state prev_state_data = self.dp[prev_day][prev_area].get((prev_water, prev_food), [0, None]) self.trace_path(prev_day, prev_area, prev_water, prev_food, prev_state_data[1]) def write_to_excel(self, filename): \"\"\"使用pandas将路径数据写入Excel\"\"\" # 创建包含所有日期的完整框架 all_days = pd.DataFrame({\'日期\': range(self.deadline + 1)}) # 将路径数据转换为DataFrame path_df = pd.DataFrame(self.path_data) # 合并数据，确保所有日期都存在 result_df = pd.merge(all_days, path_df, on=\'日期\', how=\'left\') # 确保列顺序正确 result_df = result_df[[\'日期\', \'所在区域\', \'剩余资金数\', \'剩余水量\', \'剩余食物量\']] # 写入Excel with pd.ExcelWriter(filename, engine=\'openpyxl\') as writer: result_df.to_excel(writer, sheet_name=\'最优路径\', index=False) # 调整列宽优化显示 worksheet = writer.sheets[\'最优路径\'] for col in worksheet.columns: column = col[0].column_letter # 获取列字母（如A、B、C） # 计算该列最大内容长度 max_length = max(len(str(cell.value)) for cell in col) + 2 worksheet.column_dimensions[column].width = max_length print(f\"路径已写入Excel文件：{filename}\") def find_best_result(self): \"\"\"找到到达终点的最优结果\"\"\" best_money = -1 best_day = self.deadline + 1 best_water = 0 best_food = 0 best_state = None # 检查所有在截止日期前到达终点的状态 for day in range(self.deadline + 1): if self.end in self.dp[day]: for (water, food), (money, prev_state) in self.dp[day][self.end].items():  # 计算最终资金（加上剩余资源退款）  final_money = money + water * self.base_price[\"water\"] / 2 + food * self.base_price[\"food\"] / 2  # 更新最优解  if (final_money > best_money or (final_money == best_money and day < best_day)): best_money = final_money best_day = day best_water = water best_food = food best_state = (water, food, prev_state) # 回溯最优路径 if best_state: self.trace_path(best_day, self.end, best_state[0], best_state[1], best_state[2]) return { \"截止日期\": self.deadline, \"到达时间\": best_day if best_day <= self.deadline else \"超时\", \"剩余水\": best_water, \"剩余食物\": best_food, \"最终资金\": round(best_money) if best_money != -1 else 0, \"路径数据\": self.path_data.copy() # 保存路径数据 } def solve(self): \"\"\"求解问题的主函数\"\"\" # 初始化第0天状态 print(\"初始化第0天状态...\") self.initialize_dp() # 处理每一天 for day in range(self.deadline): self.process_day(day) # 找到最优结果 print(\"寻找最优结果...\") return self.find_best_result()def calculate_shortest_path(graph, start, end): \"\"\"用BFS计算两点间最短路径（步数）\"\"\" if start == end: return 0 visited = {start: 0} # 记录到达每个节点的最少步数 queue = deque([start]) while queue: current = queue.popleft() current_steps = visited[current] for neighbor in graph[current]: if neighbor not in visited: visited[neighbor] = current_steps + 1 queue.append(neighbor) if neighbor == end:  return visited[neighbor] # 找到终点，返回最少步数 return float(\'inf\') # 无法到达终点def calculate_min_mine_days(graph, start, end, mines): \"\"\"计算多矿区场景下的挖矿最少必要时间（取所有矿区的最小值）\"\"\" min_days = float(\'inf\') for mine in mines: # 起点到矿区的最短时间 M = calculate_shortest_path(graph, start, mine) # 矿区到终点的最短时间 E = calculate_shortest_path(graph, mine, end) # 单个矿区的最少时间：到矿区 + 1天停留 + 1天挖矿 + 到终点 mine_min_days = M + 2 + E # 2 = 1停留 + 1挖矿 if mine_min_days  valid_end: print(\"错误：最短路径天数超过30天，无有效截止日期\") exit() # 第一阶段：d < min_mine_days（只能纯赶路，无法挖矿） print(f\"\\n===== 测试截止日期: {valid_start}天（仅纯赶路） =====\") game = DesertCrossing(valid_start) result = game.solve() all_results.append(result) print(f\"当前结果: 最终资金={result[\'最终资金\']}\") # 第二阶段：d ≥ min_mine_days（可挖矿+纯赶路，比较最优策略） phase2_start = max(min_mine_days, valid_start) if phase2_start <= valid_end: for deadline in range(phase2_start, valid_end + 1): print(f\"\\n===== 测试截止日期: {deadline}天（可挖矿） =====\") game = DesertCrossing(deadline) result = game.solve() all_results.append(result) print(f\"当前结果: 最终资金={result[\'最终资金\']}\") # 3. 筛选全局最优方案 if not all_results: print(\"无有效结果\") exit() best_overall = max(all_results, key=lambda x: (x[\"最终资金\"])) # 4. 输出最优方案详情 print(\"\\n\\n===== 全局最优方案 =====\") print(f\"最优截止日期: {best_overall[\'截止日期\']}天\") print(f\"到达终点时间: {best_overall[\'到达时间\']}天\") print(f\"最大最终资金: {best_overall[\'最终资金\']}元\") print(f\"剩余水: {best_overall[\'剩余水\']}箱\") print(f\"剩余食物: {best_overall[\'剩余食物\']}箱\") # 导出最优路径 best_game = DesertCrossing(deadline=best_overall[\'截止日期\']) best_game.path_data = best_overall[\'路径数据\'] best_game.write_to_excel(f\"第一关最优路径_截止日期{best_overall[\'截止日期\']}天.xlsx\")

运行结果如图：

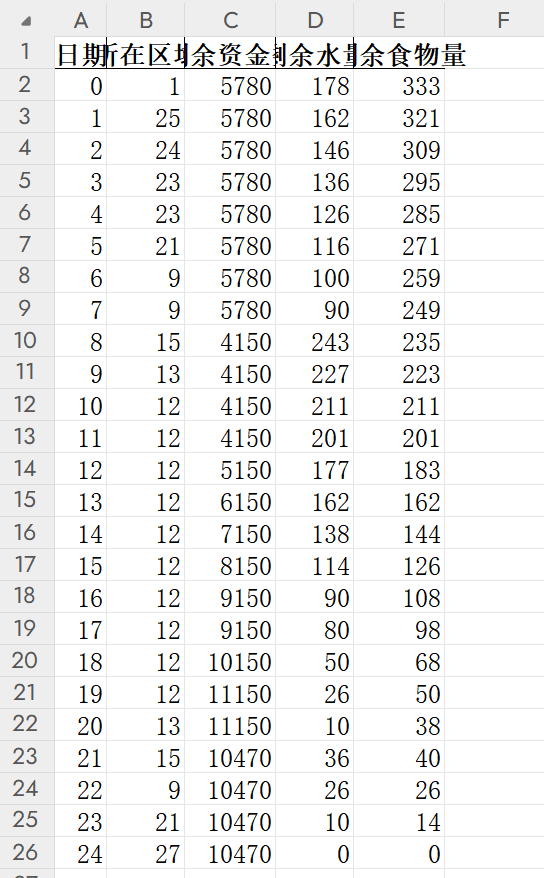
        【果然，人还是要勇敢一回啊！】

        课后作业：完成第二关的代码编写并弄明白原理！

        有同学可能会问了：主播主播，后面两题怎么办。主播表示：答案就在开头！

        好了，同学们，快乐的时光总是短暂的，今天的学习到这里就已经全部结束啦！

        如果本文让你有所收获的话，请一键三连呀！

        相逢即是缘分，点个赞再走吧！！！