网站导航
> 技术文档 > 【A题解题思路】2025华数杯数学建模A题解题思路+可运行代码参考（无偿分享）

【A题解题思路】2025华数杯数学建模A题解题思路+可运行代码参考（无偿分享）

网友: 技术文档 2025-09-02 19:12:52

注：该内容由“数模加油站”原创，无偿分享，可以领取参考但不要利用该内容倒卖，谢谢！

A 题  多孔膜光反射性能的优化与控制

在问题一中，参赛者的任务是从原始实验数据出发，分析温度、湿度、固含量三个变量对孔面积占比这一重要响应变量的影响趋势。这是一次典型的实验数据初步分析任务，重点在于构建经验性建模框架，比如可以考虑多元线性模型或带有交互项的多项式模型，并通过残差分析、拟合优度（如 $R^2$）等方式检验模型的合理性。这一阶段强调“由现象找规律”。

问题二则是在已有经验模型的基础上，进一步探讨孔结构特征（即孔面积占比）与膜光反射性能之间的数学关系。它从一个新的物理视角切入，即认为孔隙结构影响材料的光学性质，从而引出介电模型 + 反射率模型的建立。这是本题的“物理建模核心”，要求参赛者具备一定的光学理论背景，如利用介电常数、反射率的计算公式、膜层多孔率等原理，建立由“制备条件 → 孔隙结构 → 光学性能”的因果通路。该部分的建模过程理论性较强，是整题的科学性支点。

在问题三中，任务回归到“优化”这一经典建模目标上：如何通过调节实验参数（温度、湿度、固含量）来实现孔面积占比的最大化。这是典型的约束优化问题，可采用数学规划方法（如最小化负值、数值搜索等）求得最优点。参赛者不仅要利用前述模型表达响应函数，还要关注参数空间是否存在合理物理限制，优化过程是否收敛，所得结果是否具备实验可行性。

最后，问题四回到建模的逻辑原点——模型变量的合理性判断。这一问强调科研的“反思性与迭代性”：模型并非一次性完成，而是需要基于数据反馈进行检验与优化。任务要求通过统计手段（如相关性分析、变量重要性排序、显著性检验）剖析变量的重要性，并据此“改写或简化模型结构”。这不仅能提升模型精度与可解释性，也有助于后续实验推广。最后，还需要重新执行优化过程，并与问题三进行对比，体现模型修正带来的结果改进或结构稳健性。

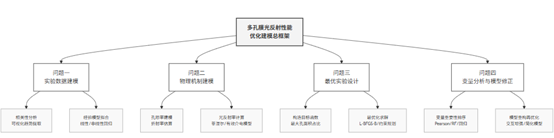
思路框架图

问题1 多孔膜孔面积占比的理论模型构建

问题1思路框架：

1. 概述：物理过程与建模框架总览

多孔膜的孔结构特征，尤其是孔面积占比，是其光反射性能的关键决定因素。该结构在多孔膜的制备过程中逐步演化形成，主要受控于DMF的蒸发、环丁砜与纤维素的析出、液滴的扩散、碰撞及融合等多重物理机制。因此，为了构建准确刻画孔面积占比的理论模型，我们必须深入剖析这些互相关联的机制，并建立数学模型将其一一表达。

整体来看，这一过程是一个典型的“自下而上”的物理系统演化：
从微观粒子的溶解与分布出发，经过中尺度的运动与碰撞，最终在宏观尺度上表现为多孔膜的结构参数。故本题采用模块化建模思路，将整个制备过程划分为六个核心环节，每个环节建立对应数学子模型，最终整合为整体系统的控制方程。

2. 蒸发动力学模型：DMF挥发行为的建模

多孔膜的初始成分为DMF（溶剂）、环丁砜（非溶剂）与醋酸纤维素（聚合物）组成的混合液。制备过程首先由DMF的蒸发驱动体系浓度不断变化，从而影响后续析出与结构转变。

我们令：

  • m_D(t)：时间t时刻DMF的质量；
  • v_{\\text{vap}}：单位时间DMF的蒸发速率；
  • c_D = \\frac{m_D}{V_{\\text{sol}}}：DMF浓度；
  • T：环境温度，H：相对湿度（取值 0 \\sim 1）；
  • k_1：与扩散/对流相关的挥发性常数；
  • k_h：湿度调节系数；
  • P_{\\text{sat}}(T)：温度T时DMF的饱和蒸气压；
  • P_{\\text{amb}}：环境蒸气压（设为0）

DMF蒸发可由下式建模：

\\frac{dm_D}{dt} = -v_{\\text{vap}} = -k_1 \\cdot (1 - k_h \\cdot H) \\cdot c_D \\cdot P_{\\text{sat}}(T)

其中，P_{\\text{sat}}(T)由 Antoine 方程计算：

\\log_{10}(P_{\\text{sat}}) = A - \\frac{B}{C + T}

这一模型反映了温度升高或湿度降低均会加快DMF蒸发，从而加速体系演化。

3. 溶质析出模型：溶解度控制的质量平衡分析

DMF的蒸发导致溶液中溶质（环丁砜和纤维素）的相对浓度不断上升，进而超过溶解度极限，诱发析出。

定义：

  • S_S：DMF对环丁砜的质量溶解度；
  • S_C：DMF对醋酸纤维素的质量溶解度；
  • m_D：当前DMF质量；
  • m_S、m_C：环丁砜、纤维素的初始质量；
  • m_{S,\\text{precip}}、m_{C,\\text{precip}}：各自析出质量；

析出模型如下：

环丁砜：

m_{S,\\text{precip}} = \\max(0,\\ m_S - m_D \\cdot S_S)

醋酸纤维素：

m_{C,\\text{precip}} = \\max(0,\\ m_C - m_D \\cdot S_C)

这一模型基于质量平衡假设，忽略相互溶解影响，为后续液滴形成与运动模型提供输入。

4. 液滴扩散模型：小液滴的布朗运动建模

析出的环丁砜通常以小液滴形式悬浮在溶液中，并进行布朗运动，其扩散行为是驱动后续碰撞与融合的关键动力来源。

根据斯托克斯-爱因斯坦公式：

D = \\frac{k_B T}{6 \\pi \\eta r}

其中：

  • D：扩散系数；
  • k_B：玻尔兹曼常数；
  • \\eta：体系粘度；
  • r：小液滴半径。

扩散速度可近似表达为：

v_{\\text{drop}} \\propto \\sqrt{D} = \\sqrt{\\frac{k_B T}{6 \\pi \\eta r}}

考虑粘度受纤维素浓度影响，引入爱因斯坦粘度修正：

\\eta = \\eta_0 \\cdot (1 + 2.5 \\phi)

\\phi = \\frac{V_{\\text{precip,C}}}{V_{\\text{sol}}}：纤维素体积分数

最终：

v_{\\text{drop}} = \\alpha_1 \\cdot \\sqrt{\\frac{k_B T}{6 \\pi \\eta_0 (1 + 2.5 \\phi) r}}

该式揭示温度升高或粘度下降均将提高扩散能力，加快粒子碰撞频率。

5. 小液滴碰撞模型：大液滴的初始形成机制

运动中的小液滴因随机碰撞而融合，生成大液滴。这一过程可用经典的分子碰撞理论建模。

设：

  • n：小液滴数密度；
  • \\sigma：小液滴等效直径；
  • v_{\\text{drop}}：小液滴平均速度；
  • \\Delta m：每次融合的平均质量增量；
  • \\beta_1：融合概率与效率的常数。

碰撞频率为：

f = 2 n \\sigma^2 v_{\\text{drop}}

单位时间内形成的大液滴质量：

\\frac{d m_{\\text{big1}}}{dt} = \\beta_1 \\cdot f \\cdot \\Delta m = \\beta_1 \\cdot 2 n \\sigma^2 v_{\\text{drop}} \\cdot \\Delta m

该部分建模主要受小液滴浓度与扩散速度主导。

6. 大液滴增长模型：小液滴吸附行为建模

当形成的大液滴逐渐长大，它们可进一步通过吸附小液滴而增大质量。

设：

  • S：所有大液滴的总表面积；
  • v_{\\perp} \\approx v_{\\text{drop}}：垂直运动速度；
  • m_S：单位小液滴质量；
  • n：小液滴数密度；
  • \\beta_2：碰撞吸附效率常数；

有：

\\frac{d m_{\\text{big2}}}{dt} = \\beta_2 \\cdot S \\cdot v_{\\perp} \\cdot n \\cdot m_S

若假设 S \\propto m_{\\text{big}}^{2/3}，则得：

\\frac{d m_{\\text{big}}}{dt} = \\beta_1 \\cdot f \\cdot \\Delta m + \\beta_2 \\cdot m_{\\text{big}}^{2/3} \\cdot v_{\\text{drop}} \\cdot n \\cdot m_S

此为系统演化中最关键的非线性微分方程，捕捉液滴群体从小至大的动态增长。

7. 孔结构模型：孔面积占比的表达公式

大液滴在制膜后被冲洗去除，其所在区域留下一定尺寸的孔洞，对应最终膜的孔面积占比。

设：

  • A_{\\text{pore}}：孔面积占比；
  • m_{\\text{big,final}}：最终大液滴总质量；
  • \\gamma：比例系数（由液滴体积与孔面积映射关系推导）

则有：

A_{\\text{pore}} = \\gamma \\cdot m_{\\text{big,final}}

最终模型形式：

A_{\\text{pore}} = f(T, H, SC;\\ \\mathbf{k})

其中 \\mathbf{k} 是由多个待定常数组成的系数向量，包括挥发系数、碰撞概率、吸附系数等。

8. 模型合理性与简化假设讨论

在本模型构建过程中，为确保可计算性与逻辑清晰性，我们做出了若干假设：

  1. 液滴均为球形，忽略界面张力影响；
  2. 粘度仅由析出纤维素控制，环丁砜贡献较小；
  3. 忽略小液滴生成的孔，仅考虑大液滴对孔结构的贡献；
  4. 每阶段参数为准定态常数，未处理全过程瞬态微分（可在问题二扩展）；

我们已构建出一个完整的、分阶段、多参数联动的多孔膜孔结构形成理论模型。它能系统刻画制备条件与最终结构之间的非线性耦合关系，并为后续参数拟合与实验优化提供理论支撑。

Python代码：

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom scipy.optimize import least_squaresfrom mpl_toolkits.mplot3d import Axes3D# 设置中文字体和负号显示plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']plt.rcParams[\'axes.unicode_minus\'] = False# 读取数据file_path = \"/mnt/data/附件2.xlsx\"df = pd.read_excel(file_path)# 显示前几行数据df.head()# 尝试读取非空行，跳过前几行说明性文字df_clean = pd.read_excel(file_path, skiprows=5)# 显示数据头部，确认字段df_clean.head()# 尝试跳过更多说明文字，只读取后面的表格数据部分df_data = pd.read_excel(file_path, skiprows=10)# 显示前几行以确认字段名df_data.head(10)# 第0行为列名，需要将其作为表头，重新读取数据df_data = pd.read_excel(file_path, skiprows=11, names=[\"编号\", \"温度\", \"湿度\", \"固含量\", \"孔面积占比\"])# 将各字段转换为数值型df_data = df_data.apply(pd.to_numeric, errors=\'coerce\')# 丢弃含NaN的行df_data.dropna(inplace=True)# 显示清洗后的数据df_data.head()# 计算每组实验（相同 T、H、SC）对应的孔面积占比平均值grouped = df_data.groupby([\'温度\', \'湿度\', \'固含量\'])[\'孔面积占比\'].mean().reset_index()grouped.rename(columns={\'孔面积占比\': \'平均孔面积占比\'}, inplace=True)# 显示处理后的数据grouped.head()# 构建用于拟合的输入输出数据X = grouped[[\'温度\', \'湿度\', \'固含量\']].valuesy = grouped[\'平均孔面积占比\'].values# 定义简化后的模型（经验形式）用于拟合def predict_A(params, X): # 参数解包 a, b, c, d, e, f = params T, H, SC = X[:,0], X[:,1]/100, X[:,2] # 温度，湿度比例，固含量 return a*T + b*H + c*SC + d*T*SC + e*T*H + f# 构建残差函数def residuals(params, X, y): return predict_A(params, X) - y# 初始参数猜测initial_params = np.zeros(6)# 最小二乘拟合result = least_squares(residuals, initial_params, args=(X, y))# 拟合结果fitted_params = result.xfitted_params

后续都在“数模加油站”......

网络标签：

相关问题