LeetCode刷题——动态规划2

题目1：分割等和子集

题目：

问题分析：因为在分割数组的时候，每个元素只能取一次，这可以看成一个01背包问题。01背包问题中的物品种类N和背包重量M，在这一题中都可以看做是总和的一般target，每个物品的重量weight[i]和价值value[i]也是相等的，都是nums[i]。在内层循环中，j>=nums[i]这个作为判断循环的停止的条件是因为，当j<nums[i]时，dp[j-nums[i]]就没有意义了。内层循环从大到小遍历是为了保证每个元素nums[i]只被放进一次。假设从小到大遍历的话，dp[1]=Math.max(dp[1],dp[1-nums[0]]+nums[0])=Math.max(dp[1],dp[1-1]+1)=1,dp[2]=Math.max(dp[2],dp[2-nums[0]]+nums[0])=Math.max(dp[2],dp[2-1]+1)=2，此时的元素nums[0]=1被放进了两次是没有意义的。

代码：

class Solution { public boolean canPartition(int[] nums) { int target;//总和的一半，作为重量和价值的目标 int sum=0; for(int num:nums){ sum+=num; } if(sum%2!=0) return false;//此举是为了说明当总和不能被2整除时无法分 target=sum/2; int[] dp=new int[target+1];//映射为01背包问题，此题中的重量和价值相等 for(int i=0;i=nums[i];j--){ dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]); } if(dp[target]==target) return true; } return false; }}

时间复杂度：O(N*target).

题目2：最后一块石头的重量II

题目：

问题分析：这道题的本质就是把这堆石头分成两堆总重量都很靠近所有石头总质量的二分之一，然后再求这两堆石头的总重量之差，这就与题目1：分割等和子集的解题思路一致了。

代码：

class Solution { public int lastStoneWeightII(int[] stones) { int sum=0; for(int stone:stones){ sum+=stone; } int target=sum/2; int[] dp=new int[target+1]; for(int i=0;i=stones[i];j--){ dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]); } } return sum-2*dp[target]; }}

时间复杂度：O(N*target).

题目3：目标和

题目：

问题分析：这道题就是将数组nums中的元素整体分为两堆left和right，同时在一堆前加负号，即left-right=target.但是同时left+right=sum（sum是整个数组元素的总和）。所以right=sum-left，  left-(sum-left)=target，所以left=(sum+target)/2，所以此题就转换为了用数组元素装满背包容量为left的01背包问题。二维数组dp[i][j]表示用下标0到i装满背包容量为j的方法数，dp[i][j]可以由两种方法得到，一种是不装下标为i的元素，即dp[i][j]=dp[i-1][j]；另一种是装下标为i的元素，那么背包容量j就要给下标为i的元素空出大小为nums[i]的空间，即dp[i][j]=dp[i-1][j-nums[i].所以                    dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]]。由这个递归公式，所以应该初始化dp数组的最上面和最左面的元素。dp[0][0]=1,因为装满背包容量为0的背包的方法是不放物品0（前提是物品0的值不为0）。dp[0][num[0]]=1,用物品0装满背包容量为nums[0]的背包的方法也只有一个。dp[i][0]的数值要看下标从0到i的数组元素有几个0，因为每个0都面临两种放进背包容量为0的选择，即放或不放，假设有t个0，所以dp[i][0]=2^t。

代码：

class Solution { public int findTargetSumWays(int[] nums, int target) { int sum=0;//用于计算数组总和 for(int i:nums){ sum+=i; } if((sum+target)%2!=0) return 0;//表示找不到任何一种方法 if(Math.abs(target)>sum) return 0; int left=(sum+target)/2; int[][] dp=new int[nums.length][left+1]; dp[0][0]=1;//用物品0装满背包容量为0的书包的唯一一种方法就是什么都不装 if(nums[0]<=left) dp[0][nums[0]]=1; int zeroNum=0;//统计数组中0的个数 for(int i=0;i<nums.length;i++){ if(nums[i]==0) zeroNum++; dp[i][0]=(int)Math.pow(2,zeroNum); } for(int i=1;i<nums.length;i++){ for(int j=0;jj) dp[i][j]=dp[i-1][j]; else dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]]; } } return dp[nums.length-1][left]; }}

时间复杂度：O(N*sum)。

题目4：一和零

题目：

问题分析：因为每个字符串只能放进子集中一次，所以这可以看做是一个01背包问题。只是这个背包的容量是由两个维度构成的，一个是0的总个数m，一个是1的总个数n，本质都是背包的容量。数组dp[i][j]表示最多含有i个0和j个1的子集的长度，所以dp[i][j]=Math.max(dp[i][j],dp[i-zero][j-one]),其中的zero和one表示当前字符串中0的个数和1的个数。

代码：

class Solution { public int findMaxForm(String[] strs, int m, int n) { int[][] dp=new int[m+1][n+1];//表示最多有m个0和n个1的子集的长度 int zero; int one; for(String str:strs){ zero=0; one=0; for(char c:str.toCharArray()){ if(c==\'0\') zero++; else one++; } for(int i=m;i>=zero;i--){ for(int j=n;j>=one;j--){  dp[i][j]=Math.max(dp[i][j],dp[i-zero][j-one]+1); } } } return dp[m][n]; }}

时间复杂度：O(MNK)

题目5：完全背包问题

题目：

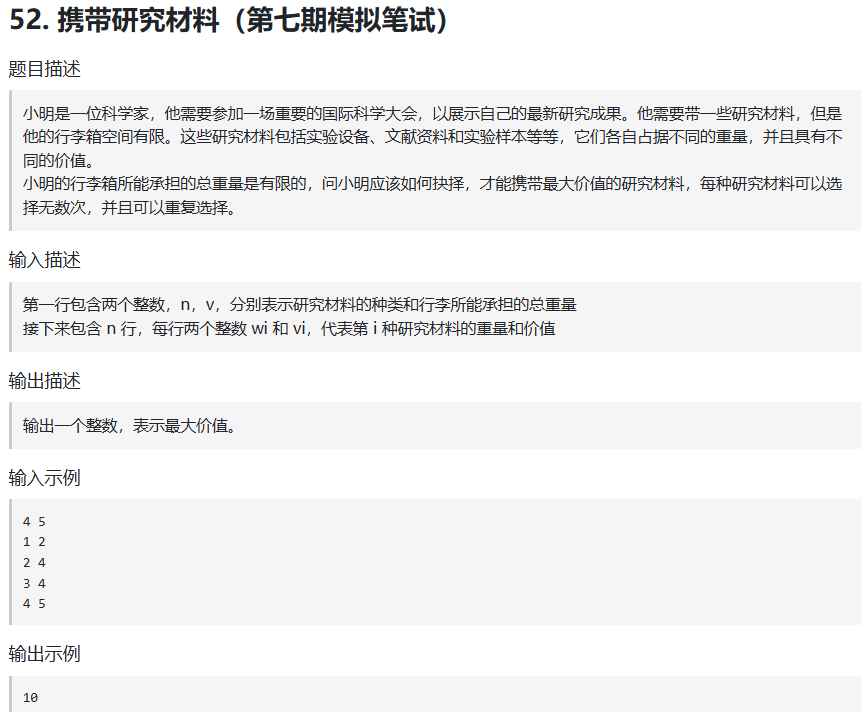
问题分析：01背包问题是每个物品只能被放进背包一次，每个物品也只存在一个。完全背包问题每个物品可以被放进背包多次，即每样物品存在多个。数组dp[i][j]表示下标为0到i的物品装进背包容量为j的背包所能获得的最大价值。dp[i][j]也有两种得到的方式：①不放物品i ②放物品i .①不放物品i:则dp[i][j]=dp[i-1][j]。②放物品i：即从容量为j的背包中空出物品i的总量weight[i]，剩下的容量为j-weight[i]，但注意的是，与01背包问题不同的是，完全背包问题中的物品可以多次被放进背包中，所以剩下的j-weight[i]的容量放的物品下标依旧是从0到i，即dp[i][j]=dp[i][j-weight[i]]。这两种情况合到一起就是：dp[i][j]=Math.max(dp[i-1][j],dp[i][j-weight[i]]).因为得到dp[i][j]一个来自i-1,一个来自j-weight[i],所以初始化的时候要考虑dp[0][j]和dp[i][0]。dp[i][0]=0，因为背包的容量为0，它的最大价值也为0. dp[0][j]要根据j与物品0的重量weight[0]的数量关系来初始化，jweight[0],dp[0][j]=dp[0][j-weight[0]]+value[0]

代码：

import java.util.Scanner;public class Main{ public static void main(String[] args){ Scanner sc=new Scanner(System.in); int n=sc.nextInt(); int m=sc.nextInt(); int[] weight=new int[n]; int[] value=new int[n]; for(int i=0;i<n;i++){ weight[i]=sc.nextInt(); value[i]=sc.nextInt(); } int[][] dp=new int[n][m+1]; for(int i=0;i<n;i++){ dp[i][0]=0; } for(int j=weight[0];j<=m;j++){ dp[0][j]=dp[0][j-weight[0]]+value[0]; } for(int i=1;i<n;i++){ for(int j=0;j<=m;j++){ if(j<weight[i]) dp[i][j]=dp[i-1][j]; else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-weight[i]]+value[i]); } } sc.close(); System.out.println(dp[n-1][m]); } }

时间复杂度：O(N*m)

题目6：零钱兑换II

题目：

问题分析：dp[i][j]表示使用下标从0到i的coins[i]凑满总金额为j的方法数。这道题与题目3：目标和这道题很类似，只是题目3是01背包问题，本题是完全背包问题。所以递归关系式为                  dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]]也是由两部分组成的，①不放下标为i的硬币 ②放下标为i的硬币，留出下标i的空间coins[i],由于每个硬币可以放无数个，所以下标还是由0到i。初始化的时候，    dp[i][0]=1，凑满总金额为0的只有一种方法，那就是什么硬币都不放。当j能整除coins[0]的时候，dp[0][j]=1。

代码：

class Solution { public int change(int amount, int[] coins) { int n=coins.length; int[][] dp=new int[n][amount+1]; for(int i=0;i<n;i++){ dp[i][0]=1; } for(int j=0;j<=amount;j++){ if(j%coins[0]==0) dp[0][j]=1; } for(int i=1;i<n;i++){ for(int j=0;j<=amount;j++){ if(j<coins[i]) dp[i][j]=dp[i-1][j]; else dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]]; } } return dp[n-1][amount]; }}

时间复杂度：O(n*m)

题目7：组合总和IV

题目：

问题分析：这道题本质是一道排列的题目，数组元素dp[i]表示总和为i的排列的个数，所以dp[i]=dp[i]+dp[i-nums[j]],也是看成不加入nums[j]和加入nums[j]两种情况。因为求得是排列，所以先遍历数组元素还是先遍历总和的顺序就变得很重要了。先遍历数组元素再遍历总和，元素按固定顺序被处理，下标大的一定会出现在下标小的的后面，这就是传统的组合问题。先遍历总和再遍历数组元素，每个容量会被所有物品反复更新，允许 “先小物品后大物品” 和 “先大物品后小物品” 两种情况，因此是排列。

代码：

class Solution { public int combinationSum4(int[] nums, int target) { int[] dp=new int[target+1]; dp[0]=1; for(int j=0;j<=target;j++){ for(int i=0;i=nums[i]) dp[j]+=dp[j-nums[i]]; } } return dp[target]; }}

时间复杂度：O(N*T)

题目8：爬楼梯（进阶版）

题目：

问题分析：这道题本质也是一个排列问题，和题目7：组合总和IV题目类似。这道题把一次性爬1阶，2阶....m阶看做是物品的重量，把n阶看做是背包的容量。所以dp[i]表示爬i阶到楼顶一共有dp[i]种方法，dp[i]+=dp[i-j]，j从1到m，因为求得是排列，所以遍历的顺序很重要，要先遍历到楼顶总数，再遍历每次拍的楼梯阶数。

代码：

import java.util.Scanner;public class Main{ public static void main(String[] args){ Scanner sc=new Scanner(System.in); int n=sc.nextInt(); int m=sc.nextInt(); int[] dp=new int[n+1]; dp[0]=1; for(int i=1;i<=n;i++){ for(int j=1;j=j)dp[i]+=dp[i-j]; } } sc.close(); System.out.println(dp[n]); }}

时间复杂度：O(mn)