动态规划基本算法

动态规划思想

        动态规划的基本思想主要体现在将复杂问题分解、求解并记录子问题解、利用解之间的关系找到最优解等。

        动态规划通常会创建一个数组（可以是一维、二维甚至多维数组）来存储问题在不同阶段或状态下的解，数组中的每个位置对应一个特定的状态，后面的状态通过前面已计算出的状态来确定，可以理解为状态转移(递推)。

动态规划核心

• 状态定义：明确问题的状态表示。

• 状态转移方程：建立递推关系，描述状态之间的转移。

• 初始条件：确定递推的起点。

• 计算顺序：按特定顺序计算状态，避免重复计算。

动态规划相关例题

最长回文子串(leetcode.5)

string longestPalindrome(string s) { int n=s.size(); vector<vector>dp(n,vector(n)); for(int i=0;i<n;i++){ dp[i][i]=1; } int maxlen=1; string res; res+=s[0]; for(int len=2;len<=n;len++){ for(int l=0;l=n){  break; } if(s[l]==s[r]){  if(r-l>1){ dp[l][r]=dp[l+1][r-1];  }else{ dp[l][r]=1;  } } if(dp[l][r]&&(maxlen<(r-l+1))){  res=s.substr(l,(r-l+1));  maxlen=(r-l)+1; } } } return res; }

可以由图来理解，我们可以设置为两个指针，L,R，分别为最左侧和最右侧,len就是判断的长度，

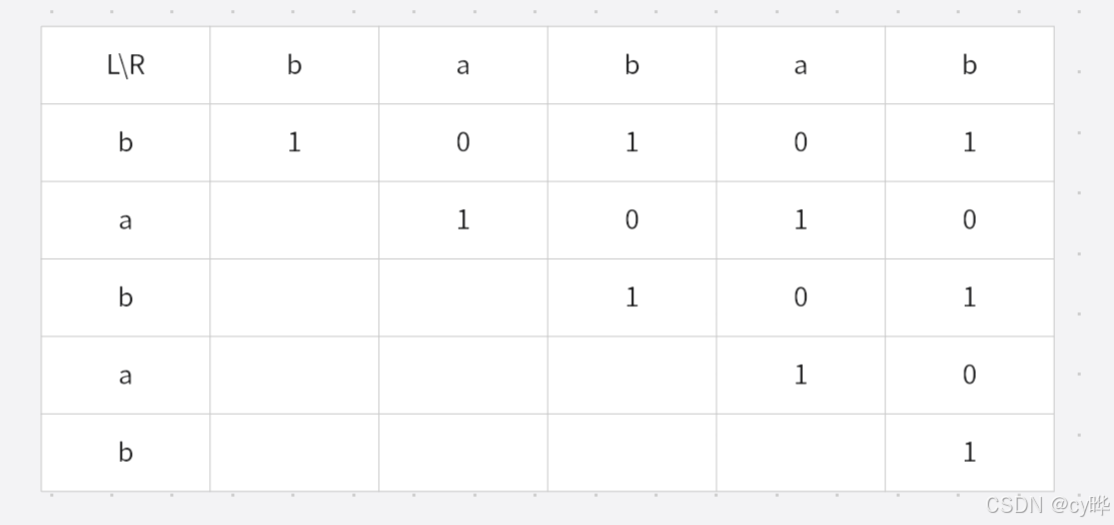
L可以理解为起点，1就是符合回文子串，而0就是不符合回文子串，每一个位置意味着存储是否是回文子串，举一个例子:

        从2行3列来看,最左侧L是b,，右侧R是b，而中间的字符只有一个a，那么从数组上看怎么判断bab是回文子串.

        bab的状态存储在2行3列，表示起点L为b，终点R为b,意思是判断最左侧是b，最右侧是b的字符串是否是回文子串，如果是就赋值为1，否则为0

        核心思想:当L和R相等时，就可以判断是否是回文子串了，就需要看L,R中间字符串或单个字符的状态(单个字符直接算回文字符串)。bab,最后一个b需要看的是a的状态，通过二维数组来观察，a的状态存储再dp[1][1]中，dp[1][1]=1,那么再R=L的前提下，dp[L][R]也为1

公式可以理解为:

dp[L][R]=dp[L+1][R-1]     R-L>1 (超过两个以上的字符需要判断中间字符是否回文)

dp[L][R]=1;                      R-L=1(只有两个字符，L和R所对应的字符相等直接是回文字符串)

（可以理解为通过前一个数组元素位置的状态来确定本身元素的状态）状态转移

接雨水(leetcode.42)

int trap(vector& height) { int n=height.size(); vector l(n),r(n); if(n==0)return 0; l[0]=height[0]; r[n-1]=height[n-1]; for(int i=1;i=0;i--)//求右侧柱子最高点 { r[i]=max(r[i+1],height[i]); } int sum=0; for(int i=1;i<n;i++) { sum+=min(l[i],r[i])-height[i];//当前位置左右侧选取两侧最高点中较低的位置求水柱长 } return sum; }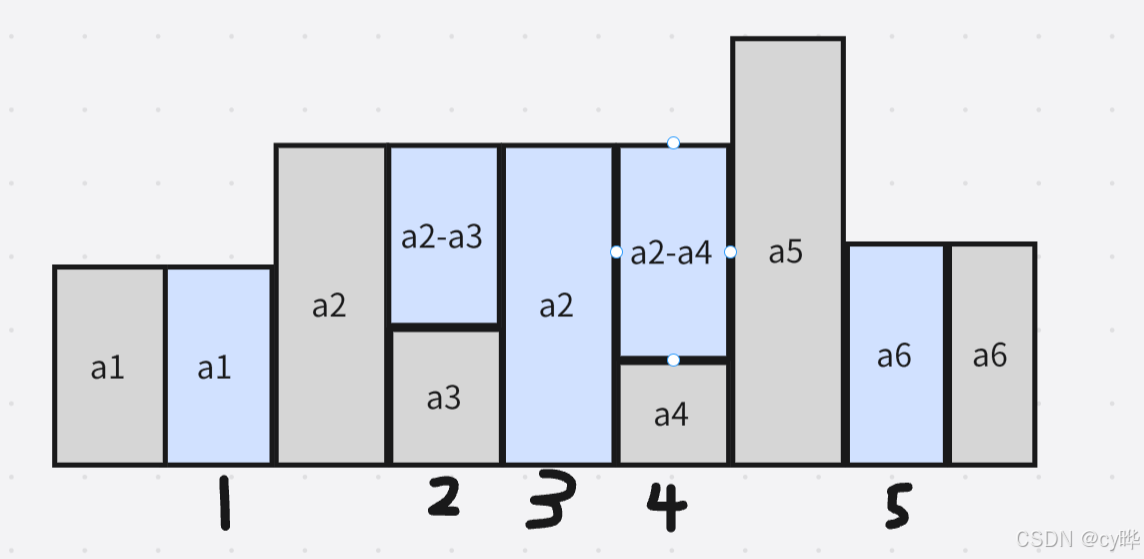

分为两个数组分别是L和R分别来存储每个点从左看的最高点和从右看的最高点

        求每经过一个点所拥有的水量实质上是当前这个点所能达到的最高值减去所在位置下面灰色柱子的长度，所以这道题核心上是求这个点所能达到的最高值

        例如水柱1所在的位置，他所能达到的最高点位置是a1,水柱2,3,4所在的位置所能达到最高点位置是a2,水柱5就是a6。

可以用一个公式来概括求每个水柱所能达到的最高点min(max(L[i]),max(R[i]));

最终结果就是min(max(L[i]),max(R[i]))-height[i]->达到的最高点减去下方灰柱子高度

而这就需要用两个数组L，R分别存储当前位置左侧和右侧所经历过的最高灰柱的高度

不同路径(leetcode.62)

        实质思想就是当前路径的可能路线等于上方路径的可能路线加上左侧路径的可能路线，最左侧和最上侧只有一条路线

int uniquePaths(int m, int n) { vector<vector> dp(m,vector(n)); for(int i=0;i<m;i++){ dp[i][0]=1; } for(int j=0;j<n;j++){ dp[0][j]=1; } for(int i=1;i<m;i++){ for(int j=1;j<n;j++){ dp[i][j]=dp[i-1][j]+dp[i][j-1]; } } return dp[m-1][n-1]; }

动态规划之背包问题

典型背包问题