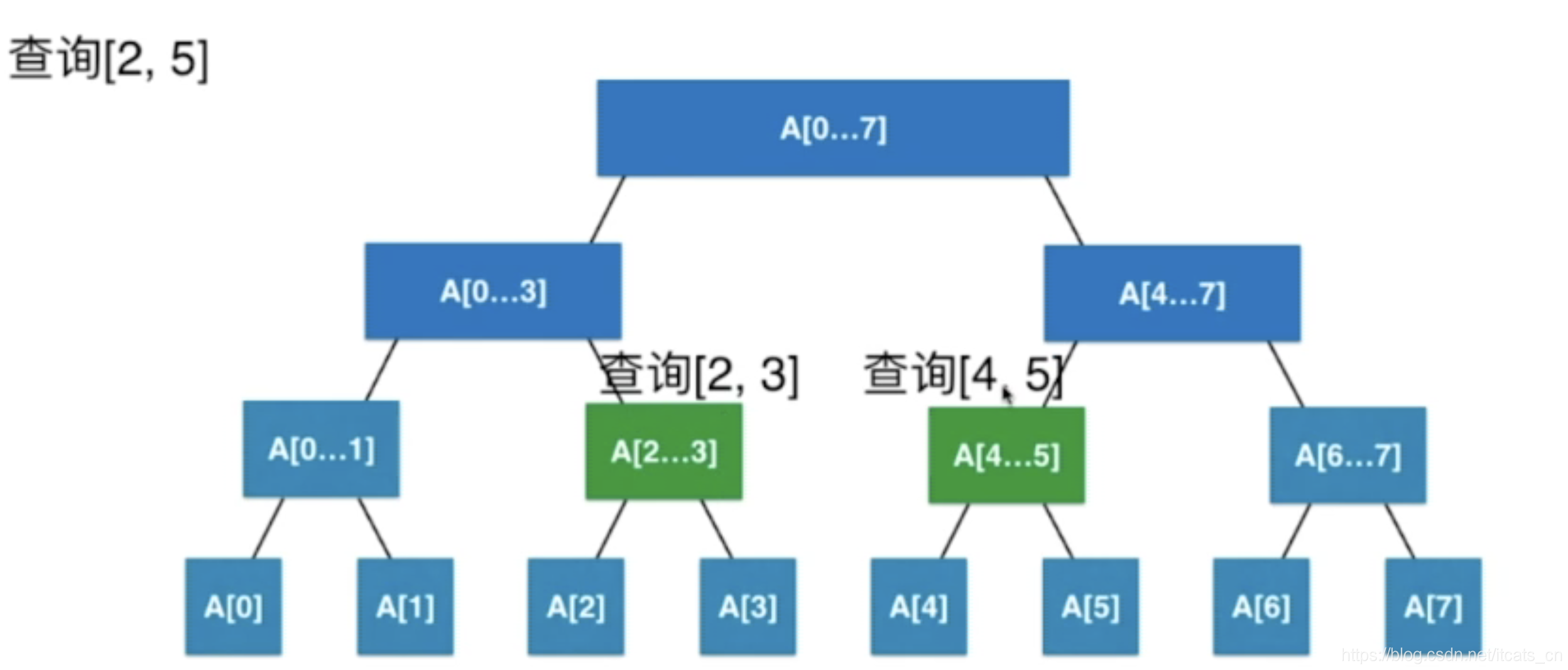
《算法导论》第 14 章 - 数据结构的扩张

        大家好！今天我们来深入学习《算法导论》第 14 章 —— 数据结构的扩张。这一章主要介绍了如何基于现有数据结构（如二叉搜索树）扩展出新的功能，以满足更复杂的问题需求。我们会从动态顺序统计树讲到区间树，每个知识点都会配上完整可运行的 C++ 代码，方便大家动手实践。

思维导图

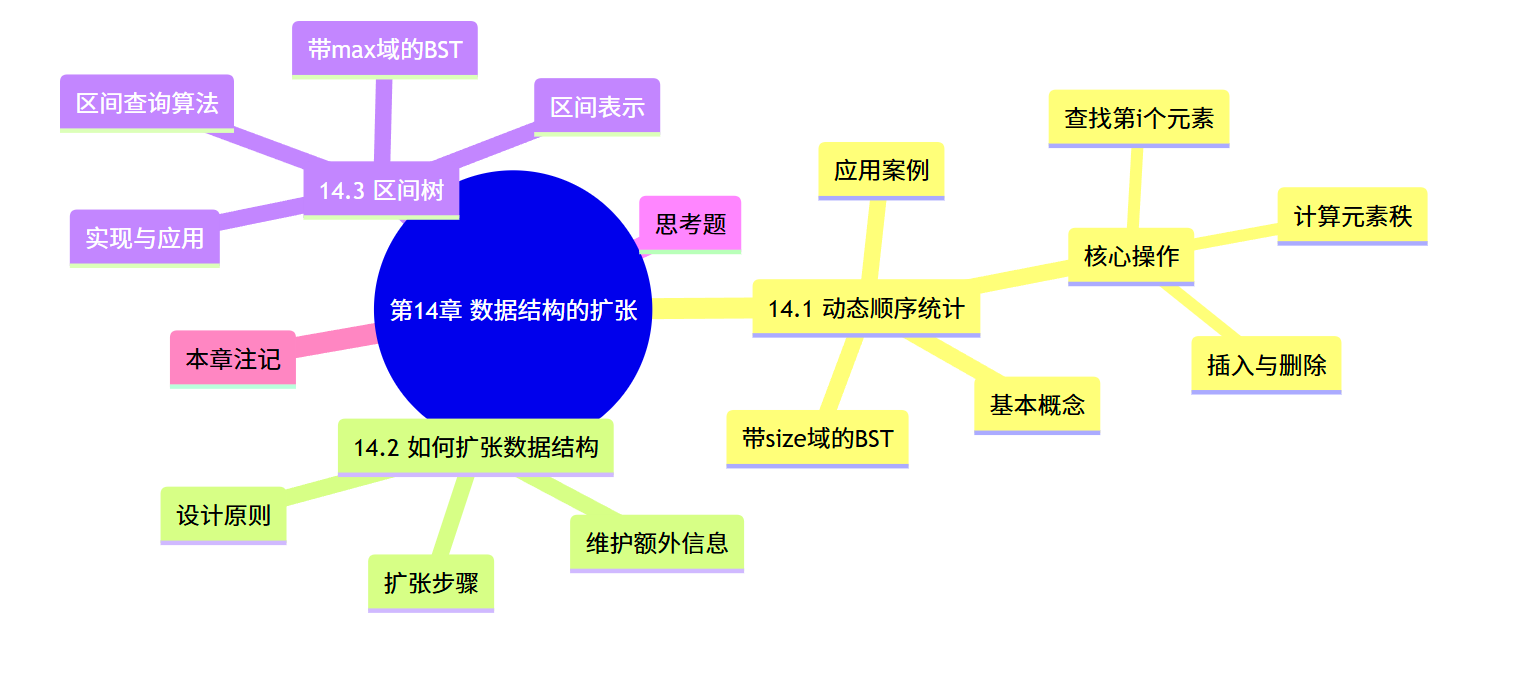
14.1 动态顺序统计

        在很多场景中，我们不仅需要像普通 BST 那样查找元素，还需要知道元素在集合中的排名（秩），或者查找集合中第 i 小的元素。动态顺序统计树就是为了解决这类问题而设计的。

基本概念

• 秩（Rank）：一个元素的秩是指该元素在集合的线性序中所处的位置（从 1 开始计数）
• 第 i 个顺序统计量：集合中第 i 小的元素

数据结构设计

        动态顺序统计树在普通 BST 的基础上，为每个节点增加了一个size属性，表示以该节点为根的子树中包含的节点总数（包括自身）。

// 动态顺序统计树节点结构struct Node { int key; // 节点关键字 int size; // 以该节点为根的子树大小 Node *left; // 左孩子 Node *right; // 右孩子 Node *parent; // 父节点 // 构造函数 Node(int k) : key(k), size(1), left(nullptr), right(nullptr), parent(nullptr) {}};

核心操作实现

更新节点大小

当树的结构发生变化（插入或删除节点）时，需要更新相关节点的size属性：

// 更新节点的size（等于左子树size + 右子树size + 1）void updateSize(Node *node) { if (node != nullptr) { node->size = 1; // 自身 if (node->left != nullptr) { node->size += node->left->size; } if (node->right != nullptr) { node->size += node->right->size; } }}

查找第 i 个元素

// 查找以node为根的子树中第i个最小元素（1-based）Node* select(Node *node, int i) { if (node == nullptr) return nullptr; // 空树或i超出范围 // 左子树的节点数 int leftSize = (node->left != nullptr) ? node->left->size : 0; if (i == leftSize + 1) { // 当前节点就是第i个元素 return node; } else if (i left, i); } else { // 第i个元素在右子树中，注意要调整i的值 return select(node->right, i - (leftSize + 1)); }}

计算元素的秩

// 计算x在以root为根的树中的秩int rank(Node *root, Node *x) { // x的左子树大小 + 1（自身） int r = (x->left != nullptr) ? x->left->size + 1 : 1; Node *y = x; // 向上追溯到根节点 while (y != root) { if (y == y->parent->right) { // 如果y是其父节点的右孩子，则需要加上父节点左子树大小 + 1（父节点自身） r += (y->parent->left != nullptr) ? y->parent->left->size + 1 : 1; } y = y->parent; } return r;}

插入操作

插入操作在普通 BST 插入的基础上，需要从新插入的节点向上更新所有祖先的size属性：

// 向以root为根的树中插入关键字key，返回新的根节点Node* insert(Node *root, int key) { // 普通BST插入逻辑 Node *parent = nullptr; Node **current = &root; while (*current != nullptr) { parent = *current; (*current)->size++; // 沿途节点size加1 if (key key) { current = &((*current)->left); } else { current = &((*current)->right); } } *current = new Node(key); (*current)->parent = parent; return root; // 返回新的根节点}

删除操作

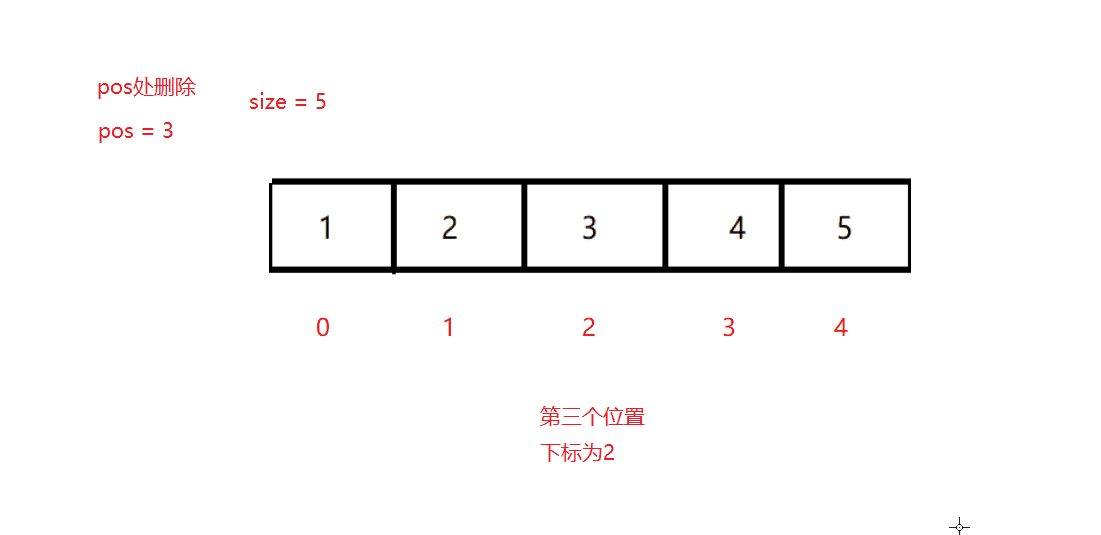
        删除操作相对复杂，需要先找到要删除的节点，执行删除（考虑三种情况：叶子节点、只有一个孩子、有两个孩子），然后更新相关节点的size属性：

// 查找关键字为key的节点Node* find(Node *root, int key) { Node *current = root; while (current != nullptr && current->key != key) { if (key key) { current = current->left; } else { current = current->right; } } return current;}// 找到以node为根的树中的最小值节点Node* minimum(Node *node) { while (node->left != nullptr) { node = node->left; } return node;}// 替换子树void transplant(Node *&root, Node *u, Node *v) { if (u->parent == nullptr) { root = v; // u是根节点 } else if (u == u->parent->left) { u->parent->left = v; // u是左孩子 } else { u->parent->right = v; // u是右孩子 } if (v != nullptr) { v->parent = u->parent; // 更新v的父节点 }}// 从树中删除节点z，返回新的根节点Node* deleteNode(Node *root, Node *z) { if (z == nullptr) return root; // 节点不存在 Node *y = nullptr; Node *x = nullptr; // 确定要删除的实际节点y if (z->left == nullptr || z->right == nullptr) { y = z; } else { y = minimum(z->right); // 找到后继节点 } // 确定y的孩子x if (y->left != nullptr) { x = y->left; } else { x = y->right; } // 更新x的父节点 if (x != nullptr) { x->parent = y->parent; } // 替换y transplant(root, y, x); // 如果y不是z，则将y的内容复制到z if (y != z) { z->key = y->key; } // 更新受影响节点的size Node *p = y->parent; while (p != nullptr) { updateSize(p); p = p->parent; } delete y; // 释放内存 return root;}

综合案例：动态顺序统计树的应用

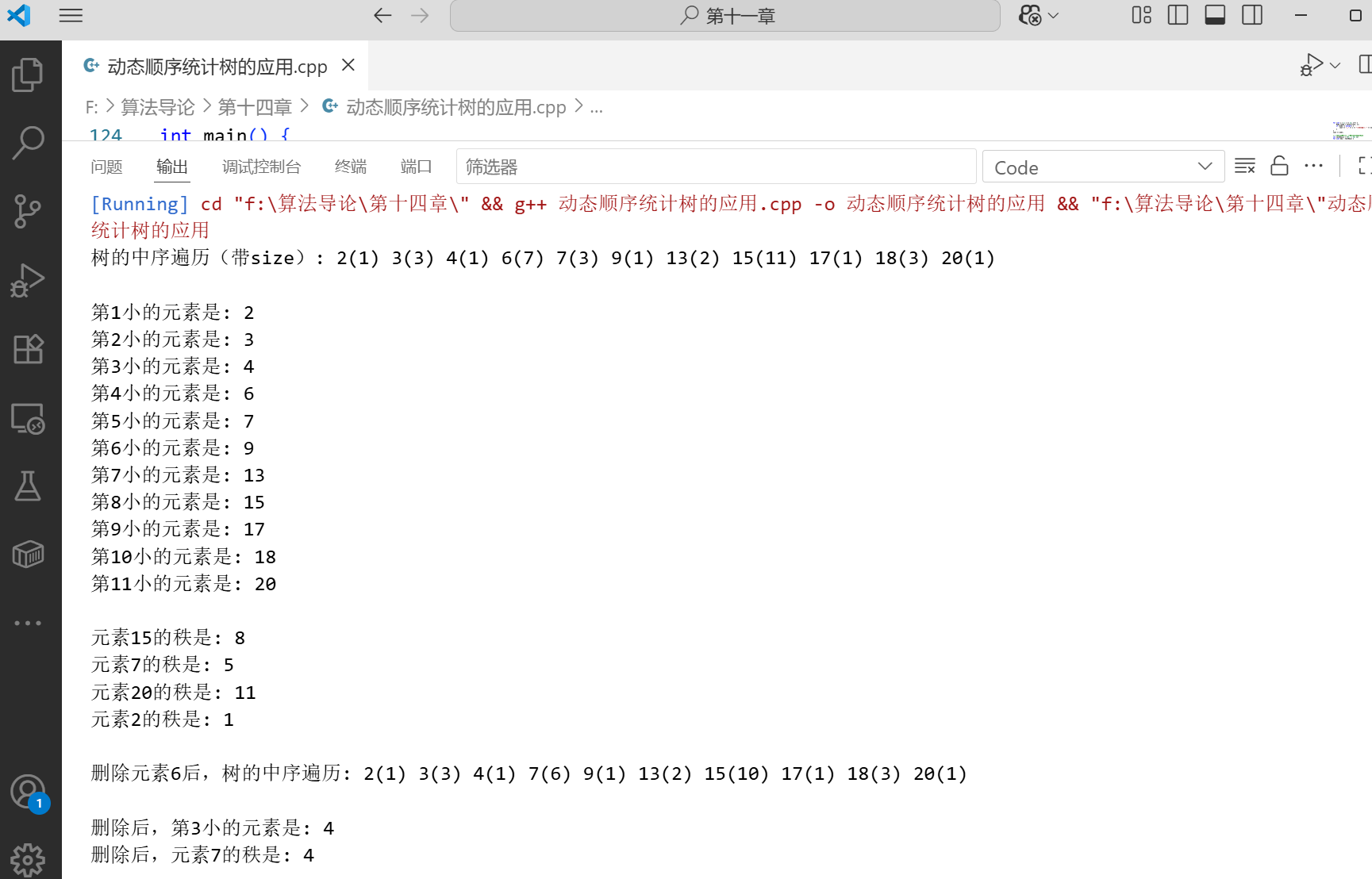
下面是一个完整的示例，展示了动态顺序统计树的各种操作：

#include #include using namespace std;// 节点结构定义struct Node { int key; int size; Node *left; Node *right; Node *parent; Node(int k) : key(k), size(1), left(nullptr), right(nullptr), parent(nullptr) {}};// 辅助函数声明void updateSize(Node *node);Node* select(Node *node, int i);int getRank(Node *root, Node *x); // 重命名rank为getRankNode* insert(Node *root, int key);Node* find(Node *root, int key);Node* minimum(Node *node);void transplant(Node *&root, Node *u, Node *v);Node* deleteNode(Node *root, Node *z);// 辅助函数实现void updateSize(Node *node) { if (node != nullptr) { node->size = 1; if (node->left != nullptr) node->size += node->left->size; if (node->right != nullptr) node->size += node->right->size; }}Node* select(Node *node, int i) { if (node == nullptr) return nullptr; int leftSize = (node->left != nullptr) ? node->left->size : 0; if (i == leftSize + 1) return node; else if (i left, i); else return select(node->right, i - (leftSize + 1));}// 重命名rank为getRank，避免与标准库冲突int getRank(Node *root, Node *x) { int r = (x->left != nullptr) ? x->left->size + 1 : 1; Node *y = x; while (y != root) { if (y == y->parent->right) { r += (y->parent->left != nullptr) ? y->parent->left->size + 1 : 1; } y = y->parent; } return r;}Node* insert(Node *root, int key) { Node *parent = nullptr; Node **current = &root; while (*current != nullptr) { parent = *current; (*current)->size++; if (key key) current = &((*current)->left); else current = &((*current)->right); } *current = new Node(key); (*current)->parent = parent; return root;}Node* find(Node *root, int key) { Node *current = root; while (current != nullptr && current->key != key) { if (key key) current = current->left; else current = current->right; } return current;}Node* minimum(Node *node) { while (node->left != nullptr) node = node->left; return node;}void transplant(Node *&root, Node *u, Node *v) { if (u->parent == nullptr) root = v; else if (u == u->parent->left) u->parent->left = v; else u->parent->right = v; if (v != nullptr) v->parent = u->parent;}Node* deleteNode(Node *root, Node *z) { if (z == nullptr) return root; Node *y = nullptr, *x = nullptr; if (z->left == nullptr || z->right == nullptr) y = z; else y = minimum(z->right); if (y->left != nullptr) x = y->left; else x = y->right; if (x != nullptr) x->parent = y->parent; transplant(root, y, x); if (y != z) z->key = y->key; Node *p = y->parent; while (p != nullptr) { updateSize(p); p = p->parent; } delete y; return root;}// 中序遍历打印树（用于调试）void inorder(Node *node) { if (node != nullptr) { inorder(node->left); cout <key << \"(\" <size <right); }}int main() { Node *root = nullptr; // 插入一些元素 int keys[] = {15, 6, 18, 3, 7, 17, 20, 2, 4, 13, 9}; for (int key : keys) { root = insert(root, key); } cout << \"树的中序遍历（带size）: \"; inorder(root); cout << endl << endl; // 测试select操作 for (int i = 1; i <= 11; i++) { Node *node = select(root, i); if (node != nullptr) { cout << \"第\" << i << \"小的元素是: \" <key << endl; } } cout << endl; // 测试rank操作，使用重命名后的getRank int testKeys[] = {15, 7, 20, 2}; for (int key : testKeys) { Node *node = find(root, key); if (node != nullptr) { cout << \"元素\" << key << \"的秩是: \" << getRank(root, node) << endl; } } cout << endl; // 测试删除操作 int delKey = 6; Node *delNode = find(root, delKey); if (delNode != nullptr) { cout << \"删除元素\" << delKey << \"后，树的中序遍历: \"; root = deleteNode(root, delNode); inorder(root); cout << endl << endl; // 再次测试select和rank操作 cout << \"删除后，第3小的元素是: \" <key << endl; cout << \"删除后，元素7的秩是: \" << getRank(root, find(root, 7)) << endl; } return 0;}

运行结果：

14.2 如何扩张数据结构

        扩张数据结构是指在现有数据结构的基础上添加新的信息和操作，以解决特定问题。以下是扩张数据结构的一般步骤：

1. 选择基础数据结构：通常选择能高效支持基本操作的数据结构（如 BST、红黑树等）

2. 确定要添加的信息：根据问题需求，确定需要在原有结构上添加哪些额外信息

3. 验证新信息可以被维护：确保在基础数据结构的所有操作（插入、删除等）执行后，新添加的信息仍能被正确维护

4. 实现新的操作：基于添加的信息，实现解决问题所需的新操作

设计原则

• 局部性：新信息应能通过节点本身及其子节点的信息计算得出
• 高效性：维护新信息的额外时间不应显著增加原有操作的时间复杂度
• 必要性：只添加解决问题所必需的信息，避免冗余

动态顺序统计树就是一个典型的扩张例子：

• 基础数据结构：二叉搜索树（BST）
• 添加的信息：每个节点的size属性
• 维护方式：插入 / 删除时更新路径上所有节点的size
• 新操作：select和rank

14.3 区间树

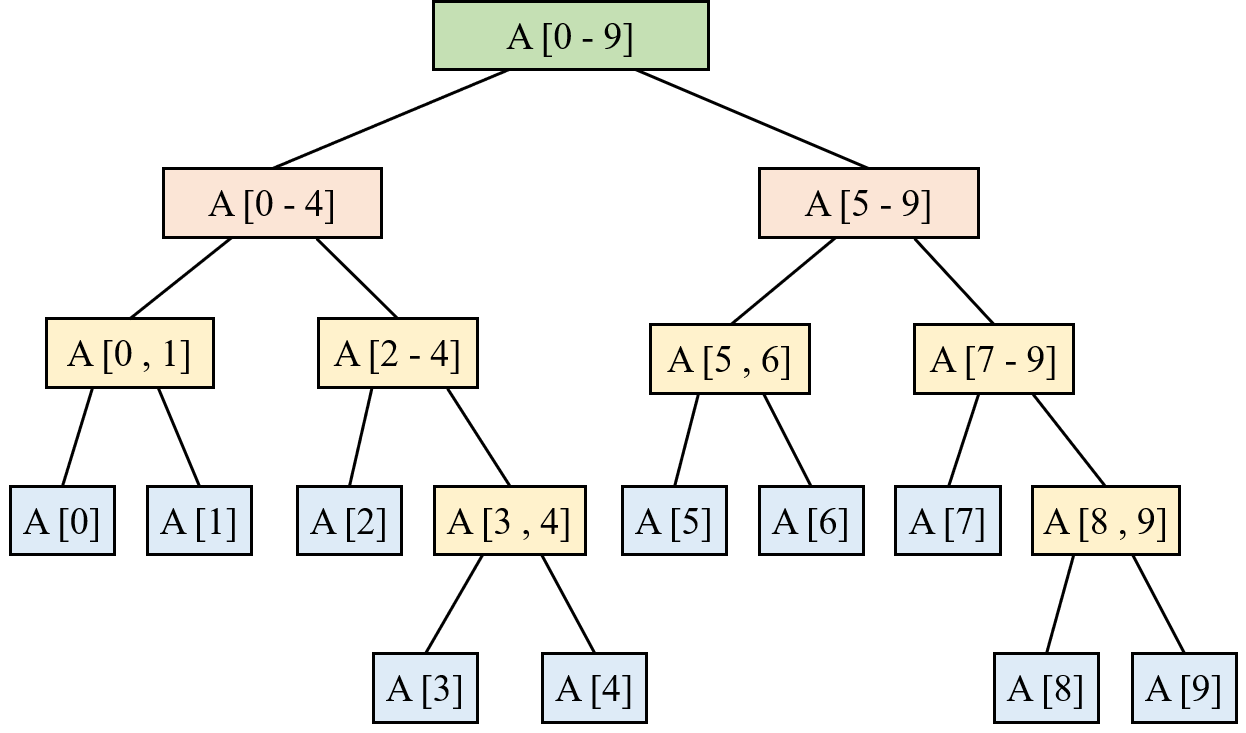
区间树是一种支持区间查询的数据结构，它能高效地找出与给定区间重叠的所有区间。

区间表示与问题定义

• 区间通常表示为[low, high]，其中low是区间的起点，high是区间的终点
• 两个区间[a,b]和[c,d]重叠当且仅当a ≤ d且c ≤ b
• 区间树的主要操作：插入区间、删除区间、查询所有与给定区间重叠的区间

数据结构设计

区间树基于 BST 扩展而来，每个节点存储：

• 一个区间[low, high]
• 以区间的low为关键字构建 BST
• 额外添加max属性，表示以该节点为根的子树中所有区间的high的最大值

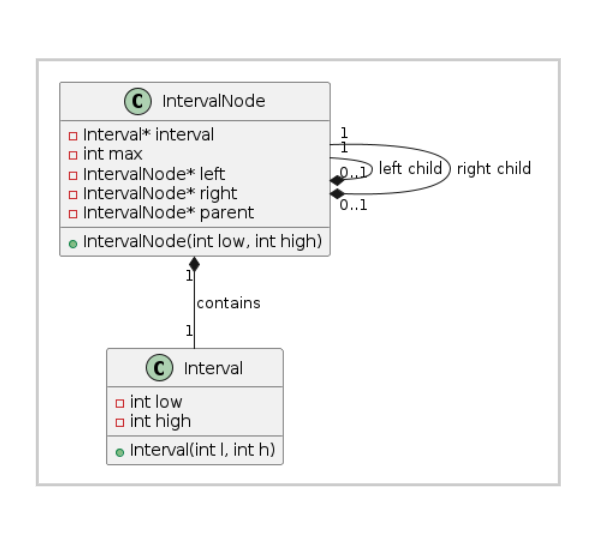
// 区间结构struct Interval { int low; // 区间起点 int high; // 区间终点 Interval(int l, int h) : low(l), high(h) {}};// 区间树节点结构struct IntervalNode { Interval *interval; // 区间 int max; // 子树中最大的high值 IntervalNode *left; // 左孩子 IntervalNode *right; // 右孩子 IntervalNode *parent;// 父节点 // 构造函数 IntervalNode(int low, int high) : interval(new Interval(low, high)), max(high), left(nullptr), right(nullptr), parent(nullptr) {}};

区间树的类图：

@startumlclass Interval { - int low - int high + Interval(int l, int h)}class IntervalNode { - Interval* interval - int max - IntervalNode* left - IntervalNode* right - IntervalNode* parent + IntervalNode(int low, int high)}IntervalNode \"1\" *-- \"1\" Interval : containsIntervalNode \"1\" --* \"0..1\" IntervalNode : left childIntervalNode \"1\" --* \"0..1\" IntervalNode : right child@enduml

核心操作实现

更新 max 值

// 更新节点的max值（自身high和左右子树max中的最大值）void updateMax(IntervalNode *node) { if (node != nullptr) { node->max = node->interval->high; // 自身区间的high if (node->left != nullptr && node->left->max > node->max) { node->max = node->left->max; } if (node->right != nullptr && node->right->max > node->max) { node->max = node->right->max; } }}

插入操作

// 向区间树中插入新区间IntervalNode* insertInterval(IntervalNode *root, int low, int high) { // 普通BST插入（以low为关键字） IntervalNode *parent = nullptr; IntervalNode **current = &root; while (*current != nullptr) { parent = *current; // 更新当前节点的max值 if (high > (*current)->max) { (*current)->max = high; } // 继续查找插入位置 if (low interval->low) { current = &((*current)->left); } else { current = &((*current)->right); } } // 创建新节点 *current = new IntervalNode(low, high); (*current)->parent = parent; return root;}

区间查询操作

查询所有与给定区间[low, high]重叠的区间：

// 检查两个区间是否重叠bool overlap(Interval *a, Interval *b) { return a->low high && b->low high;}// 查询与target重叠的所有区间void queryOverlapping(IntervalNode *node, Interval *target, vector& result) { if (node == nullptr) return; // 先检查左子树 if (node->left != nullptr && node->left->max >= target->low) { queryOverlapping(node->left, target, result); } // 检查当前节点 if (overlap(node->interval, target)) { result.push_back(node->interval); } // 再检查右子树 if (node->right != nullptr && node->interval->low high) { queryOverlapping(node->right, target, result); }}

查询算法的流程图：

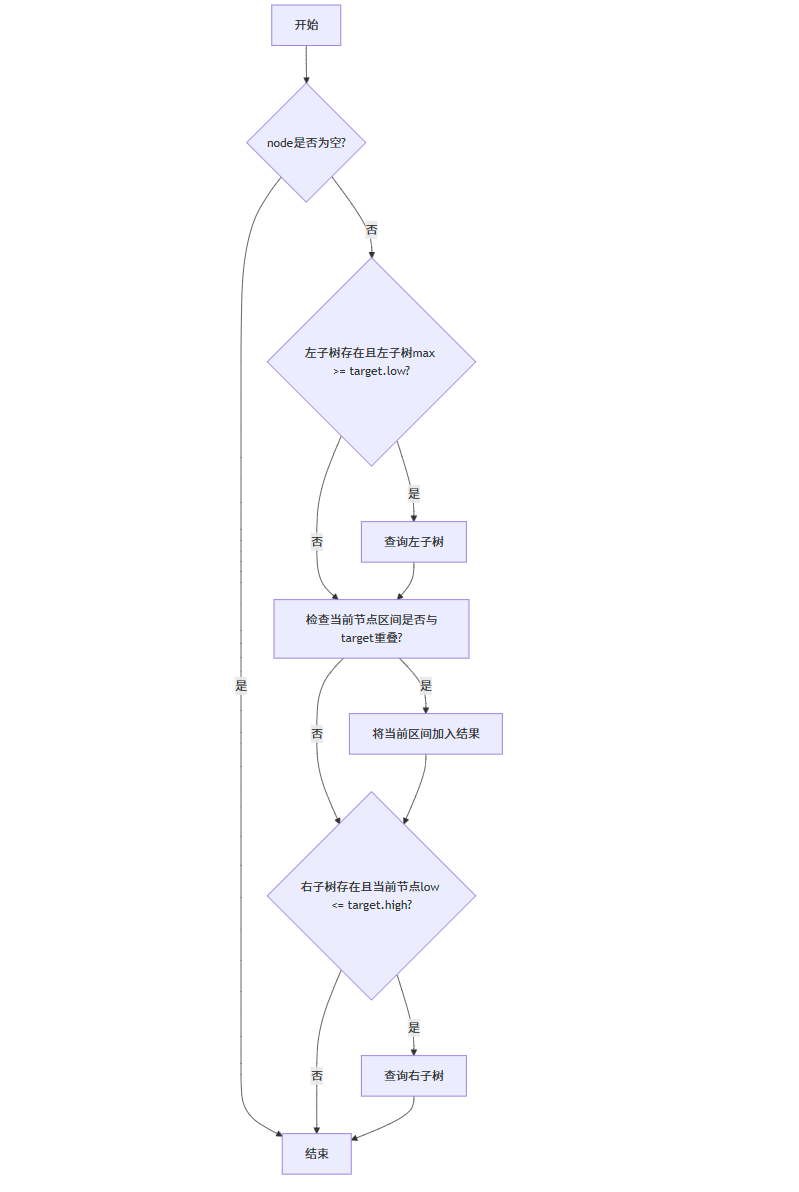
删除操作

删除操作需要在删除节点后更新相关节点的max值：

// 查找最小值节点（最左节点）IntervalNode* intervalMinimum(IntervalNode *node) { while (node->left != nullptr) { node = node->left; } return node;}// 区间树的替换操作void intervalTransplant(IntervalNode *&root, IntervalNode *u, IntervalNode *v) { if (u->parent == nullptr) { root = v; } else if (u == u->parent->left) { u->parent->left = v; } else { u->parent->right = v; } if (v != nullptr) { v->parent = u->parent; }}// 删除区间节点IntervalNode* deleteIntervalNode(IntervalNode *root, IntervalNode *z) { if (z == nullptr) return root; IntervalNode *y = nullptr; IntervalNode *x = nullptr; // 确定要删除的节点y if (z->left == nullptr || z->right == nullptr) { y = z; } else { y = intervalMinimum(z->right); } // 确定y的孩子x if (y->left != nullptr) { x = y->left; } else { x = y->right; } // 更新x的父节点 if (x != nullptr) { x->parent = y->parent; } // 替换y intervalTransplant(root, y, x); // 如果y不是z，则复制y的内容到z if (y != z) { // 保存z的区间指针以便后续释放 Interval *oldInterval = z->interval; // 复制y的内容到z z->interval = y->interval; z->max = y->max; // 释放y的区间（因为已经转移给z了） y->interval = nullptr; delete oldInterval; } // 更新受影响节点的max值 IntervalNode *p = y->parent; while (p != nullptr) { updateMax(p); p = p->parent; } // 释放y的内存 if (y->interval != nullptr) { delete y->interval; } delete y; return root;}// 查找包含特定区间的节点IntervalNode* findIntervalNode(IntervalNode *root, int low, int high) { IntervalNode *current = root; while (current != nullptr) { if (current->interval->low == low && current->interval->high == high) { return current; } else if (low interval->low) { current = current->left; } else { current = current->right; } } return nullptr;}

综合案例：区间树的应用

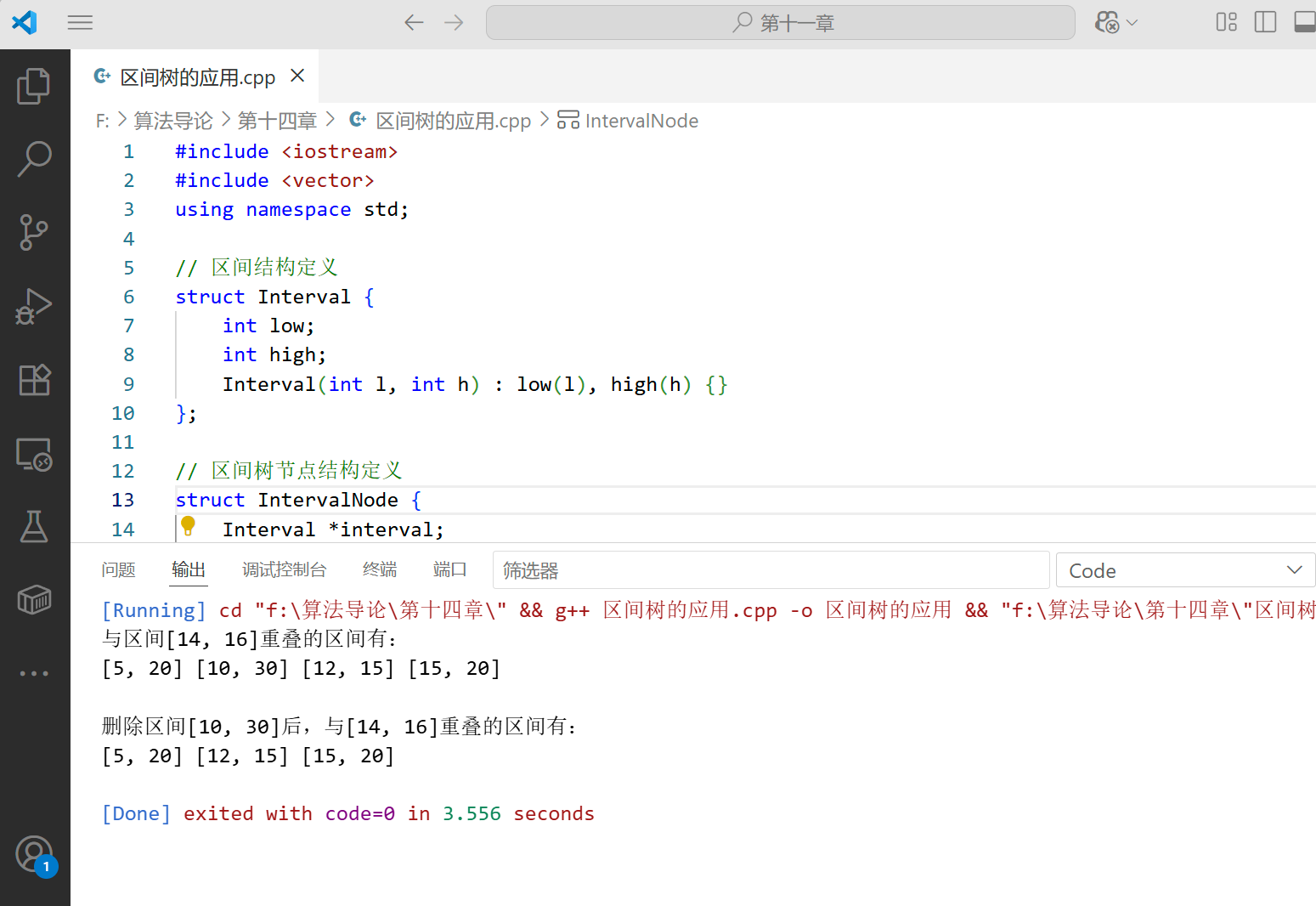
下面是一个完整的区间树应用示例：

#include #include using namespace std;// 区间结构定义struct Interval { int low; int high; Interval(int l, int h) : low(l), high(h) {}};// 区间树节点结构定义struct IntervalNode { Interval *interval; int max; IntervalNode *left; IntervalNode *right; IntervalNode *parent; IntervalNode(int low, int high) : interval(new Interval(low, high)), max(high), left(nullptr), right(nullptr), parent(nullptr) {}};// 辅助函数声明void updateMax(IntervalNode *node);IntervalNode* insertInterval(IntervalNode *root, int low, int high);bool overlap(Interval *a, Interval *b);void queryOverlapping(IntervalNode *node, Interval *target, vector& result);IntervalNode* intervalMinimum(IntervalNode *node);void intervalTransplant(IntervalNode *&root, IntervalNode *u, IntervalNode *v);IntervalNode* deleteIntervalNode(IntervalNode *root, IntervalNode *z);IntervalNode* findIntervalNode(IntervalNode *root, int low, int high);// 辅助函数实现void updateMax(IntervalNode *node) { if (node != nullptr) { node->max = node->interval->high; if (node->left != nullptr && node->left->max > node->max) { node->max = node->left->max; } if (node->right != nullptr && node->right->max > node->max) { node->max = node->right->max; } }}IntervalNode* insertInterval(IntervalNode *root, int low, int high) { IntervalNode *parent = nullptr; IntervalNode **current = &root; while (*current != nullptr) { parent = *current; if (high > (*current)->max) { (*current)->max = high; } if (low interval->low) { current = &((*current)->left); } else { current = &((*current)->right); } } *current = new IntervalNode(low, high); (*current)->parent = parent; return root;}bool overlap(Interval *a, Interval *b) { return a->low high && b->low high;}void queryOverlapping(IntervalNode *node, Interval *target, vector& result) { if (node == nullptr) return; if (node->left != nullptr && node->left->max >= target->low) { queryOverlapping(node->left, target, result); } if (overlap(node->interval, target)) { result.push_back(node->interval); } if (node->right != nullptr && node->interval->low high) { queryOverlapping(node->right, target, result); }}IntervalNode* intervalMinimum(IntervalNode *node) { while (node->left != nullptr) { node = node->left; } return node;}void intervalTransplant(IntervalNode *&root, IntervalNode *u, IntervalNode *v) { if (u->parent == nullptr) { root = v; } else if (u == u->parent->left) { u->parent->left = v; } else { u->parent->right = v; } if (v != nullptr) { v->parent = u->parent; }}IntervalNode* deleteIntervalNode(IntervalNode *root, IntervalNode *z) { if (z == nullptr) return root; IntervalNode *y = nullptr; IntervalNode *x = nullptr; if (z->left == nullptr || z->right == nullptr) { y = z; } else { y = intervalMinimum(z->right); } if (y->left != nullptr) { x = y->left; } else { x = y->right; } if (x != nullptr) { x->parent = y->parent; } intervalTransplant(root, y, x); if (y != z) { Interval *oldInterval = z->interval; z->interval = y->interval; z->max = y->max; y->interval = nullptr; delete oldInterval; } IntervalNode *p = y->parent; while (p != nullptr) { updateMax(p); p = p->parent; } if (y->interval != nullptr) { delete y->interval; } delete y; return root;}IntervalNode* findIntervalNode(IntervalNode *root, int low, int high) { IntervalNode *current = root; while (current != nullptr) { if (current->interval->low == low && current->interval->high == high) { return current; } else if (low interval->low) { current = current->left; } else { current = current->right; } } return nullptr;}// 打印区间void printInterval(Interval *interval) { cout << \"[\" <low << \", \" <high << \"]\";}int main() { IntervalNode *root = nullptr; // 插入一些区间 root = insertInterval(root, 15, 20); root = insertInterval(root, 10, 30); root = insertInterval(root, 17, 19); root = insertInterval(root, 5, 20); root = insertInterval(root, 12, 15); root = insertInterval(root, 30, 40); // 查询与[14, 16]重叠的区间 Interval *target = new Interval(14, 16); vector result; queryOverlapping(root, target, result); cout << \"与区间[14, 16]重叠的区间有：\" << endl; for (Interval *interval : result) { printInterval(interval); cout << \" \"; } cout << endl << endl; // 删除区间[10, 30] IntervalNode *nodeToDelete = findIntervalNode(root, 10, 30); if (nodeToDelete != nullptr) { root = deleteIntervalNode(root, nodeToDelete); cout << \"删除区间[10, 30]后，与[14, 16]重叠的区间有：\" << endl; result.clear(); queryOverlapping(root, target, result); for (Interval *interval : result) { printInterval(interval); cout << \" \"; } cout << endl; } // 释放内存 delete target; // 完整的内存释放还需要遍历树删除所有节点，这里简化处理 return 0;}

运行结果：

思考题

1. 如何在动态顺序统计树上实现范围查询（即查找所有关键字在 [a, b] 之间的元素），并计算该范围内元素的个数？

2. 试设计一种基于红黑树的区间树，确保所有操作（插入、删除、查询）都能在 O (log n) 时间内完成。

3. 如何扩展区间树，使其能高效支持 “查找包含点 x 的所有区间” 这一操作？

4. 设计一种数据结构，支持在 O (1) 时间内查找最小值，在 O (log n) 时间内插入和删除元素，以及在 O (log n) 时间内查找第 i 小的元素。

本章注记

• 数据结构的扩张是解决复杂问题的重要技术，其核心在于找到合适的基础结构和需要添加的信息
• 红黑树常被用作扩张的基础结构，因为它能在 O (log n) 时间内支持插入、删除等操作
• 除了本章介绍的动态顺序统计树和区间树，还有许多其他重要的扩张数据结构，如：
  • 线段树：用于处理区间上的范围查询和更新
  • 二叉索引树（Fenwick 树）：高效支持前缀和查询和点更新
  • 平衡二叉搜索树：如 AVL 树、Splay 树等，在 BST 基础上添加了平衡条件

        希望本章内容能帮助大家理解数据结构扩张的思想和方法。通过动手实现这些数据结构，相信大家能更深入地掌握其中的原理和技巧。如果有任何疑问或建议，欢迎在评论区留言讨论！