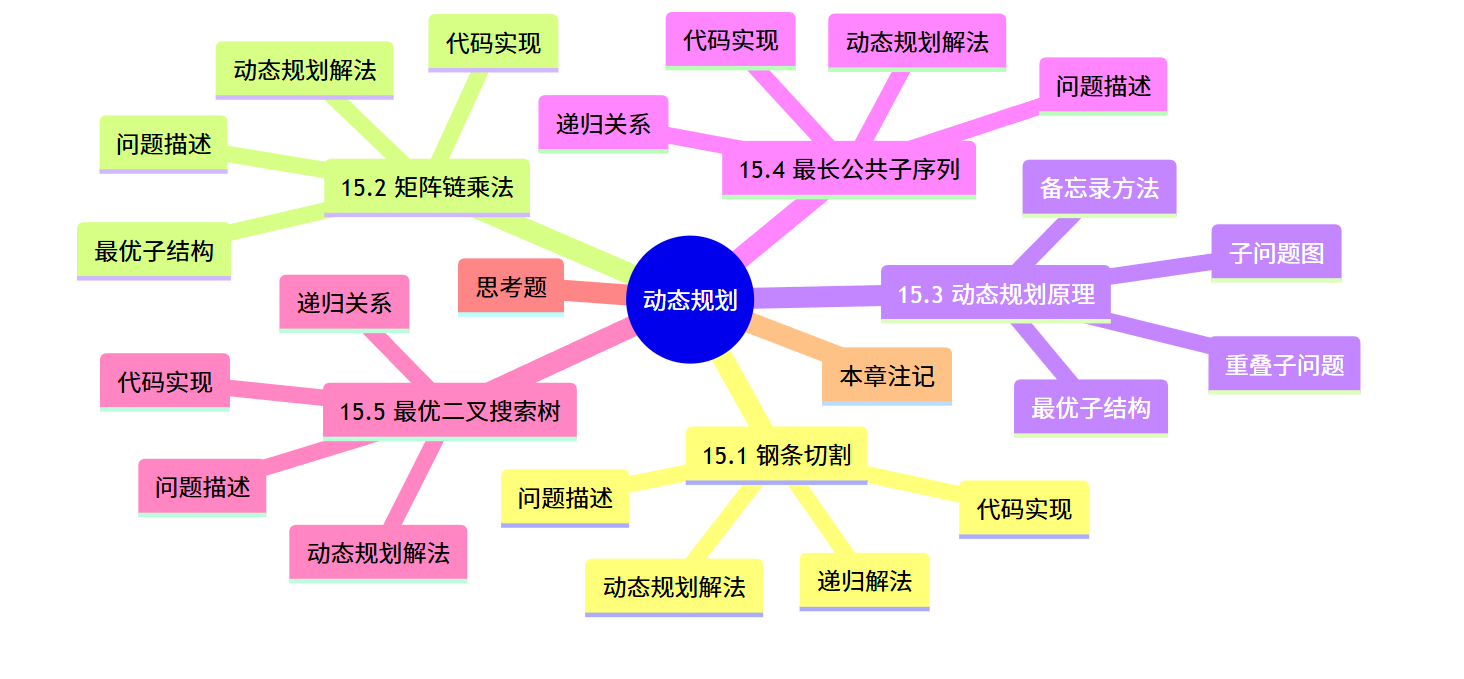
《算法导论》第 15 章 - 动态规划
大家好,今天我们来深入探讨《算法导论》中非常重要的一章 —— 动态规划(Dynamic Programming)。动态规划是一种通过将复杂问题分解为重叠子问题,并利用子问题的解来构建原问题解的高效算法设计技术。在很多优化问题中,动态规划都能发挥巨大作用。
15.1 钢条切割

问题描述
钢条切割问题是动态规划中的一个经典入门问题:
- 给定一段长度为 n 的钢条
- 已知长度为 i 的钢条的售价为 p_i(i=1,2,...,n)
- 我们需要将钢条切割成若干段,使得总售价最大化
解法思路
-
递归方法:对于长度为 n 的钢条,第一次切割后可以得到长度为 i 和 n-i 的两段,其中 i=1,2,...,n。则最大收益 r (n) = max (p_i + r (n-i)),其中 i=1,2,...,n。
-
动态规划方法:递归方法存在大量重复计算,动态规划通过存储子问题的解来避免重复计算,有两种实现方式:
- 自顶向下(带备忘录)
- 自底向上
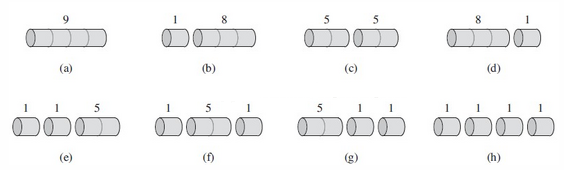
完整代码实现
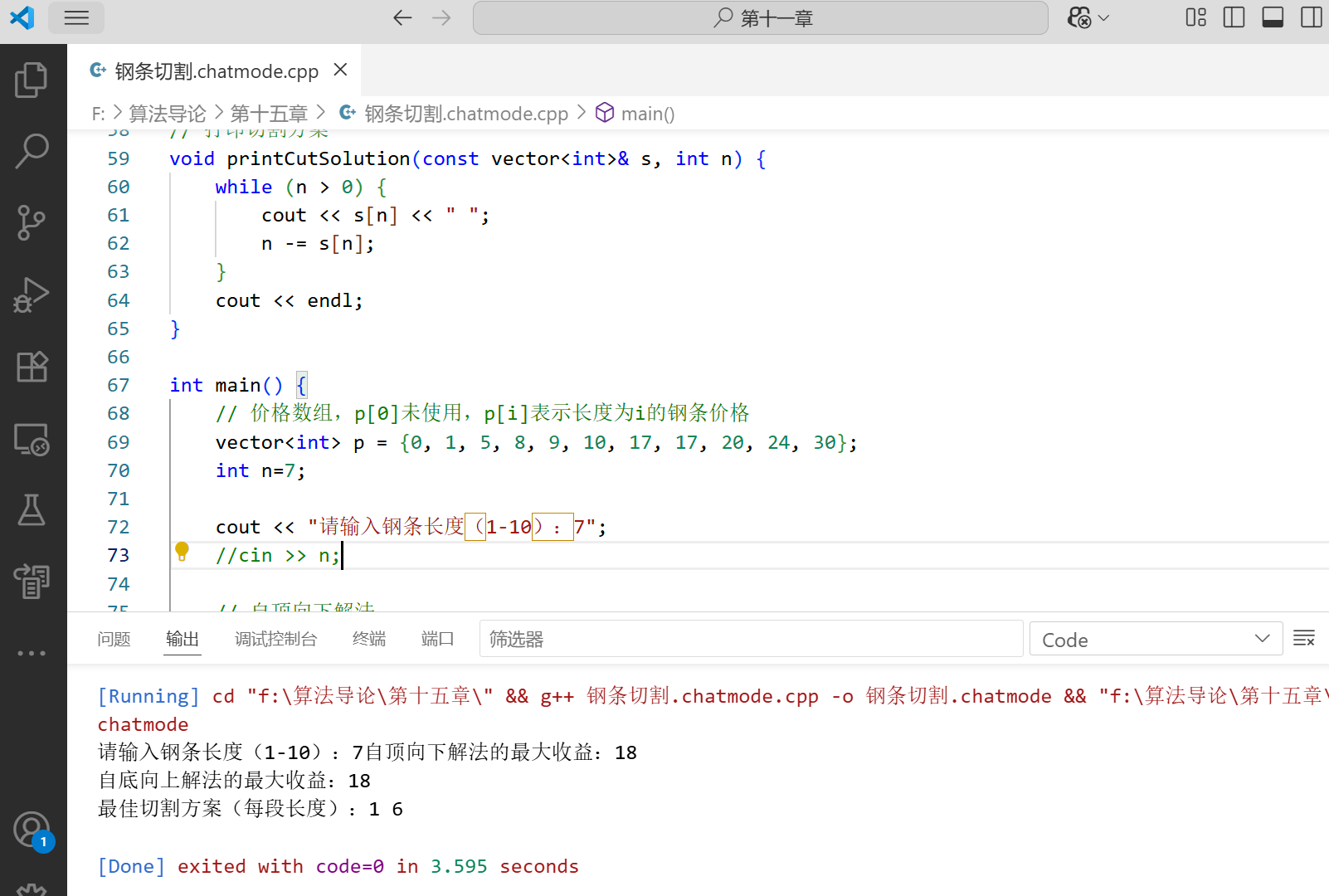
#include #include #include #include using namespace std;// 自顶向下的动态规划解法(带备忘录)int cutRodMemoized(const vector& p, int n, vector& memo) { // 如果已经计算过,直接返回 if (memo[n] >= 0) { return memo[n]; } int q; // 基本情况:长度为0的钢条收益为0 if (n == 0) { q = 0; } else { q = INT_MIN; // 尝试所有可能的切割 for (int i = 1; i <= n; ++i) { q = max(q, p[i] + cutRodMemoized(p, n - i, memo)); } } // 存储计算结果 memo[n] = q; return q;}int memoizedCutRod(const vector& p, int n) { // 初始化备忘录数组,所有值设为-∞ vector memo(n + 1, INT_MIN); return cutRodMemoized(p, n, memo);}// 自底向上的动态规划解法int bottomUpCutRod(const vector& p, int n, vector& s) { // dp[i]表示长度为i的钢条的最大收益 vector dp(n + 1, 0); // 计算长度为i的钢条的最大收益 for (int i = 1; i <= n; ++i) { int q = INT_MIN; // 尝试所有可能的切割 for (int j = 1; j <= i; ++j) { if (q < p[j] + dp[i - j]) { q = p[j] + dp[i - j]; s[i] = j; // 记录最佳切割点 } } dp[i] = q; } return dp[n];}// 打印切割方案void printCutSolution(const vector& s, int n) { while (n > 0) { cout << s[n] << \" \"; n -= s[n]; } cout << endl;}int main() { // 价格数组,p[0]未使用,p[i]表示长度为i的钢条价格 vector p = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30}; int n; cout <> n; // 自顶向下解法 int maxPriceMemo = memoizedCutRod(p, n); cout << \"自顶向下解法的最大收益:\" << maxPriceMemo << endl; // 自底向上解法 vector s(n + 1, 0); // 存储切割方案 int maxPriceBottomUp = bottomUpCutRod(p, n, s); cout << \"自底向上解法的最大收益:\" << maxPriceBottomUp << endl; cout << \"最佳切割方案(每段长度):\"; printCutSolution(s, n); return 0;}代码说明
-
自顶向下解法:
- 使用备忘录(memo 数组)存储已经计算过的子问题结果
- 递归地将问题分解为更小的子问题
- 当需要解决一个子问题时,先检查是否已经计算过,如果是则直接返回结果
-
自底向上解法:
- 从最小的子问题开始(长度为 1 的钢条),逐步计算更大的子问题
- 使用 dp 数组存储每个长度的最大收益
- 使用 s 数组记录每个长度的最佳切割点,以便后续重构切割方案
-
切割方案打印:
- 根据 s 数组,从长度 n 开始,每次输出最佳切割长度,然后处理剩余长度
应用场景
钢条切割问题是资源分配问题的一个简化模型,类似的问题在实际中有很多应用:
- 木材切割:如何切割木材获得最大收益
- 布料裁剪:如何裁剪布料使利用率最高
- 时间分配:如何分配时间到不同任务以获得最大效率

15.2 矩阵链乘法
问题描述
矩阵链乘法问题研究的是如何确定矩阵相乘的顺序,以最小化总的标量乘法次数:
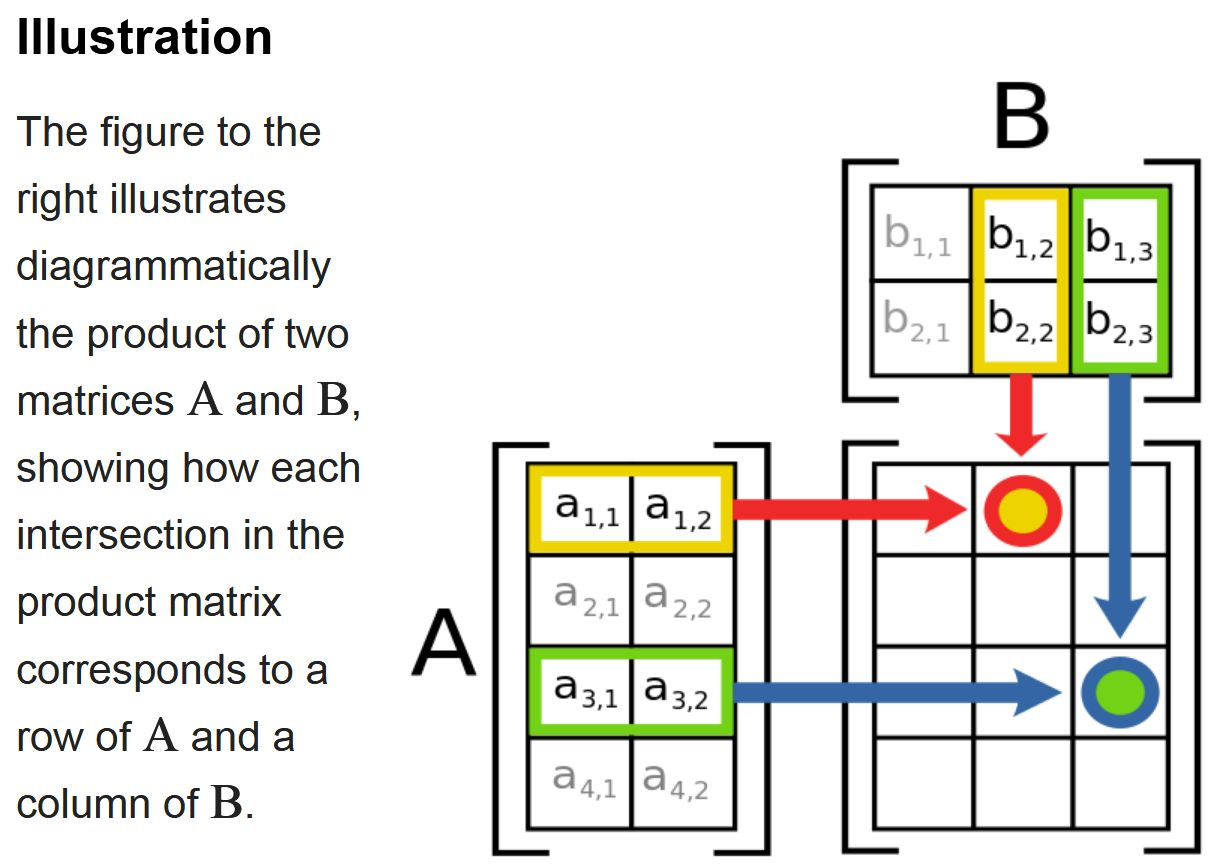
- 给定 n 个矩阵的链 A₁, A₂, ..., Aₙ,其中 Aᵢ是 pᵢ₋₁×pᵢ的矩阵
- 矩阵乘法满足结合律,不同的相乘顺序会导致不同的计算量
- 我们需要找到一种相乘顺序,使得总的标量乘法次数最少
例如,对于 3 个矩阵 A₁(10×100)、A₂(100×5)、A₃(5×50):
- (A₁A₂) A₃:需要 10×100×5 + 10×5×50 = 5000 + 2500 = 7500 次乘法
- A₁(A₂A₃):需要 100×5×50 + 10×100×50 = 25000 + 50000 = 75000 次乘法
可见,不同的计算顺序会导致计算量的巨大差异。
解法思路
-
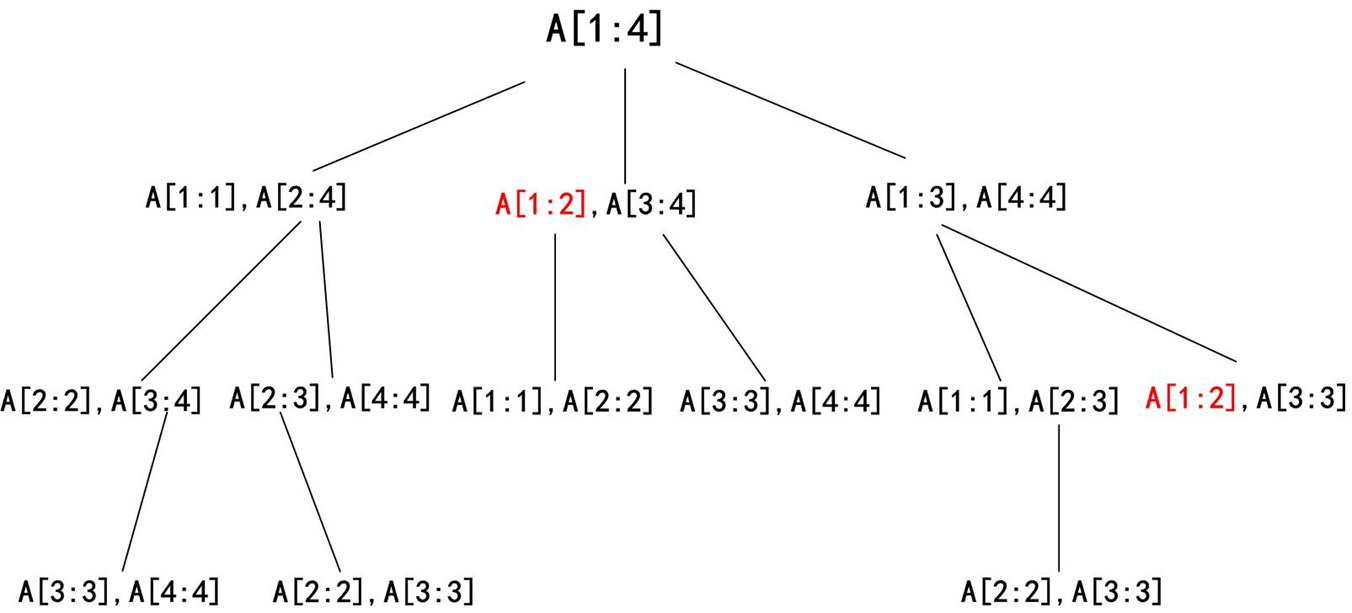
最优子结构:设 Aᵢ...Aⱼ表示矩阵 Aᵢ到 Aⱼ的乘积,若在 Aₖ处拆分,则:
- 最优解 cost (i,j) = cost (i,k) + cost (k+1,j) + pᵢ₋₁×pₖ×pⱼ
- 我们需要找到 k (i≤k<j) 使得 cost (i,j) 最小
-
动态规划解法:
- 定义 dp [i][j] 为计算矩阵 Aᵢ...Aⱼ所需的最小标量乘法次数
- 定义 s [i][j] 为矩阵 Aᵢ...Aⱼ的最优拆分点 k
完整代码实现
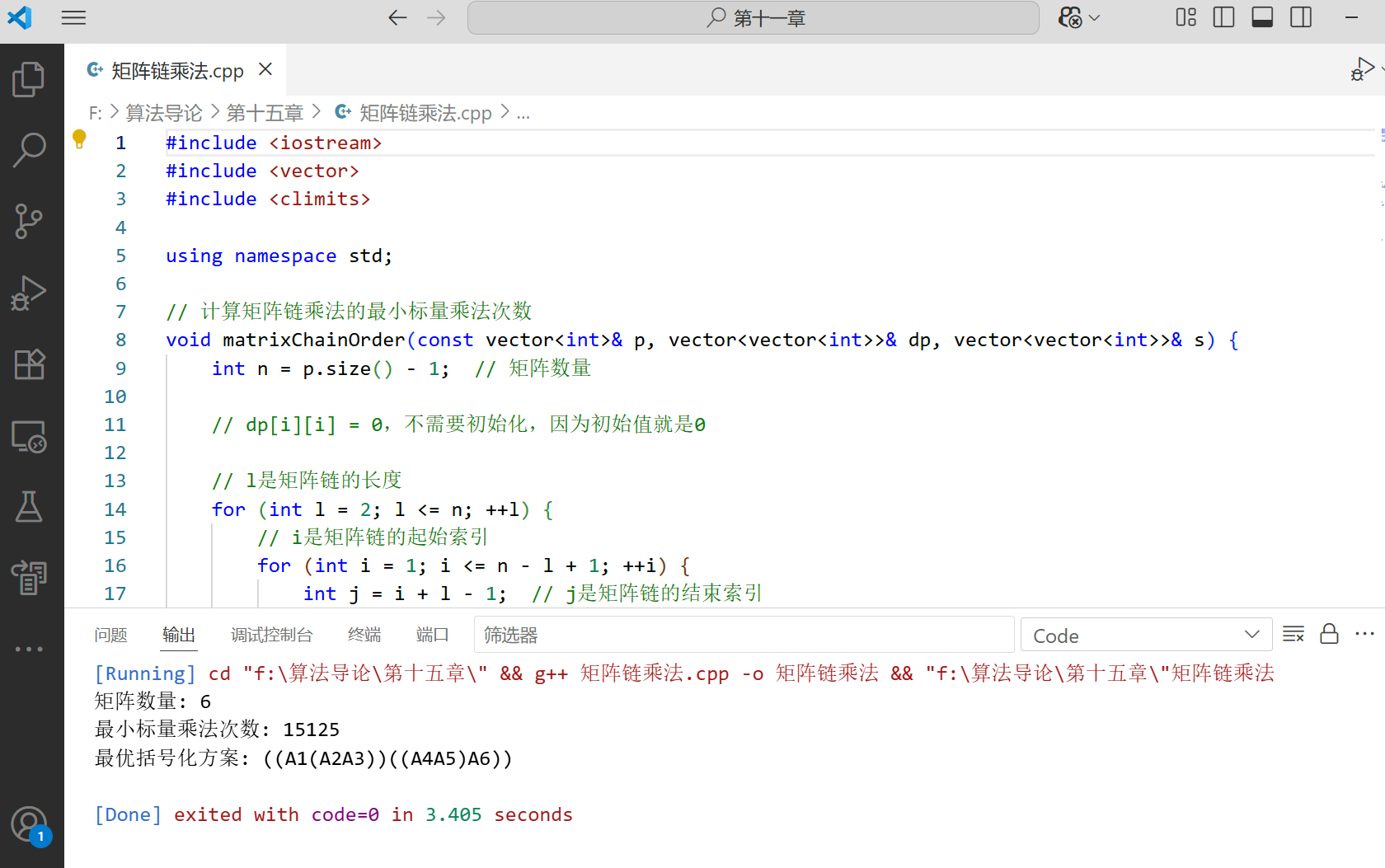
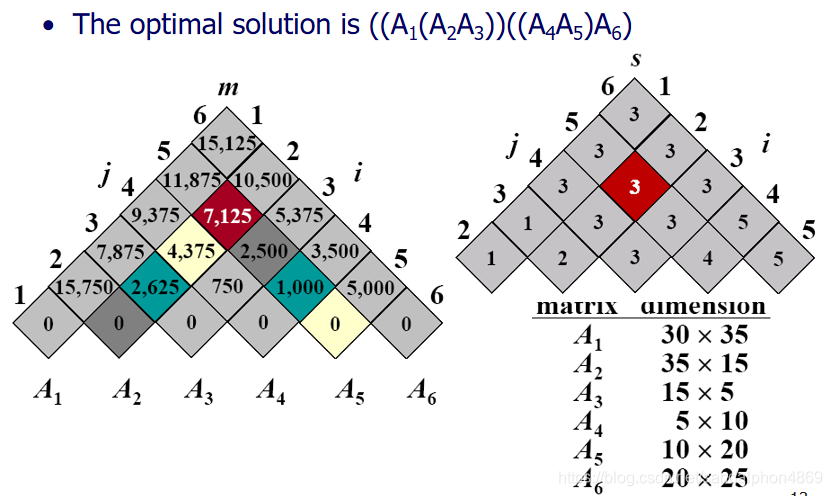
#include #include #include using namespace std;// 计算矩阵链乘法的最小标量乘法次数void matrixChainOrder(const vector& p, vector<vector>& dp, vector<vector>& s) { int n = p.size() - 1; // 矩阵数量 // dp[i][i] = 0,不需要初始化,因为初始值就是0 // l是矩阵链的长度 for (int l = 2; l <= n; ++l) { // i是矩阵链的起始索引 for (int i = 1; i <= n - l + 1; ++i) { int j = i + l - 1; // j是矩阵链的结束索引 dp[i][j] = INT_MAX; // 尝试所有可能的拆分点k for (int k = i; k < j; ++k) { // 计算当前拆分的代价 int q = dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] * p[j]; // 如果当前代价更小,则更新 if (q < dp[i][j]) { dp[i][j] = q; s[i][j] = k; // 记录最佳拆分点 } } } }}// 打印最优括号化方案void printOptimalParens(const vector<vector>& s, int i, int j) { if (i == j) { cout << \"A\" << i; } else { cout << \"(\"; printOptimalParens(s, i, s[i][j]); printOptimalParens(s, s[i][j] + 1, j); cout << \")\"; }}int main() { // 矩阵维度数组,p[0..n],其中A_i是p[i-1]×p[i]的矩阵 vector p = {30, 35, 15, 5, 10, 20, 25}; int n = p.size() - 1; // 矩阵数量 // dp[i][j]表示计算A_i到A_j所需的最小标量乘法次数 vector<vector> dp(n + 1, vector(n + 1, 0)); // s[i][j]表示A_i到A_j的最优拆分点 vector<vector> s(n + 1, vector(n + 1, 0)); // 计算最优解 matrixChainOrder(p, dp, s); // 输出结果 cout << \"矩阵数量: \" << n << endl; cout << \"最小标量乘法次数: \" << dp[1][n] << endl; cout << \"最优括号化方案: \"; printOptimalParens(s, 1, n); cout << endl; return 0;}代码说明
-
matrixChainOrder 函数:
- 输入:矩阵维度数组 p,dp 数组和 s 数组
- 功能:填充 dp 数组和 s 数组,计算最小标量乘法次数和最优拆分点
- 实现:按照矩阵链长度递增的顺序计算,对于每个长度为 l 的矩阵链,尝试所有可能的起始位置 i 和拆分点 k
-
printOptimalParens 函数:
- 输入:s 数组,起始索引 i 和结束索引 j
- 功能:递归地打印矩阵链 Aᵢ到 Aⱼ的最优括号化方案
- 实现:根据 s [i][j] 找到最优拆分点,递归打印左右两部分
-
主函数:
- 定义矩阵维度数组 p
- 初始化 dp 和 s 数组
- 调用 matrixChainOrder 计算最优解
- 输出最小标量乘法次数和最优括号化方案
应用场景
矩阵链乘法问题是优化问题中的一个经典案例,其思想可以应用于:
- 编译器优化:表达式求值顺序优化
- 数据库查询优化:多表连接顺序优化
- 信号处理:矩阵运算顺序优化
15.3 动态规划原理
动态规划是一种求解复杂问题的高效方法,它的核心思想是将复杂问题分解为重叠子问题,并利用子问题的解来构建原问题的解。动态规划方法通常比朴素的递归方法效率更高,因为它避免了重复计算。
最优子结构
如果一个问题的最优解包含其子问题的最优解,那么该问题具有最优子结构性质。这是动态规划能够应用的基础。
在钢条切割问题中,长度为 n 的钢条的最优切割方案包含了长度为 k(k < n)的钢条的最优切割方案。
在矩阵链乘法问题中,矩阵链 Aᵢ...Aⱼ的最优计算方案包含了子链 Aᵢ...Aₖ和 Aₖ₊₁...Aⱼ的最优计算方案。
如何利用最优子结构:
- 证明问题的最优解包含子问题的最优解
- 递归地定义最优解的值
- 计算最优解的值(自底向上或自顶向下带备忘录)
重叠子问题
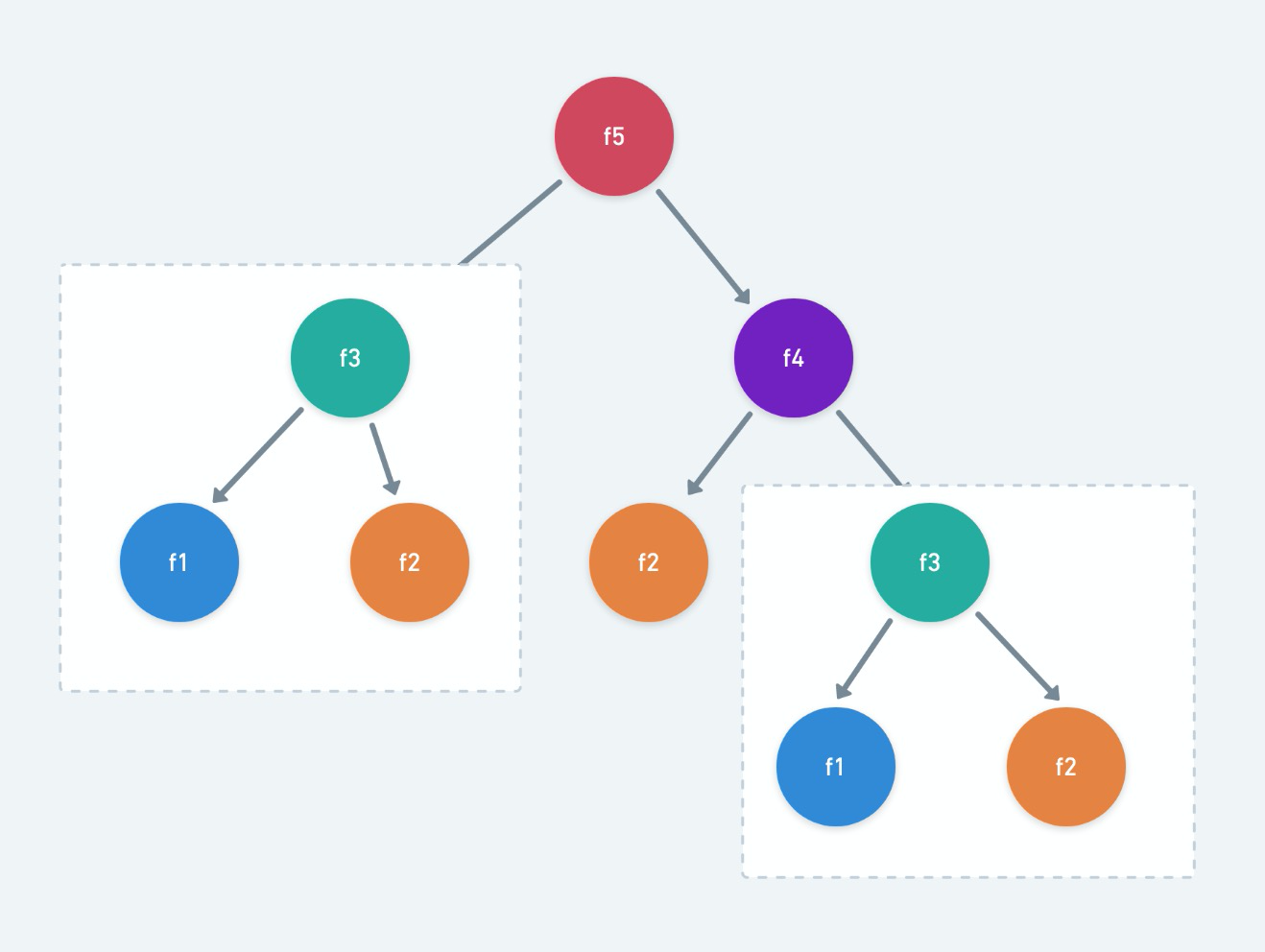
如果一个问题可以分解为若干个子问题,且这些子问题会被重复计算多次,那么该问题具有重叠子问题性质。动态规划通过存储子问题的解来避免重复计算,从而提高效率。
例如,在钢条切割问题中,计算 r (4) 时需要计算 r (3)、r (2)、r (1),而计算 r (5) 时又需要再次计算这些值。
动态规划处理重叠子问题的两种方式:
- 自顶向下带备忘录:递归计算,同时存储子问题的解
- 自底向上:按照子问题规模递增的顺序计算,存储子问题的解
子问题图
子问题图可以帮助我们可视化动态规划问题的结构:
- 每个节点代表一个子问题
- 每条边代表子问题之间的依赖关系
子问题图的规模(节点数)决定了动态规划算法的时间复杂度的下界。
备忘录方法
备忘录方法是自顶向下动态规划的实现方式:
- 使用一个表格(数组或哈希表)存储已经计算过的子问题的解
- 当需要计算一个子问题时,首先检查表格中是否已经存在该子问题的解
- 如果存在,则直接返回
- 如果不存在,则计算并存储在表格中
备忘录方法结合了递归的简洁性和动态规划的高效性,是一种非常实用的技术。
15.4 最长公共子序列
问题描述
最长公共子序列(LCS)问题是字符串处理中的一个经典问题:
- 给定两个字符串 X 和 Y
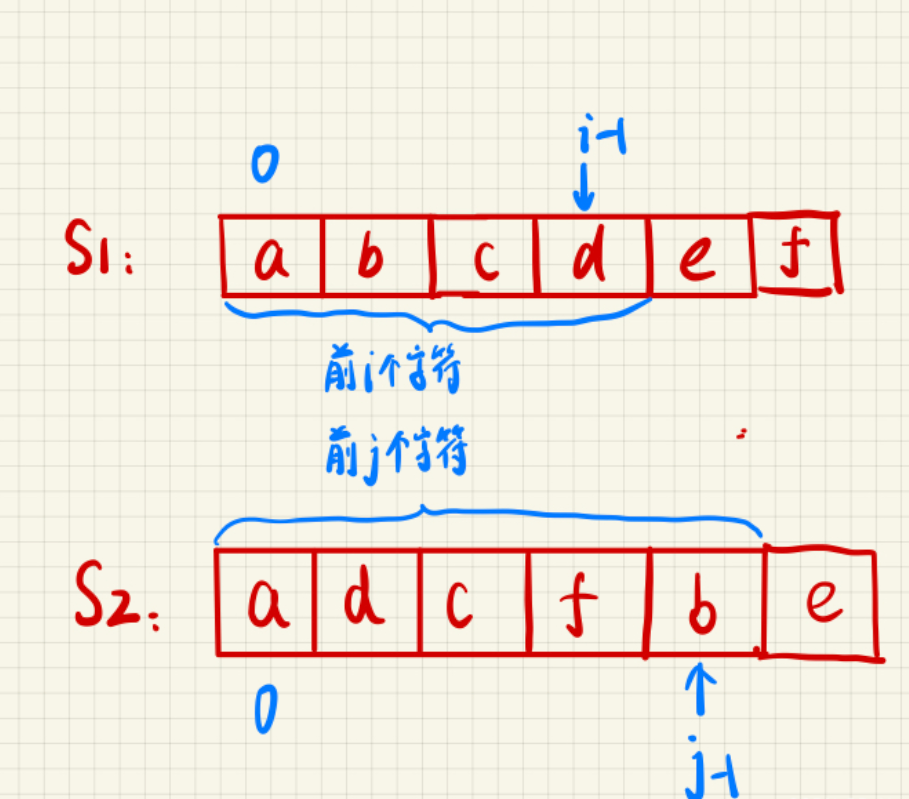
- 子序列是指从一个字符串中删除若干个字符(可以不删除)后,保持剩余字符相对顺序不变得到的字符串
- 最长公共子序列是指两个字符串中长度最长的公共子序列
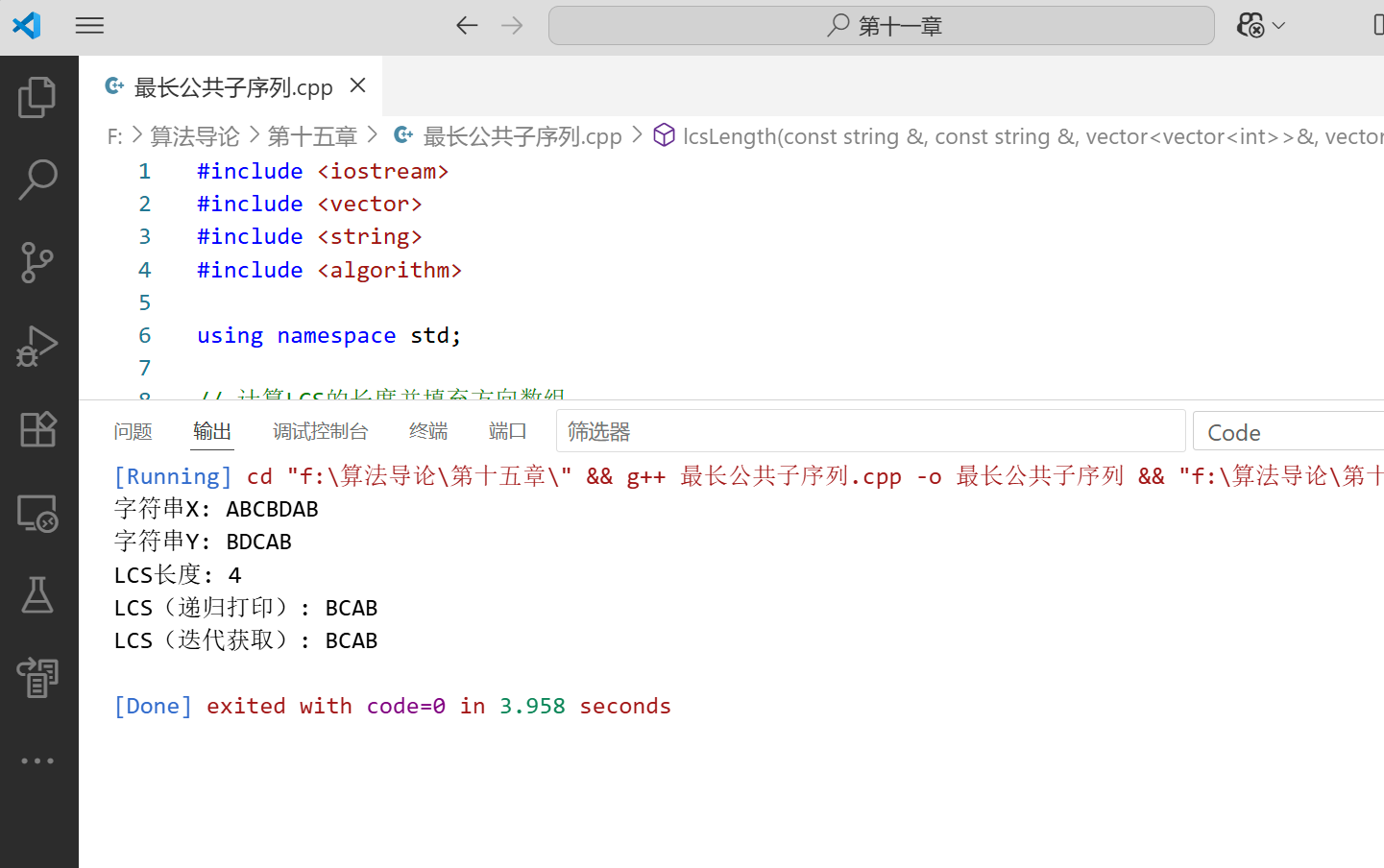
例如,对于字符串 X = \"ABCBDAB\" 和 Y = \"BDCAB\",它们的最长公共子序列是 \"BCAB\",长度为 4。
解法思路
-
最优子结构:设 X [1..i] 和 Y [1..j] 分别表示 X 和 Y 的前 i 和 j 个字符
- 如果 X [i] = Y [j],则 LCS (X [1..i], Y [1..j]) = LCS (X [1..i-1], Y [1..j-1]) + X [i]
- 如果 X [i] ≠ Y [j],则 LCS (X [1..i], Y [1..j]) = max (LCS (X [1..i-1], Y [1..j]), LCS (X [1..i], Y [1..j-1]))
-
动态规划解法:
- 定义 dp [i][j] 为 X [1..i] 和 Y [1..j] 的最长公共子序列的长度
- 定义方向数组 b [i][j] 记录计算 dp [i][j] 时的选择,用于重构 LCS
完整代码实现
#include #include #include #include using namespace std;// 计算LCS的长度并填充方向数组void lcsLength(const string& X, const string& Y, vector<vector>& dp, vector<vector>& b) { int m = X.size(); int n = Y.size(); // 填充dp和b数组 for (int i = 1; i <= m; ++i) { for (int j = 1; j = dp[i][j - 1]) { dp[i][j] = dp[i - 1][j]; b[i][j] = \'|\'; // 向上 } // 如果不匹配,取左方值 else { dp[i][j] = dp[i][j - 1]; b[i][j] = \'-\'; // 向左 } } }}// 递归重构LCSvoid printLCS(const vector<vector>& b, const string& X, int i, int j) { if (i == 0 || j == 0) { return; } // 如果是斜向,表示当前字符属于LCS if (b[i][j] == \'\\\\\') { printLCS(b, X, i - 1, j - 1); cout << X[i - 1]; } // 向上 else if (b[i][j] == \'|\') { printLCS(b, X, i - 1, j); } // 向左 else { printLCS(b, X, i, j - 1); }}// 迭代版本重构LCSstring getLCS(const vector<vector>& b, const string& X, int i, int j) { string lcs; while (i > 0 && j > 0) { if (b[i][j] == \'\\\\\') { lcs.push_back(X[i - 1]); i--; j--; } else if (b[i][j] == \'|\') { i--; } else { j--; } } reverse(lcs.begin(), lcs.end()); return lcs;}int main() { string X = \"ABCBDAB\"; string Y = \"BDCAB\"; int m = X.size(); int n = Y.size(); // dp[i][j]表示X[0..i-1]和Y[0..j-1]的LCS长度 vector<vector> dp(m + 1, vector(n + 1, 0)); // b[i][j]记录计算dp[i][j]时的选择方向 vector<vector> b(m + 1, vector(n + 1, \' \')); // 计算LCS lcsLength(X, Y, dp, b); // 输出结果 cout << \"字符串X: \" << X << endl; cout << \"字符串Y: \" << Y << endl; cout << \"LCS长度: \" << dp[m][n] << endl; cout << \"LCS(递归打印): \"; printLCS(b, X, m, n); cout << endl; string lcs = getLCS(b, X, m, n); cout << \"LCS(迭代获取): \" << lcs << endl; return 0;}代码说明
-
lcsLength 函数:
- 输入:两个字符串 X 和 Y,dp 数组和 b 数组
- 功能:计算 LCS 的长度并填充方向数组
- 实现:使用自底向上的动态规划方法,根据字符是否匹配来决定 dp [i][j] 的值和方向
-
printLCS 函数:
- 输入:方向数组 b,字符串 X,索引 i 和 j
- 功能:递归地打印 X 和 Y 的 LCS
- 实现:根据方向数组的指示,回溯找到 LCS 的各个字符
-
getLCS 函数:
- 输入:方向数组 b,字符串 X,索引 i 和 j
- 功能:迭代地获取 X 和 Y 的 LCS
- 实现:与递归版本思路相同,但使用迭代方式实现,避免了递归调用的开销
-
主函数:
- 定义两个字符串 X 和 Y
- 初始化 dp 和 b 数组
- 调用 lcsLength 计算 LCS
- 分别用递归和迭代方式获取并输出 LCS 及其长度
应用场景
最长公共子序列问题在信息处理中有广泛应用:
- 生物信息学:DNA 序列比对,寻找相似的基因序列
- 文本编辑:计算两个文本的差异,用于版本控制
- 拼写检查:寻找与错误拼写最相似的正确单词
- plagiarism 检测:检测文本之间的相似度
15.5 最优二叉搜索树
问题描述
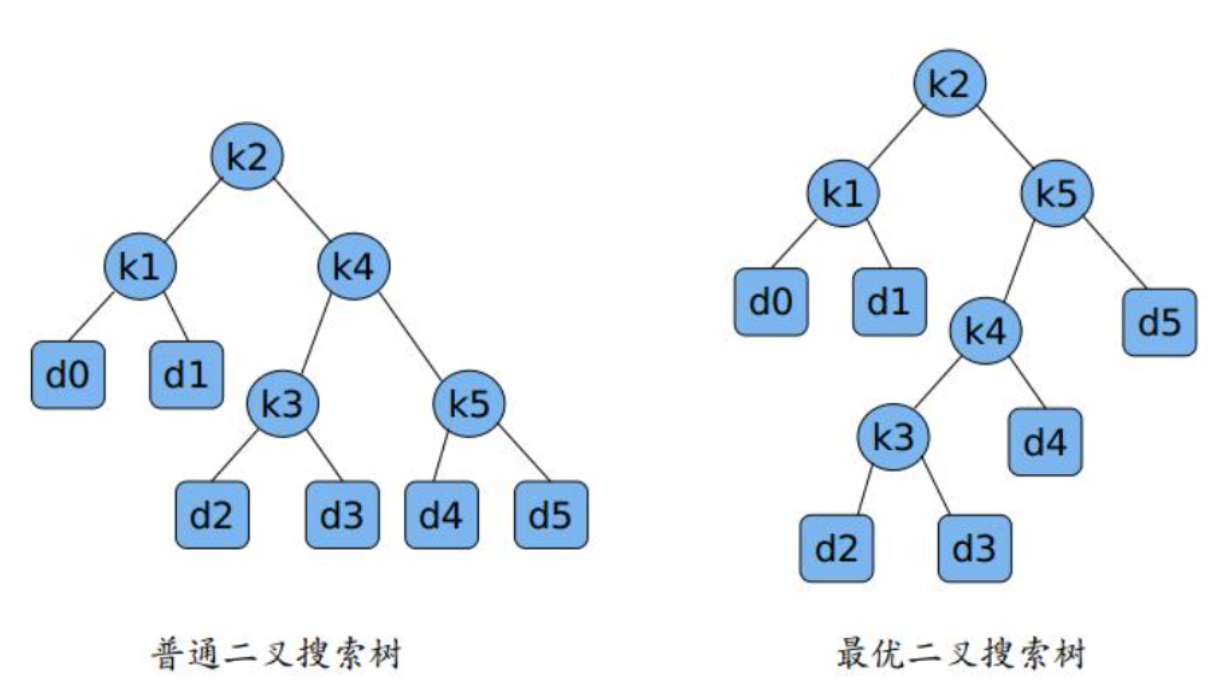
最优二叉搜索树问题研究的是如何构建一棵二叉搜索树,使得搜索的期望代价最小:
- 给定 n 个关键字 k₁ < k₂ < ... < kₙ,以及它们被搜索的概率 p₁, p₂, ..., pₙ
- 同时给定 n+1 个伪关键字 d₀, d₁, ..., dₙ(表示不在关键字集中的值),以及它们被搜索的概率 q₀, q₁, ..., qₙ
- 我们需要构建一棵二叉搜索树,使得搜索的期望代价最小
搜索的期望代价计算公式为:
E [树] = Σ(深度 (kᵢ) + 1)×pᵢ + Σ(深度 (dⱼ) + 1)×qⱼ
其中深度是从根节点到该节点的边数。
解法思路
-
最优子结构:设最优二叉搜索树 T 包含关键字 kᵢ...kⱼ,若其根为 kₖ,则:
- 左子树是包含 kᵢ...kₖ₋₁和 dᵢ₋₁...dₖ₋₁的最优二叉搜索树
- 右子树是包含 kₖ₊₁...kⱼ和 dₖ...dⱼ的最优二叉搜索树
- 期望代价 e [i][j] = e [i][k-1] + e [k+1][j] + w [i][j],其中 w [i][j] 是概率和
-
动态规划解法:
- 定义 e [i][j] 为包含关键字 kᵢ...kⱼ的最优二叉搜索树的期望代价
- 定义 w [i][j] 为关键字 kᵢ...kⱼ和伪关键字 dᵢ₋₁...dⱼ的概率和
- 定义 root [i][j] 记录包含关键字 kᵢ...kⱼ的最优二叉搜索树的根
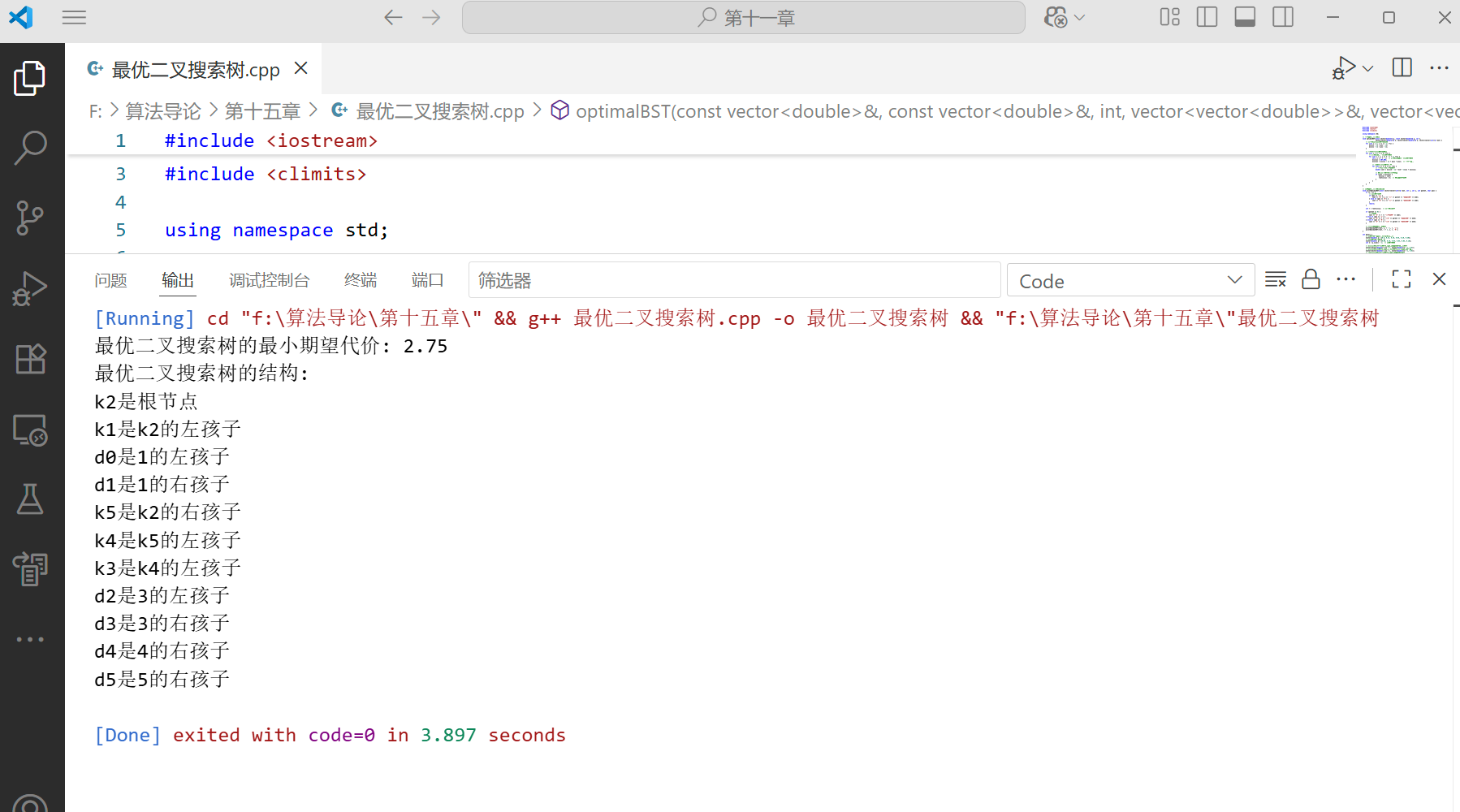
完整代码实现
#include #include #include using namespace std;// 计算最优二叉搜索树void optimalBST(const vector& p, const vector& q, int n, vector<vector>& e, vector<vector>& w, vector<vector>& root) { // 初始化单个伪关键字的情况 for (int i = 1; i <= n + 1; ++i) { e[i][i - 1] = q[i - 1]; w[i][i - 1] = q[i - 1]; } // 计算包含l个关键字的子树 for (int l = 1; l <= n; ++l) { // i是子树的第一个关键字索引 for (int i = 1; i <= n - l + 1; ++i) { int j = i + l - 1; // j是子树的最后一个关键字索引 e[i][j] = INT_MAX; w[i][j] = w[i][j - 1] + p[j] + q[j]; // 计算概率和 // 尝试以每个关键字k为根 for (int k = i; k <= j; ++k) { // 计算当前以k为根的代价 double cost = e[i][k - 1] + e[k + 1][j] + w[i][j]; // 如果当前代价更小,则更新 if (cost < e[i][j]) { e[i][j] = cost; root[i][j] = k; // 记录最佳根节点 } } } }}// 打印最优二叉搜索树的结构void printOptimalBST(const vector<vector>& root, int i, int j, int parent, char pos) { if (i > j) { // 伪关键字节点 if (pos == \'L\') { cout << \"d\" << j << \"是\" << parent << \"的左孩子\" << endl; } else if (pos == \'R\') { cout << \"d\" << j << \"是\" << parent << \"的右孩子\" << endl; } return; } int r = root[i][j]; // 当前子树的根 if (parent == 0) { // 根节点 cout << \"k\" << r << \"是根节点\" << endl; } else if (pos == \'L\') { cout << \"k\" << r << \"是k\" << parent << \"的左孩子\" << endl; } else if (pos == \'R\') { cout << \"k\" << r << \"是k\" << parent << \"的右孩子\" << endl; } // 递归打印左子树和右子树 printOptimalBST(root, i, r - 1, r, \'L\'); printOptimalBST(root, r + 1, j, r, \'R\');}int main() { // 关键字的概率p[1..n],p[0]未使用 vector p = {0.0, 0.15, 0.10, 0.05, 0.10, 0.20}; // 伪关键字的概率q[0..n] vector q = {0.05, 0.10, 0.05, 0.05, 0.05, 0.10}; int n = p.size() - 1; // 关键字数量 // e[i][j]表示包含关键字k_i到k_j的最优BST的期望代价 vector<vector> e(n + 2, vector(n + 1, 0.0)); // w[i][j]表示关键字k_i到k_j和伪关键字d_{i-1}到d_j的概率和 vector<vector> w(n + 2, vector(n + 1, 0.0)); // root[i][j]表示包含关键字k_i到k_j的最优BST的根 vector<vector> root(n + 1, vector(n + 1, 0)); // 计算最优BST optimalBST(p, q, n, e, w, root); // 输出结果 cout << \"最优二叉搜索树的最小期望代价: \" << e[1][n] << endl; cout << \"最优二叉搜索树的结构:\" << endl; printOptimalBST(root, 1, n, 0, \' \'); return 0;}代码说明
-
optimalBST 函数:
- 输入:关键字概率 p,伪关键字概率 q,关键字数量 n,e、w 和 root 数组
- 功能:计算最优二叉搜索树的期望代价和结构
- 实现:使用自底向上的动态规划方法,按照子树包含的关键字数量递增的顺序计算
-
printOptimalBST 函数:
- 输入:root 数组,子树的关键字范围 i 和 j,父节点索引 parent,位置 pos
- 功能:递归地打印最优二叉搜索树的结构
- 实现:根据 root 数组确定当前子树的根,然后递归打印左子树和右子树
-
主函数:
- 定义关键字概率 p 和伪关键字概率 q
- 初始化 e、w 和 root 数组
- 调用 optimalBST 计算最优二叉搜索树
- 输出最小期望代价和最优二叉搜索树的结构
应用场景
最优二叉搜索树问题在信息检索和数据库系统中有重要应用:
- 搜索引擎:优化关键词搜索的效率
- 数据库索引:设计高效的 B 树或 B + 树索引
- 编译器:优化符号表的查询效率
- 自动补全:优化用户输入的预测和补全
思考题
-
设计一个动态规划算法,求解有向无环图(DAG)中两个节点之间的最长路径问题。
-
考虑 0-1 背包问题:有 n 个物品,每个物品有重量 wᵢ和价值 vᵢ,背包容量为 W。如何选择物品放入背包,使得总价值最大且总重量不超过 W?设计一个动态规划算法解决该问题。
-
编辑距离问题:给定两个字符串 X 和 Y,定义三种操作:插入一个字符、删除一个字符、替换一个字符,每种操作都有相应的代价。求将 X 转换为 Y 的最小代价。设计一个动态规划算法解决该问题。
-
假设你是一个小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
本章注记
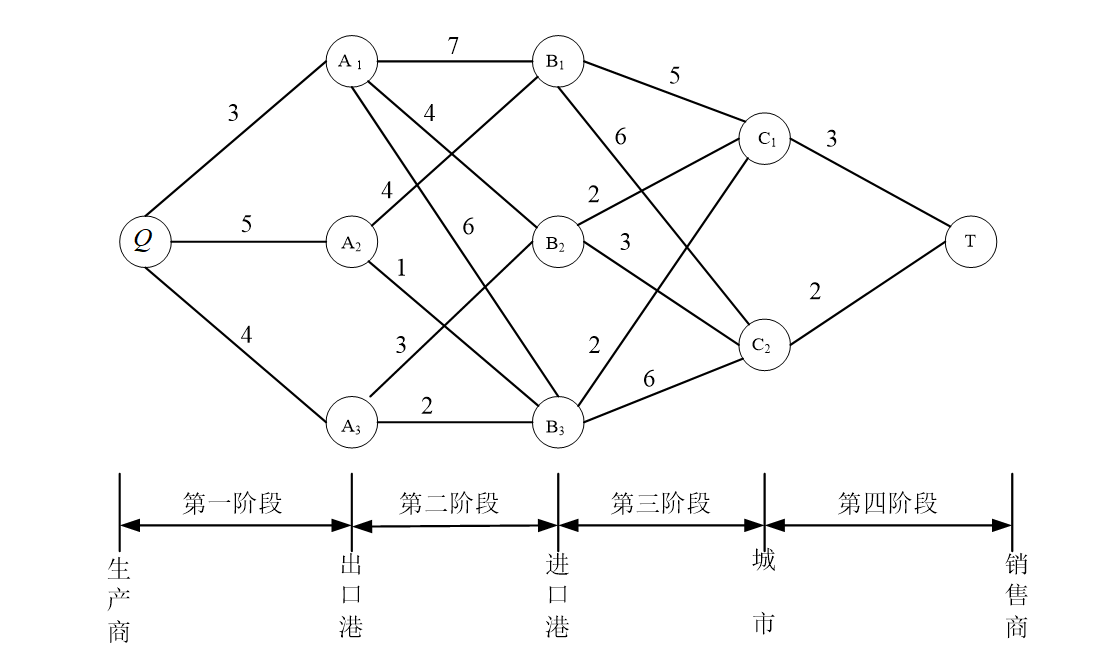
动态规划作为一种重要的算法设计技术,最早可以追溯到 20 世纪 50 年代,由美国数学家理查德・贝尔曼(Richard Bellman)提出。他在研究多阶段决策过程的优化问题时,系统地发展了这一方法,并将其应用于控制论和运筹学等地方。

动态规划的核心思想是将复杂问题分解为重叠子问题,并利用子问题的最优解来构建原问题的最优解。这种思想在许多领域都有广泛应用,如:
- 经济学:最优投资策略
- 工程学:控制系统设计
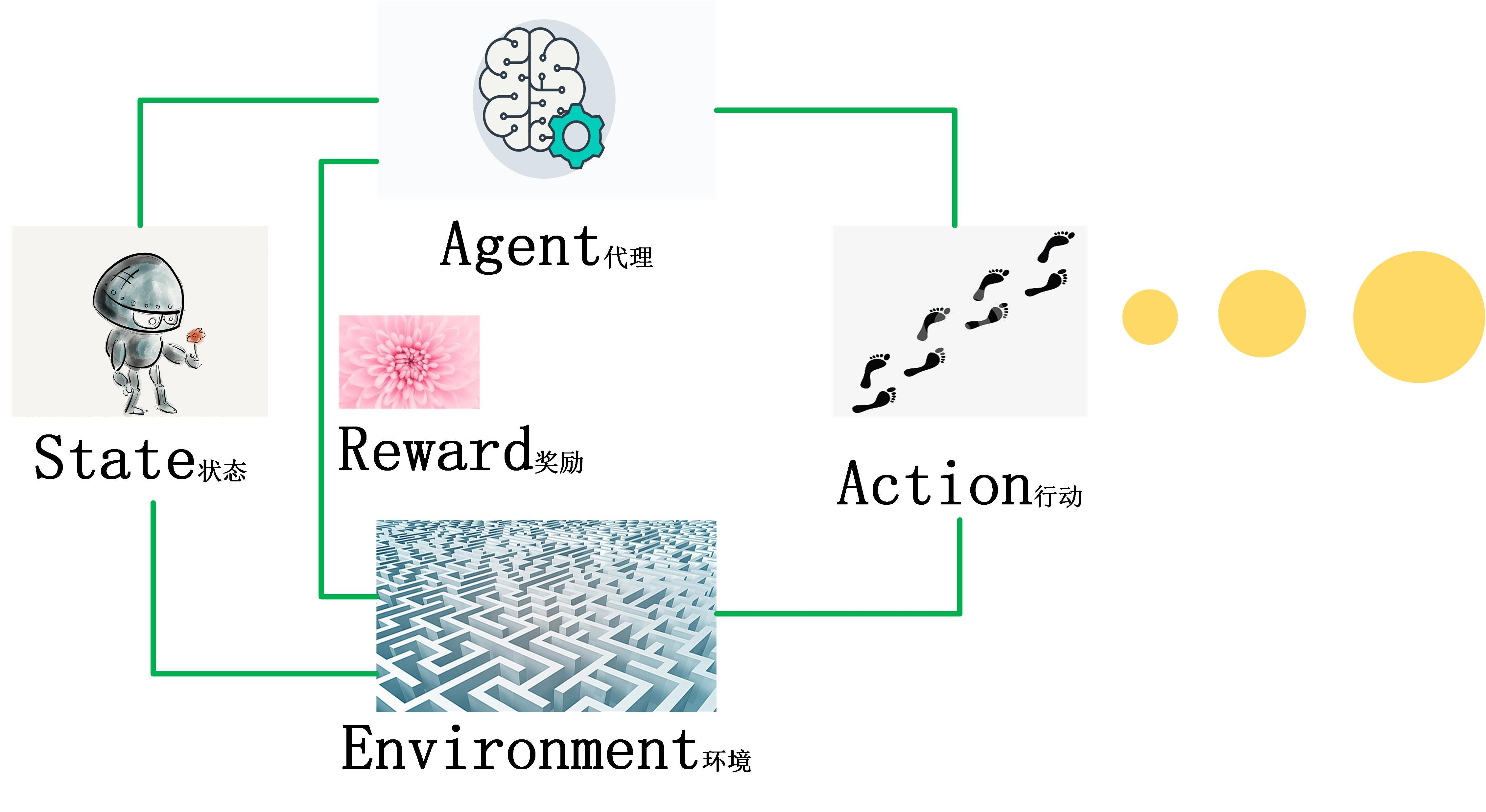
- 人工智能:强化学习中的价值函数估计
- 生物信息学:序列比对和基因预测
随着问题规模的增大,动态规划的时间和空间复杂度可能会急剧增加。为了应对这一挑战,研究人员提出了许多优化技术,如:
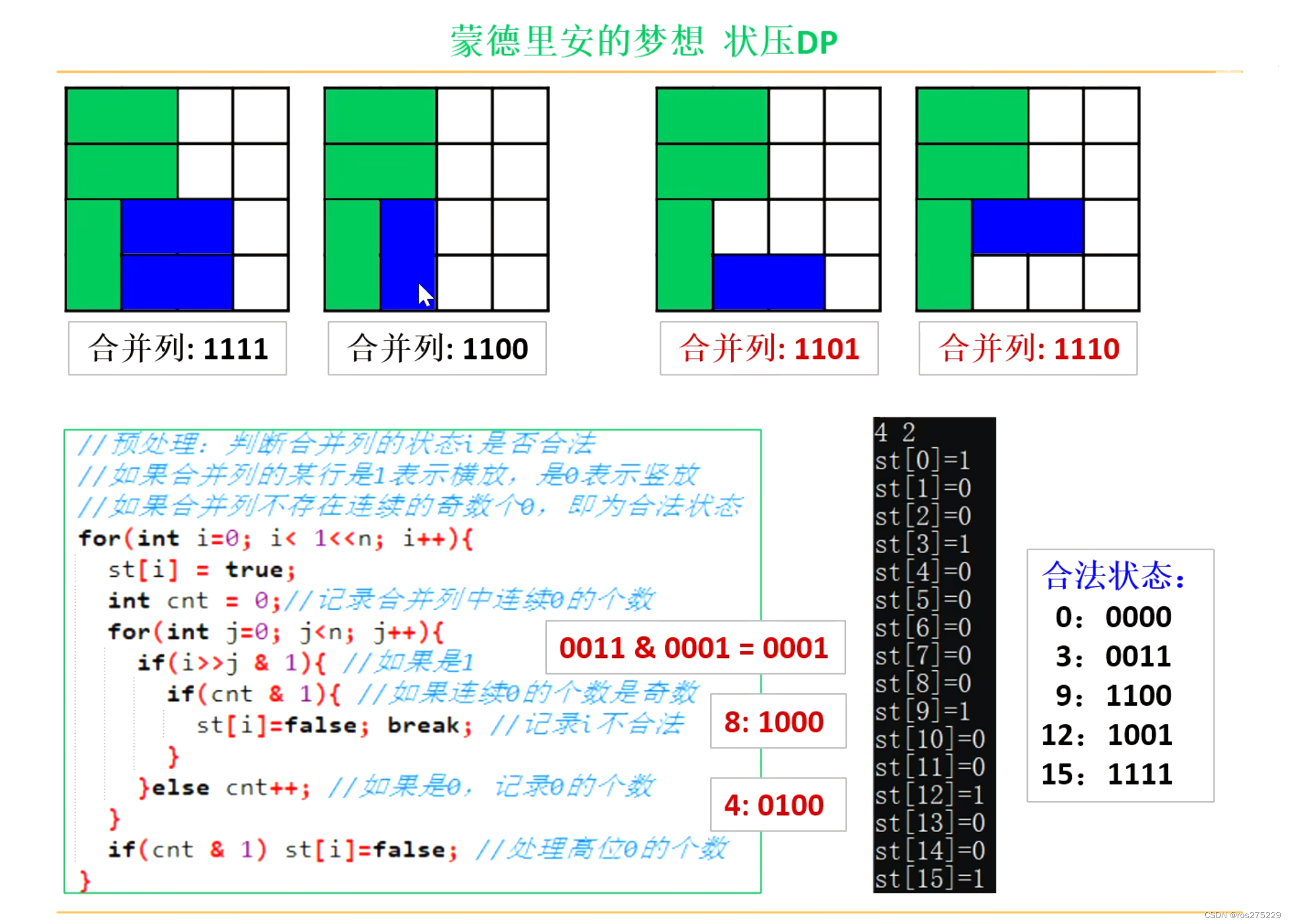
- 状态压缩:减少存储状态所需的空间
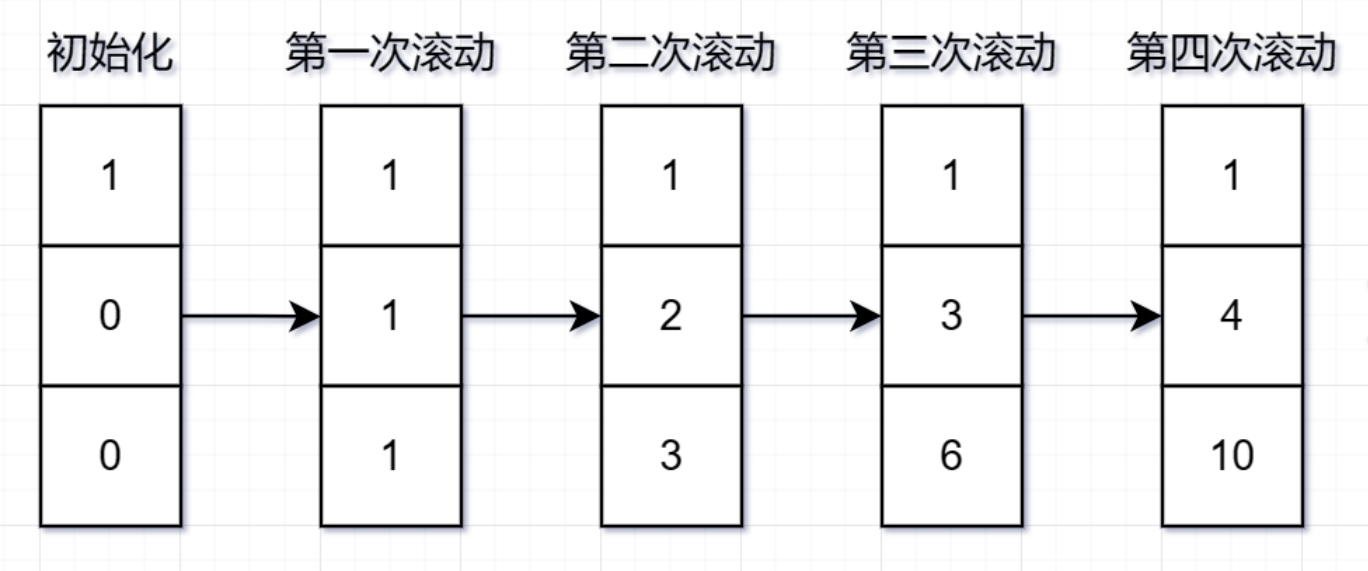
- 滚动数组:只保存必要的子问题解
- 并行计算:利用多核处理器加速计算
动态规划与其他算法设计技术(如贪心算法、分治算法)既有联系又有区别:
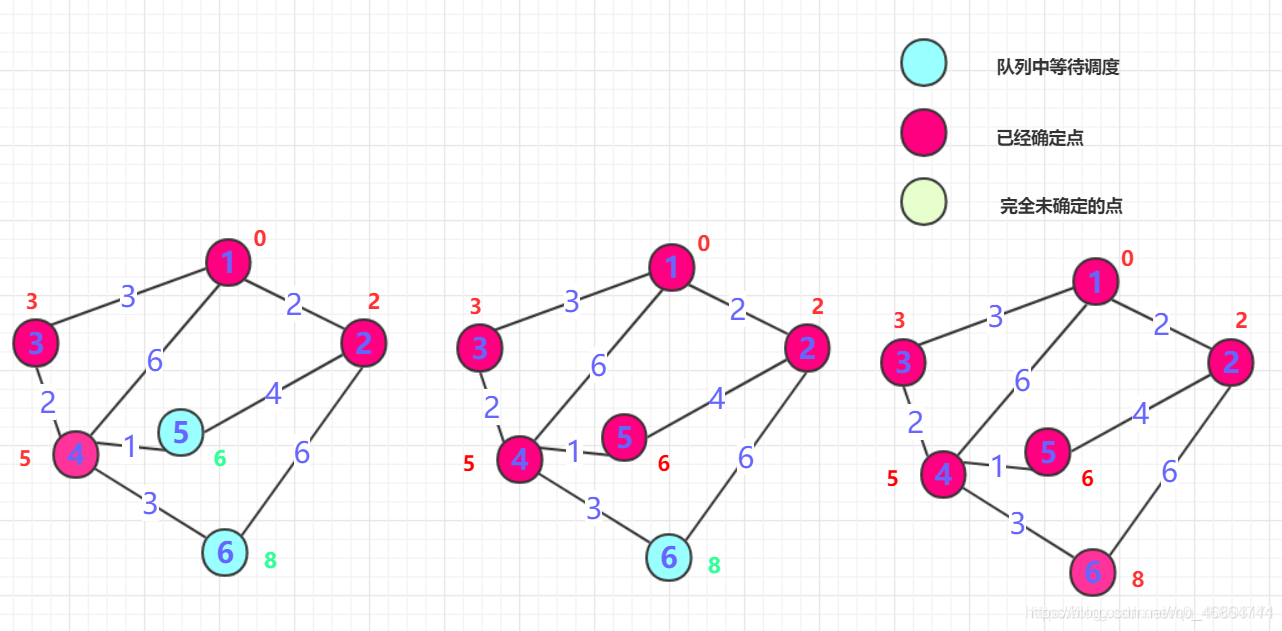
- 与贪心算法相比,动态规划通常能得到全局最优解,但计算成本更高
- 与分治算法相比,动态规划适用于子问题重叠的情况,通过存储子问题解来避免重复计算

掌握动态规划不仅有助于我们解决复杂的优化问题,更重要的是培养一种分解问题、寻找规律的思维方式,这对于解决各种实际问题都具有重要意义。

希望本章的内容能帮助大家理解和掌握动态规划这一强大的算法设计技术。如果有任何疑问或建议,欢迎在评论区留言讨论!