数据结构（排序篇）——七大排序算法奇幻之旅：从扑克牌到百亿数据的魔法整理术

数据结构专栏 ⬅(click)

---

开篇：当数据开始\"排队\"

想象你是一位扑克牌魔术师（没错，就是那种能把一副乱序的牌瞬间理整齐的酷炫角色）。今天，我要揭秘的正是计算机世界中最神奇的\"整理魔法\"——排序算法！准备好你的魔杖（键盘），我们开始这场奇幻之旅吧！

第一章：基础魔法——排序概念入门

1.1 什么是排序？

“把大象装冰箱需要三步，把数据排好序也只需要三步：比较、移动、重复” —— 某不愿透露姓名的算法魔法师

稳定性魔咒：

• 稳定魔法：5₁和5₂这两个相同数字，排序后保持原始顺序
• 不稳定魔法：5₁和5₂可能交换位置

1.2 内存中的魔法 vs 磁盘上的魔法

• 内部排序：所有数据都在内存中（像在桌子上整理扑克牌）
• 外部排序：数据太大要借助磁盘（像整理一个图书馆的书籍）

第二章：七大排序魔法详解

2.1 插入排序——扑克牌大师的秘技

思路：整个数组划分为有序区间和无序区间，每次取出无序区间一个元素，插入到有序区间的合适位置
整个过程循环n-1次,时间复杂度O(n²)，空间复杂度O(1)

 private static void insertSort(int[] arr){ // bond是有序和无序的边界 for(int bond = 1; bond < arr.length; bond++){ int value = arr[bond]; int cur = bond-1; for (;cur>=0;cur--){ if(arr[cur]>value){  //这种情况就需要搬运，把cur位置的元素搬运到cur+1的位置  arr[cur+1] = arr[cur]; }else {  //此时说明已经到达合适位置，退出循环直接插入即可  break; } } //意味着将value应该放在cur之后，也就是cur+1的位置 arr[cur+1] = value; } }

• 最佳情况：O(n)（当牌已经基本有序时）
• 最差情况：O(n²)（当牌完全逆序时）
• 稳定性：✔️（相同点数的牌保持顺序）

2.2 希尔排序——分组跳跃的魔法（插入排序的plus）

• 思路：先把整个数组分成若干组，针对每个数组分别进行插入排序
  希尔排序,分组插排操作,不是只进行一次,而是要进行若干次的~~
  比如 指定 gap 为 3 2 1 这样的序列
  先按照 gap 为 3 进行分组插排
  再按照 gap 为 2 进行分组插排
  最后按照 gap 为1进行分组插排 (就相当于普通的插入排序) =>肯定能保证有序的
• 普通的插入排序:
  1.如果要排序的数组,很短,整体的效率就很高.
  2.如果要排序的数组,已经基本有序,整体效率也很高
  当 gap 的值比较大的时候,分出的组就多，每个组的元素就少.针对每个组分别插排,都很快
  当 gap 的值比较小的时候,分的组是少了,通过前面的准备工作,已经使整个数组相对来说比较有序了.这个时候意味着此时的速度也很快~~
• 时间复杂度最坏为O(n²)，平均复杂的根据gap值来确定，gap一般取值size/2，size/2，size/4 ……空间复杂度为O(1)

 private static void shellSort(int[] arr){ int gap = arr.length/2; while(gap>=1){ //针对每个组进行插入排序 insertSortGap(arr, gap); //添加一个打印，看每次gap的效果 System.out.println(\"gap = \" + gap + \" : \" + Arrays.toString(arr)); gap /= 2; } } private static void insertSortGap(int[] arr, int gap){ // 分组插入排序 // 每个组中的元素，下标差值为gap // 例如，gap为3的时候，组为[0，3)，[3，6)，[6，9) // 此处同一个组内部的元素下标差值是gap。取下一个元素看起来是bound += gap // 但是此处的处埋，其实是针对所有的组，同时处理 // 比如gap为3，则有3个组，比如是0，1，2 // bound 的循坏过程，就是在处理第 0 组的第1个元素的插入，再处理第1组的第1个元素的插入，再处理第2组的第1个元素的插入 // 然后再处理第0组的第2个元素的插入，再处理第1组的第2个元素的插入，再处理第2组的第2个元素的插入.以此类推 for (int bond = gap; bond < arr.length; bond++){ int value = arr[bond]; int cur = bond - gap; for (;cur>=0;cur-=gap){ if(arr[cur]>value){  arr[cur + gap] = arr[cur]; }else{  break; } } arr[cur + gap] = value; } }

未解之谜：希尔排序的时间复杂度至今仍是算法界的\"魔法谜题\"，不同魔法师给出了不同的答案：

• O(n^1.25) ~ O(1.6n^1.25)（Knuth的猜想）
• O(n^1.3)（实验统计结果）
• O(n log²n)（某些特定间隔序列）
• 稳定性：❌

2.3 直接选择排序——打擂主的挑战赛

• 思路： 把整个数组划分成两个区间,前半部分已排序区间(有序区间),后半部分是待排序区间(无序区间)初始情况下,有序区间是空区间
• 从无序区间中,找出整个无序区间里的最小值,把这个最小值,和无序区间的第一个元素交换同时把这个无序区间的第一个元素,划分到有序区间中每次进行一趟,都会使有序区间变大一点~~
• 这个找最小的过程，通过\"打擂主”的方式，以待排序区间的第一个元素位置作为“擂主”
• 拿着后续的每个元素都和擂台上的元素进行比较。如果比擂台元素小，就交换.

 private static void selectSort(int[] arr){ // [0, bond)已排序区间 [bond,arr.length)未排序区间 for(int bond = 0;bond<arr.length-1;bond++){ for(int cur = bond+1;cur<arr.length;cur++){ if(arr[bond]>arr[cur]){  //打擂成功，进行交换  int temp = arr[bond];  arr[bond] = arr[cur];  arr[cur] = temp; } } //打印执行效果 System.out.println(\"bond = \" + bond + \" : \" + Arrays.toString(arr)); } }

• 时间复杂度O(n²)
• 空间复杂度O(1)
• 不稳定排序

2.4 堆排序——懂得利用工具的算法

• 堆排序的基本思想:
  1.针对整个数组,建立大堆.(初始情况下,整个数组,都是\"待排序区间\")
  2.把堆顶元素和待排序区间的最后一个元素,交换.(把最大元素就放到已排序区间中了)
  3.把堆顶元素进行向下调整,确保前面堆的结构仍然合法的,

public static void heapSort(int[] arr){ creatHeap(arr); int bond = arr.length - 1; for (int i = 0;i<arr.length;i++){ int temp = arr[0]; arr[0] = arr[bond]; arr[bond] = temp; shiftDown(arr, bond, 0); bond--; //将最后一个元素添加到已排序部分 } } //建大堆 public static void creatHeap(int[] arr){ int lastLeaf = arr.length - 1; for (int i = lastLeaf-1;i>=0;i--){ shiftDown(arr, arr.length, i); } } //向下调整 public static void shiftDown(int[] arr, int len, int index){ int parent = index; int child = 2 * parent + 1; while (child < len){ if(child + 1 < len && arr[child] < arr[child+1]){ child += 1; } if(arr[child] > arr[parent]){ int temp = arr[parent]; arr[parent] = arr[child]; arr[child] = temp; }else { break; } parent = child; child = 2 * parent + 1; } }

• 时间复杂度O(NlogN)
• 空间复杂度O(1)
• 不稳定排序

2.5 冒泡排序——沉浮的法则

• 冒泡排序比较交换相邻元素，这样的一趟下来就能把最大值放到最后.(或者从后往前遍历,此时就能把最小值放到最前)

public static void bubbleSort(int[] arr){ for (int bond = 0; bond < arr.length - 1; bond++) { for(int cur = arr.length - 1;cur > bond;cur--){ if(arr[cur - 1] > arr[cur]){  int temp = arr[cur - 1];  arr[cur - 1] = arr[cur];  arr[cur] = temp; } } System.out.println(Arrays.toString(arr)); } }

• 时间复杂度O(N²)
• 空间复杂度O(1)
• 稳定排序

2.6 快速排序（Hoare版本）——分而治之的闪电魔法

• 寻找基准值方法
• 针对left，right 闭区间，进行整理,
• 注意选择基准值的位置，和后续两个下标运动的先后顺是有关的：
  1. 如果选择最右侧元素为基准值，就需要先从左往右找比基准值大的，后从右往左找比基准值小的
  2. 如果选择最左侧元素为基准值，就需要先从右往左找比基准值小的，后从左往右找比基准值大的.

快速排序（递归版）

// 方法入口 //此处约定[left，right]闭区间为待处理区间 public static void quickSort(int[] arr){ quickSort(arr, 0, arr.length-1); } //辅助递归工具 public static void quickSort(int[] arr, int left, int right){ //结束递归条件（当前区间为空区间或者只有一个元素） if(left>=right){ return; } int index = partition(arr, left, right); //对基准值左边进行递归 quickSort(arr, left, index-1); //对基准值右边进行递归 quickSort(arr, index+1, right); } //寻找基准值方法 private static int partition(int[] arr, int left, int right){ // 选取最右边元素为基准值 int pivot = arr[right]; int l = left; int r = right; while (l < r){ while (l<r && arr[l]<=pivot){ l++; } while (l<r && arr[r]>=pivot){ r--; } swap(arr, l, r); } //最外层循环结束后要交换重合值和基准值 swap(arr, l, right); return l; } //交换方法 private static void swap(int[] arr, int left, int right){ int temp = arr[left]; arr[left] = arr[right]; arr[right] = temp; }}

快速排序(循环版)

 // 快速排序(非递归版本) static class Range{ private int left; private int right; public Range(int left, int right){ this.left = left; this.right = right; } } public static void quickSortByLoop(int[] arr){ //利用栈模拟递归过程 Stack<Range> range = new Stack<>(); range.push(new Range(0, arr.length - 1)); while (!range.isEmpty()){ Range top = range.pop(); if(top.left >= top.right){ continue; } int pivot = Partition(arr, top.left, top.right); range.push(new Range(top.left, pivot - 1)); range.push(new Range(pivot + 1, top.right)); } //当循环结束时，排序就已经完成了 } public static int Partition(int[] arr, int left, int right){ int pivot = arr[left]; int l = left; int r = right; while (l<r){ while (l<r && arr[r]>=pivot){ r--; } while (l<r && arr[l]<=pivot){ l++; } swap(arr, l, r); } //记住传参是传基准值的下标而不是直接传基准值 swap(arr, l, left); return l; } public static void swap(int[] arr, int i, int j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }

• 基准选择：三数取中法(减少取到极端值的概率)或者选择最右边或者最左边
• 时间复杂度：最坏O(N²) 平均O(NlogN)
• 空间复杂度：最坏O(N) 平均O(logN)
• 不稳定排序

2.7 归并排序——耐心的拼图魔法

• 归并排序的核心流程分为两步：

1. 拆分（Divide）：将数组不断二分，直到每个子数组只包含 1 个元素（天然有序）。
2. 合并（Merge）：将两个有序子数组合并为一个更大的有序数组，重复此过程直到合并为完整数组。

 public static void mergeSort(int[] arr){ mergeSort(arr, 0, arr.length-1); } //归并排序的辅助方法。参数中引入子区间，通过子区间来进行决定当前是要针对哪个部分的数组进行归并排序 public static void mergeSort(int[] arr, int left, int right){ //1.如果子区间只有一个或者没有元素，则不需要递归 if(left>=right)return; //2.把当前区间分为两个等长区间，分别进行递归 int mid = (left + right)/2; //3.递归左半边和递归右半边 // 快速排序是分成三个部分，基准值是单独一个部分，左右递归时，需要把基准值位置给去除 // 归并排序是分成两个部分，mid这个位置的元素也要参与递归 mergeSort(arr, left, mid); mergeSort(arr, mid+1, right); //4.完成上述递归后说明左右两个区间已经是有序的了，开始合并 merge(arr, left, mid, right); } private static void merge(int[] arr, int left, int mid, int right){ //1.先创建一个临时数组保存结果，临时数组的长度应该是right-left+1 int[] result = new int[right - left + 1]; //后续合并时候，要把对应的元素进行尾插到尾插到result中的，使用resultSize表示result中已经插入的元素个数 //此处就是在模拟简单的顺序表 int resultSize = 0; //2.设定两个下标指向每个区间的开头 int cur1 = left; int cur2 = mid + 1; while (cur1 <= mid && cur2 <= right){ if(arr[cur1] < arr[cur2]){ // 把cur1位置的元素插到result中 result[resultSize++] = arr[cur1]; cur1++; }else { result[resultSize++] = arr[cur2]; cur2++; } } //3.处理剩余的元素，由于这两个区间的长度不一定完全相同，只需要把多余的部分，整体尾插到result中即可 while (cur1<=mid){ result[resultSize++] = arr[cur1]; cur1++; } while (cur2<=right){ result[resultSize++] = arr[cur2]; cur2++; } for (int i = 0; i < resultSize; i++){ arr[left+i] = result[i]; } }

• 时间复杂度：O(NlogN)
• 空间复杂度：O(N)
• 稳定排序

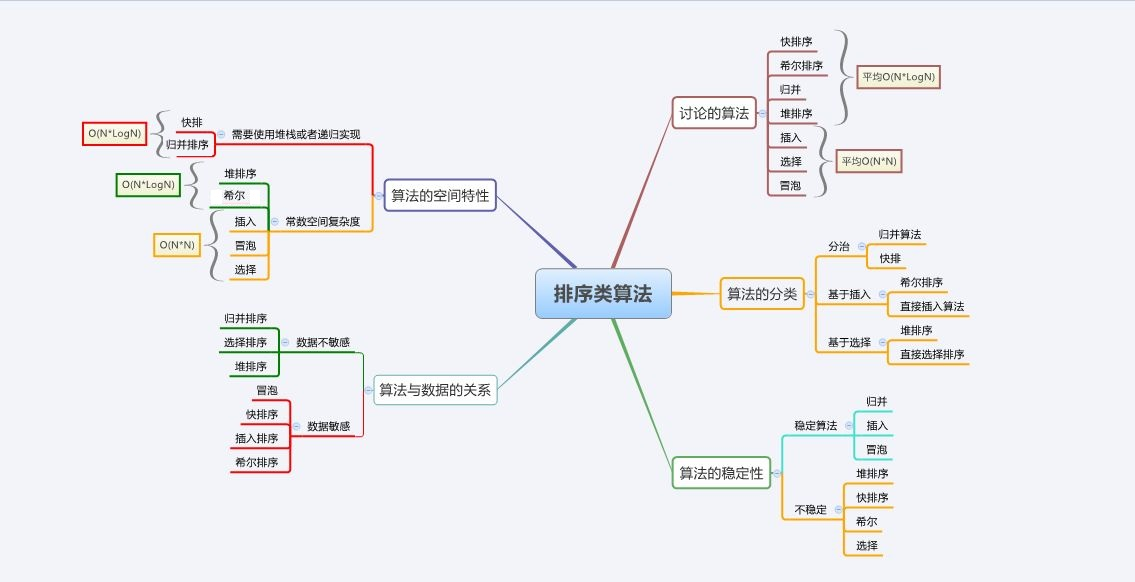
第三章：性能比较

3.1 七大排序性能表

排序魔法 平均时间复杂度 最坏情况 空间复杂度 稳定性 适用场景 冒泡排序 O(n²) O(n²) O(1) ✔️ 教学演示 选择排序 O(n²) O(n²) O(1) ❌ 交换成本高时 插入排序 O(n²) O(n²) O(1) ✔️ 小数据/基本有序 希尔排序 O(n log n) O(n²) O(1) ❌ 中等规模数据 归并排序 O(n log n) O(n log n) O(n) ✔️ 大数据/需要稳定 快速排序 O(n log n) O(n²) O(log n) ❌ 通用场景 堆排序 O(n log n) O(n log n) O(1) ❌ 内存受限时

3.2 算法选择指南（思维导图版）

#mermaid-svg-MOQkaJr3XoYbUHbZ {font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .error-icon{fill:#552222;}#mermaid-svg-MOQkaJr3XoYbUHbZ .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-MOQkaJr3XoYbUHbZ .marker{fill:#333333;stroke:#333333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .marker.cross{stroke:#333333;}#mermaid-svg-MOQkaJr3XoYbUHbZ svg{font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-MOQkaJr3XoYbUHbZ .label{font-family:\"trebuchet ms\",verdana,arial,sans-serif;color:#333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .cluster-label text{fill:#333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .cluster-label span{color:#333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .label text,#mermaid-svg-MOQkaJr3XoYbUHbZ span{fill:#333;color:#333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .node rect,#mermaid-svg-MOQkaJr3XoYbUHbZ .node circle,#mermaid-svg-MOQkaJr3XoYbUHbZ .node ellipse,#mermaid-svg-MOQkaJr3XoYbUHbZ .node polygon,#mermaid-svg-MOQkaJr3XoYbUHbZ .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-MOQkaJr3XoYbUHbZ .node .label{text-align:center;}#mermaid-svg-MOQkaJr3XoYbUHbZ .node.clickable{cursor:pointer;}#mermaid-svg-MOQkaJr3XoYbUHbZ .arrowheadPath{fill:#333333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-MOQkaJr3XoYbUHbZ .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-MOQkaJr3XoYbUHbZ .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-MOQkaJr3XoYbUHbZ .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-MOQkaJr3XoYbUHbZ .cluster text{fill:#333;}#mermaid-svg-MOQkaJr3XoYbUHbZ .cluster span{color:#333;}#mermaid-svg-MOQkaJr3XoYbUHbZ div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-MOQkaJr3XoYbUHbZ :root{--mermaid-font-family:\"trebuchet ms\",verdana,arial,sans-serif;} 小数据 中等数据 大数据 是 否 是 否 需要排序? 数据规模 插入排序 快速排序/希尔排序 是否需要稳定? 归并排序 快速排序/堆排序 内存限制? 堆排序

第四章：现实中的魔法应用

4.1 百亿数据排序——外部排序的魔法

当你的数据比内存还大时（比如100G数据，只有1G内存）：

1. 分割阶段：将大文件切成200份512M的小文件（就像把一座山分成可搬运的石头）
2. 排序阶段：分别对每个小文件排序（在内存中整理每块石头）
3. 归并阶段：使用2路归并逐步合并（把整理好的石头重新组装成山）

// 伪代码：外部排序的魔法仪式public void externalSort(File bigFile) { List<File> chunks = splitIntoChunks(bigFile, 512MB); // 第一步：分割 for (File chunk : chunks) { sortInMemory(chunk); // 第二步：内存排序 } mergeSortedChunks(chunks); // 第三步：归并}

---

现在，你已经成为了一名合格的\"排序魔法师\"！下次当你看到杂乱的数据时，记得选择合适的\"魔法\"来驯服它们。记住，没有最好的魔法，只有最适合的魔法！✨