动态规划1

爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2输出：2解释：有两种方法可以爬到楼顶。1. 1 阶 + 1 阶2. 2 阶

示例 2：

输入：n = 3输出：3解释：有三种方法可以爬到楼顶。1. 1 阶 + 1 阶 + 1 阶2. 1 阶 + 2 阶3. 2 阶 + 1 阶

提示：

• 1 <= n <= 45

我的思路：

这个问题，如果顺着去想，会发现特别的复杂，每个台阶都可以选择走1步或2步，顺着很难计算。逆向思考一下，我在这个台阶，有可能我是从下面一个台阶上来的，也可能是从下两个台阶上来的，所以到达我这个台阶的方式应该是 下面一个台阶的方式数 + 下面两个台阶的方式数。抽象出来就是一个递归问题 和 动态规划问题。

只有一个台阶的话，就不用爬，那不用爬是0种方式还是1种方式呢？

等等！n>=1，说明最少都有2级台阶，所以只要考虑最小的2级台阶就行了。这样就不存在上面的问题啦！

// 代码1（错误）int stepNumber1(int n) {    if (n == 1) { // n=1说明有2级台阶，往上爬1个台阶即可        return 1;   }    return stepNumber1(n - 1) + stepNumber1(n - 2); // 此时出现了问题，n=2时有个stepNumber1(0)，这个是在考虑之外的，所以我们多考虑一步，把n=2的情况也算出来}​// 代码1（正确）int stepNumber2(int n) {    if (n == 1) {        return 1;   }    if (n == 2) { // n=2，有3级台阶，可以从起点爬2级，也可以从起点1级1级的爬        return 2;   }    return stepNumber2(n - 1) + stepNumber2(n - 2);}

优化：

我们观察这个代码，很明显的是斐波那契数列的递推式，1，2，3，5......第三个数是前两个数之和。

可以用记忆化搜索解决：

vector arr(50, -1);int stepNumber(int n) { if (n == 1 || n == 2) {        arr[n] = n;   }    if (arr[n] == -1) { // 把计算过的存起来        arr[n] = stepNumber(n - 1) + stepNumber(n - 2);   }    return arr[n];}

也可以改成迭代的方式：

class Solution {public:    int climbStairs(int n) {        if(n == 1) return 1;        if(n == 2) return 2;        int a = 1, b = 2, c = 3;        for(int i = 3; i <= n; i++) {            c = a + b;            a = b;            b = c;       }        return c;   }};

第n个泰波那契数列

泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例 1：

输入：n = 4输出：4解释：T_3 = 0 + 1 + 1 = 2T_4 = 1 + 1 + 2 = 4

示例 2：

输入：n = 25输出：1389537

提示：

• 0 <= n <= 37

• 答案保证是一个 32 位整数，即 answer <= 2^31 - 1

我的思路：这个和经典的求斐波那契数列如出一辙，只是要求的项比较大，直接递归无法解决，使用记忆化计算或迭代都可以。

vector arr(50, -1);int tribonacci_n(int n) { if (n == 0 || n == 1) {        arr[n] = n;   }    if (n == 2) {        arr[n] = 1;   }    if (arr[n] == -1) {        arr[n] = tribonacci_n(n - 1) + tribonacci_n(n - 2) + tribonacci_n(n - 3);   }    return arr[n];}

迭代：

int arr[50] = {0};int tribonacci_n(int n) { arr[0] = 0;    arr[1] = 1;    arr[2] = 1;    for (int i = 3; i <= n; ++i) {        arr[i] = arr[i - 1] + arr[i - 2] + arr[i - 3];   }    return arr[n];}

因为它只要第几个，所以前面的过程都可以不记录，用几个临时变量存储、交换即可，代码就不写了很简单。

使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]输出：15解释：你将从下标为 1 的台阶开始。- 支付 15 ，向上爬两个台阶，到达楼梯顶部。总花费为 15 。

示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]输出：6解释：你将从下标为 0 的台阶开始。- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。- 支付 1 ，向上爬一个台阶，到达楼梯顶部。总花费为 6 。

提示：

• 2 <= cost.length <= 1000

• 0 <= cost[i] <= 999

我的思路：

类似的问题是爬楼梯问题，这抽象出来也是个动态规划问题。一般遇到问题之间有覆盖包含关系的，都先考虑一下动态规划。

Fn = min ( Fn-1 + cost[n], Fn-2 + cost[n])

F0 = cost[0]

F1 = cost[1]

其中，Fn代表从第n级台阶起跳后的总花费（做完后查看官方题解，它是以dp[n]为到达顶楼的花费，即n为顶楼，代码最后给出）。

int F(int n, vector& cost) {    if (n == 0 || n == 1) {        return cost[n];   }    return min(F(n - 1, cost), F(n - 2, cost)) + cost[n];}class Solution {public:    int minCostClimbingStairs(vector& cost) {        return min(F(cost.size() - 1, cost), F(cost.size() - 2, cost));   }};

优化（记忆化搜索/剪枝）：

vector arr(1005, -1);int F(int n, vector& cost) {    if (n == 0 || n == 1) {        arr[n] = cost[n];   }    if (arr[n] == -1) {        arr[n] = min(F(n - 1, cost), F(n - 2, cost)) + cost[n];   }    return arr[n];}class Solution {public:    int minCostClimbingStairs(vector& cost) {        return min(F(cost.size() - 1, cost), F(cost.size() - 2, cost));   }};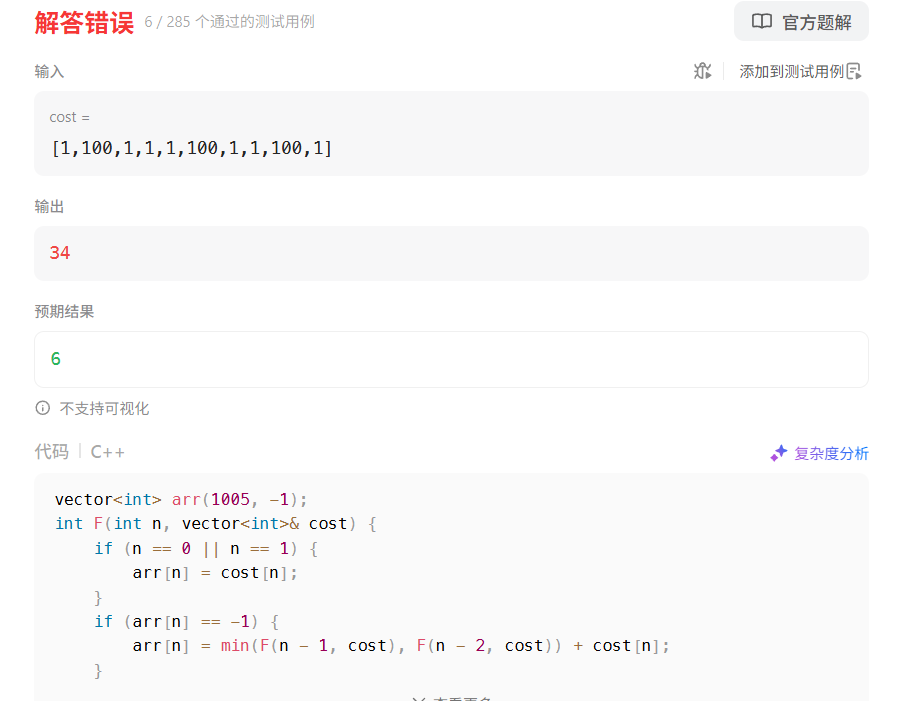

咦！好奇怪的问题啊，我反复检查了很多很多次，都没有发现问题。然后我就开始打印内容，我发现在调用之前打印数组，内容居然不全是-1，哦哦哦！LeetCode这么搞是吧！它是把你的程序运行一次，然后不断的给输出，所以你的程序要保证幂等性。它不像ACM的每个测试用例都重新运行一遍代码！！！

改一下代码：

vector arr(1005, -1);int F(int n, vector& cost) {    if (n == 0 || n == 1) {        arr[n] = cost[n];   }    if (arr[n] == -1) {        arr[n] = min(F(n - 1, cost), F(n - 2, cost)) + cost[n];   }    return arr[n];}class Solution {public:    int minCostClimbingStairs(vector& cost) {        int ans = min(F(cost.size() - 1, cost), F(cost.size() - 2, cost)); // 存结果        arr.assign(1005, -1); // 重置数组        return ans;   }};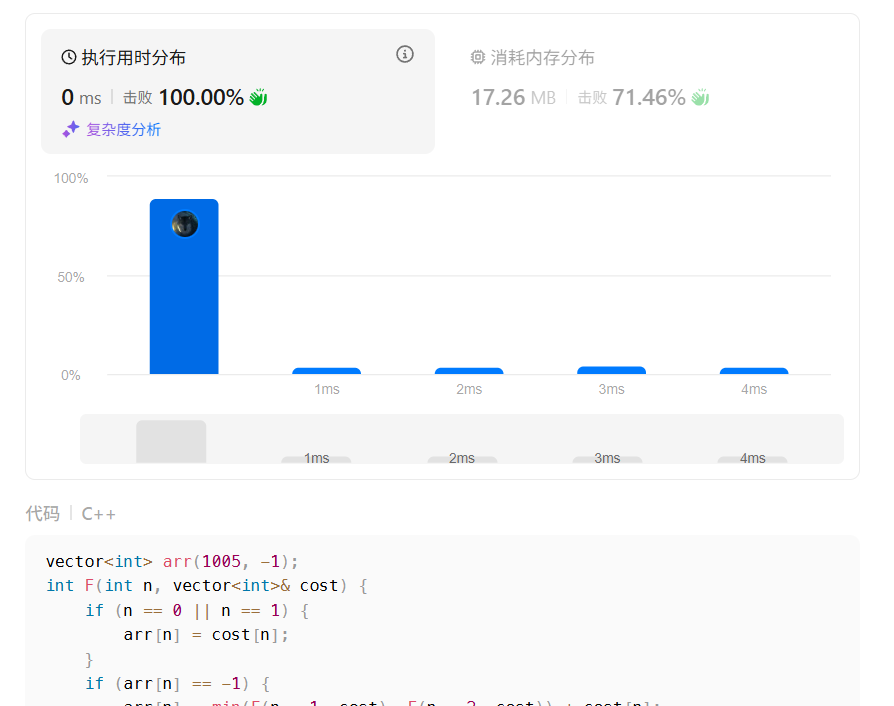

美化代码：

要保证幂等性，用全局变量就不合适，那就用局部变量呗

// 增加arr参数int F(int n, vector& cost, vector& arr) {    if (n == 0 || n == 1) {        arr[n] = cost[n];   }    if (arr[n] == -1) {        arr[n] = min(F(n - 1, cost, arr), F(n - 2, cost, arr)) + cost[n];   }    return arr[n];}​class Solution {public:    int minCostClimbingStairs(vector& cost) {        vector arr(cost.size(), -1);        return min(F(cost.size() - 1, cost, arr), F(cost.size() - 2, cost, arr));   }};

改迭代：

class Solution {public:    int minCostClimbingStairs(vector& cost) {        int dp[1005], n = cost.size();                dp[0] = cost[0];        dp[1] = cost[1];                for (int i = 2; i < n; ++i) {            dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];       }                return min(dp[n - 1], dp[n - 2]);   }};

现在是不是感觉迭代很简单，递归写的很复杂。但是递归是我们推出的关系最直接的表达，掌握熟练后直接写迭代即可，又快又简介。

官方题解：

class Solution {public:    int minCostClimbingStairs(vector& cost) {        int n = cost.size();        vector dp(n + 1);        dp[0] = dp[1] = 0;        for (int i = 2; i <= n; i++) {            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);       }        return dp[n];   }};​作者：力扣官方题解链接：https://leetcode.cn/problems/min-cost-climbing-stairs/solutions/528955/shi-yong-zui-xiao-hua-fei-pa-lou-ti-by-l-ncf8/来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Solution {public:    int minCostClimbingStairs(vector& cost) {        int n = cost.size();        int prev = 0, curr = 0;        for (int i = 2; i <= n; i++) {            int next = min(curr + cost[i - 1], prev + cost[i - 2]);            prev = curr;            curr = next;       }        return curr;   }};​作者：力扣官方题解链接：https://leetcode.cn/problems/min-cost-climbing-stairs/solutions/528955/shi-yong-zui-xiao-hua-fei-pa-lou-ti-by-l-ncf8/来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。