《C++二叉树进阶面试题整理+原理剖析》

前引：你是否在刷算法题时遇到过这样的场景？面对一组无序数据，需要频繁地查找某个特定值，或是动态插入新元素却不想每次都遍历全量数据；又或者在准备面试时，被面试官追问：\"如果用二叉树优化查找效率，应该怎么设计？\"——这时候，​搜索二叉树（Binary Search Tree, BST）​​ 往往会是解题的关键线索。作为数据结构中最经典的\"有序树\"代表，搜索二叉树的核心魅力在于：它通过左子树所有节点值小于根节点、右子树所有节点值大于根节点的天然有序性，将普通的二叉树升级为\"会排序的工具\"！

目录

【一】根据二叉树创建字符串

（1）题目链接

（2）思路讲解

（3）代码展示

【二】二叉树的层序遍历

（1）题目链接 

（2）思路讲解

（3）代码展示

【三】二叉树的最近公共祖先

（1）题目链接

（2）思路讲解

（3）代码展示

【四】由前序中序遍历还原二叉树

（1）题目链接

（2）思路讲解

（3）代码展示

【五】二叉树转双向链表

（1）题目链接

（2）思路讲解

（3）代码展示

【一】根据二叉树创建字符串

（1）题目链接

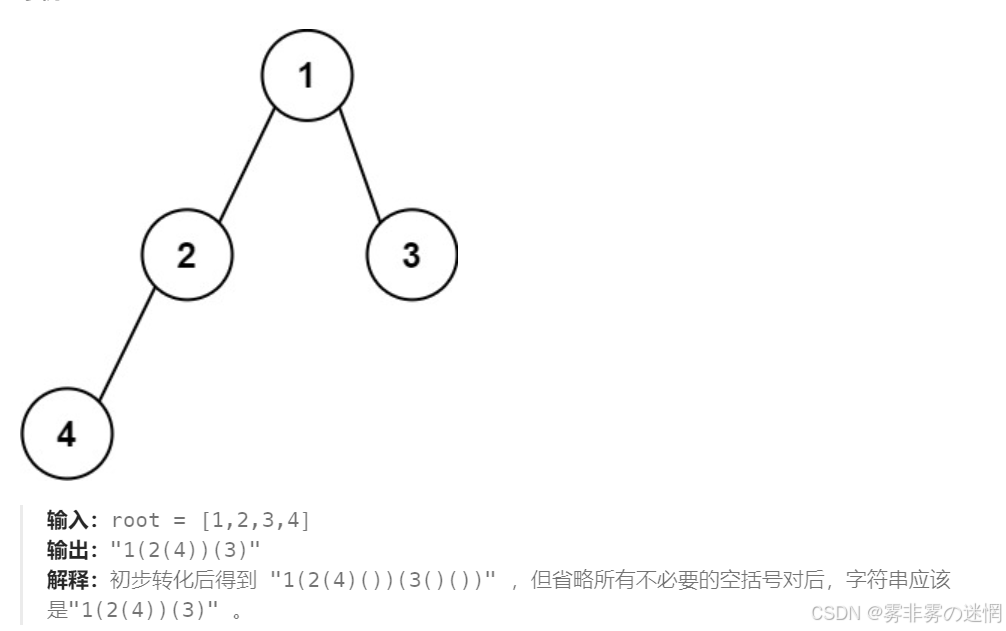
606. 根据二叉树创建字符串 - 力扣（LeetCode）606. 根据二叉树创建字符串 - 给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。空节点使用一对空括号对 \"()\" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。 示例 1：[https://assets.leetcode.com/uploads/2021/05/03/cons1-tree.jpg]输入：root = [1,2,3,4]输出：\"1(2(4))(3)\"解释：初步转化后得到 \"1(2(4)())(3()())\" ，但省略所有不必要的空括号对后，字符串应该是\"1(2(4))(3)\" 。示例 2：[https://assets.leetcode.com/uploads/2021/05/03/cons2-tree.jpg]输入：root = [1,2,3,null,4]输出：\"1(2()(4))(3)\"解释：和第一个示例类似，但是无法省略第一个空括号对，否则会破坏输入与输出一一映射的关系。 提示： * 树中节点的数目范围是 [1, 104] * -1000 <= Node.val <= 1000https://leetcode.cn/problems/construct-string-from-binary-tree

（2）思路讲解

首先我们看两个事例：

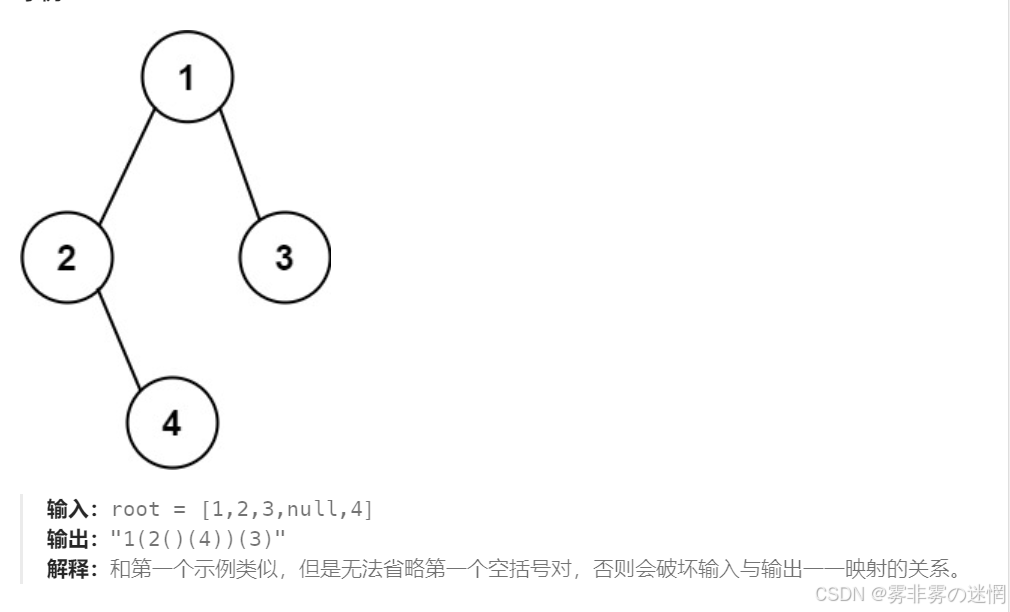
针对遍历结果，我们转化一下：

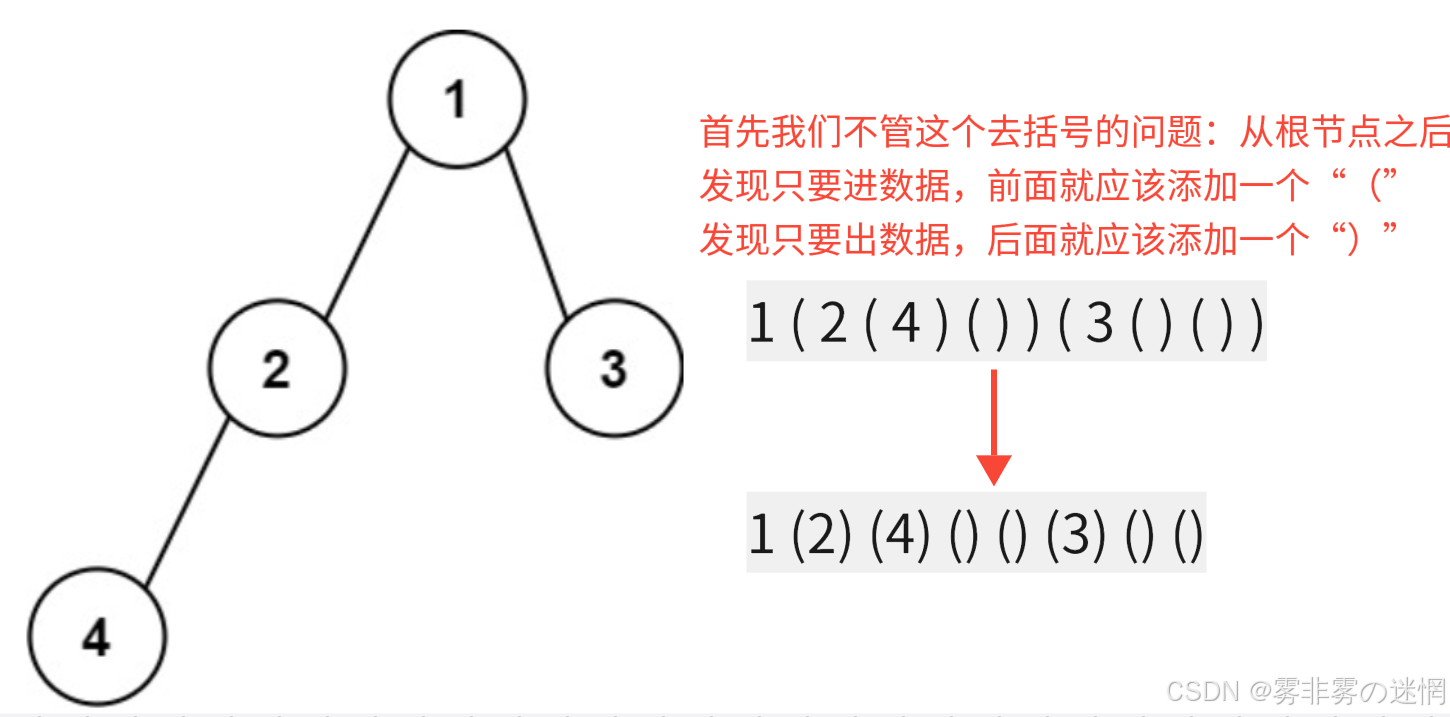我们可以写出代码：

 if(root==nullptr) { return string(); } string str; str += to_string(root->val); //左 str += \'(\'; str += tree2str(root->left); str += \')\'; //右 str += \'(\'; str += tree2str(root->right); str += \')\'; return str;

针对括号问题我们发现：

（1）左子节点为空，右子节点为空，都省去括号

（2）左子节点不为空，右子节点为空，省去右子节点的括号

（3）左子节点为空，右子节点不为空，保留右子节点括号

总结：

只要左边为空，那就判断右边；如果右边为空，那么右边的括号就可以不用存字符串

可以根据下面左右子节点的 if 条件来思考

（3）代码展示

class Solution {public: string tree2str(TreeNode* root) { if(root==nullptr) { return string(); } string str; str += to_string(root->val); if(root->left || root->right) { //左 str += \'(\'; str += tree2str(root->left); str += \')\'; } if(root->right) { //右 str += \'(\'; str += tree2str(root->right); str += \')\'; } return str; }};

【二】二叉树的层序遍历

（1）题目链接 

https://leetcode.cn/problems/binary-tree-level-order-traversalhttps://leetcode.cn/problems/binary-tree-level-order-traversal

（2）思路讲解

这题主要是层序遍历的实现：

层序遍历循环中，每一轮大循环遍历的是一层，那么我们需要把每层的数据先用一维数组存起来

一层结束之后最终再统一处理（例如：vector里面可以存数组）

（3）代码展示

// 层序遍历函数vector<vector> levelOrder(TreeNode* root){ //创建二维数组 vector<vector> result; if (root == nullptr) { return result; } queue q; q.push(root); //层序遍历 while (!q.empty()) { int levelSize = q.size(); //临时一维数组，用来存每层的数据 vector currentLevel; for (int i = 0; i val); if (node->left) q.push(node->left); if (node->right) q.push(node->right); } //二维数组存储一维数组 result.push_back(currentLevel); } return result;}

【三】二叉树的最近公共祖先

（1）题目链接

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-treehttps://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree

（2）思路讲解

首先我们先来理解最近的公共祖先：

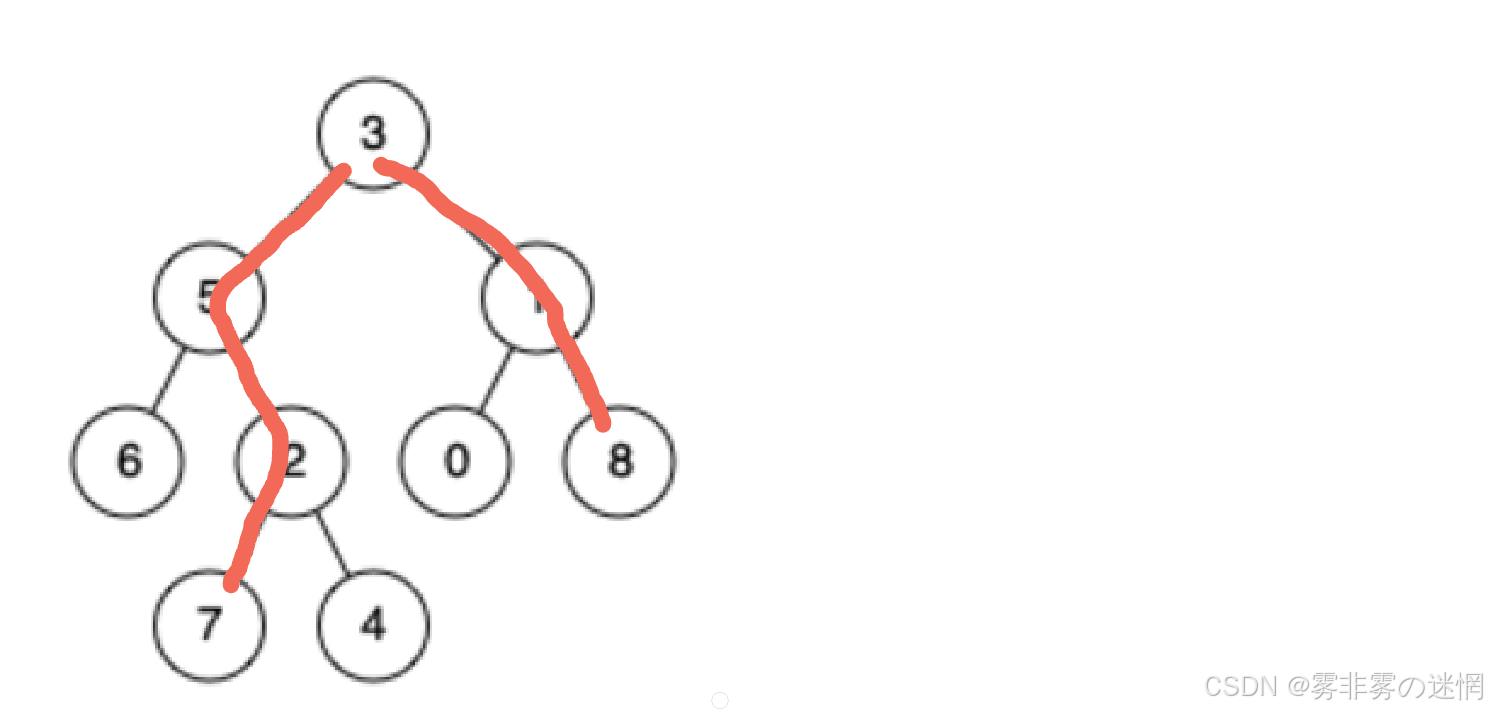
例如7和8的最近公共祖先是3

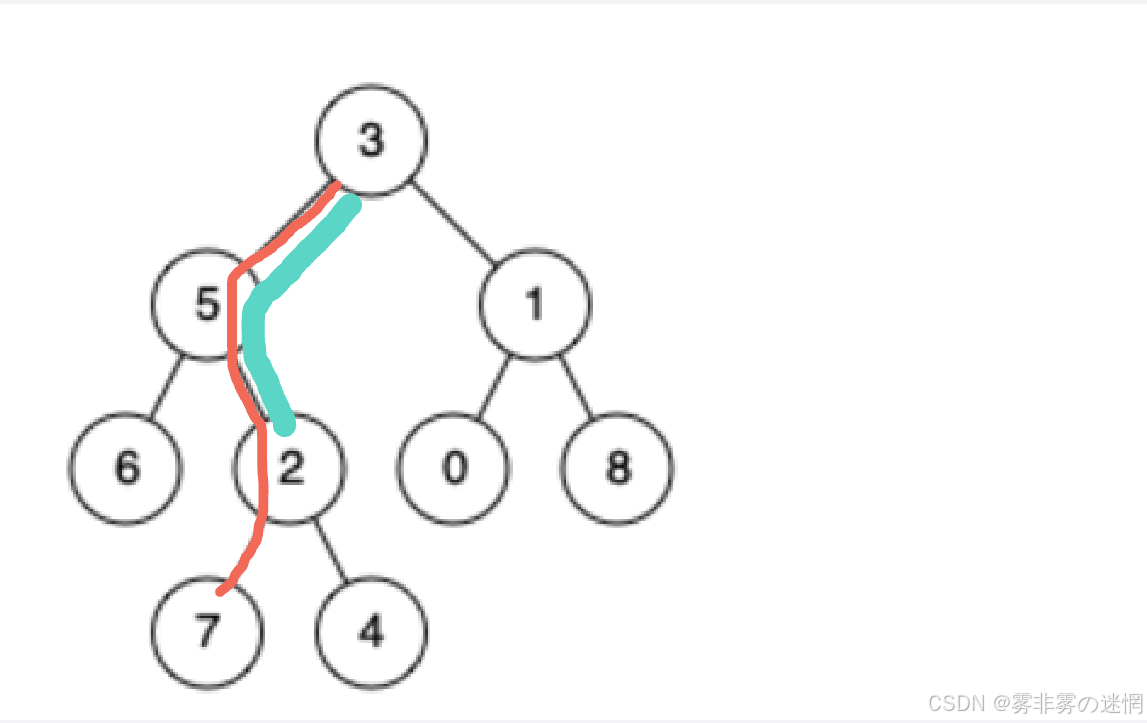
例如7和2的公共祖先是2（自己可以是自己的祖先）

下面我们来分析几种情况：

（1）如果两个节点在自己的左右子树，那么公共节点就是这个子树的根节点，例如：

（2）如果两个节点在自己的同一侧（左、右），我们可以继续递归查找

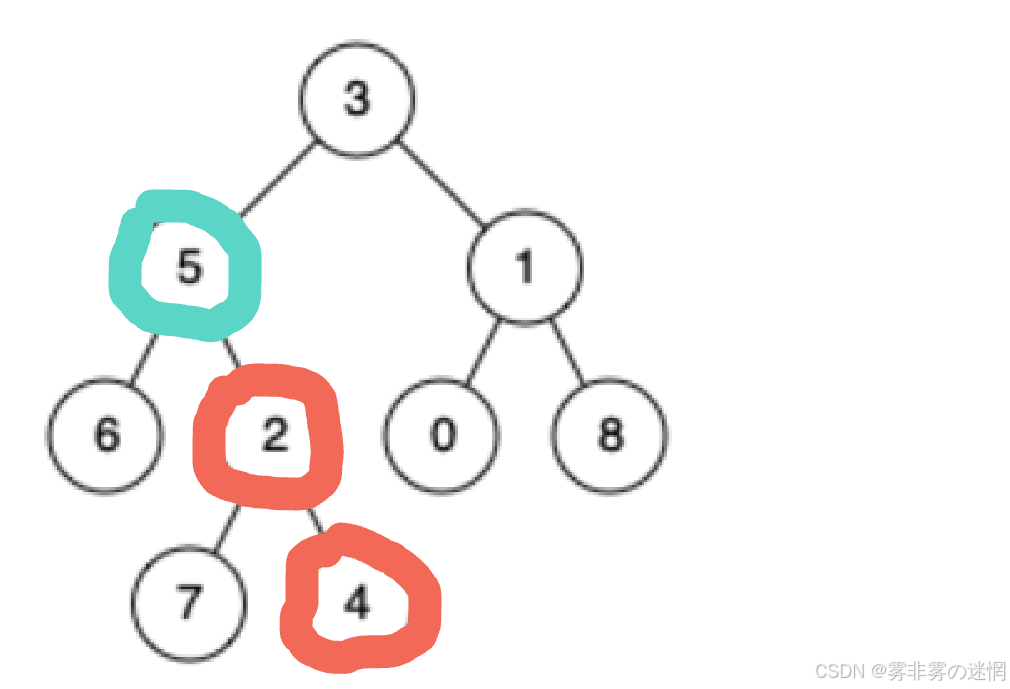
（3）如果自身就是某个节点，那么自己就是祖先节点

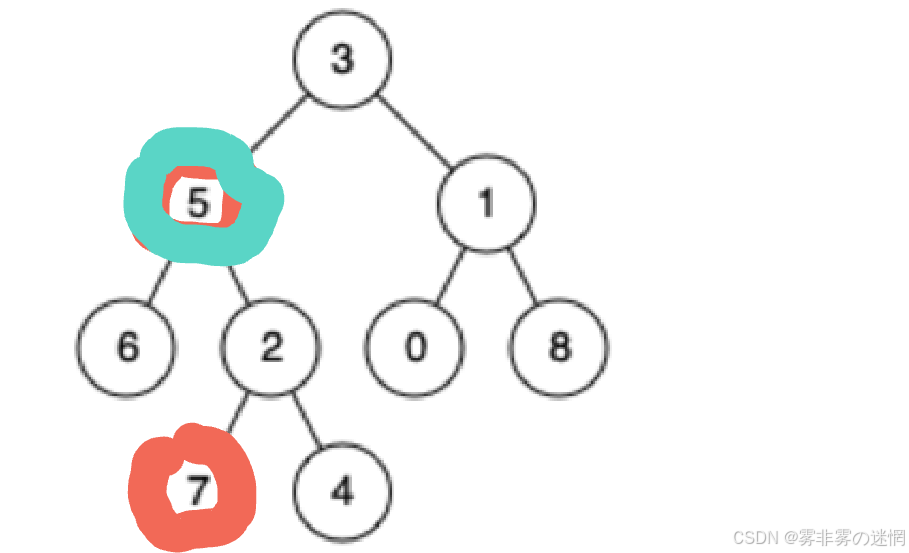
（3）代码展示

class Solution {public: //判断节点位置 bool Find(TreeNode* parent, TreeNode* target) { if (parent == nullptr) { return false; } if (parent->val == target->val) { return true; } return Find(parent->left, target) || Find(parent->right, target); } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { //第一种情况：如果自身就是目标节点 if(root==p||root==q) { return root; } //如果p在左，q在右 bool pfind=Find(root->left ,p); bool qfind =Find(root->right,q); //如果p在右，q在左 bool ppfind=Find(root->left,q); bool qqfind=Find(root->right,p); //第二种情况：如果在两侧 if(pfind && qfind || ppfind && qqfind) { return root; } else if(pfind && !qfind) { //如果都在左侧 return lowestCommonAncestor(root->left,p,q) ; } else if(!ppfind && qqfind) { //如果都在右侧 return lowestCommonAncestor(root->right,p,q) ; } return nullptr; }};

【四】由前序中序遍历还原二叉树

（1）题目链接

https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversalhttps://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal

（2）思路讲解

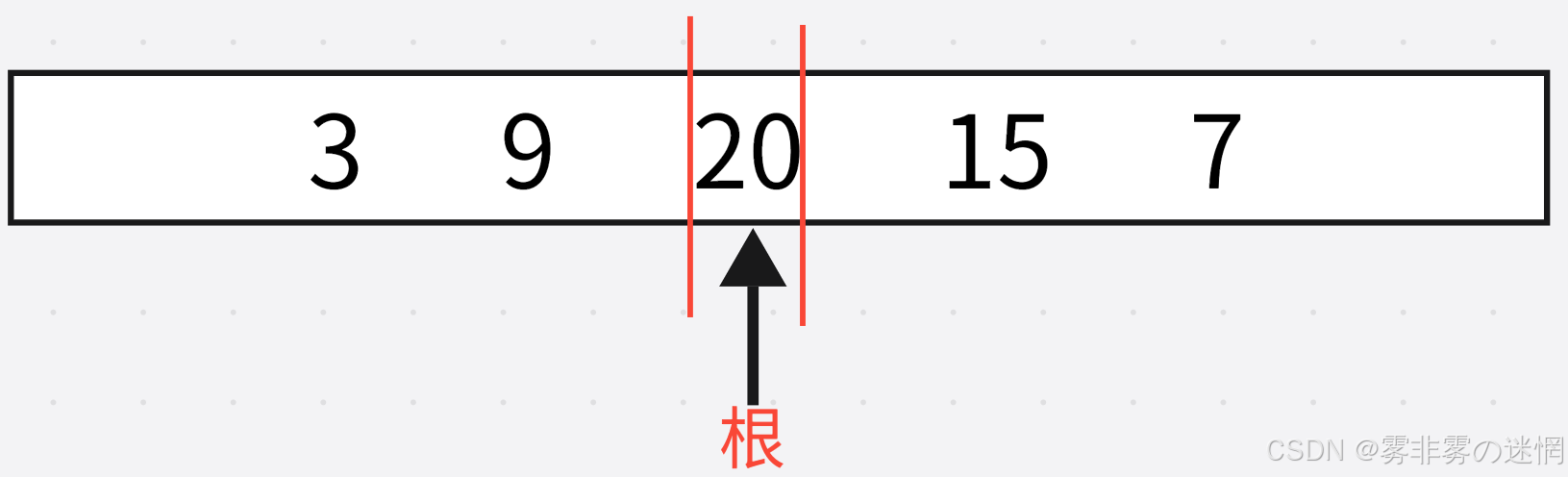
根据前序遍历：（根-左-右）我们可以确定第一个就是根节点

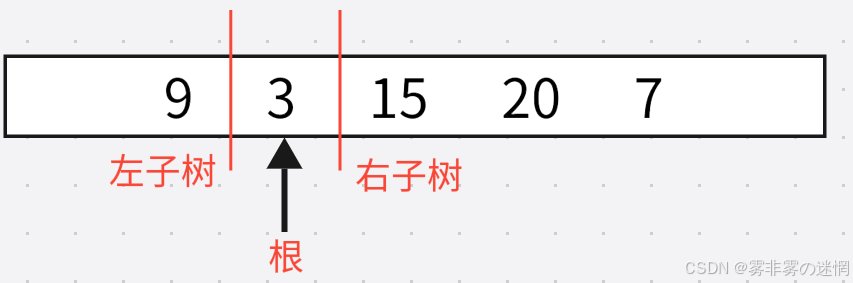
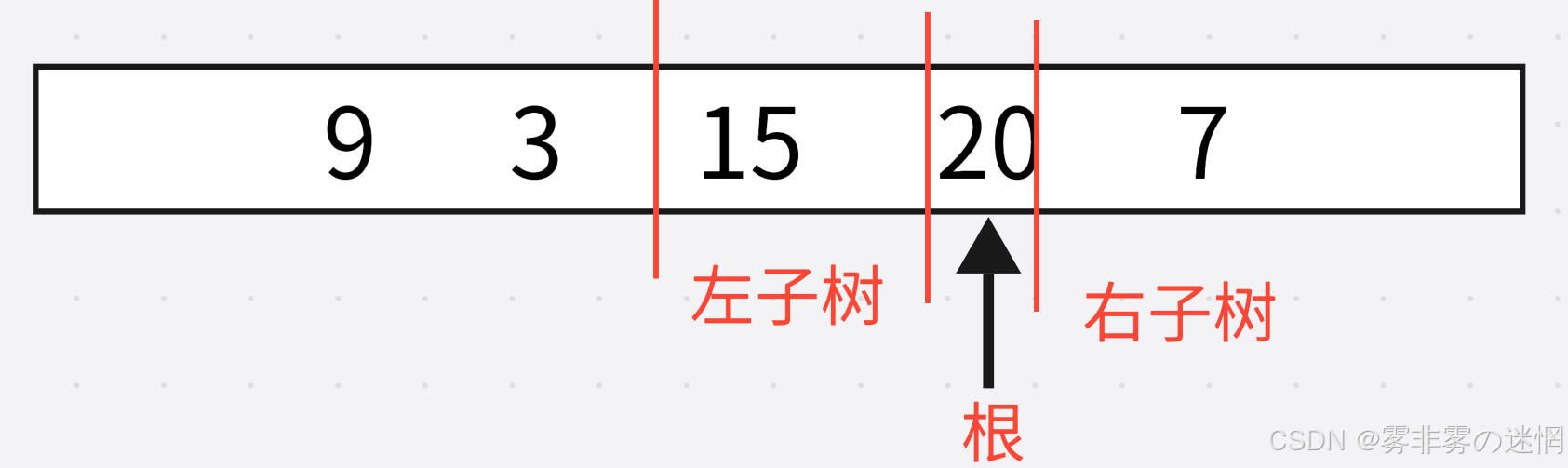
根据中序遍历：（左-根-右）我们可以根据根节点确定左右子树，例如：

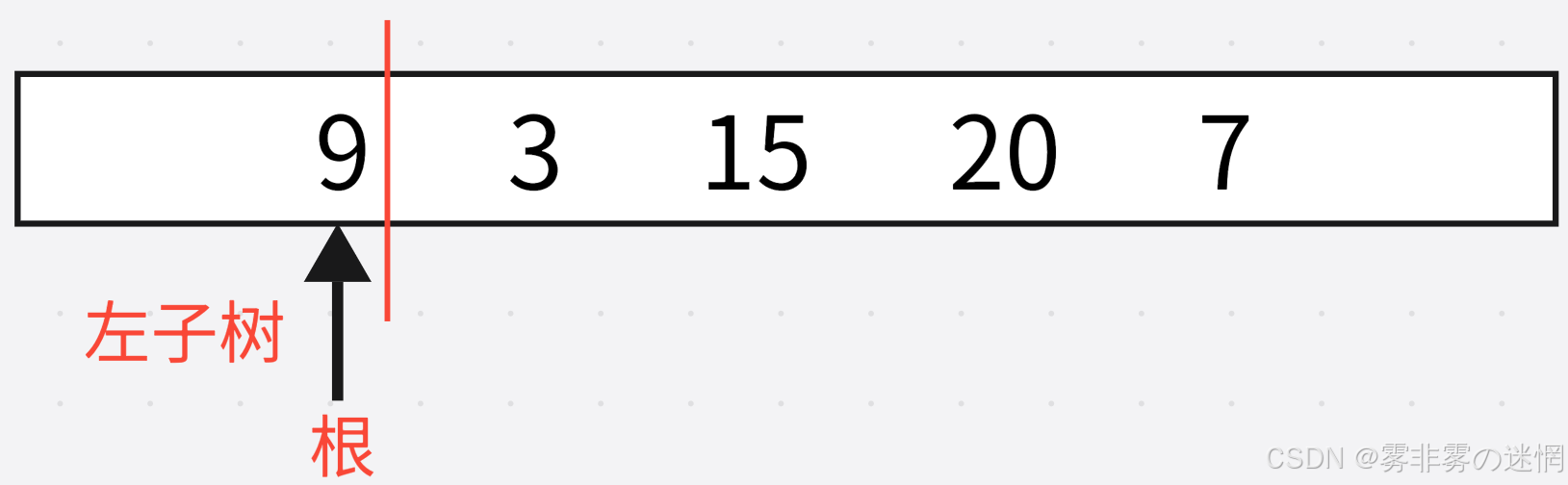
此时我们完成了第一轮递归，下面是第二轮递归：

下面是第三轮递归：

建议：画图理解，每次递归都需要控制区间 

注意：如果是由中序和后序还原二叉树，还是先找根->右子树->左子树

（3）代码展示

class Solution {public: TreeNode* build(vector& preorder,vector& inorder,int& prev,int begin,int end) { if(begin>end) { return nullptr; } //开辟父节点 TreeNode* node=new TreeNode(preorder[prev]); int rooti=begin; //找右区间 while(rootileft = build(preorder,inorder,prev,begin,rooti-1); //递归右子树 node->right = build(preorder,inorder,prev,rooti+1,end); return node; } TreeNode* buildTree(vector& preorder, vector& inorder) { int begin=0; int end=preorder.size()-1; int prev=0; return build(preorder,inorder,prev,begin,end); }};

【五】二叉树转双向链表

（1）题目链接

https://www.nowcoder.com/share/jump/1450133141752372969456https://www.nowcoder.com/share/jump/1450133141752372969456

（2）思路讲解

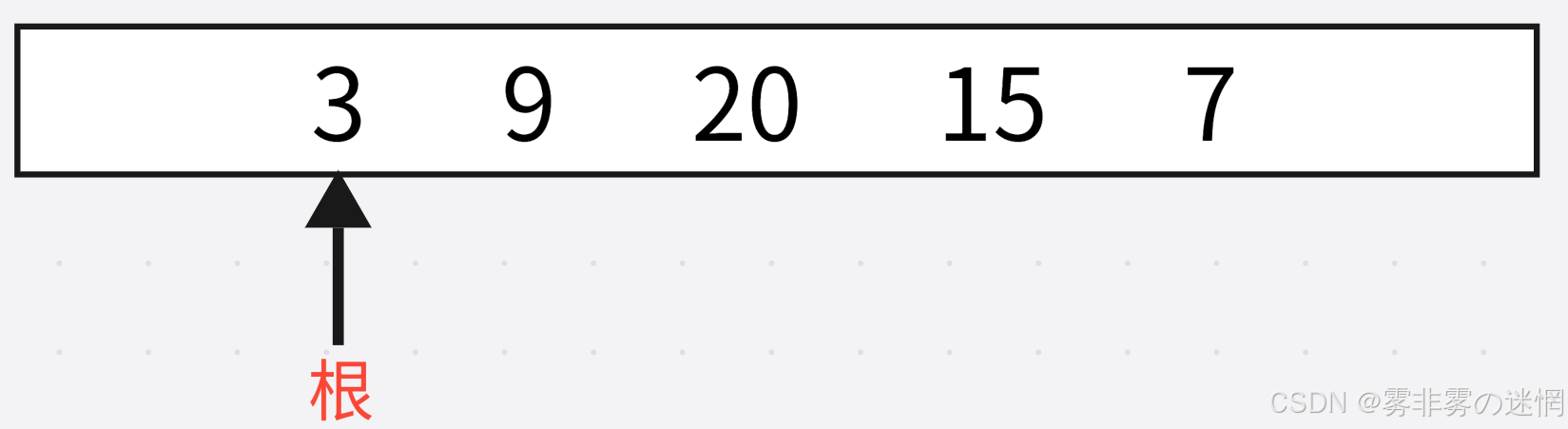
这题主要是改变左右指针的连接，执行连接操作的是中序遍历中的“根”，左右递归不用变

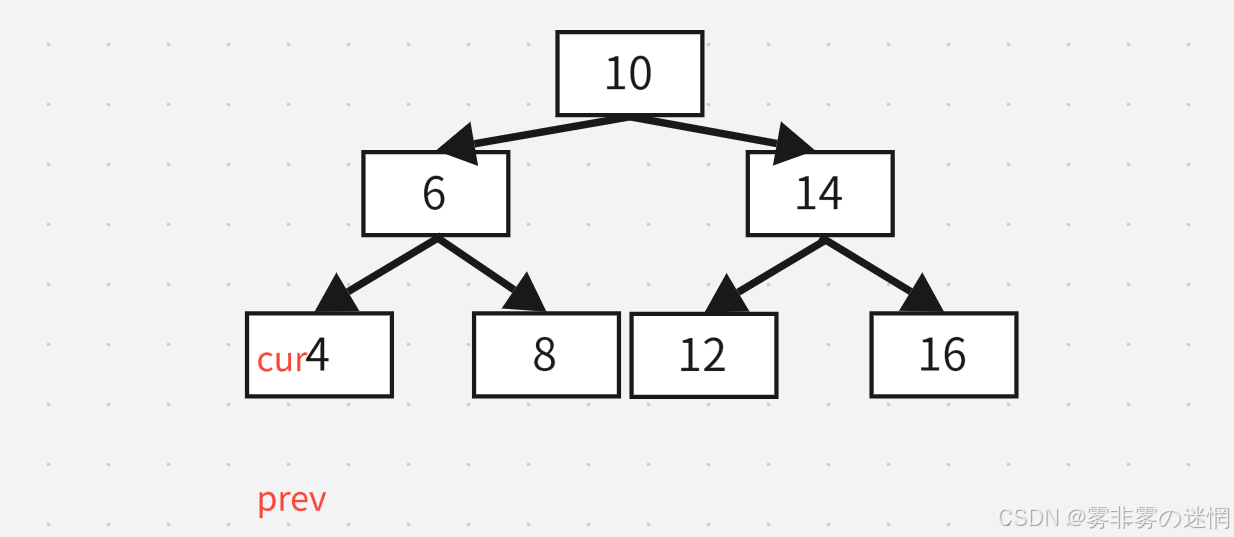
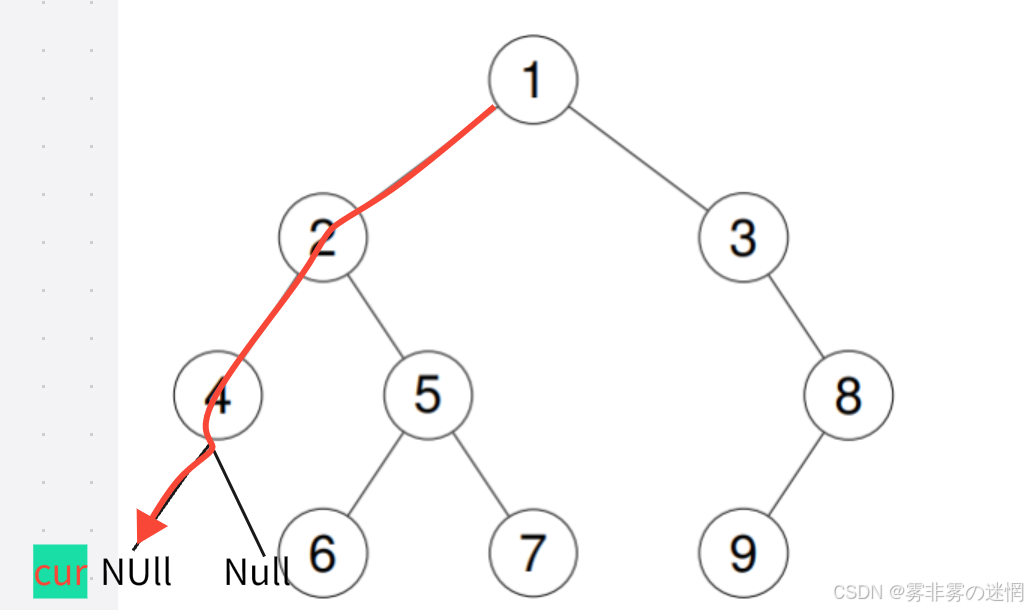
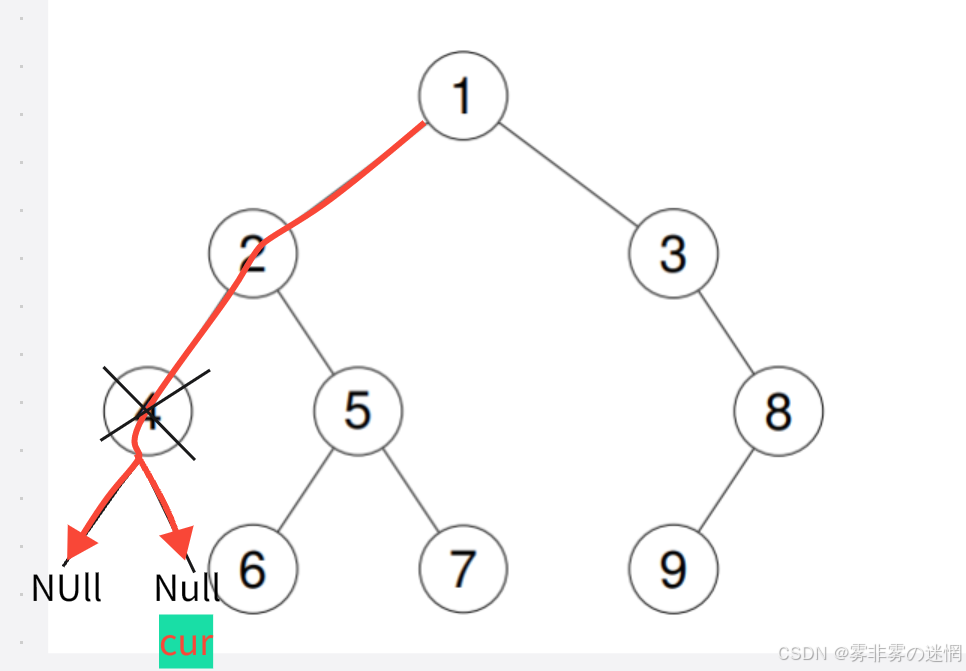
左：首先prev是空，cur经过中序遍历此时为4

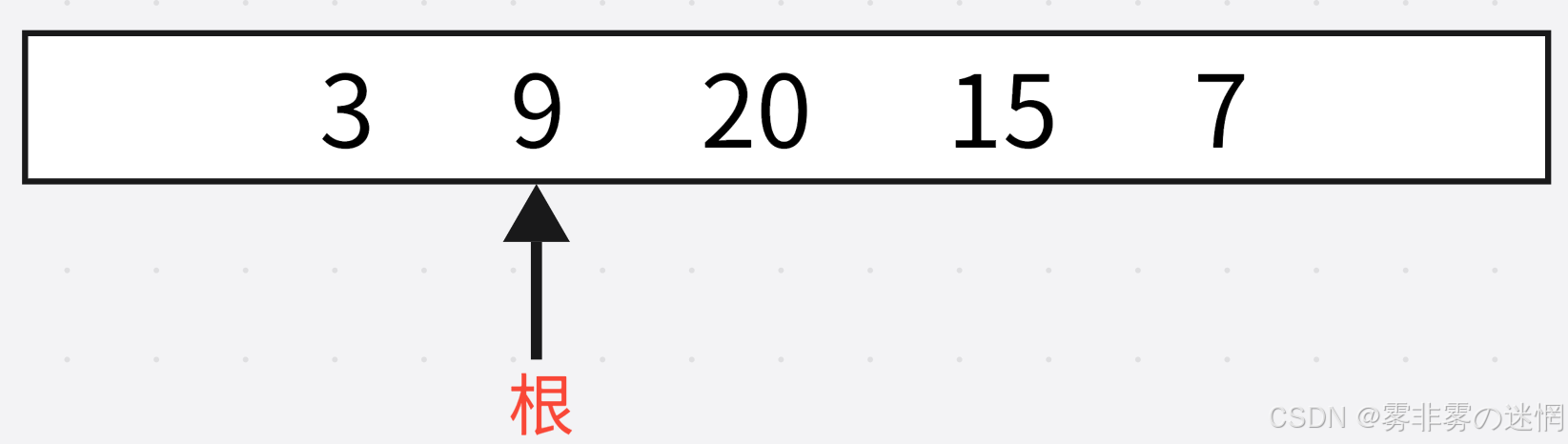
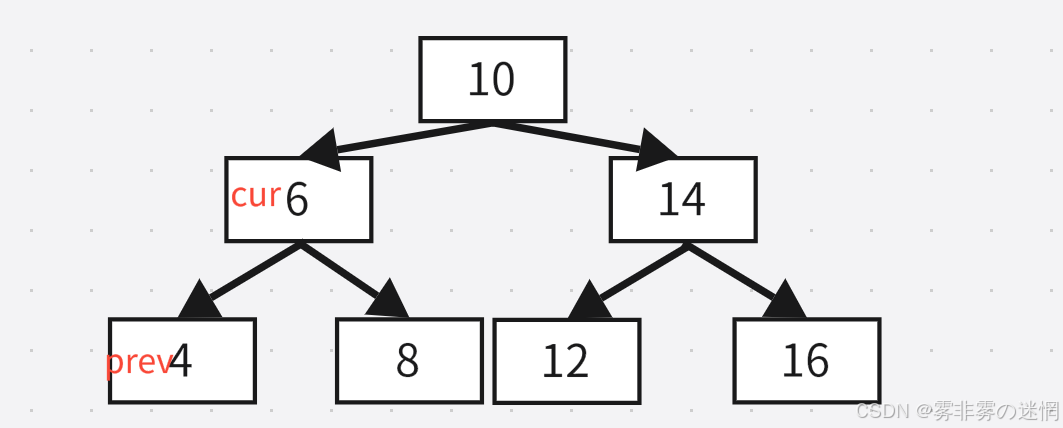
根：此时：cur是6，cur->left=prev我们就把prev换为cur，这样就完成了“prev”的连接

       同时：prev->right=cur；我们就完成了“next”的连接

       最后：我们改变prev即可，prev=cur，后面cur会随着递归自己遍历

注意：prev要用二级指针/引用，因为每个节点也是一个指针完成的

（3）代码展示

class Solution {public: void build(TreeNode* cur,TreeNode*& prev){if(cur==nullptr){return;}//左build(cur->left,prev);//连接prev(left)cur->left=prev;//连接next(right)if(prev){prev->right=cur;}prev = cur;//右build(cur->right,prev);} TreeNode* Convert(TreeNode* pRootOfTree) { TreeNode* prev=nullptr;build(pRootOfTree,prev);//找尾TreeNode* head = pRootOfTree;while(head && head->left){head=head->left;}return head; }};

【六】非递归实现前序遍历

（1）题目链接

https://leetcode.cn/problems/binary-tree-preorder-traversalhttps://leetcode.cn/problems/binary-tree-preorder-traversal

（2）思路讲解

前序遍历顺序：根->左->右

我们用循环把左路节点和它的值先入栈、存入vector，那么此时情况是这样的：

 //存储数组 vector V1; //创建栈存储左子树根节点 stack V2; TreeNode* cur=root; //所有左子树的根入栈 while(cur) { V1.push_back(cur->val); V2.push(cur); cur=cur->left; }

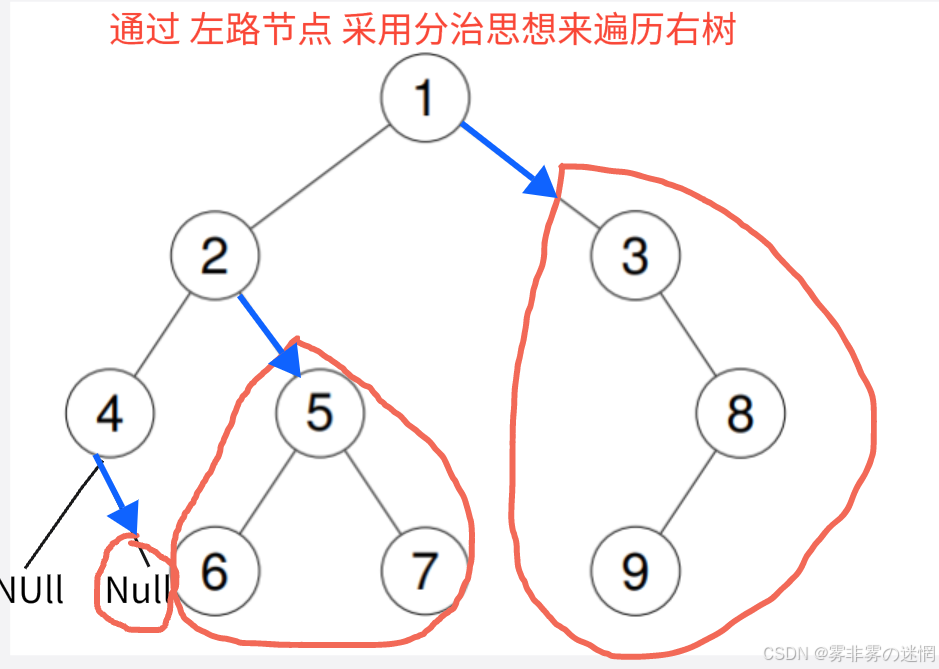
此时 cur 为空，但是 栈顶（4） 的右边可能还有值，我们应该让 cur 去 栈顶（4）的右边，再出栈，这样我们就回到了循环，将右子树用分治思想完成遍历

 //top为当前节点的右子树 TreeNode* top=V2.top(); V2.pop(); //跳到右子树 cur = top -> right;

整个循环的结束条件应该是：cur为空 或者 栈为空，则表示整棵树遍历完成

cur为空：可能cur的右子树还有它的子树，但是栈不为空，说明需要继续

·

总结：栈将左路节点全部入栈，通过栈顶元素的访问来不断调整右树的访问

（3）代码展示

class Solution {public: vector preorderTraversal(TreeNode* root) { if(root==nullptr) { return {}; } //遍历数组 vector V1; //创建栈存储左子树根节点 stack V2; TreeNode* cur=root; while(cur || !V2.empty()) { //所有左子树的根入栈 while(cur) { V1.push_back(cur->val); V2.push(cur); cur=cur->left; } //调整该节点的右树 TreeNode* top=V2.top(); //获取第二个栈顶元素 V2.pop(); //（精髓之处） cur = top-> right; } return V1; }};