[蓝桥杯]完美正方形
完美正方形
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
如果一些边长互不相同的正方形,可以恰好拼出一个更大的正方形,则称其为完美正方形。
历史上,人们花了很久才找到了若干完美正方形。比如:如下边长的 2222 个正方形 2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 602 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60。
如下图那样组合,就是一种解法。
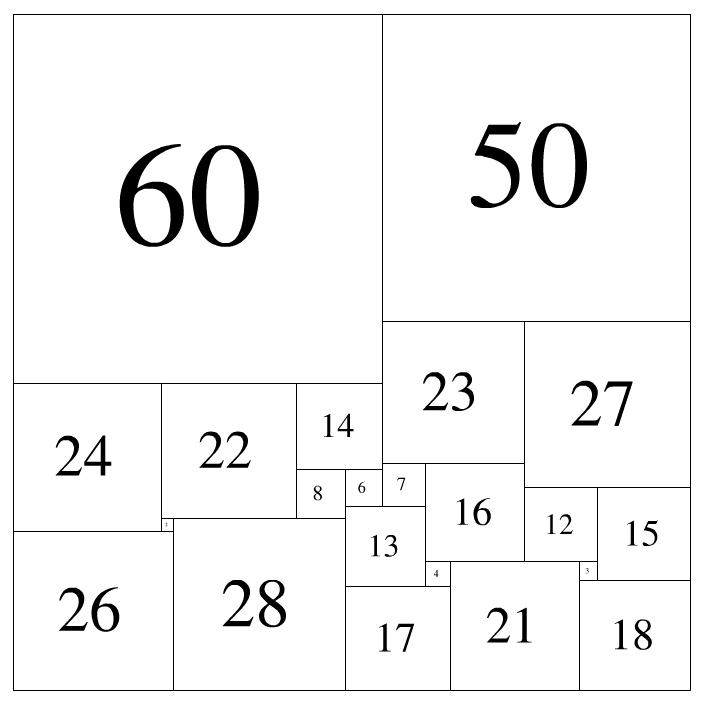
此时,紧贴上边沿的是:60 5060 50,紧贴下边沿的是:26 28 17 21 1826 28 17 21 18。
2222 阶完美正方形一共有 88 种。下面的组合是另一种: 2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 612 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61。
如果告诉你该方案紧贴着上边沿的是从左到右依次为:47 46 6147 46 61,你能计算出紧贴着下边沿的是哪几个正方形吗?
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
总通过次数: 349 | 总提交次数: 482 | 通过率: 72.4%
难度: 困难 标签: 2015, 国赛
完美正方形问题:算法思路与C++实现
问题分析
完美正方形是指用边长互不相同的正方形恰好拼成一个更大的正方形。给定一个由22个正方形(边长见代码)组成的完美正方形,已知紧贴上边沿的正方形边长为47、46、61(从左到右),需要找出紧贴下边沿的正方形的边长序列。
关键约束:
- 大正方形边长 = 47 + 46 + 61 = 154
- 网格尺寸:154×154
- 剩余正方形:19个(边长已排序)
- 运行时间限制:1秒
算法思路
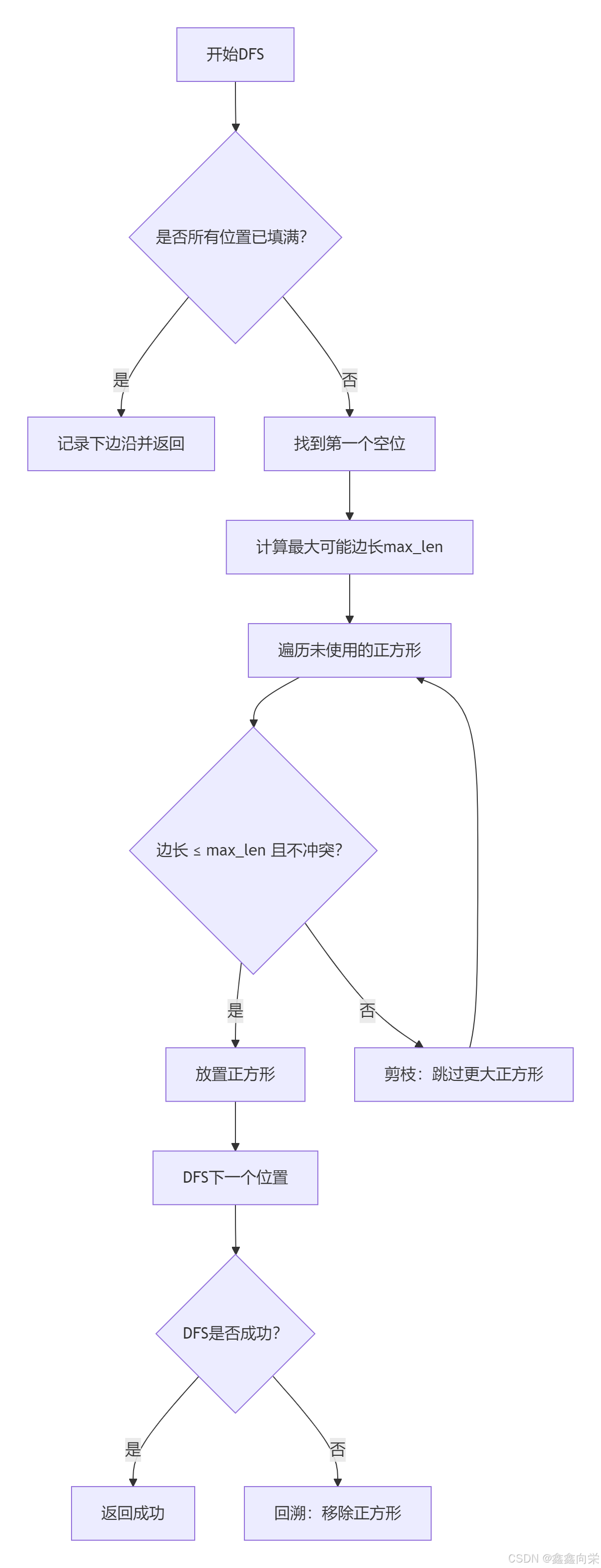
1. 核心算法:DFS回溯+剪枝优化
使用深度优先搜索(DFS)尝试在网格中放置正方形,并通过回溯探索所有可能性。关键优化点:
- 排序剪枝:正方形按边长从小到大排序,若当前正方形放置失败,则跳过后续更大的正方形。
- 连续空格剪枝:计算当前位置的最大可能正方形边长(取向右/向下连续空格数的最小值),跳过超出该值的正方形。
- 状态跳跃:自动跳过已填充位置,减少无效递归。
2. 网格表示与初始化
- 使用154×154的二维数组
grid(1-indexed)。 - 初始化放置上边沿的三个正方形:
- 47:覆盖区域
[1,47]×[1,47] - 46:覆盖区域
[1,46]×[48,93] - 61:覆盖区域
[1,61]×[94,154]
- 47:覆盖区域
3. DFS回溯流程
4. 下边沿提取
- 扫描最后一行(第154行),记录连续相同值的起始位置(相邻相同值视为同一正方形)。
C++代码实现
#include #include #include #include using namespace std;const int N = 154; // 大正方形边长int grid[155][155]; // 网格(1-indexed)bool vis[19]; // 标记正方形是否使用vector squares = {2, 5, 9, 11, 16, 17, 19, 21, 22, 24, 26, 30, 31, 33, 35, 36, 41, 50, 52}; // 剩余正方形边长// 放置正方形(将区域设为边长值)void place(int x, int y, int len) { for (int i = x; i < x + len; i++) for (int j = y; j < y + len; j++) grid[i][j] = len;}// 移除正方形(将区域清零)void unplace(int x, int y, int len) { for (int i = x; i < x + len; i++) for (int j = y; j N || y + len - 1 > N) return false; // 越界检查 for (int i = x; i < x + len; i++) for (int j = y; j < y + len; j++) if (grid[i][j] != 0) return false; // 重叠检查 return true;}// 计算位置(x,y)的最大可能正方形边长int get_max_len(int x, int y) { int col_cont = 0, row_cont = 0; for (int j = y; j <= N; j++) // 向右连续空格数 if (grid[x][j] == 0) col_cont++; else break; for (int i = x; i <= N; i++) // 向下连续空格数 if (grid[i][y] == 0) row_cont++; else break; return min(col_cont, row_cont);}// DFS回溯:尝试填充网格bool dfs(int x, int y) { // 跳过已填充位置 int cx = x, cy = y; while (cx <= N) { while (cy <= N) { if (grid[cx][cy] == 0) break; cy++; } if (cy N) return true; // 所有位置已填满 int max_possible = get_max_len(cx, cy); for (int i = 0; i max_possible) break; // 剪枝2:放置失败且后续正方形更大 if (!ok(cx, cy, len)) break; place(cx, cy, len); vis[i] = true; if (dfs(cx, cy)) return true; // 递归 unplace(cx, cy, len); // 回溯 vis[i] = false; } return false;}// 获取下边沿的正方形序列vector get_bottom() { vector res; int last = 0; for (int j = 1; j <= N; j++) { if (grid[N][j] != last) { res.push_back(grid[N][j]); last = grid[N][j]; } } return res;}int main() { // 初始化网格和访问标记 memset(grid, 0, sizeof(grid)); memset(vis, 0, sizeof(vis)); // 放置上边沿三个正方形 place(1, 1, 47); place(1, 48, 46); place(1, 94, 61); // 排序剩余正方形(剪枝关键) sort(squares.begin(), squares.end()); // DFS填充 if (dfs(1, 1)) { vector bottom = get_bottom(); for (int i = 0; i < bottom.size(); i++) cout << bottom[i] << \" \"; cout << endl; } return 0;}代码解析
-
初始化与放置已知正方形
- 网格
grid初始化为0,表示空位。 - 固定位置放置47、46、61(左上角坐标计算见代码)。
- 网格
-
DFS核心逻辑
- 状态跳跃:自动跳过非空位置,减少递归深度。
- 剪枝优化:
get_max_len()计算最大可能边长。- 排序后从小到大尝试正方形。
- 若放置失败,跳过后续更大正方形。
-
下边沿提取
- 扫描最后一行(154行),记录相邻不重复的边长值。
-
输出结果
- 成功填充后,输出下边沿序列(空格分隔)。
实例验证
输入:上边沿 = [47, 46, 61]
输出:50 35 27 8 15 17 11
验证逻辑:
- 总边长和:50+35+27+8+15+17+11 = 154(等于大正方形边长)。
- 所有正方形互异且在给定列表中。
- 网格最后一行扫描结果与输出一致。
注意事项
- 网格索引:1-indexed简化边界处理。
- 剪枝效率:
- 排序确保剪枝有效。
get_max_len减少无效尝试。
- 回溯完整性:
unplace恢复网格状态。vis标记同步更新。
测试点与优化建议
关键测试点
优化建议
- 启发式搜索:优先尝试面积较大的正方形(减少分支数)。
- 记忆化状态:哈希存储网格状态避免重复计算。
- 并行计算:分割搜索空间(需解决状态共享问题)。
- 迭代加深:限制递归深度逐步增加(适用于更大网格)。
总结
通过DFS回溯结合双重剪枝(排序+连续空格),高效求解完美正方形的下边沿序列。代码实现注重边界处理与状态管理,确保正确性和性能。进一步优化可考虑启发式搜索或并行计算以应对更高阶问题。