【动态规划 | 回文字串问题】动态规划解回文问题的核心套路

回文问题在面试中屡见不鲜，动态规划能高效解决这类问题。本文将直击核心，详解如何用DP快速判断子串是否回文：从状态定义到转移方程，再到遍历技巧，助你掌握解题精髓，轻松应对最长回文子串、回文分割等高频考题！

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\\ C++
🌈初/高阶数据结构专栏： 初阶数据结构\\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志 我自踏雪至山巅

文章目录

• • 647. 回文子串
  • 5. 最长回文子串
  • 1745. 分割回文串 IV
  • 132. 分割回文串 II
  • 516. 最长回文子序列
  • 1312. 让字符串成为回文串的最少插入次数

647. 回文子串

【题目】：647. 回文子串

【算法思路】

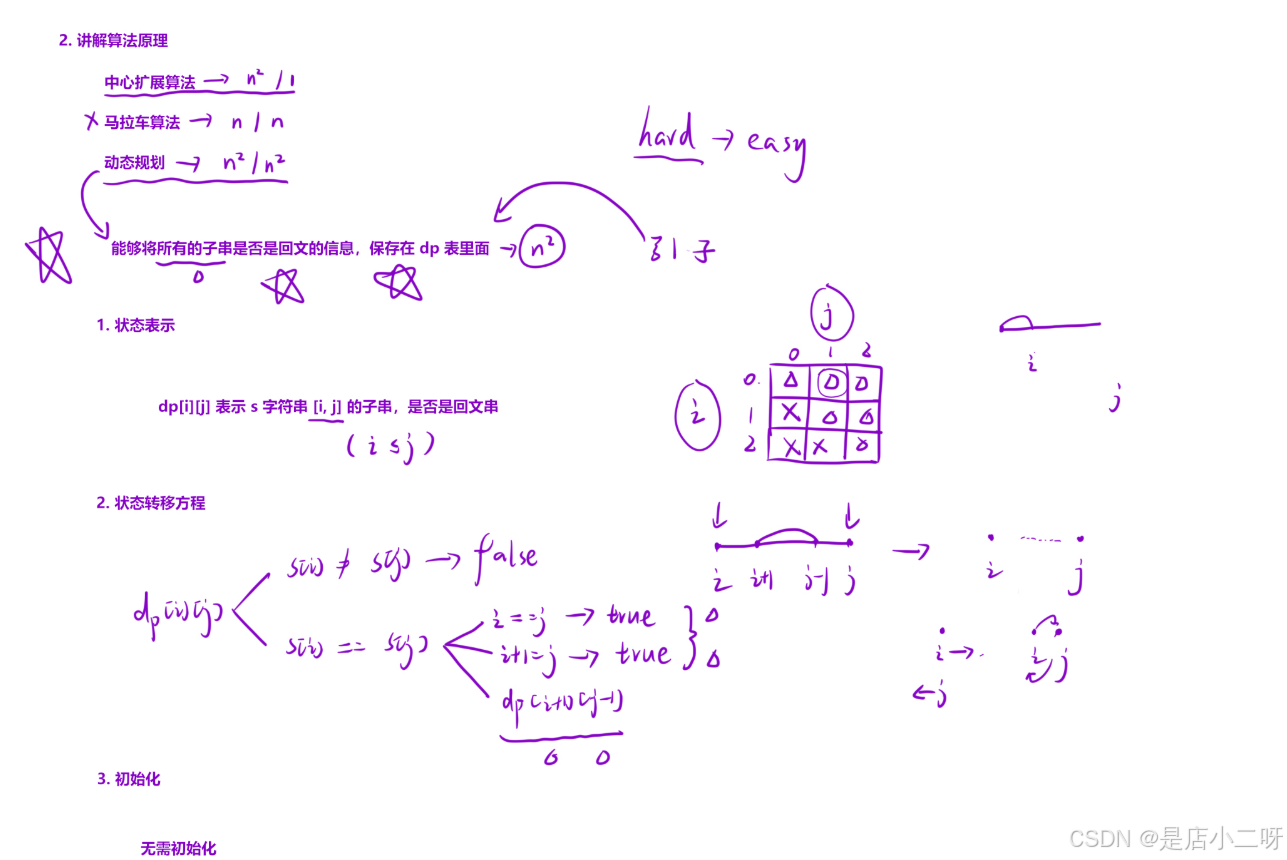
在回文串相关问题中，通常有三种常见的解决方法：中心扩展算法、马拉车算法和动态规划算法。在本系列中，我们采用动态规划来解决“回文数”这一类问题。

通过动态规划，可以有效地将原本较难的“回文数”问题转化为较简单的问题。关键在于\"将所有子串是否为回文的信息保存在一个 dp 表中\"。

这里不能简单地依赖“经验 + 题目要求”来直接定义状态表示，因为无法仅通过前部分和前一个元素的回文状态来推导后续状态。对于回文串问题，更合适的方法是从两侧入手，通过状态表示来建立状态转移方程，逐步判断子串是否为回文

在动态规划中，dp[i][j] 表示字符串 s[i, j] 是否为回文串。我们需要分析两种情况：一是两侧字符相等，二是两侧字符不等。如果两侧字符相等，则可以进一步细分为不同的状态进行分析。

关于初始化，通过矩阵图和状态转移方程的分析，我们可以得出状态转移是从下往上的。

这样，动态规划通过构建 dp 表，能够从小规模的子问题逐步解决整个问题，最终判断整个字符串是否为回文串。同时，i <= j 的条件避免了出现 j > i 的情况，因此无需额外的初始化操作。

通过矩阵分析，每个表格对应一个区间，表示不同区间的子串。动态规划优化了暴力搜索的过程，通过逐步计算并记录子串的回文信息，避免了重复计算

【代码实现】

class Solution {public: int countSubstrings(string s) { //1.创建dp表 int n = s.size(); vector<vector<bool>> dp(n, vector<bool>(n)); //2.填表 int ret = 0; for(int i = n - 1; i >= 0; i--) { for(int j = i; j < n; j++) { if(s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true; if(dp[i][j] == true) ret++; } } //3.返回值 return ret; }};

5. 最长回文子串

【题目】：5. 最长回文子串

【算法思路】

首先，我们需要判断子串是否是回文。这时，我们可以利用‘通过 dp 表统计所有子串是否为回文’的技巧，从 dp 表的起始位置获取我们需要的结果。

根据‘经验 + 题目要求’，状态表示为 s[i, j] 是否为回文串。如果需要返回最长回文串，可以引入变量 begin 和 len 来进行记录和判断。初始化时，依据矩阵分析和状态转移方程，状态填表应从下往上进行。

当 s[i] == s[j] 时，可以通过分析三种情况来更新 dp[i][j]，具体为：dp[i][j] = (i + 1 < j) ? dp[i + 1][j - 1] : true;

【代码实现】

class Solution {public: string longestPalindrome(string s) { //1.创建dp表 int n = s.size(); vector<vector<bool>> dp(n, vector<bool>(n)); //2.填表操作 int len = 0; int begin = 0; for(int i = n - 1; i >= 0; i--) { for(int j = i; j < n; j++) { if(s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true; if(dp[i][j] == true && len < j - i + 1) {  len = j - i + 1;  begin = i; } } } //3.返回值 return s.substr(begin, len); }};

1745. 分割回文串 IV

【题目】：1745. 分割回文串 IV

【算法思路】

还记得那个小技巧——‘通过 dp 表统计所有子串是否为回文’吗？最后，使用两个 for 循环来遍历，确保满足条件 if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1]) return true;。在这里，需要注意 for 循环参数的填写细节，确保正确地遍历所有可能的子串区间。

【代码实现】

class Solution {public: bool checkPartitioning(string s) { //1.创建dp表 int n = s.size(); vector<vector<bool>> dp(n, vector<bool>(n)); //2.填表 for(int i = n - 1; i >= 0; i--) { for(int j = i; j < n; j++) { if(s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true; }  } //3.全部枚举判断 for(int i = 1; i < n; i++) { for(int j = i; j < n - 1; j++) { if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1]) return true; } } return false; }};

132. 分割回文串 II

【题目】：132. 分割回文串 II

【算法思路】

根据经验和题目要求，我们可以得到状态表示。具体来说，可以选择以[i, j]的范围来表示状态，也可以选择以i位置为结尾来表示状态。由于问题要求最小分割次数，因此更适合选择以i位置为结尾的方式来进行状态表示

通过绘图分析，我们可以聚焦于i位置的情况。只要i位置满足最长回文子串，则分割次数为0。需要结合之前的状态来进行分析，得到状态转移方程。如果[0, i]不是回文串，则需要进行前置分割；当[j, i]是回文串时，我们将状态传递给[0, j]，并根据[0, j]是否为回文串来确定状态转移，从而形成完整的状态转移方程。这里为了不影响max函数，位置默认初始化为最大值。

判断回文串时需要不断遍历，时间复杂度较高。为了解决这个问题，我们可以将回文串的信息存储在dp表中，从而优化代码的效率。

【代码实现】

class Solution {public: int minCut(string s) { //1.是否回文串 int n = s.size(); vector<vector<bool>> isPal(n, vector<bool>(n)); for(int i = n - 1; i >= 0; i--) for(int j = i; j < n; j++) if(s[i] == s[j]) isPal[i][j] = i+ 1 < j ? isPal[i + 1][j - 1] : true; //2.创建dp表 vector<int> dp(n, INT_MAX); //3.填表操作 for(int i = 0; i < n; i++) { if(isPal[0][i]) dp[i] = 0; else { for(int j = 1; j <= i; j++) if(isPal[j][i]) dp[i] = min(dp[j - 1] + 1, dp[i]); } } //4.返回值 return dp[n - 1]; }};

516. 最长回文子序列

【题目】：516. 最长回文子序列

【算法思路】

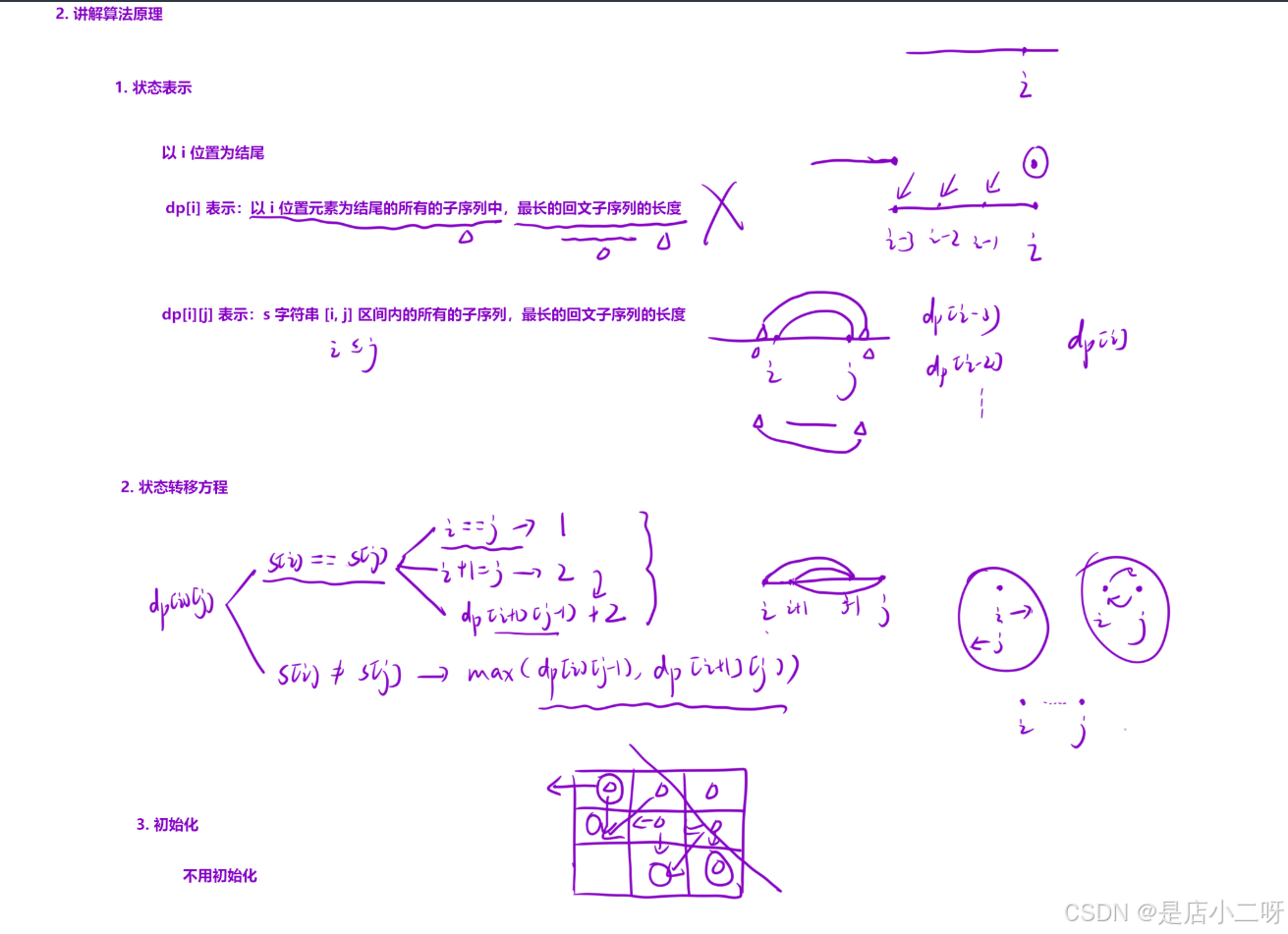
一开始考虑根据‘经验 + 题目要求’，以i位置元素为结尾来得到状态表示。但问题在于，若i位置之前是回文串，加入i位置元素后，是否依然是回文串并不确定。因此，无法直接得到状态转移方程。

如果这种‘经验’不可行，我们可以尝试其他的策略，比如考虑s字符串的[i, j]区间。这也是一种经验，根据当前状态标识，这个区间表示的是最长回文子序列。接下来，我们需要根据最近一次的状态，通过它们之间的关系推导出状态转移方程。根据矩阵分析，我们可以直接合并状态，而无需单独初始化。

【代码实现】

class Solution {public: int longestPalindromeSubseq(string s) { //1.小技巧 int n = s.size(); vector<vector<bool>> isPal(n, vector<bool>(n)); for(int i = n - 1; i >= 0; i--) for(int j = i; j < n; j++) if(s[i] == s[j])  isPal[i][j] = i + 1 < j ? isPal[i + 1][j - 1] : true; //2.创建dp表 vector<vector<int>> dp(n, vector<int>(n)); //3.填表操作 for(int i = n - 1; i >= 0; i--) { for(int j = i; j < n; j++) { if(s[i] != s[j]) dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]); else dp[i][j] = j == i ? 1 : dp[i + 1][j - 1] +2; } } //4.返回值 return dp[0][n - 1]; }};

1312. 让字符串成为回文串的最少插入次数

【题目】：1312. 让字符串成为回文串的最少插入次数

【算法思路】

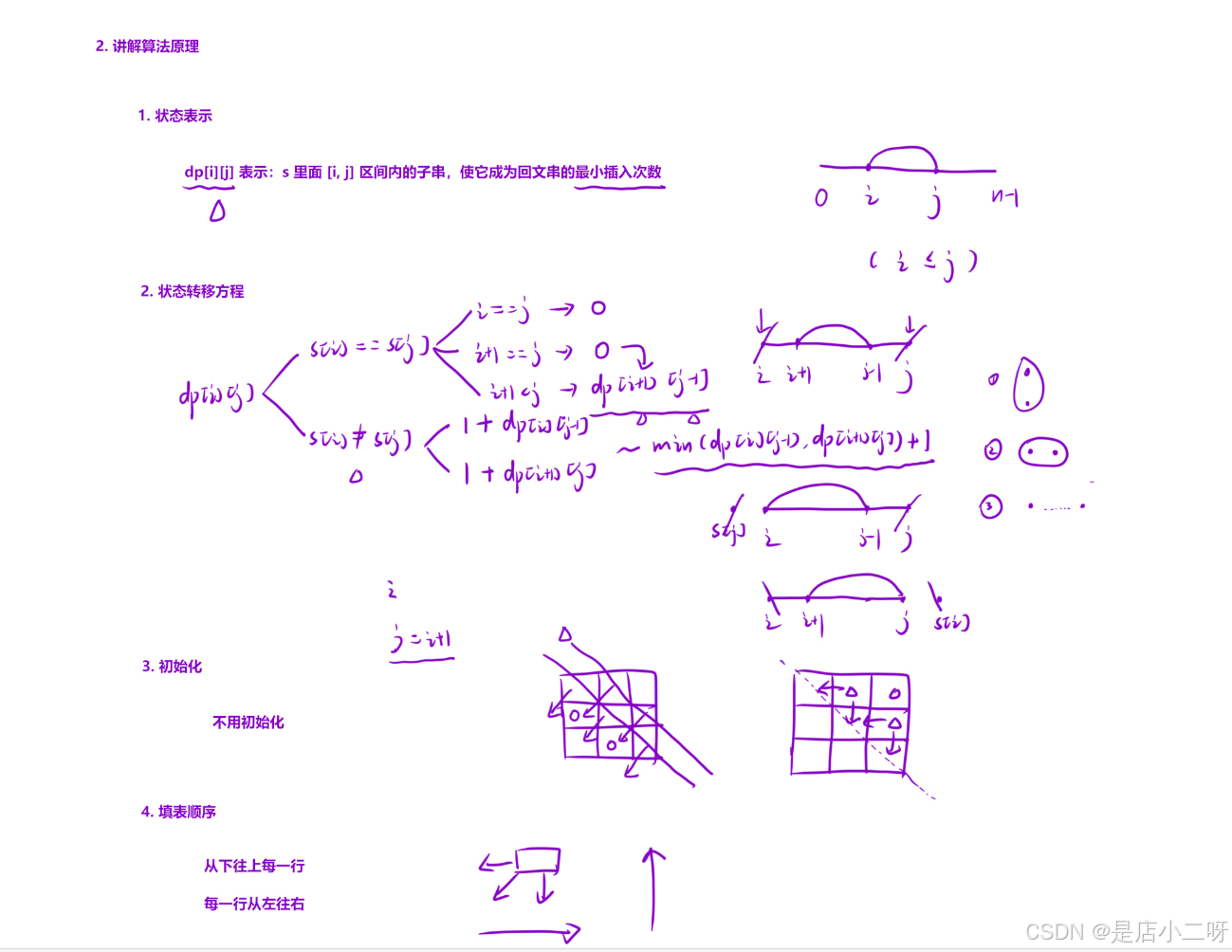
根据‘经验 + 题目要求’，我们需要确定状态表示，即在s的[i, j]区间内，使其成为回文串所需的最小插入次数。这里可以通过绘图分析具体情况。对于s[i] == s[j]，可以分为两种情况：如果相等，则无需插入，直接向最近一次状态转移；如果不相等，则需要进一步分析，可以选择i前进一步或j后退一步进行递归处理。

在填表时，我们需要从下往上遍历每一行，并在每一行中从左往右更新状态，无需额外初始化。

【代码实现】

class Solution {public: int minInsertions(string s) { //1.创建dp表 int n = s.size(); vector<vector<int>> dp(n, vector<int>(n)); //2.填表操作 for(int i = n - 1; i >= 0; i--) { for(int j = i + 1; j < n; j++)//i == j一定相等。 { if(s[i] == s[j]) dp[i][j] =dp[i + 1][j - 1]; else dp[i][j] = min(dp[i][j - 1], dp[i + 1][j]) + 1; } } //3.返回值 return dp[0][n - 1]; }};

快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！

清水丽人化妆品