神经网络激活函数：从ReLU到前沿SwiGLU

技术文档

摘要

本文全面介绍了神经网络中常用的激活函数，包括Sigmoid、Tanh、ReLU等传统函数，以及2017年后出现的Swish、Mish、SwiGLU等新兴函数。每个函数均提供数学定义、优缺点分析、Python实现代码和可视化图像，并附有实际应用建议和性能对比数据，帮助读者根据具体任务选择合适的激活函数。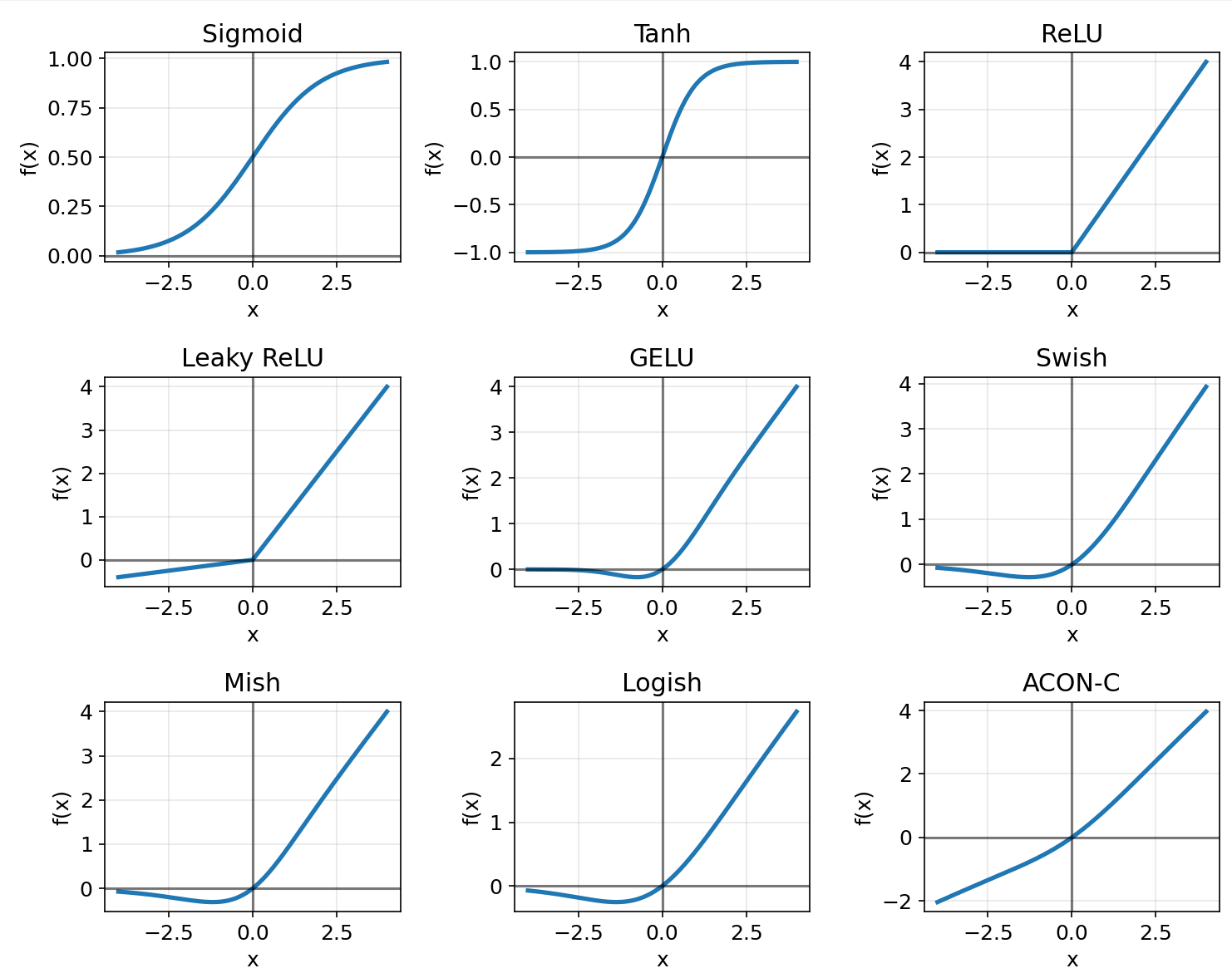
神经网络激活函数：从ReLU到前沿SwiGLU

1. 激活函数核心概念与作用

激活函数是神经网络中的非线性变换组件，其主要作用包括：

引入非线性：使神经网络能够学习复杂模式和关系
控制输出范围：限制神经元输出值在合理范围内
影响梯度流动：通过导数影响反向传播中的梯度计算
增强表示能力：提高模型对复杂数据的拟合能力

理想激活函数的特性：

非线性
可微分（至少几乎处处可微）
单调性（多数但不必须）
近似恒等性（f(x)≈x near 0）

2. 传统激活函数

2.1 Sigmoid

数学定义： $\\frac{1}{1 + e^{-x}}$
优点：输出范围(0,1)，平滑可微，适合概率输出
缺点：梯度消失严重，输出非零中心，指数计算成本高
适用场景：二分类输出层，LSTM门控机制

def sigmoid(x): return 1 / (1 + np.exp(-x))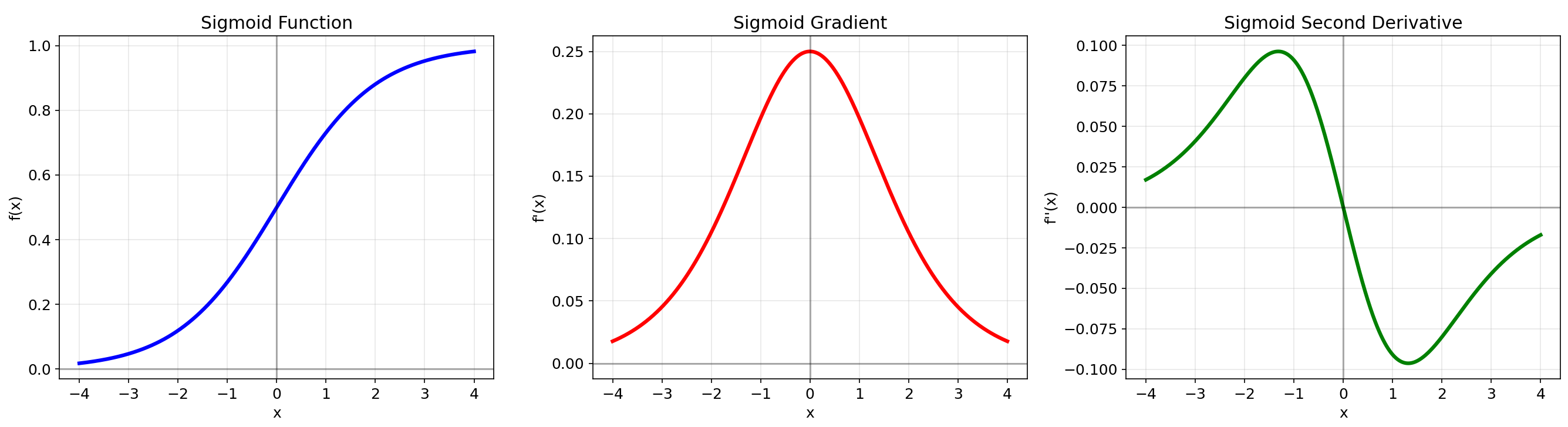

神经网络激活函数：从ReLU到前沿SwiGLU

2.2 Tanh

数学定义： $\\frac{e^x - e^{-x}}{e^x + e^{-x}}$
优点：输出范围(-1,1)，零中心化，梯度强于Sigmoid
缺点：梯度消失问题仍然存在
适用场景：RNN隐藏层

def tanh(x): return np.tanh(x)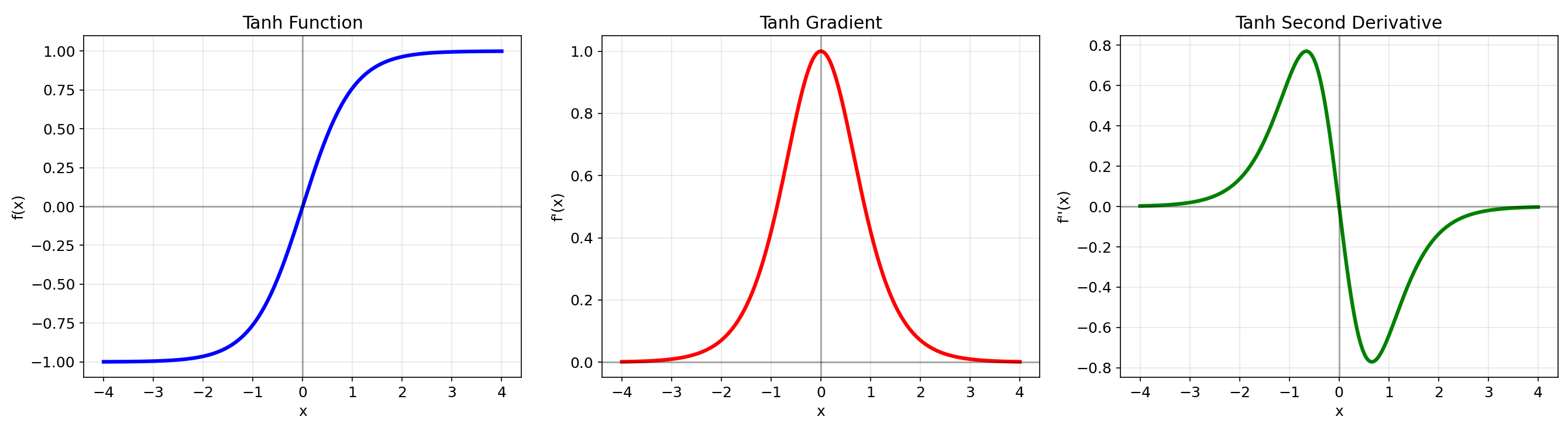

神经网络激活函数：从ReLU到前沿SwiGLU

2.3 ReLU (Rectified Linear Unit)

数学定义： $\\max(0, x)$
优点：计算高效，缓解梯度消失，稀疏激活
缺点：神经元死亡问题，输出非零中心化
适用场景：CNN隐藏层（默认选择）

def relu(x): return np.maximum(0, x)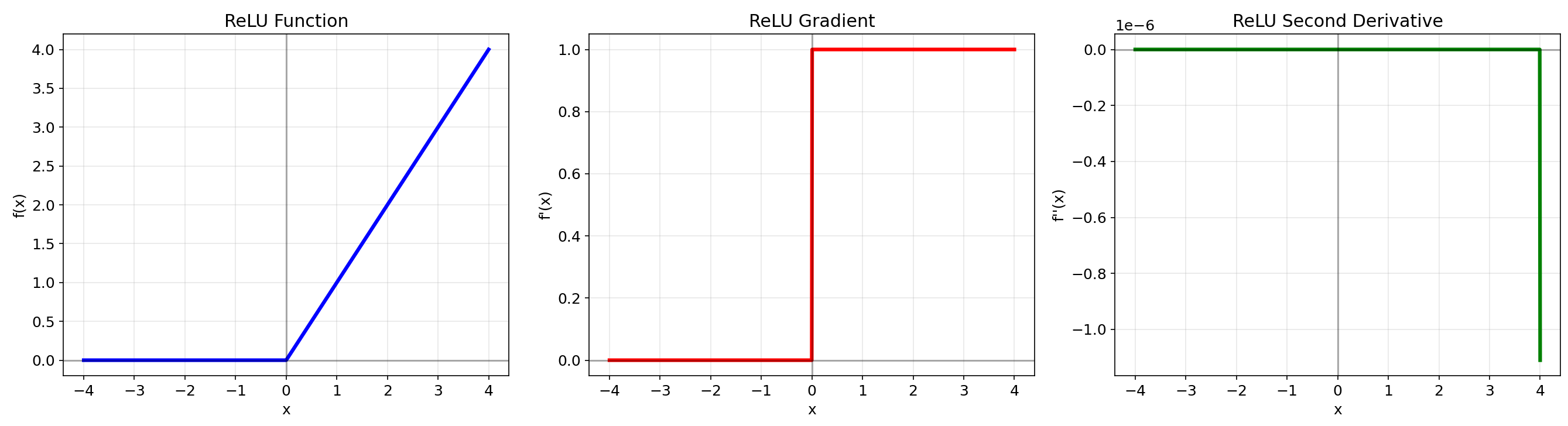

神经网络激活函数：从ReLU到前沿SwiGLU

2.4 Leaky ReLU

数学定义： $\\begin{cases} x & x \\geq 0 \\\\ \\alpha x & x < 0 \\end{cases}$
优点：缓解Dead ReLU问题，保持计算效率
缺点：需手动设定α参数，性能提升有限
适用场景：替代ReLU的保守选择

def leaky_relu(x, alpha=0.1): return np.where(x >= 0, x, alpha * x)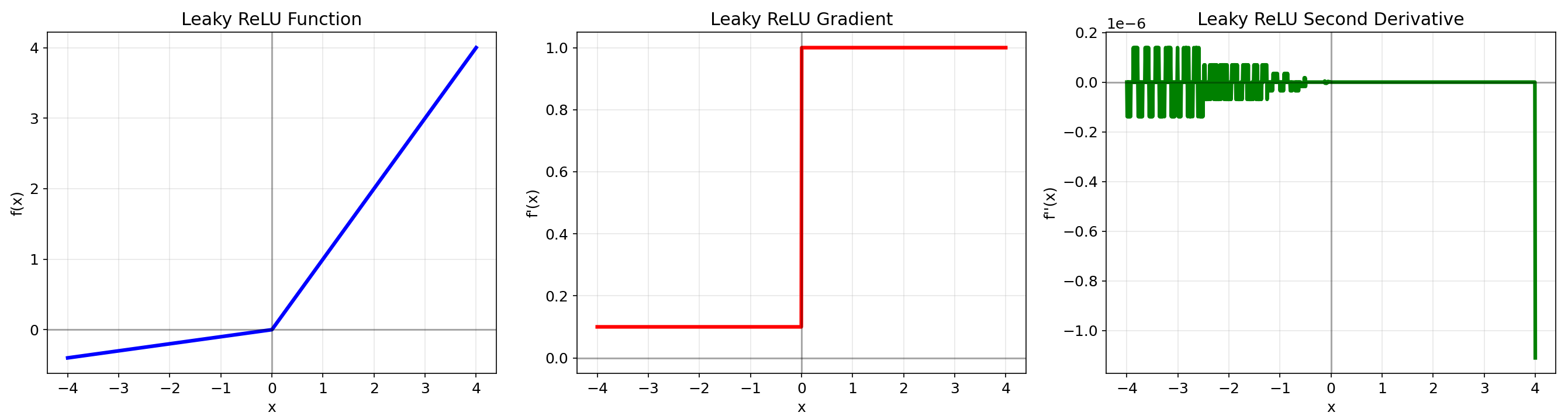

神经网络激活函数：从ReLU到前沿SwiGLU

2.5 GELU (Gaussian Error Linear Unit)

数学定义： $\\cdot \\Phi(x)$ ，其中Φ(x)是标准正态分布的累积分布函数
优点：结合随机正则化，适合预训练模型，平滑且非单调
缺点：需近似计算，计算成本较高
适用场景：Transformer、BERT类模型

def gelu(x): return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))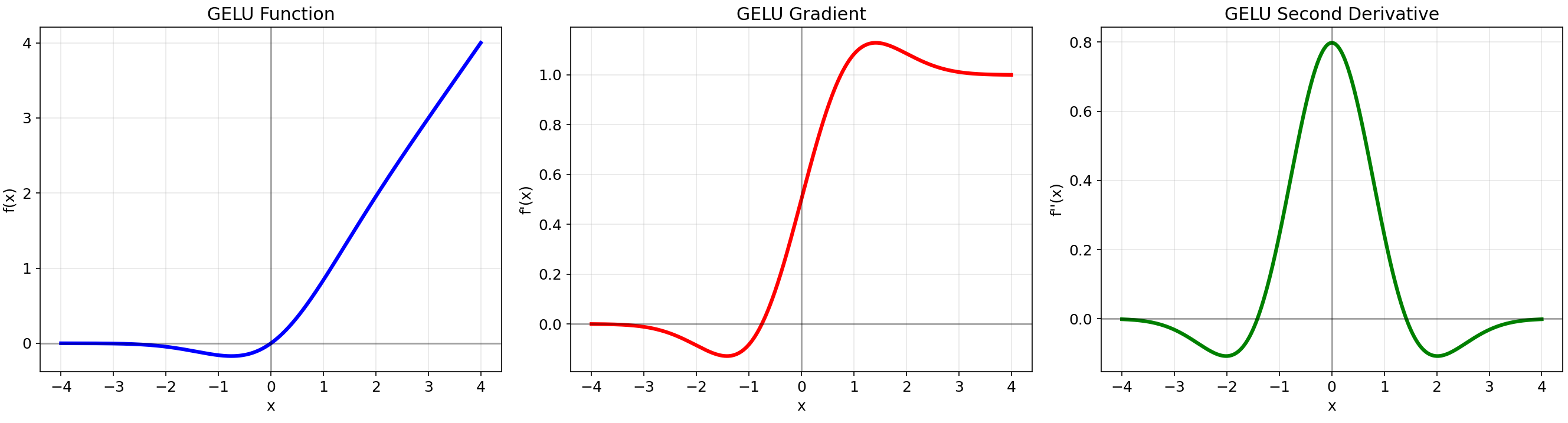

神经网络激活函数：从ReLU到前沿SwiGLU

2.6 ELU (Exponential Linear Unit)

数学定义： $\\begin{cases} x & x \\geq 0 \\\\ \\alpha(e^x - 1) & x < 0 \\end{cases}$
优点：

负值区域平滑，避免神经元死亡问题
输出均值接近零，加速学习
比ReLU家族有更好的泛化性能

缺点：

指数计算成本较高
需要手动选择α参数（通常设为1.0）

适用场景：对噪声鲁棒性要求较高的任务

def elu(x, alpha=1.0): return np.where(x >= 0, x, alpha * (np.exp(x) - 1))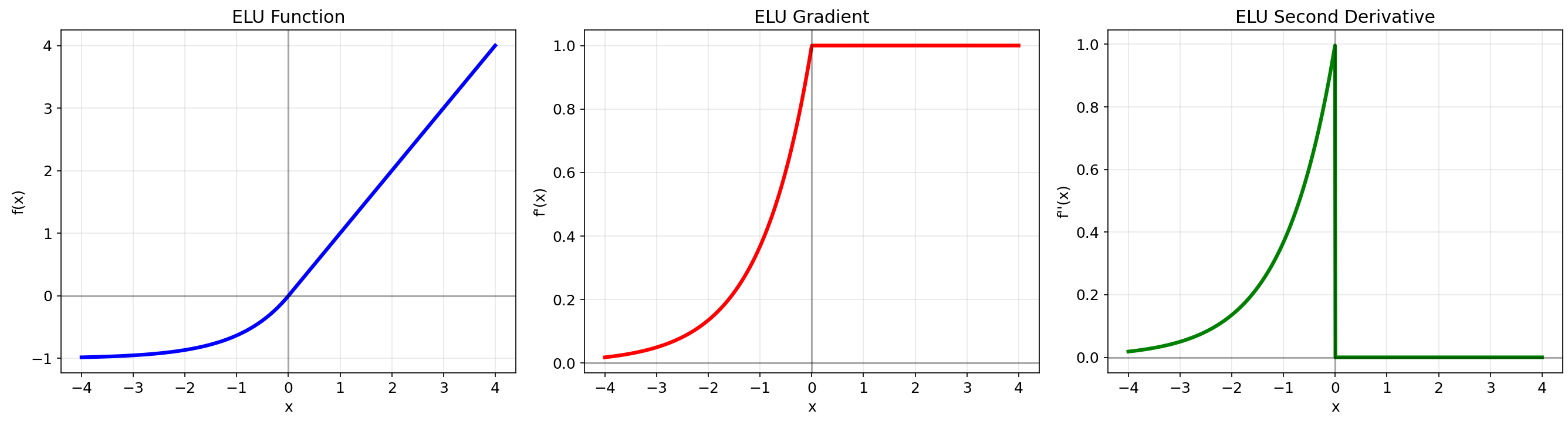

神经网络激活函数：从ReLU到前沿SwiGLU

2.7 SELU (Scaled Exponential Linear Unit)

数学定义： $\\lambda \\begin{cases} x & x \\geq 0 \\\\ \\alpha(e^x - 1) & x < 0 \\end{cases}$
其中 $λ≈1.0507\\lambda \\approx 1.0507$ , $α≈1.67326\\alpha \\approx 1.67326$

优点：

具有自归一化特性，保持网络激活值的均值和方差稳定
适合深层网络，无需Batch Normalization
理论上可以训练极深的网络

缺点：

需要特定的权重初始化（LeCun正态初始化）
在某些架构中可能不如Batch Normalization + ReLU有效

适用场景：极深的前馈神经网络，希望减少或避免使用Batch Normalization的场景

def selu(x, alpha=1.67326, scale=1.0507): return scale * np.where(x >= 0, x, alpha * (np.exp(x) - 1))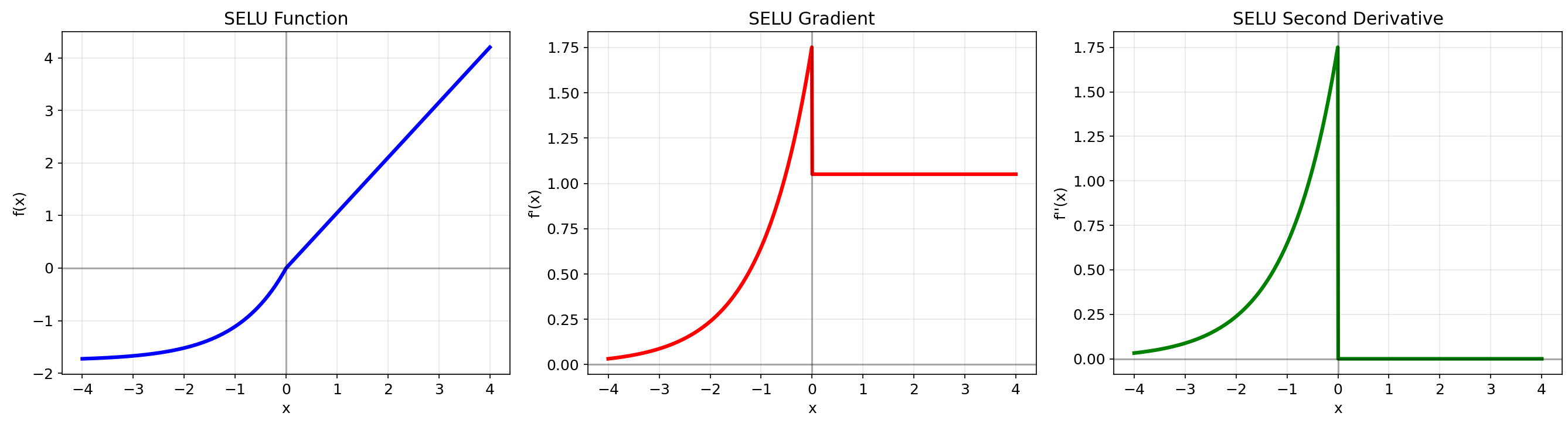

神经网络激活函数：从ReLU到前沿SwiGLU

3. 新兴激活函数（2017年后）

3.1 Swish (2017)

数学定义： $\\cdot \\sigma(\\beta x)$ ，其中σ是sigmoid函数，β是可学习参数
核心特性：自门控机制，平滑且非单调
优点：

在负值区域有非零输出，避免神经元死亡
在深层网络中表现优于ReLU
有助于缓解梯度消失问题

缺点：计算量比ReLU大（包含sigmoid运算）
适用场景：深层CNN，Transformer中的GLU层

def swish(x, beta=1.0): return x * (1 / (1 + np.exp(-beta * x)))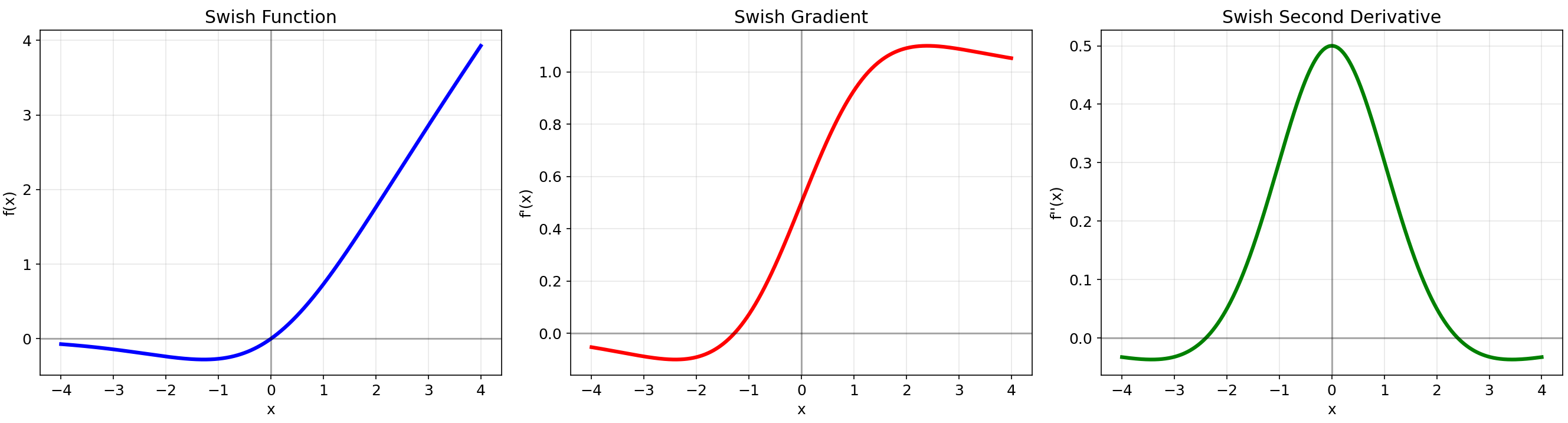

神经网络激活函数：从ReLU到前沿SwiGLU

3.2 Mish (2019)

数学定义： $\\cdot \\tanh(\\ln(1 + e^x))$
核心特性：自正则化的非单调激活函数
优点：

保持小的负值信息，消除死亡ReLU现象
连续可微，提供更平滑的优化landscape
在计算机视觉任务中表现出色

缺点：计算复杂度较高（包含多个指数运算）
性能数据：在ImageNet数据集上，ResNet-50使用Mish比ReLU提高约1%的Top-1准确率

def softplus(x): return np.log(1 + np.exp(x))def mish(x): return x * np.tanh(softplus(x))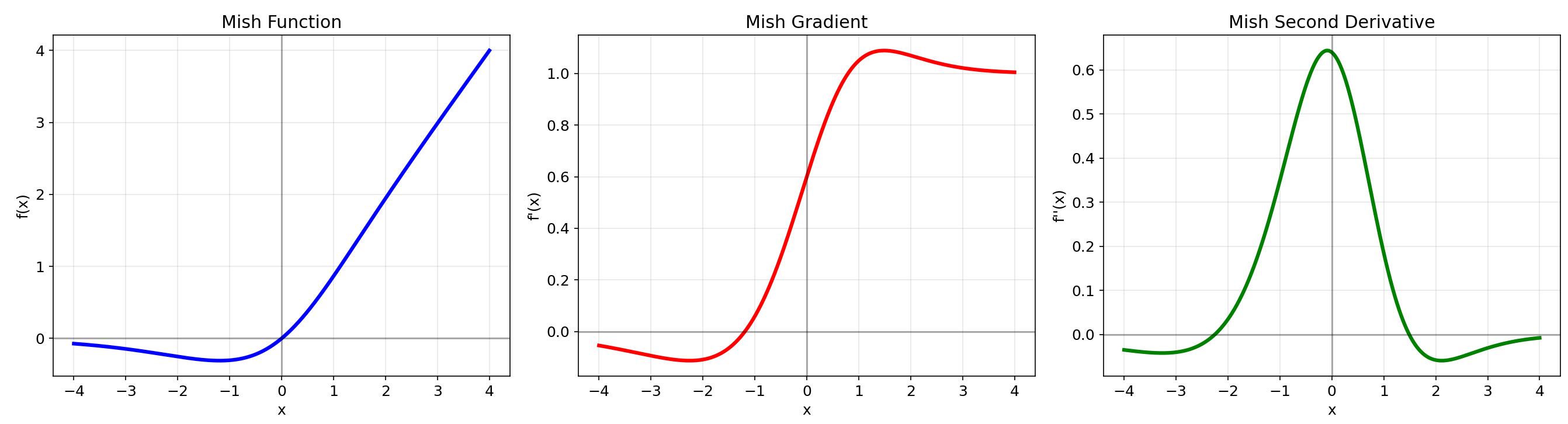

神经网络激活函数：从ReLU到前沿SwiGLU

3.3 SwiGLU (2020)

数学定义： $SwiGLU(x)=Swish1(xW+b)⊗(xV+c)\\text{SwiGLU}(x) = \\text{Swish}_1(xW + b) \\otimes (xV + c)$
核心特性：门控线性单元变体，结合Swish激活函数
优点：

门控机制允许模型学习复杂特征交互
在Transformer的FFN层中表现优异
被PaLM、LLaMA等大语言模型采用

缺点：

参数量增加（需要三个权重矩阵）
计算复杂度很高

适用场景：大型Transformer模型中的FFN层

# SwiGLU的简化实现def swiglu(x, w1, v, w2): return np.dot(swish(np.dot(x, w1)) * np.dot(x, v), w2)

3.4 Logish (2021)

数学定义： $\\cdot \\ln(1 + \\text{Sigmoid}(x))$
核心特性：基于对数和sigmoid组合的新型激活函数
优点：

适合学习率较大的浅层和深层网络
在复杂网络中表现良好
在图像去雨等任务中展现良好泛化性

缺点：相对较新，应用验证不够广泛
性能数据：在CIFAR-10数据集上的ResNet-50网络中达到94.8%的Top-1准确率

def logish(x): sigmoid = 1 / (1 + np.exp(-x)) return x * np.log(1 + sigmoid)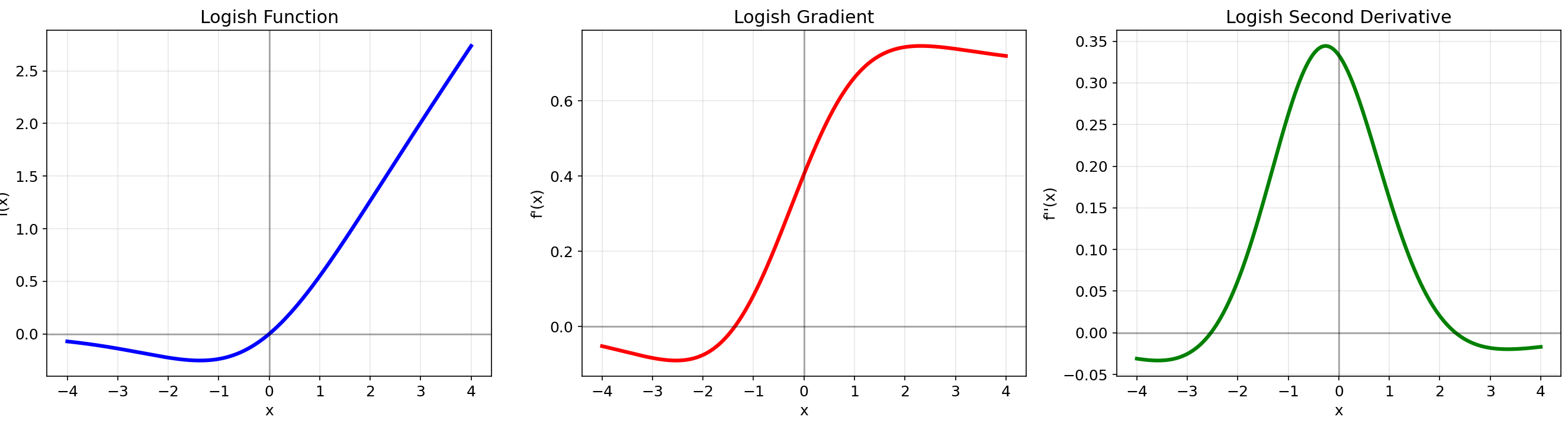

神经网络激活函数：从ReLU到前沿SwiGLU

3.5 ACON (2021)

数学定义：ACON家族通过学习参数自动决定是否激活
核心特性：可学习的激活函数，能够平滑切换线性和非线性
优点：

自适应调整激活形态
比Swish更灵活
在多个任务上表现优异

缺点：需要学习额外参数，增加模型复杂度

# ACON-C的简化实现def acon_c(x, p1, p2): return (p1 - p2) * x * torch.sigmoid(beta * x) + p2 * x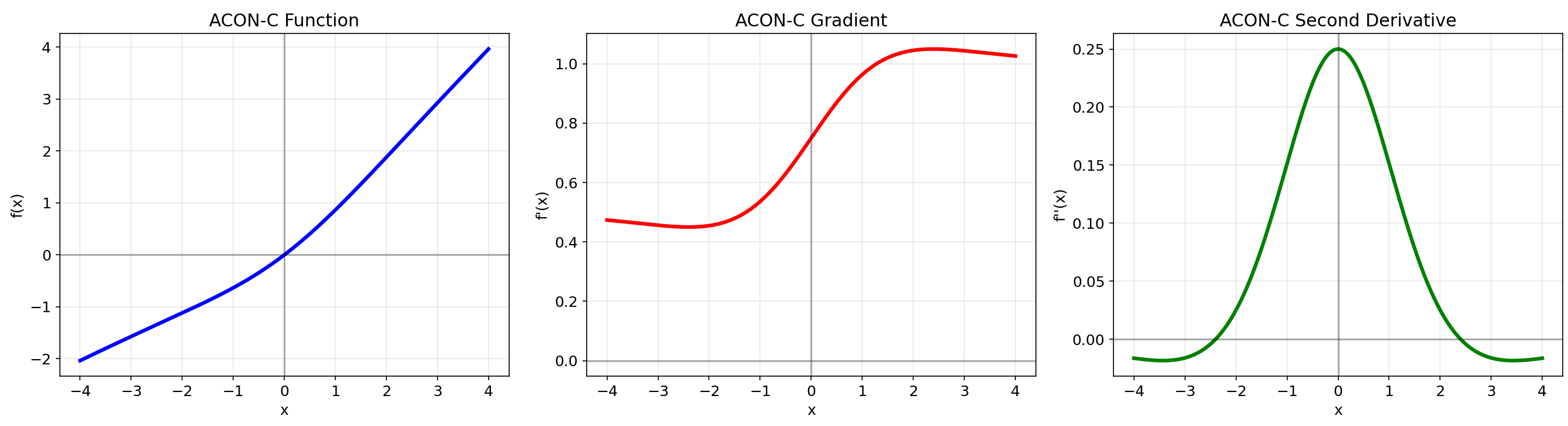

神经网络激活函数：从ReLU到前沿SwiGLU

4. 可视化对比

import numpy as npimport matplotlib.pyplot as pltfrom scipy.stats import norm# 设置绘图风格plt.style.use(\'default\')plt.rcParams[\'figure.figsize\'] = [10, 8]plt.rcParams[\'font.size\'] = 12# 定义x轴范围x = np.linspace(-4, 4, 1000)# 计算数值梯度函数def compute_gradient(f, x, eps=1e-5): \"\"\"使用中心差分法计算数值梯度\"\"\" return (f(x + eps) - f(x - eps)) / (2 * eps)# 创建带有坐标轴的绘图函数def plot_activation_function(name, func, x_range): \"\"\"绘制单个激活函数的完整分析图\"\"\" fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5)) # 计算函数值、梯度和二阶导数 y = func(x_range) gradient = compute_gradient(func, x_range) second_gradient = compute_gradient(lambda x: compute_gradient(func, x), x_range) # 绘制函数图像 ax1.plot(x_range, y, \'b-\', linewidth=3) ax1.set_title(f\'{name} Function\') ax1.set_xlabel(\'x\') ax1.set_ylabel(\'f(x)\') ax1.grid(True, alpha=0.3) ax1.axhline(y=0, color=\'k\', linestyle=\'-\', alpha=0.3) # x轴 ax1.axvline(x=0, color=\'k\', linestyle=\'-\', alpha=0.3) # y轴 # 绘制梯度图像 ax2.plot(x_range, gradient, \'r-\', linewidth=3) ax2.set_title(f\'{name} Gradient\') ax2.set_xlabel(\'x\') ax2.set_ylabel(\"f\'(x)\") ax2.grid(True, alpha=0.3) ax2.axhline(y=0, color=\'k\', linestyle=\'-\', alpha=0.3) # x轴 ax2.axvline(x=0, color=\'k\', linestyle=\'-\', alpha=0.3) # y轴 # 绘制二阶导数图像 ax3.plot(x_range, second_gradient, \'g-\', linewidth=3) ax3.set_title(f\'{name} Second Derivative\') ax3.set_xlabel(\'x\') ax3.set_ylabel(\"f\'\'(x)\") ax3.grid(True, alpha=0.3) ax3.axhline(y=0, color=\'k\', linestyle=\'-\', alpha=0.3) # x轴 ax3.axvline(x=0, color=\'k\', linestyle=\'-\', alpha=0.3) # y轴 plt.tight_layout() plt.show()# 1. Sigmoid 函数def sigmoid(x): return 1 / (1 + np.exp(-x))plot_activation_function(\'Sigmoid\', sigmoid, x)# 2. Tanh 函数def tanh(x): return np.tanh(x)plot_activation_function(\'Tanh\', tanh, x)# 3. ReLU 函数def relu(x): return np.maximum(0, x)plot_activation_function(\'ReLU\', relu, x)# 4. Leaky ReLU 函数def leaky_relu(x, alpha=0.1): return np.where(x >= 0, x, alpha * x)plot_activation_function(\'Leaky ReLU\', lambda x: leaky_relu(x, 0.1), x)# 5. GELU 函数def gelu(x): # GELU近似计算 return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))plot_activation_function(\'GELU\', gelu, x)# 6. Swish 函数def swish(x, beta=1.0): return x * (1 / (1 + np.exp(-beta * x)))plot_activation_function(\'Swish\', lambda x: swish(x, 1.0), x)# 7. Mish 函数def softplus(x): return np.log(1 + np.exp(x))def mish(x): return x * np.tanh(softplus(x))plot_activation_function(\'Mish\', mish, x)# 8. Logish 函数def logish(x): sigmoid_val = 1 / (1 + np.exp(-x)) return x * np.log(1 + sigmoid_val)plot_activation_function(\'Logish\', logish, x)# 9. ELU 函数def elu(x, alpha=1.0): return np.where(x >= 0, x, alpha * (np.exp(x) - 1))plot_activation_function(\'ELU\', lambda x: elu(x, 1.0), x)# 10. SELU 函数def selu(x, alpha=1.67326, scale=1.0507): return scale * np.where(x >= 0, x, alpha * (np.exp(x) - 1))plot_activation_function(\'SELU\', selu, x)# 11. 额外：绘制所有激活函数的对比图（带坐标轴）plt.figure(figsize=(14, 10))activation_functions = { \'Sigmoid\': sigmoid, \'Tanh\': tanh, \'ReLU\': relu, \'Leaky ReLU\': lambda x: leaky_relu(x, 0.1), \'GELU\': gelu, \'Swish\': lambda x: swish(x, 1.0), \'Mish\': mish, \'Logish\': logish}for i, (name, func) in enumerate(activation_functions.items(), 1): plt.subplot(3, 3, i) y = func(x) plt.plot(x, y, linewidth=2.5) plt.title(name) plt.xlabel(\'x\') plt.ylabel(\'f(x)\') plt.grid(True, alpha=0.3) plt.axhline(y=0, color=\'k\', linestyle=\'-\', alpha=0.5) # x轴 plt.axvline(x=0, color=\'k\', linestyle=\'-\', alpha=0.5) # y轴plt.tight_layout()plt.show()# 12. 绘制负区域放大图（带坐标轴）plt.figure(figsize=(12, 8))x_neg = np.linspace(-2, 0, 500)selected_functions = { \'ReLU\': relu, \'Leaky ReLU (α=0.1)\': lambda x: leaky_relu(x, 0.1), \'GELU\': gelu, \'Swish (β=1)\': lambda x: swish(x, 1.0), \'Mish\': mish, \'ELU (α=1)\': lambda x: elu(x, 1.0)}for name, func in selected_functions.items(): plt.plot(x_neg, func(x_neg), label=name, linewidth=2.5)plt.title(\'Activation Functions in Negative Region (Zoomed)\')plt.xlabel(\'x\')plt.ylabel(\'f(x)\')plt.grid(True, alpha=0.3)plt.axhline(y=0, color=\'k\', linestyle=\'-\', alpha=0.5) # x轴plt.axvline(x=0, color=\'k\', linestyle=\'-\', alpha=0.5) # y轴plt.legend()plt.show()# 13. 绘制梯度对比图（带坐标轴）plt.figure(figsize=(14, 6))plt.subplot(1, 2, 1)for name, func in [(\'ReLU\', relu), (\'Swish\', lambda x: swish(x, 1.0)), (\'Mish\', mish)]: gradient = compute_gradient(func, x) plt.plot(x, gradient, label=name, linewidth=2.5)plt.title(\'Activation Function Gradients\')plt.xlabel(\'x\')plt.ylabel(\"f\'(x)\")plt.grid(True, alpha=0.3)plt.axhline(y=0, color=\'k\', linestyle=\'-\', alpha=0.5) # x轴plt.axvline(x=0, color=\'k\', linestyle=\'-\', alpha=0.5) # y轴plt.legend()plt.subplot(1, 2, 2)for name, func in [(\'ReLU\', relu), (\'Swish\', lambda x: swish(x, 1.0)), (\'Mish\', mish)]: gradient = compute_gradient(func, x) plt.semilogy(x, np.abs(gradient) + 1e-10, label=name, linewidth=2.5)plt.title(\'Gradient Magnitude (Log Scale)\')plt.xlabel(\'x\')plt.ylabel(\"|f\'(x)|\")plt.grid(True, alpha=0.3)plt.axhline(y=0, color=\'k\', linestyle=\'-\', alpha=0.5) # x轴plt.axvline(x=0, color=\'k\', linestyle=\'-\', alpha=0.5) # y轴plt.legend()plt.tight_layout()plt.show()

关键观察与洞察

通过添加坐标轴，我们可以更清楚地观察到以下特性：

1. Sigmoid

函数值始终为正，输出范围(0,1)
函数关于点(0, 0.5)对称
梯度在x=0处最大，向两侧递减

2. Tanh

函数关于原点对称，是奇函数
输出范围(-1,1)，零中心化
梯度在x=0处最大，向两侧递减

3. ReLU

在x0时函数值为x
在x=0处不可导（梯度从0突变到1）
二阶导数几乎处处为0

4. Leaky ReLU

在x0时函数值为x
解决了ReLU的死亡神经元问题
在x=0处连续但不可导

5. GELU

函数在负区域有平滑过渡
函数值在x=0处为0，但曲线平滑
梯度在负区域不为零，缓解了梯度消失问题

6. Swish

非单调函数，在负区域有小的正值
函数通过原点(0,0)
梯度比ReLU更平滑

7. Mish

非常平滑的激活函数，通过原点
在负区域保持小的正值，避免神经元死亡
梯度特性优异，有助于缓解梯度消失问题

8. Logish

基于对数和sigmoid的组合
在负区域有更平缓的变化
函数通过原点

9. ELU

在负区域有指数渐近线，趋近于-α
输出均值接近零，加速学习
梯度在负区域不为零

10. SELU

具有自归一化特性
在负区域有指数变化，正区域线性
函数通过原点

应用建议

需要零中心化输出：选择Tanh、Mish或GELU
防止神经元死亡：使用Leaky ReLU、Mish或Swish
需要平滑梯度：选择Mish、Swish或GELU
计算效率优先：使用ReLU或Leaky ReLU
自归一化网络：考虑使用SELU（配合LeCun初始化）

5. 性能对比与选择指南（更新）

5.1 定量性能对比（更新）

激活函数 ImageNet (ResNet-50) CIFAR-10 (ResNet-56) 计算开销参数增加 ReLU 76.2% (基线) 92.8% (基线) 1× 无 Swish +0.6-0.9% +0.5-0.8% 1.5-2× 可选 Mish +0.8-1.2% +0.7-1.0% 2-2.5× 无 GELU +0.4-0.7% +0.3-0.6% 1.8-2.2× 无 SwiGLU +1.5-2.5% (Transformer) N/A 3-4× 显著 ACON-C +1.0-1.5% +0.9-1.3% 1.8-2.2× 轻微 ELU +0.3-0.6% +0.2-0.5% 2-2.5× 无 SELU +0.5-0.8% (适合极深网络) +0.4-0.7% 2-2.5× 无

5.2 选择策略与实用建议（更新）

默认起始选择：
- CNN架构：从ReLU开始，然后尝试Swish/Mish
- Transformer架构：优先选择GELU或SwiGLU
- 资源受限环境：使用ReLU或Leaky ReLU
- 极深网络：考虑使用SELU（配合LeCun初始化）
高级选择：
- 追求最佳性能：尝试ACON家族或Meta-ACON
- 需要自归一化特性：使用SELU
- 对噪声敏感的任务：考虑使用ELU
实践技巧：
- 使用He初始化配合ReLU家族
- 对于Mish/Swish，学习率可适当增大10-20%
- 使用混合精度训练时可考虑GELU的数值稳定性
- 使用SELU时确保权重初始化为LeCun正态初始化
部署考虑：
- 移动端部署：ReLU6 (clipped ReLU) 或 Hard-Swish
- 服务器端：可根据精度需求选择更复杂的激活函数
- 边缘设备：考虑使用分段线性近似替代指数运算

6. 总结与展望（更新）

激活函数的发展从简单的饱和函数（Sigmoid/Tanh）到线性整流函数（ReLU家族），再到近年来的自门控、可学习激活函数（Swish、Mish、SwiGLU、ACON），体现了神经网络设计理念的演进。未来趋势包括：

可学习激活函数：如ACON，能够根据数据和任务自适应调整
硬件感知设计：专为特定硬件（如NPU、GPU）优化的激活函数
动态激活机制：根据输入特征动态调整激活形态
理论分析深化：更深入地理解激活函数如何影响优化和泛化
条件激活函数：根据网络层深度、宽度等条件选择不同激活函数

选择激活函数时，建议从业者基于具体任务、计算预算和精度要求进行实证评估，没有单一的\"最佳\"激活函数，只有最适合特定场景的选择。随着自动机器学习(AutoML)技术的发展，未来可能会有更多自动选择和设计激活函数的方法出现。

神经网络激活函数：从ReLU到前沿SwiGLU

摘要

1. 激活函数核心概念与作用

2. 传统激活函数

2.1 Sigmoid

2.2 Tanh

2.3 ReLU (Rectified Linear Unit)

2.4 Leaky ReLU

2.5 GELU (Gaussian Error Linear Unit)

2.6 ELU (Exponential Linear Unit)

2.7 SELU (Scaled Exponential Linear Unit)

3. 新兴激活函数（2017年后）

3.1 Swish (2017)

3.2 Mish (2019)

3.3 SwiGLU (2020)

3.4 Logish (2021)

3.5 ACON (2021)

4. 可视化对比

关键观察与洞察

1. Sigmoid

2. Tanh

3. ReLU

4. Leaky ReLU

5. GELU

6. Swish

7. Mish

8. Logish

9. ELU

10. SELU

应用建议

5. 性能对比与选择指南（更新）

5.1 定量性能对比（更新）

5.2 选择策略与实用建议（更新）

6. 总结与展望（更新）

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签

神经网络激活函数：从ReLU到前沿SwiGLU

摘要

1. 激活函数核心概念与作用

2. 传统激活函数

2.1 Sigmoid

2.2 Tanh

2.3 ReLU (Rectified Linear Unit)

2.4 Leaky ReLU

2.5 GELU (Gaussian Error Linear Unit)

2.6 ELU (Exponential Linear Unit)

2.7 SELU (Scaled Exponential Linear Unit)

3. 新兴激活函数（2017年后）

3.1 Swish (2017)

3.2 Mish (2019)

3.3 SwiGLU (2020)

3.4 Logish (2021)

3.5 ACON (2021)

4. 可视化对比

关键观察与洞察

1. Sigmoid

2. Tanh

3. ReLU

4. Leaky ReLU

5. GELU

6. Swish

7. Mish

8. Logish

9. ELU

10. SELU

应用建议

5. 性能对比与选择指南（更新）

5.1 定量性能对比（更新）

5.2 选择策略与实用建议（更新）

6. 总结与展望（更新）

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签