【C++】哈希表:从概念到代码实现_哈希biaoc++
🌟 快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。🌟

在计算机科学的奇妙世界里,哈希表(Hash Table)如同一个神奇的百宝箱,能快速地对数据进行存储和查找。接下来,让我们一起深入探索哈希表的奥秘吧🧐。
目录
一、哈希概念大揭秘🤓
直接定址法:简单直接的 “数据定位器”📌
哈希冲突:前进路上的 “小阻碍”🚧
将关键字转为整数:数据处理的 “小窍门”🔢
哈希函数:神奇的 “数据映射魔法师”✨
二、处理哈希冲突的妙招🌟
开放定址法:在哈希表内 “寻找空位”🪑
开放定址法代码实现:用代码构建 “数据家园”💻
链地址法代码实现:打造高效的 “数据链表网” 💡
三、总结:哈希表的奇妙世界🎊
一、哈希概念大揭秘🤓
哈希(hash)又称散列,从名字上看就有一种 “把数据打散、排列” 的感觉😜。它的核心原理是借助哈希函数,在关键字(Key)和存储位置之间建立起一种特殊的映射关系。如此一来,查找数据时,通过这个哈希函数算出关键字的存储位置,就能像施了魔法一样迅速找到目标数据✨。
直接定址法:简单直接的 “数据定位器”📌
当关键字的范围比较集中时,直接定址法就像一把精准的钥匙,简单又高效。例如,若一组关键字都在这个区间内,我们只需创建一个长度为 100 的数组,关键字的值直接就对应数组存储位置的下标。再比如,关键字是小写字母时,创建一个大小为 26 的数组,通过关键字的 ASCII 码减去 \'a\' 的 ASCII 码,得到的结果就是存储位置的下标。在计数排序和一些 OJ 题目中,都能看到它大展身手的身影呢👏。以 LeetCode 的 387. 字符串中的第一个唯一字符这道题为例,代码利用这种方法,将每个字母的 ASCII 码 - \'a\' 的 ASCII 码作为下标映射到 count 数组,以此统计字符出现的次数,从而轻松找出第一个唯一字符,是不是很厉害呀😎?
class Solution {public: int firstUniqChar(string s) { int count[26] = {0}; for (auto ch : s) { count[ch - \'a\']++; } for (size_t i = 0; i < s.size(); ++i) { if (count[s[i] - \'a\'] == 1) { return i; } } return -1; }};代码利用直接定址法,将每个字母的 ASCII 码 - \'a\' 的 ASCII 码作为下标映射到 count 数组,统计字符出现的次数,进而快速找出第一个唯一字符
哈希冲突:前进路上的 “小阻碍”🚧
直接定址法虽好,但存在局限性。当关键字范围分散时,会面临内存浪费甚至内存不足的问题。此时需借助哈希函数(hash function)将关键字 key 映射到数组的 h (key) 位置(h (key) 的值需在 [0, M) 之间,M 为数组空间大小)。然而,不同的 key 可能会映射到同一位置,这就是哈希冲突(Hash Conflict),也叫哈希碰撞(Hash Collision)。尽管我们期望找到完美的哈希函数来避免冲突,但实际中冲突难以避免😫。因此,不仅要设计优秀的哈希函数减少冲突次数,还要制定有效的冲突解决策略。
负载因子:衡量哈希表性能的 “标尺”⚖️
负载因子(Load Factor)是哈希表中的重要指标,它如同一个精准的 “标尺”,衡量着哈希表的性能。负载因子越大,哈希冲突的概率越高,但空间利用率也越高;反之,负载因子越小,哈希冲突概率越低,空间利用率也越低。假设哈希表已存储 N 个值,哈希表大小为 M,负载因子的计算公式为:负载因子 = N / M 。在实际应用中,需要合理控制负载因子,以达到哈希表性能的最佳平衡。
将关键字转为整数:数据处理的 “小窍门”🔢
通常,将关键字映射到数组位置时,整数更便于进行映射计算。若关键字不是整数,就需要想办法将其转换为整数。这个转换过程在后续代码实现中会有详细展示。在讨论哈希函数时,如果关键字不是整数,那么此处讨论的 Key 实际上是转换后的整数。
哈希函数:神奇的 “数据映射魔法师”✨
一个理想的哈希函数,就像一位神奇的 “魔法师”,能让 N 个关键字均匀地分布在哈希表的 M 个空间中。虽然实际中很难做到完美,但我们要朝着这个目标努力设计。常见的哈希函数有以下几种:
- 除法散列法 / 除留余数法:除法散列法,也叫除留余数法,原理是用 key 除以 M 的余数作为映射位置的下标,即哈希函数为
。但要注意,应尽量避免 M 取 2 的幂、10 的幂等特殊值,否则可能导致冲突。例如,当 M 是 16(即 )时,63 和 31 计算出的哈希值都是 15 。所以,一般建议 M 取不太接近 2 的整数次幂的质数。不过在实践中,像 Java 的 HashMap 采用除法散列法时,会用 2 的整数次幂做哈希表的大小 M ,通过位运算提高效率,同时让 key 的所有位都参与计算,使映射出的哈希值更均匀。
二、处理哈希冲突的妙招🌟
实践中,哈希表常采用除法散列法作为哈希函数,但无论选择哪种哈希函数,冲突都难以避免。那么在插入数据时,该如何解决冲突呢?主要有开放定址法和链地址法这两种方法。
开放定址法:在哈希表内 “寻找空位”🪑
在开放定址法中,所有元素都存储在哈希表内。当一个关键字 key 用哈希函数计算出的位置发生冲突时,会按照某种规则寻找一个没有存储数据的位置进行存储。开放定址法的负载因子一定小于 1,其规则有线性探测、二次探测、双重探测三种。
- 线性探测:从发生冲突的位置开始,依次线性向后探测,若走到哈希表尾,则回绕到哈希表头的位置,直到找到下一个没有存储数据的位置。线性探测简单易实现,但可能出现群集(堆积)现象。
- 二次探测:从发生冲突的位置开始,依次左右按二次方跳跃式探测,若走到哈希表尾或表头,则回绕到相应位置,直到找到空位。二次探测能在一定程度上改善群集问题。
下面演示 {19,30,5,36,13,20,21,12} 等这⼀组值映射到M=11的表中。

h(19) = 8,h(30) = 8,h(5) = 5,h(36) = 3,h(13) = 2,h(20) = 9,h(21) =10,h(12) = 1

开放定址法代码实现:用代码构建 “数据家园”💻
开放定址法在实践中不如链地址法常用,这里我们简单选择线性探测来实现。在代码实现中,需要给每个存储值的位置添加一个状态标识,否则删除值后可能影响后续冲突值的查找。同时,我们将哈希表负载因子控制在 0.7,达到该值时进行扩容。当 key 是 string/Date 等类型不能直接取模时,需要给 HashTable 增加一个仿函数,将 key 转换为可以取模的整形。下面是开放定址法的完整代码实现:
enum Status{EMPTY,EXIST,DELETE};templatestruct HashData{pair _kv;Status _s; //状态};//HashFunctemplatestruct HashFunc{size_t operator()(const K& key){return (size_t)key;}};//HashFunctemplatestruct HashFunc{size_t operator()(const string& key){// BKDRsize_t hash = 0;for (auto e : key){hash *= 31;hash += e;}cout << key << \":\" << hash << endl;return hash;}};template<class K, class V, class Hash = HashFunc>class HashTable{public:HashTable(){_tables.resize(10);}bool Insert(const pair& kv){if (Find(kv.first))return false;// 负载因子0.7就扩容if (_n*10 / _tables.size() == 7){size_t newSize = _tables.size() * 2;HashTable newHT;newHT._tables.resize(newSize);// 遍历旧表for (size_t i = 0; i < _tables.size(); i++){if (_tables[i]._s == EXIST){newHT.Insert(_tables[i]._kv);}}_tables.swap(newHT._tables);}Hash hf;// 线性探测size_t hashi = hf(kv.first) % _tables.size();while (_tables[hashi]._s == EXIST){hashi++;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._s = EXIST;++_n;return true;}HashData* Find(const K& key){Hash hf;size_t hashi = hf(key) % _tables.size();while (_tables[hashi]._s != EMPTY){if (_tables[hashi]._s == EXIST&& _tables[hashi]._kv.first == key){return &_tables[hashi];}hashi++;hashi %= _tables.size();}return NULL;}// 伪删除法bool Erase(const K& key){HashData* ret = Find(key);if (ret){ret->_s = DELETE;--_n;return true;}else{return false;}}void Print(){for (size_t i = 0; i %d\\n\", i, _tables[i]._kv.first);cout << \"[\" << i <\" << _tables[i]._kv.first <<\":\" << _tables[i]._kv.second<\\n\", i);}else{printf(\"[%d]->D\\n\", i);}}cout << endl;}private:vector<HashData> _tables;size_t _n = 0; // 存储的关键字的个数};
链地址法代码实现:打造高效的 “数据链表网” 💡
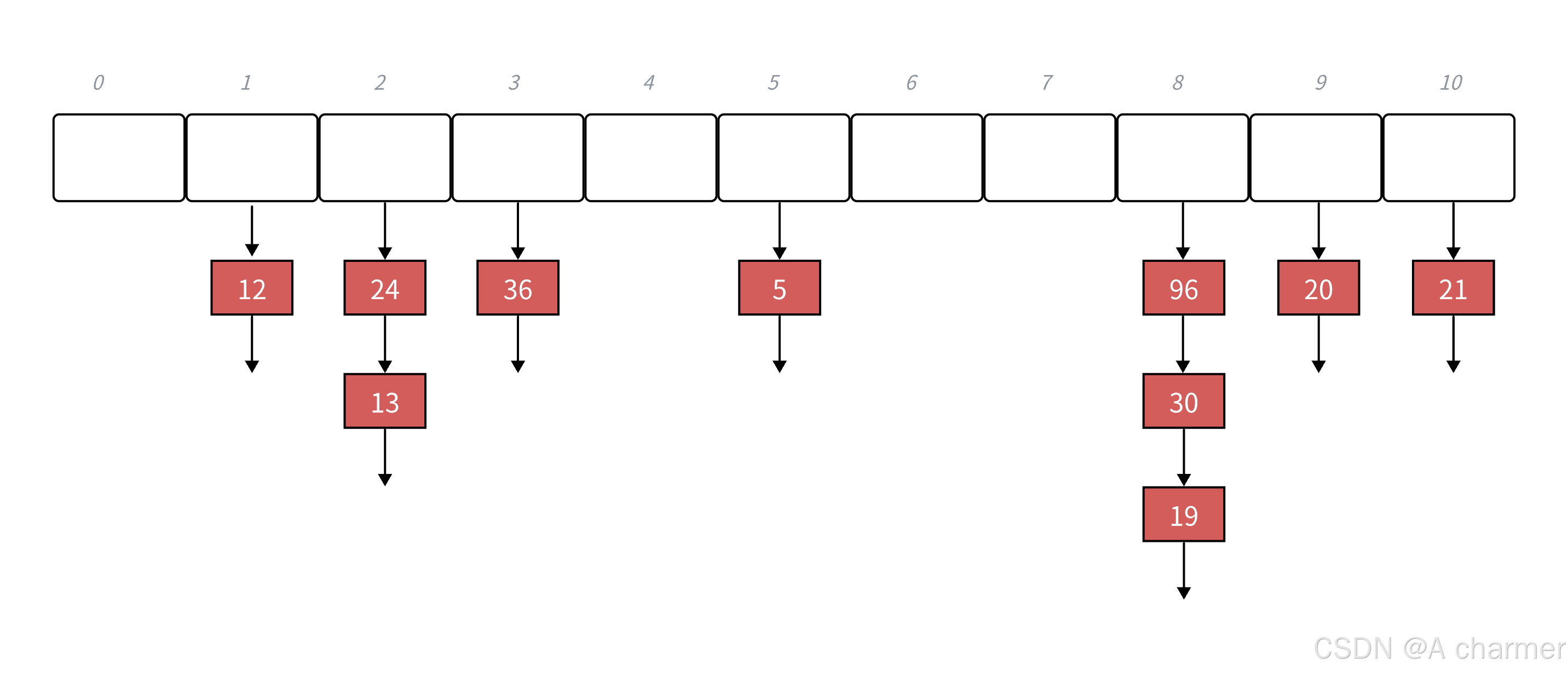
下面演示 {19,30,5,36,13,20,21,12,24,96} 等这⼀组值映射到M=11的表中。

h(19) = 8,h(30) = 8,h(5) = 5,h(36) = 3,h(13) = 2,h(20) = 9,h(21) =10,h(12) = 1,h(24) = 2,h(96) = 88
链地址法的负载因子没有限制,stl 中 unordered_xxx 的最大负载因子基本控制在 1,大于 1 就扩容。下面是链地址法的代码实现:
namespace hash_bucket { template struct HashNode { HashNode* _next; std::pair _kv; HashNode(const std::pair& kv) :_kv(kv) , _next(nullptr) {} }; template class HashTable { typedef HashNode Node; public: HashTable() { _tables.resize(10); } ~HashTable() { for (size_t i = 0; i _next; delete cur; cur = next; } _tables[i] = nullptr; } } bool Insert(const std::pair& kv) { if (Find(kv.first)) return false; if (_n == _tables.size()) { size_t newSize = _tables.size() * 2; HashTable newHT; newHT._tables.resize(newSize); for (size_t i = 0; i _kv); cur = cur->_next; } } _tables.swap(newHT._tables); } size_t hashi = kv.first % _tables.size(); Node* newnode = new Node(kv); newnode->_next = _tables[hashi]; _tables[hashi] = newnode; ++_n; return true; } Node* Find(const K& key) { size_t hashi = key % _tables.size(); Node* cur = _tables[hashi]; while (cur) { if (cur->_kv.first == key) { return cur; } cur = cur->_next; } return nullptr; } private: std::vector _tables; size_t _n = 0; };}三、总结:哈希表的奇妙世界🎊
哈希表作为一种强大的数据结构,在计算机科学中有着广泛的应用。它的性能取决于哈希函数的设计以及冲突处理方法的选择。开放定址法简单直接,但存在元素相互影响的问题;链地址法更加灵活,适用于负载因子较大的场景。在实际应用中,我们需要根据具体需求和数据特点,选择合适的哈希表实现方式,充分发挥其高效查找的优势,为程序性能的提升添砖加瓦💪!
希望通过本文,你对哈希表有了更深入的理解,能够在编程的世界里更好地运用它。
欢迎关注我 👉【A charmer】



