《BrepGen: A B-rep Generative Diffusion Model with Structured Latent Geometry》论文阅读笔记_brep生成模型

这篇论文介绍了一种名为 BrepGen 的创新性生成模型，它能够直接生成工业设计中最为核心和普遍的 边界表示（Boundary representation, B-rep） 格式的CAD模型。该工作的核心在于提出了一种新颖的结构化潜在几何（Structured Latent Geometry） 表示方法，巧妙地将复杂的 B-rep 数据统一到一个神经网络易于处理的层级树结构中，并利用扩散模型（Diffusion Model）进行生成。

背景和动机

• 设计师真实需求——工业级 CAD 往往要对自由曲面和曲面间严丝合缝的拓扑进行后期修改；CSG 或 Sketch-and-Extrude 都会在复杂造型上遇到瓶颈。
• 现有直接 B-rep 方法（SolidGen 等）只能画直棱柱——原因在于它们把“拓扑指针”作为离散分类来预测，组合空间爆炸，网络不收敛。
• BrepGen 的切入点：把“拓扑指针预测”改成“连续几何特征回归 + 事后合并”，借用扩散模型善于回归连续分布的优势。

方法架构

BrepGen 的整体架构可以概括为“树化表示 × 四级扩散”：它先把任意 B-rep 拆成固定宽度的三层树——面、边、顶点——每个节点特征由全局位置包围盒与经 VAE 压缩的局部形状潜码拼接而成；复杂拓扑则通过在树中复制共享元素隐式编码。生成阶段沿树自顶向下串行执行四个条件扩散子任务：

1. 无条件去噪面的位置 FpF_pFp​；
2. 在 FpF_pFp​ 已确定的条件下去噪面的形状潜码 FzF_zFz​；
3. 以面特征 $F$ 为父 token，通过简单的“token 加法”注入条件，去噪各条边的位置 EₚE_ₚEₚ​；
4. 再以 $F$ 和 EₚE_ₚEₚ​ 为条件，去噪边-顶点联合形状潜码 EzvE_{zv}Ezv​。

四个子网共享一套轻量 Transformer 骨干，时步 $t$ 和类别 $c$ 嵌入到每个 token 内。推理时，在第三阶段开始即用几何阈值做早期剪枝并在最终输出前合并重复节点，从而显式恢复邻接拓扑并生成 watertight 的 B-rep 实体。

结构化潜在几何树（SLG）—统一几何与拓扑

BrepGen 将一个 B-rep 模型转换成一个三层的树状结构：实体 (Solid) -> 面 (Faces) -> 边 (Edges) -> 顶点 (Vertices)。 模型的几何与拓扑信息被精巧地编码在树的节点特征和结构中。

几何编码：节点特征 = 位置 + 局部形状

几何信息被存储为树中每个节点的特征向量。 该特征向量由两部分构成：全局位置和局部形状。

• 面 (Face): 一个面的几何由其所在的无限大的参数化曲面S(u,v):R2→R3S(u,v):\\mathbb{R}^2\\rightarrow \\mathbb{R}^3S(u,v):R2→R3定义。 为了将其表示为固定维度的特征，BrepGen 在该曲面的 UV 参数域上进行均匀网格采样，得到一个$N\times N$的3D点阵FsF_sFs​作为其局部形状的描述。 全局位置则由包围这些采样点的轴对齐包围盒（Bounding Box）FpF_pFp​表示。 随后，一个变分自编码器（VAE）将归一化后的点阵FsF_sFs​压缩成一个低维的潜在向量FzF_zFz​。因此，一个面节点的最终特征为F=[Fp,Fz]F=[F_p,F_z]F=[Fp​,Fz​]。
• 边 (Edge): 边的处理方式与面类似。其几何由参数化曲线C(u):R→R3C(u):\\mathbb{R}\\rightarrow \\mathbb{R}^3C(u):R→R3定义。沿曲线U轴采样N个点得到EsE_sEs​，并用包围盒EpE_pEp​表示其位置。 同样通过一个VAE压缩成潜在向量EzE_zEz​，最终边的特征为E=[Ep,Ez]E=[E_p,E_z]E=[Ep​,Ez​]。
• 顶点 (Vertex): 顶点最为简单，其特征就是它的三维坐标$(x,y,z)$。

层级 位置 𝐹p/𝐸p𝐹_p/𝐸_pFp​/Ep​ 局部形状 𝐹z/𝐸z𝐹_z/𝐸_zFz​/Ez​ 采样策略 Face 包围盒 [x₁,y₁,z₁,x₂,y₂,z₂][x_₁,y_₁,z_₁,x_₂,y_₂,z_₂][x₁​,y₁​,z₁​,x₂​,y₂​,z₂​] $N\times N$ UV 采样点 → 2D UNet VAE 压缩到 $4\times 4\times 3$ $N=32$ Edge 包围盒六维 + umin,umaxu_{min},u_{max}umin​,umax​ $N$ 沿曲线采样点 → 1D UNet VAE 压缩到 $4\times 3$ $N=32$ Vertex 直接 $(x,y,z)$ — —

拓扑编码：双重节点复制（作者称 Duplication）

这是 BrepGen 最巧妙的设计。B-rep 中复杂的图拓扑结构通过节点复制 (Node Duplication) 这一机制被隐式地编码进树结构中。

1. Mating Duplication (邻接复制)——为 共享 元素复制一份特征到每个父节点下：

   两个面共边 → 边节点出现两次；T 型三边共点 → 该顶点出现六次。

   这样，原始的图（Graph）结构就被转换成了一个树（Tree）结构。 在生成后，通过检测和合并具有相似特征的节点，即可恢复出邻接拓扑关系。

2. Association Duplication (关联复制)——为 填充到定长（神经网络需要固定长度的输入） 随机复制子节点，避免零填充引入无意义 token。在生成后，通过移除同一父节点下具有相同几何特征的子节点，即可恢复出唯一的关联关系

为什么“特征重复”就能在后处理里恢复邻接关系？

B-rep 中一条真实物理边被两个面共享；在树里它被 复制两份，特征几何上几乎一致。推理时用阈值聚类把“几何极近似”的节点合并，即可识别“我俩其实是同一条边”，天然得到面-边-面邻接关系。

合并规则：生成后若两节点包围盒距离 < 0.08 且解码点云 Chamfer < 0.2，则认定为同一实体并合并。

复制 + 阈值合并把离散拓扑预测化为“几何聚类”，回避了组合爆炸，同时允许网络在 [-3, 3] 归一化空间内只需精度到 0.05。

Association Duplication 相对零填充带来了什么实用好处？

相比零填充，它：

1. 保持 token 全是“真实几何”→ 网络不会学到无意义 0 向量；
2. 训练时随机复制可视作数据增广，降低过拟合；
3. 推理时易于用“同父节点且几何相同”快速剪枝恢复变长孩子。

生成模型：四级条件扩散

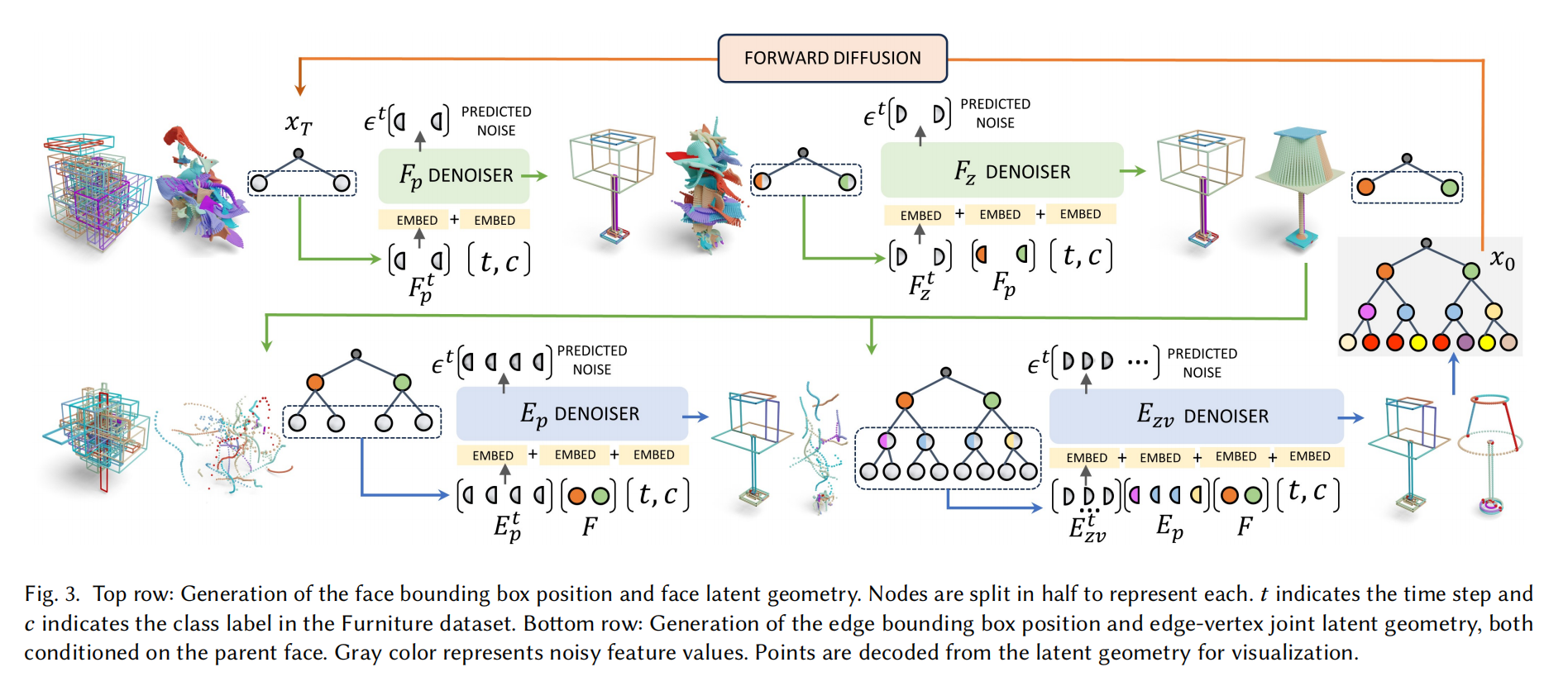
BrepGen 的整体架构可以概括为“树化表示 × 四级扩散”：它先把任意 B-rep 拆成固定宽度的三层树——面、边、顶点——每个节点特征由全局位置包围盒与经 VAE 压缩的局部形状潜码拼接而成；复杂拓扑则通过在树中复制共享元素隐式编码。生成阶段沿树自顶向下串行执行四个条件扩散子任务：①无条件去噪面的位置 Fₚ；②在 Fₚ 已确定的条件下去噪面的形状潜码 F_z；③以面特征 F 为父 token，通过简单的“token 加法”注入条件，去噪各条边的位置 Eₚ；④再以 F 和 Eₚ 为条件，去噪边-顶点联合形状潜码 E_{zv}。四个子网共享一套轻量 Transformer 骨干，时步 t 和类别 c 嵌入到每个 token 内。推理时，在第三阶段开始即用几何阈值做早期剪枝并在最终输出前合并重复节点，从而显式恢复邻接拓扑并生成 watertight 的 B-rep 实体。

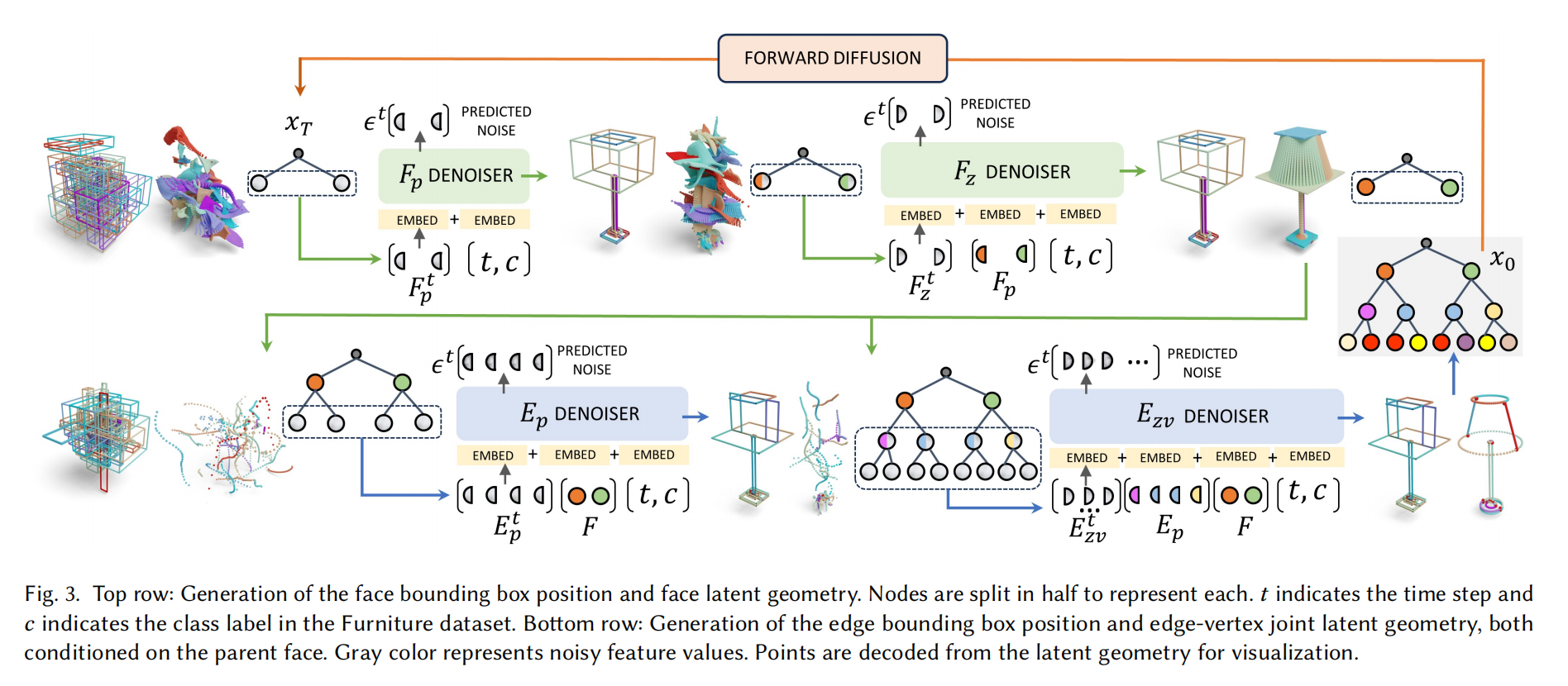
前向噪声

与标准 DDPM 一样，该过程在 $T$ 个时间步内，逐渐向树中所有节点的特征向量 x0x_0x0​ 添加高斯噪声，直至其变为纯粹的噪声 xTx_TxT​。 任意时刻 $t$ 的噪声数据 xtx_txt​ 可以通过以下公式直接采样得到：
q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I),xt=αˉtx0+1−αˉt ϵt,\\begin{align*}q(\\mathbf{x}_t | \\mathbf{x}_0) &= \\mathcal{N}(\\mathbf{x}_t; \\sqrt{\\bar{\\alpha}_t} \\mathbf{x}_0, (1 - \\bar{\\alpha}_t) \\mathbf{I}), \\\\\\mathbf{x}_t &= \\sqrt{\\bar{\\alpha}_t} \\mathbf{x}_0 + \\sqrt{1 - \\bar{\\alpha}_t} \\, \\boldsymbol{\\epsilon}_t,\\end{align*}q(xt​∣x0​)xt​​=N(xt​;αˉt​​x0​,(1−αˉt​)I),=αˉt​​x0​+1−αˉt​​ϵt​,​
其中ϵt\\boldsymbol{\\epsilon}_tϵt​是标准高斯噪声，αˉt\\bar{\\alpha}_tαˉt​是预设的噪声调度系数。

反向去噪——自顶向下四阶段

这是模型的生成阶段。BrepGen 并不一次性地对整棵树进行去噪，而是采用一种序列化、自顶向下的去噪策略。 这种策略将联合概率分布 $p(x)$ 分解为一系列条件概率的乘积：
p(x)=p(F,E,V)=p ⁣(Ezv∣Ep,F)⏟④ 边 + 顶点形状  p ⁣(Ep∣F)⏟③ 边位置  p ⁣(Fz∣Fp)⏟② 面形状  p ⁣(Fp∣∅)⏟① 面位置% 整体联合分布，等价记作 p(\\mathbf{x})p(\\mathbf{x})=p(F,E,V) = \\underbrace{p\\!\\left(E_{zv}\\mid E_{p},F\\right)}_{\\text{④~边 + 顶点形状}} \\;\\underbrace{p\\!\\left(E_{p}\\mid F\\right)}_{\\text{③~边位置}} \\;\\underbrace{p\\!\\left(F_{z}\\mid F_{p}\\right)}_{\\text{②~面形状}} \\;\\underbrace{p\\!\\left(F_{p}\\right| \\emptyset)}_{\\text{①~面位置}}p(x)=p(F,E,V)=④ 边 + 顶点形状p(Ezv​∣Ep​,F)​​③ 边位置p(Ep​∣F)​​② 面形状p(Fz​∣Fp​)​​① 面位置p(Fp​∣∅)​​

其中 EzvE_{zv}Ezv​ 是边和其关联顶点的联合特征。

这个分解意味着整个去噪过程由四个独立的、基于 Transformer 的去噪网络级联完成：

1. 第一阶段，无条件（网络只看时间 t 与类别 c）地生成面的位置特征 FpF_pFp​。
2. 然后，以生成的 FpF_pFp​ 为条件，生成面的形状潜码 FzF_zFz​。
3. 接着，以生成的面特征 F=[Fp,Fz]F=[F_p,F_z]F=[Fp​,Fz​] 为条件，生成其子节点（边）的位置特征 EpE_pEp​。
4. 最后，以面特征 $F$ 和边的位置特征 EpE_pEp​ 为条件，生成边和顶点的联合形状潜码 EzvE_{zv}Ezv​。

在每一步条件生成中，条件信息通过简单的令牌加法 (token addition) 注入：父面 token 通过逐 token 加法注入，而非 cross-attention；同时将边的两个顶点拼入同一 token，减少层级深度。。

例如，在生成边 $j$ 的特征时，其父节点（面 $i$）的特征令牌会直接加到边 $j$ 的特征令牌上：E^p,j←Ep,j+Fi\\hat{E}_{p,j} \\leftarrow E_{p,j} + F_iE^p,j​←Ep,j​+Fi​。

模型的训练目标是标准的 L2 回归损失：L=Et,x0,ϵt[∥ϵt−ϵθ(xt,t)∥2]L = \\mathbb{E}_{t, \\mathbf{x}_0, \\boldsymbol{\\epsilon}_t} \\left[ \\left\\| \\boldsymbol{\\epsilon}_t - \\boldsymbol{\\epsilon}_\\theta \\left(x_t, t \\right) \\right\\|^2 \\right]L=Et,x0​,ϵt​​[∥ϵt​−ϵθ​(xt​,t)∥2]，即预测每一步所添加的噪声。

相比“同时生成所有节点”，这种分阶段去噪有什么好处？

1. 先固定 父级位置，再生成更细粒度的形状，可显著缩小搜索空间；
2. 条件化链条把长依赖显式拆开，Transformer 只需学习局部一致性而非全局同时满足，从而更稳定、收敛更快 — 作者消融显示两段式生成有效率↑20%。

为什么作者不把“顶点位置”单列为第五阶段？

顶点坐标已拼进 EzvE_{zv}Ezv​ token；顶点与边一一对应（每边恰两端点）。再做第五阶段只会重复复制，浪费显存且放大误差。

采样与早期剪枝

• 采样步长 1000 → (可控速度：A50004 显存够用)。
• 在第三阶段生成边位置时就开始 Early Pruning，即对子树局部做合并，减少后续冗余。

B-rep 后处理：从树到 CAD

1. Association Merge：同父节点下重复元素先合并。
2. Mating Merge：跨父节点找到几何相同的元素，恢复邻接关系。
3. 几何微调：
   • 顶点取平均；
   • 边点云刚性配准到端点；若方向反了则整体翻转；
   • 在 Chamfer 最小化下微调面网格。
4. B-rep 输出：trim face → sew faces → solid。

实验要点

• 数据：DeepCAD (66 k), ABC (1 M)，新增 Furniture 6 k（10 类，最多 450+ 面/体）。
• 指标：Coverage/MMD/JSD + Valid Ratio。
• 定量分析: 与之前的 SOTA 方法 DeepCAD 和 SolidGen 相比，BrepGen 在多项分布度量指标（如覆盖率 COV、最小匹配距离 MMD、JSD 散度）上均取得了显著优势，表明其生成的模型在质量和分布上都更接近真实数据。 同时，其生成的有效（watertight）模型比例也更高。
• 定性分析: 可视化结果显示，BrepGen 能够生成结构复杂、拓扑正确且包含平滑自由曲面的高质量 CAD 模型，其真实感和多样性远超以往方法。
• 可控生成: 论文还展示了 BrepGen 在可控生成方面的强大潜力，包括：
  • 类别条件生成: 根据给定的类别标签（如“椅子”、“桌子”）生成对应的家具模型。
  • CAD 自动补全: 仅给出模型的部分面片，BrepGen 能够合理地“脑补”出完整的几何与拓扑结构。
  • 设计插值: 在两个给定的 CAD 模型之间，生成一系列平滑过渡的中间设计。
• 消融：
  • 去掉 Association Duplication → 面/边缺失↑ 21%；
  • 无 Early Pruning → GPU 占用 ↑ 1.7×。
• 失败案例：缺面、曲面自交、抖动几何（见 Fig. 15）。

创新点

关键词 本质突破 影响 SLG Tree 图→树，离散拓扑→连续几何聚类，支持 任意曲面 统一输入长度，把图问题降维 双复制策略 Topology + Padding 一举两得 探索空间大大缩小 4-Stage Latent Diffusion “位置→形状”解耦，父-子条件化 去噪难度分层，收敛稳定 早期剪枝 + Heuristic 合并 训练时无拓扑标签，推理靠阈值重建 通用但留有 0.05 精度上限 Furniture B-rep Dataset Free-form + 分类标签 下游可控生成基准

不足和展望

总结: BrepGen 是 CAD 智能生成领域的一项里程碑式的工作。它通过提出一种精巧的结构化树表示，成功地解决了直接生成复杂 B-rep 模型这一长期存在的难题。实验结果充分证明了该方法在生成质量、多样性和可控性方面的优越性，将 B-rep 生成技术推向了一个新的高度，向着实现真正的“自动化设计”迈出了坚实的一步。

展望与局限: 尽管成就斐然，作者也指出了该方法的局限性和未来方向：

• 多实体装配: 目前 BrepGen 仅支持生成单个实体（solid body），无法处理由多个零件装配而成的复杂产品。
• 无法保证水密性: 尽管有效率很高，但生成过程本质上是概率性的，无法 100% 保证输出是水密的。
• 启发式后处理: 目前的拓扑恢复依赖于启发式的阈值判断，一个基于学习的、更鲁棒的后处理模块是值得探索的方向。
• 精度限制: 基于阈值的节点合并策略意味着模型对距离过近的精细结构不敏感。

未来的工作可以在这些方面进行深化，例如将 BrepGen 扩展到装配体生成，或者研究端到端的、能保证拓扑有效性的生成框架。

局限性：

• 仅单 Solid——装配体仍需从零件级递归生成。
• 水密性非保证——依赖阈值，25% 概率仍有缝或自交。
• 阈值精度上限——0.05 单位导致微细结构被合并。

方向：后处理启发式——作者建议未来做基于学习的、更鲁棒的后处理模块。

如果要支持 装配体，是加一层 “Body” 节点还是多树并行更合理？

多 Body 装配常有跨零件配准与约束；直接加“Body”层仍是单树，不便表达 跨 Body 依赖。更合理做法：多树并行 + 顶层装配图，把每个零件各自生成，再用额外图网络预测定位 / 接口，对独立性与复用更友好。

平面设计问答解答