网站导航
> 技术文档 > 数学建模——蚁群算法_蚁群优化算法实现步骤

数学建模——蚁群算法_蚁群优化算法实现步骤

网友: 技术文档 2025-09-03 09:48:12

1.概念

蚁群算法（Ant Colony Optimization, ACO）是一种模拟蚂蚁觅食行为的群体智能优化算法，由Marco Dorigo于1992年提出。它通过信息素（pheromone）的正反馈机制和启发式搜索来解决组合优化问题（如TSP、路径规划、调度等）。

名词解释

信息素 蚂蚁释放的化学物质，其他蚂蚁可以感知到 浓度越高其他蚂蚁越容易选择 启发式信息 指与问题领域相关的先验知识或经验规则，用于引导蚂蚁的搜索方向，提高算法效率和解的质量。 指导蚂蚁选择下一步的方向 路径构建 蚂蚁从随机的一个起点开始根据信息素浓度和启发式信息的综合影响选择下一步，直到构建出完整的解决方案 由信息素浓度和启发式信息决定 信息素更新 每一轮结束后蚂蚁会根据路径更新信息素 更好的方案信息素浓度更大 其他地方信息素挥发避免陷入局部最优

 关键参数

参数 解释 作用 取值 信息素因子\\alpha 控制信息素对路径选择的影响程度

过高 

  • 机制：
    蚂蚁过度依赖信息素，即使当前路径是局部最优，也会因高浓度信息素被持续强化，压制新路径的探索。

  • 表现：
    算法过早收敛，所有蚂蚁集中到一条次优路径，无法跳出（如TSP中卡在“绕远路”的环路）。

0~5

过低 

  • 机制：
    蚂蚁几乎忽略信息素，完全依赖启发式信息（如距离倒数），导致短视的贪心决策。

  • 表现：
    算法像“贪心算法”，每一步选局部最优，但全局可能很差（如TSP中形成交叉路径）。

启发函数因子\\beta 控制的是启发式信息（η）对蚂蚁决策的影响强度。它和信息素因子（α）是一对互补的“调节阀”

过高

表现：蚂蚁过度依赖启发式信息（如距离倒数），几乎忽略信息素。
后果：

  • 算法退化为贪心算法：每一步都选“当前看起来最好”的选项，但全局可能很差。

  • 早熟收敛到局部最优：比如TSP中形成交叉路径或“短视环路”。

  • 丧失群体学习能力：信息素无法积累，蚂蚁各自为战。

类比：像没有社会协作的蚂蚁，每只都自私地选最近食物，导致整体效率低下。

0~10

过低 

表现：蚂蚁几乎忽略启发式信息，完全依赖信息素做决策。
后果：

  • 搜索盲目：蚂蚁像“无头苍蝇”，只跟风信息素，可能绕远路。

  • 收敛极慢：缺乏启发式引导，探索效率低。

  • 难以跳出局部最优：信息素主导的“历史路径”被盲目强化。

类比：像一群蚂蚁不看地形（距离、成本），只凭“前人脚印”走，可能集体绕大圈。

信息素挥发因子\\rho 信息素挥发因子（ρ，rho）是蚁群算法（ACO）中唯一“做减法”的参数——它决定每一轮迭代后保留多少旧信息素。

过高

信息素挥发极快，“记忆力”差。刚发现一条好路，转身就忘，下次从头再来。丢失了有效路径

0~1

常取值0.1

过低 

信息素挥发极慢，“记忆力”强。难以排除无效路径，“有些不需要记住的也都记住了”，而且还会影响收敛速度

信息素总量Q 通常表示每只蚂蚁在每次迭代中释放的信息素量

值越大信息素更新越明显

值过小会削弱挥发因子的作用

 参数之间的关系：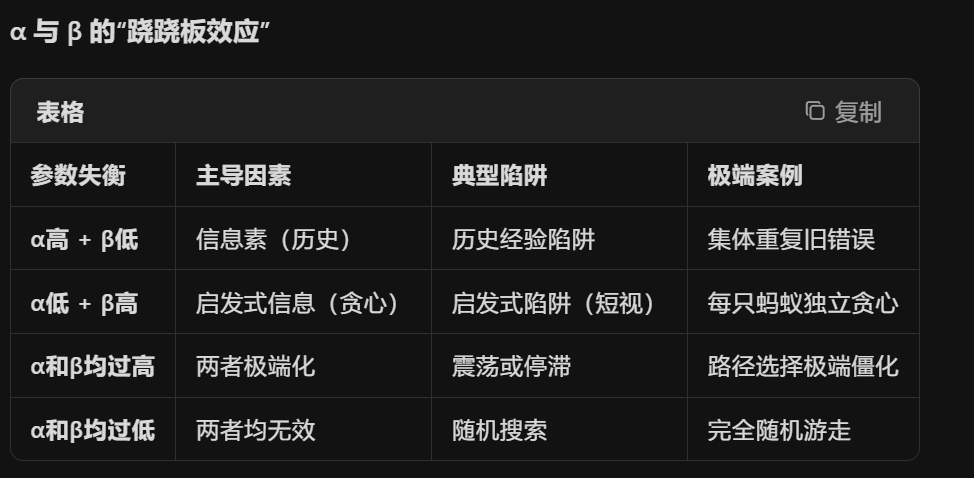

*初期：我们希望蚂蚁多走动，且启发式信息在初期对路径选择更有帮助

所以初期\\beta取值高一点，\\alpha取值低一点

核心原理

  1. 蚂蚁行为模拟

    • 蚂蚁在觅食时会释放信息素，路径上的信息素浓度越高，后续蚂蚁选择该路径的概率越大。

    • 信息素会随时间挥发（避免陷入局部最优）。

  2. 算法关键要素

    • 信息素更新：

      • 挥发：所有路径的信息素按一定比例减少（避免过早收敛）。

      • 增强：优质路径（如更短的路线）会被更多蚂蚁强化信息素。

    • 概率选择：蚂蚁根据信息素浓度和启发式信息（如路径长度）选择下一步。

选择概率公式 

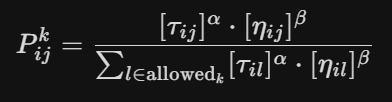
 P_{ij}^k = \\frac{[\\tau_{ij}]^\\alpha \\cdot [\\eta_{ij}]^\\beta}{\\sum_{l \\in \\mathcal{N}_i^k} [\\tau_{il}]^\\alpha \\cdot [\\eta_{il}]^\\beta}

  • \\tau_{ij} 是路径 (i, j) 上的信息素浓度；

  • \\eta_{ij} 是启发式信息（如距离的倒数）；

  • \\alpha 是信息素因子；

  • \\beta 是启发函数因子；

  • \\mathcal{N}_i^k \\; or\\; \\textup{allowed}_k 是蚂蚁 k 在城市 i 的可行邻域。

2.代码实现

1.初始化数据

比如城市坐标，城市数量，蚂蚁数量，最大迭代次数，信息素因子，启发函数因子，挥发系数等

初始化信息素矩阵记录每个城市间的信息素浓度，距离矩阵记录城市间距离

city=[1038, 435; 836, 303; 867, 593; 515, 37; 298, 116; 513, 435; 547, 592; 247, 640; 113, 499; 211, 349; 98, 163; 59, 38];city=city/2;num_city=size(city,1);num_ants=24;max_iter=50;alpha=1;beta=2;rho=0.6;Q=100;%初始化信息素矩阵和距离矩阵pheromone=ones(num_city);distance=zeros(num_city);%计算城市之间的距离，自己和自己之间的距离是无穷大for i=1:num_city for j=1:num_city if i~=j distance(i,j)=sqrt(sum((city(i,:)-city(j,:)).^2)); else distance(i,j)=inf; end endend

2.主函数

主函数相对比较复杂

核心目标是让每一只蚂蚁都根据信息素和启发函数因子走一条路出来，然后再选最好的路

这里点两个细节

1.概率计算公式

probabilities(j)=(pheromone(current_city,j)^alpha)*(1/distance(current_city,j)^beta);%计算概率

这里实际需要根据情况调节\\alpha和\\beta的比例，让两者不要差距太大，否则会陷入局部最优

2.快速计算距离

怎么快速计算环的距离？

假设路径是2 4 3 1 5，那就要计算2——>4——>3——>1——>5——>2

所以我取2 4 3 1 5的后四个4 3 1 5 再把2拼在最后变成4 3 1 5 2

这样每次找这两个数组对应位置就是连线的首尾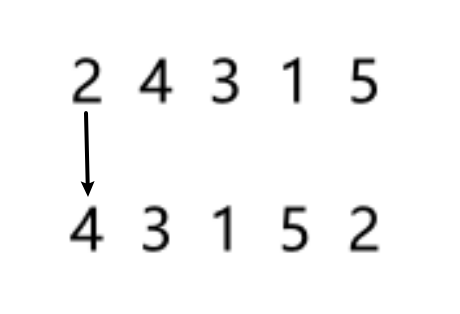

%主循环best_length=inf;%初始化最大距离是无穷大best_route=[];%初始化矩阵用来记录最短路径figure;for iter =1:max_iter%外层循环，总迭代次数100次 routes=zeros(num_ants,num_city);%给所有蚂蚁都创建一个最佳路径矩阵 route_lengths=zeros(num_ants,1);%记录每一只蚂蚁的最短路径长度 for k=1:num_ants%第二次循环遍历每一只蚂蚁 route=zeros(1,num_city);%创建初始路径 route(1)=randi(num_city);%随机选择一个城市作为起点 for step=2:num_city%第三层循环用来计算每一只蚂蚁后面的剩余路径 current_city=route(step-1);%记录当前城市 probabilities=zeros(1,num_city);%初始化可行矩阵 for j=1:num_city%第四层循环计算没有到达城市的概率 if ~ismember(j,route(1:step-1))%假如城市未到达  probabilities(j)=(pheromone(current_city,j)^alpha)*(1/distance(current_city,j)^beta);%计算概率 end end probabilities=probabilities/sum(probabilities);%归一化概率 next_city=randsample(1:num_city,1,true,probabilities);%根据前面的概率选择下一个城市，根据概率赌 route(step)=next_city;%填入赌中的城市 end routes(k,:)=route;%存入所有路径 route_lengths(k)=sum(arrayfun(@(x,y) distance(x,y),route,[route(2:end),route(1)]));%计算回路总距离 end [min_length,min_index]=min(route_lengths);%最短路径和其对应的索引 if min_length < best_length%比最优路径短，更新 best_length=min_length; best_route = routes(min_index,:); end pheromone=pheromone*(1-rho);%信息素挥发 for k=1:num_ants for step =1:num_city from= routes(k,step); to=routes(k,mod(step,num_city)+1); pheromone(from,to)=pheromone(from,to)+Q/route_lengths(k);%路径越短，delta越大，鼓励更多蚂蚁以后走这条边。 pheromone(to,from)=pheromone(to,from)+Q/route_lengths(k); end end

3.整体代码

%蚁群算法function Ants()city=[1038, 435; 836, 303; 867, 593; 515, 37; 298, 116; 513, 435; 547, 592; 247, 640; 113, 499; 211, 349; 98, 163; 59, 38];city=city/2;num_city=size(city,1);num_ants=24;max_iter=50;alpha=1;beta=2;rho=0.6;Q=100;%初始化信息素矩阵和距离矩阵pheromone=ones(num_city);distance=zeros(num_city);%计算城市之间的距离，自己和自己之间的距离是无穷大for i=1:num_city for j=1:num_city if i~=j distance(i,j)=sqrt(sum((city(i,:)-city(j,:)).^2)); else distance(i,j)=inf; end endend%主循环best_length=inf;%初始化最大距离是无穷大best_route=[];%初始化矩阵用来记录最短路径figure;for iter =1:max_iter%外层循环，总迭代次数100次 routes=zeros(num_ants,num_city);%给所有蚂蚁都创建一个最佳路径矩阵 route_lengths=zeros(num_ants,1);%记录每一只蚂蚁的最短路径长度 for k=1:num_ants%第二次循环遍历每一只蚂蚁 route=zeros(1,num_city);%创建初始路径 route(1)=randi(num_city);%随机选择一个城市作为起点 for step=2:num_city%第三层循环用来计算每一只蚂蚁后面的剩余路径 current_city=route(step-1);%记录当前城市 probabilities=zeros(1,num_city);%初始化可行矩阵 for j=1:num_city%第四层循环计算没有到达城市的概率 if ~ismember(j,route(1:step-1))%假如城市未到达  probabilities(j)=(pheromone(current_city,j)^alpha)*(1/distance(current_city,j)^beta);%计算概率 end end probabilities=probabilities/sum(probabilities);%归一化概率 next_city=randsample(1:num_city,1,true,probabilities);%根据前面的概率选择下一个城市，根据概率赌 route(step)=next_city;%填入赌中的城市 end routes(k,:)=route;%存入所有路径 route_lengths(k)=sum(arrayfun(@(x,y) distance(x,y),route,[route(2:end),route(1)]));%计算回路总距离 end [min_length,min_index]=min(route_lengths);%最短路径和其对应的索引 if min_length < best_length%比最优路径短，更新 best_length=min_length; best_route = routes(min_index,:); end pheromone=pheromone*(1-rho);%信息素挥发 for k=1:num_ants for step =1:num_city from= routes(k,step); to=routes(k,mod(step,num_city)+1); pheromone(from,to)=pheromone(from,to)+Q/route_lengths(k);%路径越短，delta越大，鼓励更多蚂蚁以后走这条边。 pheromone(to,from)=pheromone(to,from)+Q/route_lengths(k); end end clf; plot(city(:,1),city(:,2),\'bo\'); hold on; best_route_cities=[best_route,best_route(1)]; for i=1:num_city from=best_route_cities(i); to=best_route_cities(i+1); quiver(city(from,1),city(from,2),city(to,1)-city(from,1),city(to,2)-city(from,2),0,\'color\',[0.5 0.75 1],\'MaxHeadSize\',0.2); %quiver(x0, y0, dx, dy, scale, \'属性名\', 属性值, ...) end start_city=best_route(1); end_city=best_route(end); plot(city(start_city,1),city(start_city,2),\'go\',\'MarkerSize\',8,\'MarkerFaceColor\',\'g\'); plot(city(end_city,1),city(end_city,2),\'ro\',\'MarkerSize\',8,\'MarkerFaceColor\',\'r\'); text(city(start_city,1),city(start_city,2),\'起点\',\'VerticalAlignment\',\'bottom\',\'HorizontalAlignment\',\'left\'); text(city(end_city,1),city(end_city,2),\'终点\',\'VerticalAlignment\',\'bottom\',\'HorizontalAlignment\',\'left\'); for i=1:num_city text(city(i,1),city(i,2),sprintf(\'City %d\',i),\'VerticalAlignment\',\'bottom\'); end title(sprintf(\'Iteration %d: Best length= %.2f\',iter,best_length)); xlabel(\'X\'); ylabel(\'Y\'); grid on; hold off; pause(0.1);endfsprintf(\'Best route:\');disp(best_route);fsprintf(\'Best length: %.2f\\n\',best_length);end
网络标签：

相关问题