面试必知！DFS、回溯、设计代码高频题大揭秘

技术文档

一、引言

在程序员面试的激烈竞争中，掌握代码高频题是脱颖而出的关键。代码高频题涵盖多种题型，每种题型都有其独特的解题思路和技巧。按题型分类学习，能让我们更系统地掌握解题方法，提高面试成功率。在众多题型中，深度优先搜索（DFS）、回溯算法和设计类题目是高频考点，它们不仅考察编程基础，更考验逻辑思维和问题解决能力。接下来，我们就一起深入剖析这三类题型。

二、DFS 题型

（一）DFS 算法基础

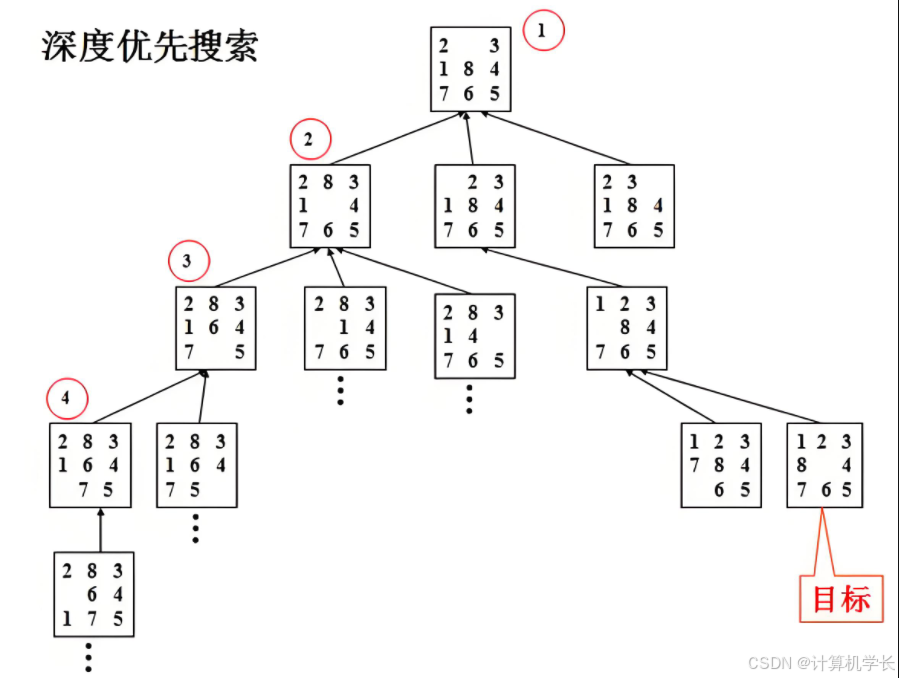
深度优先搜索（DFS, Depth-First Search）是一种用于遍历或搜索树或图的算法。它沿着树的深度遍历树的节点，尽可能深地探索每一条分支，当节点的所有子节点都被访问过后，再回溯到父节点继续搜索其他分支。在二叉树中，DFS 的实现通常通过递归完成，常见的二叉树 DFS 遍历方式有前序遍历、中序遍历和后序遍历。

以二叉树前序遍历为例，其代码实现如下（Python）：

class TreeNode:

def __init__(self, val=0, left=None, right=None):

self.val = val

self.left = left

self.right = right

def preorderTraversal(root):

result = []

if root:

result.append(root.val)

result += preorderTraversal(root.left)

result += preorderTraversal(root.right)

return result

# 示例用法

root = TreeNode(1)

root.right = TreeNode(2)

root.right.left = TreeNode(3)

print(preorderTraversal(root)) # 输出: [1, 2, 3]

在这段代码中，preorderTraversal函数首先访问根节点，然后递归地访问左子树，最后递归地访问右子树，体现了 DFS 的递归特性。

对于 N 叉树的 DFS 遍历，原理类似，但需要遍历每个子节点。以下是 N 叉树前序遍历的代码示例（Python）：

class Node:

def __init__(self, val=None, children=None):

self.val = val

self.children = children if children is not None else []

def preorder(root):

result = []

if root:

result.append(root.val)

for child in root.children:

result += preorder(child)

return result

# 示例用法

root = Node(1)

root.children = [Node(3), Node(2), Node(4)]

root.children[0].children = [Node(5), Node(6)]

print(preorder(root)) # 输出: [1, 3, 5, 6, 2, 4]

通过这两个例子可以看出，DFS 通过递归不断深入探索子节点，直到无法继续，然后回溯，这种特性使得它在处理需要深度探索的问题时非常有效。

（二）高频面试题讲解 - 岛屿数量

题目描述：给定一个由 \'1\'（陆地）和 \'0\'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。可以假设网格的四个边均被水包围。例如：

grid = [

[\"1\",\"1\",\"1\",\"1\",\"0\"],

[\"1\",\"1\",\"0\",\"1\",\"0\"],

[\"1\",\"1\",\"0\",\"0\",\"0\"],

[\"0\",\"0\",\"0\",\"0\",\"0\"]

]

输出为 1，因为只有一个岛屿。

2. 解题思路：可以将二维网格看成一个无向图，竖直或水平相邻的 1 之间有边相连。为了求出岛屿的数量，可以扫描整个二维网格。如果一个位置为 1，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0 ，这样可以避免重复计数。最终岛屿的数量就是进行深度优先搜索的次数。

3. 代码实现（Python）：

class Solution:

def dfs(self, grid, r, c):

grid[r][c] = \'0\'

nr, nc = len(grid), len(grid[0])

for x, y in [(r - 1, c), (r + 1, c), (r, c - 1), (r, c + 1)]:

if 0 <= x < nr and 0 <= y < nc and grid[x][y] == \'1\':

self.dfs(grid, x, y)

def numIslands(self, grid):

if not grid:

return 0

nr = len(grid)

nc = len(grid[0])

num_islands = 0

for r in range(nr):

for c in range(nc):

if grid[r][c] == \'1\':

num_islands += 1

self.dfs(grid, r, c)

return num_islands

# 测试

grid = [

[\"1\", \"1\", \"0\", \"0\", \"0\"],

[\"0\", \"0\", \"1\", \"0\", \"0\"],

[\"0\", \"0\", \"0\", \"1\", \"1\"]

]

solution = Solution()

print(solution.numIslands(grid)) # 输出: 3

代码解释：

dfs函数用于从位置(r, c)开始进行深度优先搜索，将访问过的陆地标记为 \'0\'。

numIslands函数遍历整个网格，每当遇到一个值为 \'1\' 的位置，就调用dfs函数，并将岛屿数量加 1。

复杂度分析：

时间复杂度：O (MN)，其中 M 和 N 分别为行数和列数。因为需要遍历整个二维网格，对每个位置最多进行一次访问。

空间复杂度：O (MN)，在最坏情况下，整个网格均为陆地，深度优先搜索的深度达到 MN，即递归调用栈的深度为 MN。

（三）高频面试题讲解 - 岛屿的最大面积

题目描述：给定一个包含了一些 0 和 1 的非空二维数组grid 。一个岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。可以假设grid的四个边缘都被 0（代表水）包围着。找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0。) 例如：

grid = [

[0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],

[0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],

[0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0],

[0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]

]

输出为 6，因为最大的岛屿面积为 6。

2. 解题思路：想知道网格中每个连通形状的面积，然后取最大值。如果在一个土地上，以 4 个方向探索与之相连的每一个土地（以及与这些土地相连的土地），那么探索过的土地总数将是该连通形状的面积。为了确保每个土地访问不超过一次，每次经过一块土地时，将这块土地的值置为 0。这样就不会多次访问同一土地。

3. 代码实现（Python）：

class Solution:

def dfs(self, grid, cur_i, cur_j):

if cur_i < 0 or cur_j < 0 or cur_i == len(grid) or cur_j == len(grid[0]) or grid[cur_i][cur_j] != 1:

return 0

grid[cur_i][cur_j] = 0

ans = 1

for di, dj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:

next_i, next_j = cur_i + di, cur_j + dj

ans += self.dfs(grid, next_i, next_j)

return ans

def maxAreaOfIsland(self, grid):

max_area = 0

for i, l in enumerate(grid):

for j, n in enumerate(l):

if n == 1:

max_area = max(self.dfs(grid, i, j), max_area)

return max_area

# 测试

grid = [

[0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],

[0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],

[0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0],

[0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],

[0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]

]

solution = Solution()

print(solution.maxAreaOfIsland(grid)) # 输出: 6

代码解释：

dfs函数用于计算从位置(cur_i, cur_j)开始的岛屿面积，通过递归向四个方向探索，将访问过的陆地标记为 0，并返回岛屿面积。

maxAreaOfIsland函数遍历整个网格，对每个值为 1 的位置调用dfs函数，记录并返回最大的岛屿面积。

复杂度分析：

时间复杂度：O (R * C)，其中 R 和 C 分别是给定二维数组的行数和列数。需要遍历数组中的每个元素，对每个元素最多进行一次深度优先搜索。

空间复杂度：O (R * C)，在最坏情况下，整个网格均为陆地，深度优先搜索的深度达到 R * C，即递归调用栈的深度为 R * C。

三、回溯题型

（一）回溯算法基础

回溯算法实际上是一个类似枚举的深度优先搜索尝试过程，是 DFS 的一种应用，它在每一次尝试中，通过不断地尝试各种可能的选择来找到问题的解。如果当前选择不符合要求，就撤销当前选择，回退到上一个状态，然后尝试其他选择，这就是 “回溯” 的含义。回溯算法的核心在于递归和回溯，递归用于深入探索问题的解空间，回溯则在发现当前路径无法得到有效解时，撤销之前的选择，回到之前的状态继续探索。

回溯算法的一般模板如下（Python）：

def backtracking(参数):

if 终止条件:

收集结果

return

for 选择 in 选择列表:

做选择

backtracking(新参数)

撤销选择 # 回溯

终止条件：定义什么时候停止递归，通常是找到一个满足条件的解或者遍历完所有可能的情况。比如在组合问题中，当选择的元素个数达到要求时，就找到了一个有效的组合，此时终止递归并收集结果。

选择列表：表示在当前状态下可以做出的所有选择。例如在从 1 - 5 中选择 3 个数的组合问题中，在初始状态下，选择列表就是 1、2、3、4、5 这 5 个数。

做选择：将当前选择的元素加入到结果集中，并且更新相关的状态变量。

递归调用：进入下一层递归，继续探索下一个状态。每一层递归都有自己的选择列表和当前状态。

撤销选择：在递归返回后，需要撤销之前做出的选择，以便尝试其他选择。这是回溯算法的关键步骤，通过撤销选择，算法可以回到上一个状态，从而尝试不同的路径。

（二）高频面试题讲解 - 组合

题目描述：给定两个整数n和k，返回范围[1, n]中所有可能的k个数的组合。例如，当n = 4，k = 2时，输出为[[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]] 。

解题思路：可以使用回溯算法来解决这个问题。回溯算法的核心思想是通过递归不断尝试各种可能的选择，当发现当前选择无法满足条件时，回溯到上一个状态，重新选择。对于组合问题，从集合中依次选取元素，每选取一个元素，就从剩余的元素中继续选取，直到选取了k个元素为止。为了避免重复选取，使用start_index来记录当前搜索的起始位置，每次递归时，从start_index开始往后搜索。同时，可以通过剪枝优化来提高效率，当剩余元素个数小于需要选取的元素个数时，直接返回，不再继续递归。

代码实现（Python）：

def combine(n, k):

result = []

path = []

def backtracking(n, k, start_index):

if len(path) == k:

result.append(path[:])

return

for i in range(start_index, n - (k - len(path)) + 2):

path.append(i)

backtracking(n, k, i + 1)

path.pop()

backtracking(n, k, 1)

return result

# 测试

n = 4

k = 2

print(combine(n, k)) # 输出: [[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

代码解释：

combine函数初始化结果列表result和路径列表path，并调用backtracking函数开始回溯。

backtracking函数中，当path的长度等于k时，说明找到了一个满足条件的组合，将其加入result中并返回。

for循环从start_index开始遍历，每次将当前元素加入path，然后递归调用backtracking，传入更新后的start_index（即i + 1）。递归返回后，将当前元素从path中移除，进行回溯。

在for循环中，range的上限使用了剪枝优化，n - (k - len(path)) + 2表示剩余元素个数至少要满足选取的要求，这样可以减少不必要的递归。

复杂度分析：

时间复杂度：\\(O(C_{n}^{k} \\times k)\\)，其中\\(C_{n}^{k}\\)是组合数，表示从n个元素中选取k个元素的组合数量，计算每个组合需要O(k)的时间来复制到结果集中。

空间复杂度：\\(O(k)\\)，除了返回结果外，空间复杂度主要取决于递归调用栈的深度和path列表的大小，在最坏情况下，递归深度为k，path列表的大小也为k。

（三）高频面试题讲解 - 复原 IP 地址

题目描述：给定一个只包含数字的字符串s，复原它并返回所有可能的有效 IP 地址。有效 IP 地址正好由四个整数（每个整数位于0到255之间组成，且不能含有前导0），整数之间用\'.\'分隔。例如，输入s = \"25525511135\"，输出为[\"255.255.11.135\", \"255.255.111.35\"] 。

解题思路：通过回溯算法来解决，设计一个递归函数，在递归过程中，每次从字符串中截取一段数字，判断其是否合法（在0到255之间且没有前导0，除非数字本身是0），如果合法，则将其作为 IP 地址的一段，并继续递归处理剩余的字符串。在递归过程中，需要记录当前已经处理的段数，如果已经处理了 4 段，且字符串已经全部处理完，则找到了一个有效的 IP 地址。为了提高效率，可以进行剪枝处理，例如当剩余的字符数量大于剩余段数的 3 倍时，说明无法构成有效的 IP 地址，直接返回。

代码实现（Python）：

def restoreIpAddresses(s):

result = []

def backtracking(s, start_index, path, segment_count):

if segment_count == 4:

if start_index == len(s):

result.append(\'.\'.join(path))

return

for i in range(1, 4):

end_index = start_index + i

if end_index > len(s):

break

segment = s[start_index:end_index]

if (segment[0] == \'0\' and len(segment) > 1) or int(segment) > 255:

break

path.append(segment)

backtracking(s, end_index, path, segment_count + 1)

path.pop()

backtracking(s, 0, [], 0)

return result

# 测试

s = \"25525511135\"

print(restoreIpAddresses(s)) # 输出: [\"255.255.11.135\", \"255.255.111.35\"]

代码解释：

restoreIpAddresses函数初始化结果列表result，并调用backtracking函数开始回溯。

backtracking函数中，start_index表示当前处理的起始位置，path列表用于存储已经处理的 IP 地址段，segment_count表示已经处理的段数。

当segment_count等于 4 时，如果start_index也等于字符串的长度，说明找到了一个有效的 IP 地址，将其加入result中。

for循环中，i从 1 到 3，表示每次截取 1 到 3 个字符作为一段。判断截取的段是否合法，如果不合法则直接break。如果合法，则将其加入path，继续递归处理剩余的字符串。递归返回后，将当前段从path中移除，进行回溯。

复杂度分析：

时间复杂度：在爆搜的情况下，由于 IP 地址最多有 4 段，每段最多有 3 种选择（1 个字符、2 个字符、3 个字符），所以时间复杂度为\\(O(3^4)\\)，但实际上通过剪枝操作，时间复杂度会远小于这个值。

空间复杂度：\\(O(1)\\)，除了返回结果外，空间复杂度主要取决于递归调用栈的深度，在最坏情况下，递归深度为 4，所以空间复杂度为\\(O(1)\\) 。

四、设计题型

（一）设计类问题特点

设计类问题在面试中侧重于考察候选人对数据结构的理解和运用能力，以及对复杂系统的抽象建模能力。这类问题通常没有固定的模板，需要根据具体的需求来设计合适的数据结构和算法。解决设计类问题的关键在于准确理解需求，选择合适的数据结构，优化操作的时间复杂度和空间复杂度。例如，在设计缓存系统时，需要考虑如何快速地获取和插入数据，以及如何在缓存满时淘汰最少使用的数据；在设计队列时，要考虑如何高效地实现入队和出队操作，以及如何处理队列的边界情况。

（二）高频面试题讲解 - 最小栈

题目描述：设计一个支持push、pop、top操作，并能在常数时间内检索到最小元素的栈。具体操作如下：

push(x)：将元素x推入栈中。

pop()：删除栈顶的元素。

top()：获取栈顶元素。

getMin()：检索栈中的最小元素。

解题思路：为了实现getMin操作的时间复杂度为 O (1)，可以使用一个辅助栈来同步存储每个状态下的最小值。每次push操作时，将元素x压入数据栈，同时比较x与辅助栈栈顶元素的大小，如果x小于等于辅助栈栈顶元素，则将x也压入辅助栈；每次pop操作时，如果数据栈弹出的元素等于辅助栈栈顶元素，则辅助栈也弹出栈顶元素；top操作直接返回数据栈栈顶元素；getMin操作直接返回辅助栈栈顶元素。

代码实现（Python）：

class MinStack:

def __init__(self):

self.data_stack = []

self.min_stack = []

def push(self, x):

self.data_stack.append(x)

if not self.min_stack or x <= self.min_stack[-1]:

self.min_stack.append(x)

def pop(self):

if self.data_stack:

if self.data_stack[-1] == self.min_stack[-1]:

self.min_stack.pop()

self.data_stack.pop()

def top(self):

if self.data_stack:

return self.data_stack[-1]

def getMin(self):

if self.min_stack:

return self.min_stack[-1]

# 测试

min_stack = MinStack()

min_stack.push(-2)

min_stack.push(0)

min_stack.push(-3)

print(min_stack.getMin()) # 输出: -3

min_stack.pop()

print(min_stack.top()) # 输出: 0

print(min_stack.getMin()) # 输出: -2

代码解释：

__init__方法初始化数据栈data_stack和辅助栈min_stack。

push方法将元素x压入数据栈，同时根据条件将x压入辅助栈。

pop方法弹出数据栈栈顶元素，并根据条件弹出辅助栈栈顶元素。

top方法返回数据栈栈顶元素。

getMin方法返回辅助栈栈顶元素。

复杂度分析：

时间复杂度：push、pop、top和getMin操作的时间复杂度均为 O (1)，因为它们都只涉及栈的基本操作，没有循环或递归。

空间复杂度：O (n)，其中 n 是栈中元素的个数。在最坏情况下，辅助栈的大小与数据栈相同。

（三）高频面试题讲解 - LRU 缓存机制

题目描述：运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作：获取数据get和写入数据put 。

获取数据get(key)：如果密钥(key)存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。

写入数据put(key, value)：如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

解题思路：使用双向链表和哈希表来实现 LRU 缓存。双向链表用于维护元素的访问顺序，哈希表用于快速定位元素在双向链表中的位置。具体来说，每次访问一个元素时，将其从链表中删除并移动到链表头部，表示最近访问；每次插入一个新元素时，如果缓存已满，删除链表尾部的元素（即最近最少使用的元素），然后将新元素插入到链表头部。哈希表中存储键值对，其中值为双向链表中的节点，这样可以在 O (1) 时间内找到要操作的节点。

代码实现（Python）：

class ListNode:

def __init__(self, key=0, value=0):

self.key = key

self.value = value

self.prev = None

self.next = None

class LRUCache:

def __init__(self, capacity):

self.capacity = capacity

self.cache = {}

self.head = ListNode()

self.tail = ListNode()

self.head.next = self.tail

self.tail.prev = self.head

def get(self, key):

if key not in self.cache:

return -1

node = self.cache[key]

self._move_to_head(node)

return node.value

def put(self, key, value):

if key in self.cache:

node = self.cache[key]

node.value = value

self._move_to_head(node)

else:

new_node = ListNode(key, value)

self.cache[key] = new_node

self._add_to_head(new_node)

if len(self.cache) > self.capacity:

removed = self._remove_tail()

self.cache.pop(removed.key)

def _move_to_head(self, node):

self._remove_node(node)

self._add_to_head(node)

def _add_to_head(self, node):

node.prev = self.head

node.next = self.head.next

self.head.next.prev = node

self.head.next = node

def _remove_node(self, node):

node.prev.next = node.next

node.next.prev = node.prev

def _remove_tail(self):

node = self.tail.prev

self._remove_node(node)

return node

# 测试

cache = LRUCache(2)

cache.put(1, 1)

cache.put(2, 2)

print(cache.get(1)) # 输出: 1

cache.put(3, 3)

print(cache.get(2)) # 输出: -1

cache.put(4, 4)

print(cache.get(1)) # 输出: -1

print(cache.get(3)) # 输出: 3

print(cache.get(4)) # 输出: 4

代码解释：

ListNode类定义了双向链表的节点结构。

LRUCache类中，__init__方法初始化缓存容量、哈希表和双向链表的头、尾节点。

get方法先检查键是否存在于缓存中，如果存在则将对应的节点移动到链表头部并返回值，否则返回 -1。

put方法如果键已存在，更新值并将节点移动到链表头部；如果键不存在，创建新节点并添加到链表头部，如果缓存已满，删除链表尾部的节点并从哈希表中移除对应的键值对。

_move_to_head、_add_to_head、_remove_node和_remove_tail方法是辅助方法，分别用于将节点移动到链表头部、将节点添加到链表头部、从链表中移除节点和移除链表尾部的节点。

复杂度分析：

时间复杂度：get和put操作的时间复杂度均为 O (1)，因为哈希表的查找和双向链表的插入、删除操作都可以在 O (1) 时间内完成。

空间复杂度：O (capacity)，其中 capacity 是缓存的容量。因为哈希表和双向链表中最多存储 capacity 个元素。

五、总结与建议

DFS 和回溯算法在本质上都依赖递归的思想，DFS 更侧重于对树或图结构的深度遍历，而回溯则是在遍历过程中，通过不断尝试和撤销选择来寻找问题的解，适用于需要穷举所有可能情况的问题。设计类问题则更考验对实际需求的分析和数据结构的运用能力。

对于准备面试的同学，建议多刷相关题型的题目，在刷题过程中，不仅要掌握解题思路和代码实现，还要注重时间复杂度和空间复杂度的分析，不断优化自己的代码。可以使用如 LeetCode、牛客网等在线刷题平台，上面有丰富的题目资源和详细的题解。同时，在面试前，要对常见的面试题进行分类整理，形成自己的解题思路和模板，这样在面试时才能更加从容应对。希望本文能对大家在面试代码高频题的学习和准备中有所帮助，祝大家都能在面试中取得好成绩，拿到心仪的 offer！

面试必知！DFS、回溯、设计代码高频题大揭秘

一、引言

二、DFS 题型

（一）DFS 算法基础

（二）高频面试题讲解 - 岛屿数量

（三）高频面试题讲解 - 岛屿的最大面积

三、回溯题型

（一）回溯算法基础

（二）高频面试题讲解 - 组合

（三）高频面试题讲解 - 复原 IP 地址

四、设计题型

（一）设计类问题特点

（二）高频面试题讲解 - 最小栈

（三）高频面试题讲解 - LRU 缓存机制

五、总结与建议

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签

面试必知！DFS、回溯、设计代码高频题大揭秘

一、引言

二、DFS 题型

（一）DFS 算法基础

（二）高频面试题讲解 - 岛屿数量

（三）高频面试题讲解 - 岛屿的最大面积

三、回溯题型

（一）回溯算法基础

（二）高频面试题讲解 - 组合

（三）高频面试题讲解 - 复原 IP 地址

四、设计题型

（一）设计类问题特点

（二）高频面试题讲解 - 最小栈

（三）高频面试题讲解 - LRU 缓存机制

五、总结与建议

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签