第 94 场周赛：叶子相似的树、模拟行走机器人、爱吃香蕉的珂珂、最长的斐波那契子序列的长度

Q1、叶子相似的树

1、题目描述

请考虑一棵二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

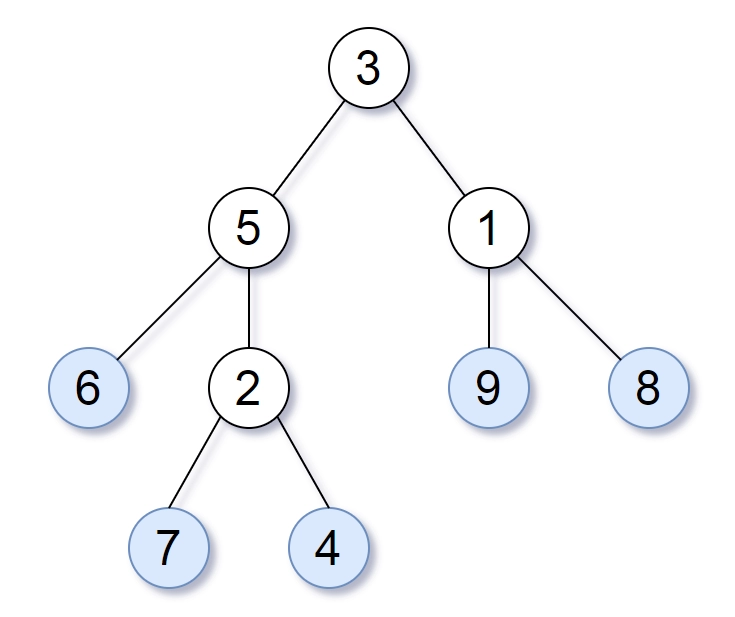
举个例子，如上图所示，给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。

如果有两棵二叉树的叶值序列是相同，那么我们就认为它们是 叶相似 的。

如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

示例 1：

输入：root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]输出：true

示例 2：

输入：root1 = [1,2,3], root2 = [1,3,2]输出：false

提示：

• 给定的两棵树结点数在 [1, 200] 范围内
• 给定的两棵树上的值在 [0, 200] 范围内

2、解题思路

1. DFS遍历：使用深度优先搜索（DFS）遍历两棵二叉树，分别收集它们的叶子节点值。
2. 比较叶值序列：将两棵树的叶值序列存储在数组中，最后比较这两个数组是否完全相同。

3、代码实现

C++

class Solution {public: bool leafSimilar(TreeNode* root1, TreeNode* root2) { vector seq1; // 存储第一棵树的叶值序列 if (root1) { dfs(root1, seq1); // 遍历第一棵树 } vector seq2; // 存储第二棵树的叶值序列 if (root2) { dfs(root2, seq2); // 遍历第二棵树 } // 比较两棵树的叶值序列是否相同 return seq1 == seq2; }private: // 辅助函数: DFS 遍历二叉树, 收集叶子节点值 void dfs(TreeNode* node, vector& seq) { if (!node->left && !node->right) // 如果是叶子节点 { seq.push_back(node->val); // 将叶子结点的值加入序列 } else { // 递归遍历左子树 if (node->left) { dfs(node->left, seq); } // 递归遍历右子树 if (node->right) { dfs(node->right, seq); } } }};

Java

/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */class Solution { // 辅助方法：DFS遍历二叉树，收集叶子节点值 private void dfs(TreeNode node, List<Integer> seq) { if (node.left == null && node.right == null) { // 如果是叶子节点 seq.add(node.val); // 将叶子节点的值加入序列 } else { // 递归遍历左子树 if (node.left != null) { dfs(node.left, seq); } // 递归遍历右子树 if (node.right != null) { dfs(node.right, seq); } } } public boolean leafSimilar(TreeNode root1, TreeNode root2) { List<Integer> seq1 = new ArrayList<>(); // 存储第一棵树的叶值序列 if (root1 != null) { dfs(root1, seq1); // 遍历第一棵树 } List<Integer> seq2 = new ArrayList<>(); // 存储第二棵树的叶值序列 if (root2 != null) { dfs(root2, seq2); // 遍历第二棵树 } // 比较两棵树的叶值序列是否相同 return seq1.equals(seq2); }}

Python

class Solution: def dfs(self, node, seq): if not node.left and not node.right: # 如果是叶子节点 seq.append(node.val)  # 将叶子节点的值加入序列 else: # 递归遍历左子树 if node.left: self.dfs(node.left, seq) # 递归遍历右子树 if node.right: self.dfs(node.right, seq) def leafSimilar(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> bool: seq1 = [] # 存储第一棵树的叶值序列 if root1: self.dfs(root1, seq1) # 遍历第一棵树 seq2 = [] # 存储第二棵树的叶值序列 if root2: self.dfs(root2, seq2) # 遍历第二棵树 # 比较两棵树的叶值序列是否相同 return seq1 == seq2

4、复杂度分析

• 时间复杂度：O(n + m)，其中 n 和 m 分别是两棵树的节点数。需要遍历所有节点。
• 空间复杂度：O(h1 + h2)，其中 h1 和 h2 分别是两棵树的高度。递归栈的深度取决于树的高度。

Q2、模拟行走机器人

1、题目描述

机器人在一个无限大小的 XY 网格平面上行走，从点 (0, 0) 处开始出发，面向北方。该机器人可以接收以下三种类型的命令 commands ：

• -2 ：向左转 90 度
• -1 ：向右转 90 度
• 1 <= x <= 9 ：向前移动 x 个单位长度

在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。

机器人无法走到障碍物上，它将会停留在障碍物的前一个网格方块上，并继续执行下一个命令。

返回机器人距离原点的 最大欧式距离 的 平方 。（即，如果距离为 5 ，则返回 25 ）

注意：

• 北方表示 +Y 方向。
• 东方表示 +X 方向。
• 南方表示 -Y 方向。
• 西方表示 -X 方向。
• 原点 [0,0] 可能会有障碍物。

示例 1：

输入：commands = [4,-1,3], obstacles = []输出：25解释：机器人开始位于 (0, 0)：1. 向北移动 4 个单位，到达 (0, 4)2. 右转3. 向东移动 3 个单位，到达 (3, 4)距离原点最远的是 (3, 4) ，距离为 32 + 42 = 25

示例 2：

输入：commands = [4,-1,4,-2,4], obstacles = [[2,4]]输出：65解释：机器人开始位于 (0, 0)：1. 向北移动 4 个单位，到达 (0, 4)2. 右转3. 向东移动 1 个单位，然后被位于 (2, 4) 的障碍物阻挡，机器人停在 (1, 4)4. 左转5. 向北走 4 个单位，到达 (1, 8)距离原点最远的是 (1, 8) ，距离为 12 + 82 = 65

示例 3：

输入：commands = [6,-1,-1,6], obstacles = []输出：36解释：机器人开始位于 (0, 0):1. 向北移动 6 个单位，到达 (0, 6).2. 右转3. 右转4. 向南移动 6 个单位，到达 (0, 0).机器人距离原点最远的点是 (0, 6)，其距离的平方是 62 = 36 个单位。

提示：

• 1 <= commands.length <= 104
• commands[i] 的值可以取 -2、-1 或者是范围 [1, 9] 内的一个整数。
• 0 <= obstacles.length <= 104
• -3 * 104 <= xi, yi <= 3 * 104
• 答案保证小于 231

2、解题思路

1. 方向管理：机器人初始面向北方，方向可以表示为四个可能的朝向（北、东、南、西）。
2. 障碍物处理：使用哈希集合存储障碍物的位置，便于快速查询。
3. 移动模拟：根据命令逐步移动机器人，遇到障碍物时停止，并记录最大距离。

3、代码实现

C++

class Solution {public: int robotSim(vector& commands, vector<vector>& obstacles) { // 方向数组: 北、东、南、西 (对应前、右、后、左) int dirs[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; int x = 0, y = 0; // 初始位置 int dir = 0; // 初始方向: 北 unordered_set obs; // 存储障碍物 // 将障碍物转换为唯一键存入哈希集合 for (const auto& obstacle : obstacles) { obs.insert(obstacle[0] * 60001 + obstacle[1]); // 避免坐标冲突 } int maxDist = 0; // 记录最大距离的平方 for (int cmd : commands) { if (cmd == -1) // 右转 { dir = (dir + 1) % 4; } else if (cmd == -2) // 左转 { dir = (dir - 1 + 4) % 4; } else // 移动 { for (int step = 0; step < cmd; ++step) {  int nx = x + dirs[dir][0];  int ny = y + dirs[dir][1];  // 检查是否遇到障碍物  if (obs.find(nx * 60001 + ny) != obs.end()) { break;  }  x = nx;  y = ny;  // 更新最大距离  maxDist = max(maxDist, x * x + y * y); } } } return maxDist; }};

Java

class Solution { public int robotSim(int[] commands, int[][] obstacles) { // 方向数组：北、东、南、西 int[][] dirs = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } }; int x = 0, y = 0; // 初始位置 int dir = 0; // 初始方向：北 Set<Integer> obs = new HashSet<>(); // 存储障碍物 // 将障碍物转换为唯一键存入哈希集合 for (int[] obstacle : obstacles) { obs.add(obstacle[0] * 60001 + obstacle[1]); // 避免坐标冲突 } int maxDist = 0; // 记录最大距离的平方 for (int cmd : commands) { if (cmd == -1) { // 右转 dir = (dir + 1) % 4; } else if (cmd == -2) { // 左转 dir = (dir - 1 + 4) % 4; } else { // 移动 for (int step = 0; step < cmd; ++step) {  int nx = x + dirs[dir][0];  int ny = y + dirs[dir][1];  // 检查是否遇到障碍物  if (obs.contains(nx * 60001 + ny)) { break;  }  x = nx;  y = ny;  // 更新最大距离  maxDist = Math.max(maxDist, x * x + y * y); } } } return maxDist; }}

Python

class Solution: def robotSim(self, commands: List[int], obstacles: List[List[int]]) -> int: # 方向列表：北、东、南、西 dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)] x, y = 0, 0 # 初始位置 dir = 0 # 初始方向：北 obs = set() # 存储障碍物 # 将障碍物转换为元组存入集合 for obstacle in obstacles: obs.add((obstacle[0], obstacle[1])) max_dist = 0 # 记录最大距离的平方 for cmd in commands: if cmd == -1: # 右转 dir = (dir + 1) % 4 elif cmd == -2: # 左转 dir = (dir - 1) % 4 else: # 移动 for _ in range(cmd):  nx, ny = x + dirs[dir][0], y + dirs[dir][1]  # 检查是否遇到障碍物  if (nx, ny) in obs: break  x, y = nx, ny  # 更新最大距离  max_dist = max(max_dist, x * x + y * y) return max_dist

4、复杂度分析

• 时间复杂度：O(n + m)，其中 n 是命令的数量，m 是障碍物的数量。
• 空间复杂度：O(m)，用于存储障碍物。

Q3、爱吃香蕉的珂珂

1、题目描述

珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。

珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数）。

示例 1：

输入：piles = [3,6,7,11], h = 8输出：4

示例 2：

输入：piles = [30,11,23,4,20], h = 5输出：30

示例 3：

输入：piles = [30,11,23,4,20], h = 6输出：23

提示：

• 1 <= piles.length <= 104
• piles.length <= h <= 109
• 1 <= piles[i] <= 109

2、解题思路

1. 二分查找：因为 k 的取值范围是在 1 到最大堆的香蕉数之间，所以可以使用二分查找来确定最小的 k。
2. 计算时间：对于每一个候选的 k，计算吃完所有香蕉所需的时间。
3. 调整搜索范围：根据计算的时间调整二分查找的范围，直到找到最小的 k。

3、代码实现

C++

class Solution {private: // 计算以给定速度吃完所有香蕉所需的时间 long getTime(const vector& piles, int speed) { long time = 0; for (int pile : piles) { time += (pile + speed - 1) / speed; // 向上取整 } return time; }public: int minEatingSpeed(vector& piles, int h) { int low = 1;  // 最小速度 int high = *max_element(piles.begin(), piles.end()); // 最大速度 int k = high; // 初始设置为最大速度 while (low < high) { int speed = low + (high - low) / 2; // 中间速度 long time = getTime(piles, speed); // 计算所需时间 if (time <= h) // 如果时间足够, 尝试更小的速度 { k = speed; high = speed; } else // 否则, 增加速度 { low = speed + 1; } } return k; }};

Java

class Solution { public int minEatingSpeed(int[] piles, int h) { int low = 1; int high = Arrays.stream(piles).max().getAsInt(); int k = high; while (low < high) { int speed = low + (high - low) / 2; long time = getTime(piles, speed); if (time <= h) { // 时间足够，尝试更小速度 k = speed; high = speed; } else { // 时间不够，增加速度 low = speed + 1; } } return k; } private long getTime(int[] piles, int speed) { long time = 0; for (int pile : piles) { time += (pile + speed - 1) / speed; // 向上取整 } return time; }}

Python

class Solution: def minEatingSpeed(self, piles: List[int], h: int) -> int: low = 1 high = max(piles) k = high while low < high: speed = (low + high) // 2 time = self.getTime(piles, speed) if time <= h: # 时间足够，尝试更小速度 k = speed high = speed else: # 时间不够，增加速度 low = speed + 1 return k def getTime(self, piles, speed): time = 0 for pile in piles: time += (pile + speed - 1) // speed # 向上取整 return time

4、复杂度分析

• 时间复杂度：O(n log m)，其中 n 是香蕉堆的数量，m 是最大堆的香蕉数。二分查找的时间复杂度是 O(log m)，每次计算时间需要 O(n)。
• 空间复杂度：O(1)，只使用了常数空间。

Q4、最长的斐波那契子序列的长度

1、题目描述

如果序列 x1, x2, ..., xn 满足下列条件，就说它是 斐波那契式 的：

• n >= 3
• 对于所有 i + 2 <= n，都有 xi + xi+1 == xi+2

给定一个 严格递增 的正整数数组形成序列 arr ，找到 arr 中最长的斐波那契式的子序列的长度。如果不存在，返回 0 。

子序列 是通过从另一个序列 arr 中删除任意数量的元素（包括删除 0 个元素）得到的，同时不改变剩余元素顺序。例如，[3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的子序列。

示例 1：

输入: arr = [1,2,3,4,5,6,7,8]输出: 5解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。

示例 2：

输入: arr = [1,3,7,11,12,14,18]输出: 3解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18] 。

提示：

• 3 <= arr.length <= 1000
• 1 <= arr[i] < arr[i + 1] <= 109

2、解题思路

1. 动态规划：使用二维数组 dp 来记录以 arr[i] 和 arr[j] 结尾的斐波那契子序列的长度。
2. 哈希表优化：使用哈希表存储每个元素的索引，以便快速查找是否存在 arr[k] = arr[i] - arr[j]。
3. 状态转移：如果存在 arr[k]，则更新 dp[j][i] 为 dp[k][j] + 1，否则保持默认值。

3、代码实现

C++

class Solution {public: int lenLongestFibSubseq(vector& arr) { unordered_map indices; // 存储元素到索引的映射 int n = arr.size(); for (int i = 0; i < n; ++i) { indices[arr[i]] = i; // 记录每个元素的索引 } vector<vector> dp(n, vector(n, 0)); // dp[i][j] 表示以 arr[i] 和 arr[j] 结尾的斐波那契子序列的长度 int ans = 0;  // 记录最大长度 for (int i = 0; i = 0 && arr[j] * 2 > arr[i];  --j) // 确保 arr[k] < arr[j] < arr[i] { int k_val = arr[i] - arr[j]; // 计算 arr[k] 的值 if (indices.count(k_val)) // 如果存在 arr[k] {  int k = indices[k_val]; // 获取 arr[k] 的索引  dp[j][i] = max(dp[k][j] + 1, 3); // 更新 dp[j][i] } ans = max(ans, dp[j][i]); // 更新最大长度 } } return ans; }};

Java

class Solution { public int lenLongestFibSubseq(int[] arr) { Map<Integer, Integer> indices = new HashMap<>(); // 存储元素到索引的映射 int n = arr.length; for (int i = 0; i < n; i++) { indices.put(arr[i], i); // 记录每个元素的索引 } int[][] dp = new int[n][n]; // dp[i][j] 表示以 arr[i] 和 arr[j] 结尾的斐波那契子序列的长度 int ans = 0; // 记录最大长度 for (int i = 0; i < n; i++) { for (int j = i - 1; j >= 0 && arr[j] * 2 > arr[i]; j--) { // 确保 arr[k] < arr[j] < arr[i] int k_val = arr[i] - arr[j]; // 计算 arr[k] 的值 if (indices.containsKey(k_val)) { // 如果存在 arr[k]  int k = indices.get(k_val); // 获取 arr[k] 的索引  dp[j][i] = Math.max(dp[k][j] + 1, 3); // 更新 dp[j][i] } ans = Math.max(ans, dp[j][i]); // 更新最大长度 } } return ans; }}

Python

class Solution: def lenLongestFibSubseq(self, arr: List[int]) -> int: indices = {num: i for i, num in enumerate(arr)} # 存储元素到索引的映射 n = len(arr) dp = [[0] * n for _ in range(n)] # dp[i][j] 表示以 arr[i] 和 arr[j] 结尾的斐波那契子序列的长度 ans = 0 # 记录最大长度 for i in range(n): j = i - 1 while j >= 0 and arr[j] * 2 > arr[i]: # 确保 arr[k] < arr[j] < arr[i] k_val = arr[i] - arr[j] # 计算 arr[k] 的值 if k_val in indices: # 如果存在 arr[k]  k = indices[k_val] # 获取 arr[k] 的索引  dp[j][i] = max(dp[k][j] + 1, 3) # 更新 dp[j][i] ans = max(ans, dp[j][i]) # 更新最大长度 j -= 1 return ans

4、复杂度分析

• 时间复杂度：O(n^2)，其中 n 是数组的长度。需要双重循环遍历数组。
• 空间复杂度：O(n^2)，用于存储动态规划表。