NOIP学习笔记——动态规划dp基础

目录

一.定义

二.条件

三.要点

四.例题

（一）最值问题

1.hdu1260 门票

2.洛谷P1216 数字三角形

3.POJ 3278 Catch that cow

（二）方案数

1.P1192台阶问题

2.三扔硬币

（三）推状态

1.放苹果

2.吃糖果

---

一.定义

简单来讲，动态规划就是将一个大问题拆分成几个小问题，以小问题的解推向大问题答案的过程。

二.条件

动态规划需要满足两个条件：

1.最优子结构：即小问题的最优解必推向大问题的最优解

2.无后效性：把状态看成图上的一个点，转移看成图上的一条边，最后整张状态图一定要是一个 有向无环图 ，才是无后效性的。

举个例子：

经典斐波那契数列的递推公式为：，即第i个数为前两个数之和，

将它变成图是这样的：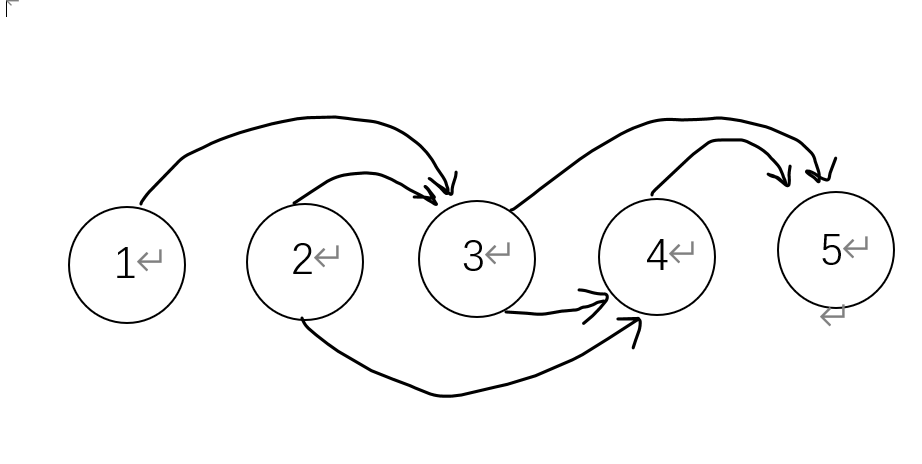

但若递推式为,它的图是这样的：

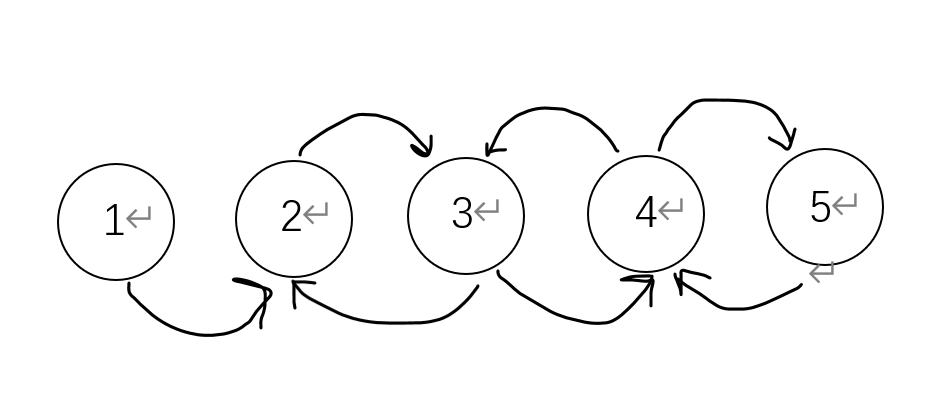
很明显全是环，那么它就不满足无后效性这一特点。

三.要点

破解一个动态规划问题，一定要明确五要素：状态、转移方程、初始化、枚举顺序以及答案表示。

例如斐波那契数列：

状态：f[i]表示第 i项的斐波那契数列值。

转移方程：f[i]=f[i−1]+f[i−2]

初始化：f[1]=f[2]=1

枚举顺序：3→n

答案表示：dp[n]

将这五个全列出来，问题就完成一大半了。

四.例题

dp题目按目的分一共有两大类：求最值与求方案数。

（一）最值问题

1.hdu1260 门票

题目大意：Joe正在卖票，每一次他可以选择卖给一个人票或者卖给两个相邻的人票，问他卖完票所需的最短时间。

题目分析：

状态：f[i]表示前i个人买票最优解
方程：考虑达到当前状态的最后一步（第i个人买票：和前一个人一起买/自己买）
          
初始化：
顺序：3->n
答案表示：f[n]

 再注意一下答案的格式，AC代码就出来了。

2.洛谷P1216 数字三角形

题目分析：

这里从一维的问题升级到二维的问题，一层一层往下走时，前面选什么数都无所谓，重要的只有走到某个点时的最大值，因此可以得出：

状态：f[i][j]表示走到(i,j)时的最大和

方程：

走到（i，j）的上一步为（i-1,j)或(i-1,j-1)，从这两个地方进行转移。

初始化：

顺序：r\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?i%3A2-%3Er\" />

          i\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?j%3A1-%3Ei\" />

答案：

3.POJ 3278 Catch that cow

状态：f[i]表示走到i点的最小时间

方程：

初始化：往后走只能一步一步走。

for(int i=0;i<=n;i++) f[i]=n-i;

答案：f[k]

那么这里很明显有一个问题：根据转移方程，我要在求f[i]之前同时知道f[i-1]和f[i+1]的值，根据前面关于后效性的分析，这很明显不属于无后效性的特征。

因此我们需要去除后效性。

去除后效性的方法：

1.移项

如

可将其移项后变为：

再转化一下：

这个式子就变得无后效性了。

2.多走几步，等效替换

也是本问题用的方法。

假如我们需要从3走到5，可以一步一步走过去，共走2步。

那么我们为什么不从3飞到6，再退回一步呢？不难发现，它们两个步数是等效的。

由此可见，对于k为偶数来说，

f[i]=min(f[i-1]+1,f[i/2]+1);

而对于k为奇数来说，

f[i]=min(f[(i-1)/2]+2,f[(i+1)/2]+2);//(i-1)/2->i-1->i或(i+1)/2->i+1->i

我们将其变为两步一走来看，以消除它的后效性。

但这个代码还有一个问题。

当我们要从12走到13时，上面的代码必走两步及以上，但实际上，我们只需要一步就够了。

所以我们将这种情况也考虑进去，最后的核心代码如下：

for(int i=n+1;i<=k;i++){ f[i]=f[i-1]+1; if(i%2==0){ f[i]=min(f[i],f[i/2]+1); } else f[i]=min({f[i-1]+1,f[(i-1)/2]+2,f[(i+1)/2]+2}); }

（二）方案数

1.P1192台阶问题

模板题

状态：f[i]表示走到第i级台阶的方案数
转移：for(int j=1;j<=min(k,i);j++) f[i]+=f[i-j];
初始化：f[0]=1
顺序：i:1->n

           j:1->min(k,i)
答案：f[n]

2.三扔硬币

题目描述：

扔n次硬币的结果可以用一串0/1序列来表示。给定n，请统计有多少种扔硬币的结果中不含三个连续的0且不含三个连续的1。

当n较大的时候，答案可能很大，所以输出答案模1,000,000,007的余数即可。

在看这道题之前，我们先来看一道简单一点的题：

长度为N的01字符串，且满足串中不能有两个或多个连续的0的方案数有多少种？

例如，10、10101、11101是满足条件的，而00、10001、10010是不满足条件的。

题目分析：

对于第i个数来说，对它有影响的只有前一个数的取值，我们可以加一维来记录这次的数为0还是1，如果是1就没有影响，前一个位置可以是1或0。如果是0，前一个位置只能是1.

状态：f[i][j]表示前i位数字且第i位结果为0或1的方案数(j=0/1)
方程：
          
初始化：
顺序：2->n
答案：

回到三扔硬币这道题，两道题的区别，只是从控制前一位变成了控制前两位而已。

所以可以在状态上再加一维，控制第i-1次结果为0或1。

状态：f[i][j][k]扔第i次硬币且第i次结果为j且前一次为k的方案数
方程：(f[i][0][0]相同)
           (f[i][0][1]相同)
初始化：
顺序：2->n
答案：sum(f[n][j][k])

完整代码：

#includeusing namespace std;int mod=1000000007;int f[1000005][2][2];int main(){ int n; cin>>n; if(n==1) {//特判 cout<<2<<endl; return 0; } f[2][1][1]=f[2][0][1]=f[2][0][0]=f[2][1][0]=1; for(int i=3;i<=n;i++){ f[i][1][1]=f[i-1][1][0]%mod; f[i][0][0]=f[i-1][0][1]%mod; f[i][1][0]=(f[i-1][0][1]+f[i-1][0][0])%mod; f[i][0][1]=(f[i-1][1][0]+f[i-1][1][1])%mod; } cout<<((f[n][1][1]+f[n][0][0])%mod+(f[n][1][0]+f[n][0][1])%mod)%mod;//记得取模 return 0;}

以上无论是求最值还是方案数，都是状态的难度>方程的难度，接下来两道题个人认为方程难度>状态难度。

（三）推状态

1.放苹果

题目描述：把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？（用K表示）5，1，1和1，5，1 是同一种分法。

题目分析：

状态：f[i][j]表示前i个盘子共放j个苹果。

转移方程：看到这道题，很容易想到数学中隔板法的经典排列组合做法，但是由于几个盘子是相同的，去重比较麻烦。

因此，我们要想一个办法，使dp中的方案数不重复。

从枚举的角度来考虑，只要我们保证a[1]>=a[2]>=……>=a[n]，那我们的方案一定是不重复的。

那么如何做到这一点呢？

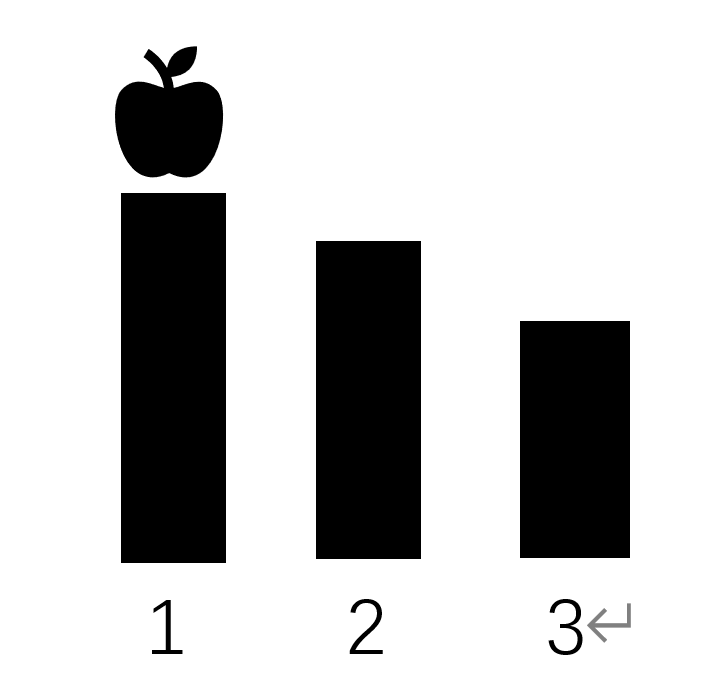
假如我已经有了一个降序序列，我在一号位添加苹果，它们依旧保持降序排列。

   但如果我在二号位添加，那就不一定为降序排列了。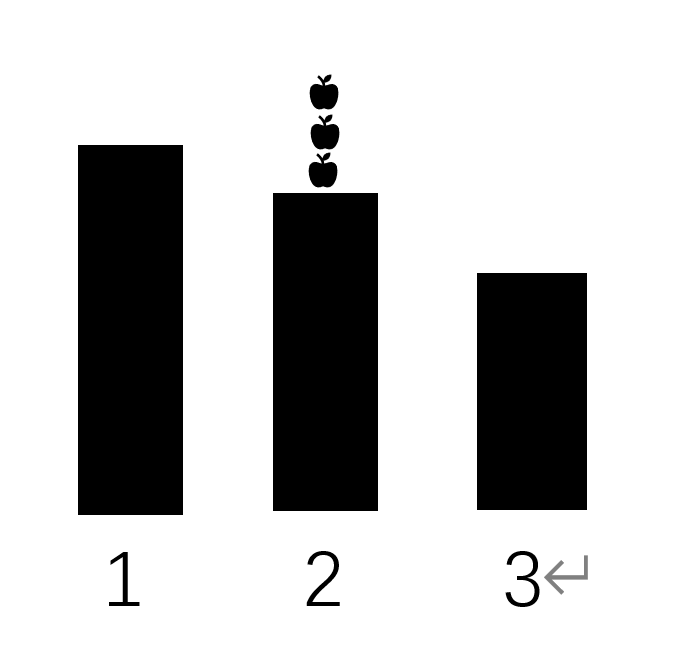

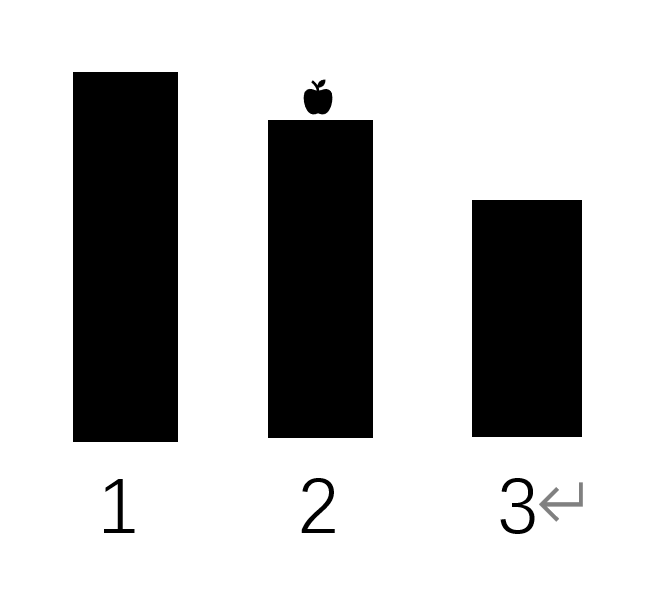
假如我要保持它们的降序差值，我们可以使用一个办法：给这i个位置一起加同样个数的苹果，这样它们的相对差值不变。

那么我们如何获得不同差值的结果呢？可以添加1个空盘子，就可以保证所有可能的差值都会被计算到。

得出方程：

//控制一下不要越界if(j>=i) f[i][j]=f[i-1][j]+f[i][j-i];else f[i][j]=f[i-1][j];

 完整代码：

#includeusing namespace std;int f[20][20];//状态int main(){ f[0][0]=1;//初始化 for(int i=1;i<=10;i++){ for(int j=0;j=i) f[i][j]=f[i-1][j]+f[i][j-i];//方程 else f[i][j]=f[i-1][j]; } } int t; cin>>t; while(t--){//本道题是多组数据，在前面提前把所有数据处理好 int m,n; cin>>m>>n; cout<<f[n][m]<<endl; } return 0;}

2.吃糖果

题目描述：

Yui有n个糖果，她一天最多吃m个糖果。

第i个糖果的甜度值初始值为ai​，第d天会变成d∗ai。

问吃k（1≤k≤n）个糖果的最小甜度和值分别是多少。

输入样例：

9 26 19 3 4 4 2 6 7 8

输出样例：

2 5 11 18 30 43 62 83 121

题目分析：

状态：吃k个糖果的最小甜度和

方程：

1.假如Yui没有吃完全部的糖果，那么她一定吃甜度较小的糖果。

2.在Yui吃的糖果中，甜度小的一定后吃。

样例分析：

1.排序：2 3 4 4 6 6 7 8 19

2.吃一个糖：2           f[1]=2

   吃两个糖：3 2        f[2]=2+3

   吃三个糖：4 3 | 2   f[3]=4+3+2+2=f[1]+sum[3]

   吃四个糖：4 4 | 3 2 f[4]=4+4+3+2+3+2=f[2]+sum[4]

总结：m)\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?f%5Bi%5D%3Df%5Bi-m%5D&plus;sum%5Bi%5D%28i%3Em%29\" />

画图分析：

我们可以将吃糖视作平推的过程,由于天数的变化，甜度会有差值。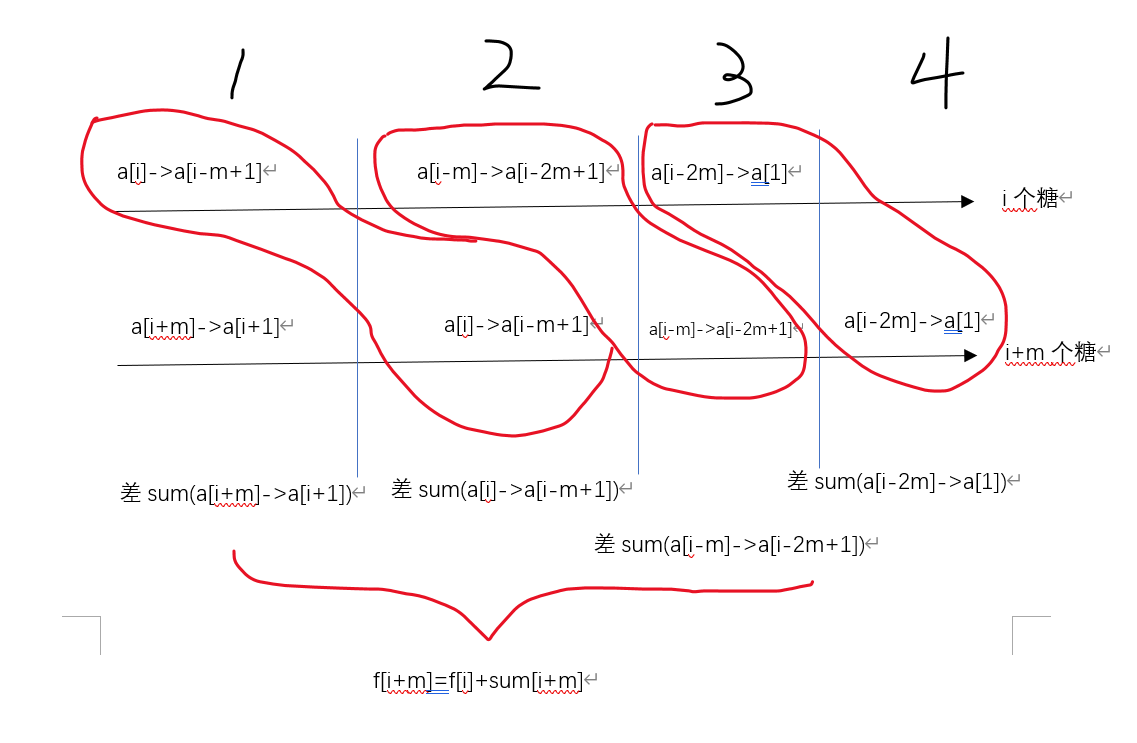

 由此可得方程：m)\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?f%5Bi%5D%3Df%5Bi-m%5D&plus;sum%5Bi%5D%28i%3Em%29\" />

完整代码：

/*9 22 3 4 4 6 6 7 8 19- f[1]=a[1] 2-- f[2]=a[1]+a[2] 5--|- f[3]=a[1]+a[2]+a[3]+a[1]--|-- =f[1]+f[2]+a[3] f[4]=a[1]+a[2]+a[3]+a[4]+a[2]+a[1]=f[2]+sum[4]--|--|- f[5]=a[1]+a[2]+a[3]+a[4]+a[5]+a[1]+a[2]+a[3]+a[1]=f[3]+sum[5]f[i]=f[i-m]+sum[i];*/#includeusing namespace std;long long a[200005],sum[200005],f[200005];int main(){ int n,m; cin>>n>>m; for(int i=1;i>a[i]; sort(a+1,a+1+n); for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i]; for(int i=1;i<=m;i++) f[i]=f[i-1]+a[i]; for(int i=m+1;i<=n;i++) f[i]=f[i-m]+sum[i]; for(int i=1;i<=n;i++) cout<<f[i]<<\" \"; return 0;}