【图论】最短路算法

知识点图片来源于董晓算法

图的存储：链式前向星

const int N=1e3+10,M=2e3+10,mod=998244353,inf=0x3f3f3f3f;//1e5就超时struct edge{ int to,w,nxt;};edge e[N];//实际存储容器int head[N],tot;int n,m;void init(){ forr(i,0,M)e[i].nxt=0; forr(i,0,N)head[i]=0; tot=0;}void addedge(int u,int v,int w){//加点 e[++tot].to=v;//指向的点 e[tot].w=w; e[tot].nxt=head[u]; head[u]=tot;}void solve(){ cin>>n>>m; forr(i,1,m){ int u,v,w;cin>>u>>v>>w; addedge(u,v,w); } //遍历一个点的出边 int now=3; for(int i=head[now];i;i=e[i].nxt){ cout<<e[i].to<<\' \'<<e[i].w<<endl; }}

单源最短路

Dijkstra

O(n2)模板

样例
输入
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出
0 2 4 3

const int N=1e4+10,mod=998244353,inf=pow(2,31)-1;//1e5就超时struct edge{ int v,w;};int n,m,st;vector<edge>e[N];int dis[N],vis[N];void dij(int s){ forr(i,0,n)dis[i]=inf;//都初始化为inf 注意now初始为0 dis[0]=inf dis[s]=0; forr(i,1,n){ int now=0; forr(j,1,n)//取出距离st最短的点 if(!vis[j]&&dis[j]<dis[now])now=j; vis[now]=1;//拿出来 // cout<<now<<endl; for(auto ed:e[now]){//用now做跳板更新相邻的边 int v=ed.v,w=ed.w; if(dis[v]>dis[now]+w)dis[v]=dis[now]+w; } }}void solve(){ cin>>n>>m>>st; forr(i,1,m){ int a,b,val; cin>>a>>b>>val; e[a].push_back({b,val}); } dij(st); forr(i,1,n)cout<<dis[i]<<\' \';}

只适用于正边权，不能用于负边权
O(n2)
n=1e3 m=1e6稠密图能过
n=1e6 m=1e6 T

O(mlogm)堆优化

const int N=1e5+10,mod=998244353,inf=pow(2,31)-1;//1e5就超时struct edge{ int v,w;};int n,m,st;vector<edge>e[N];int dis[N],vis[N];priority_queue<pair<int,int>>q;//默认为大根堆void dij(int s){ forr(i,0,n)dis[i]=inf;//都初始化为inf 注意now初始为0 dis[0]=inf dis[s]=0;q.push(make_pair(0,s)); while (q.size()) { auto t=q.top();q.pop(); int now=t.second; if(vis[now])continue;//把之前插入优先队列的遍历过的点跳过 vis[now]=1; for(auto ed:e[now]){//用now做跳板更新相邻的边 松弛操作 int v=ed.v,w=ed.w; if(dis[v]>dis[now]+w){ dis[v]=dis[now]+w; q.push(make_pair(-dis[v],v));//把更新过的点扔进堆里 d[v]越小 -d[v]越大 利用负号构建小根堆 } } }}void solve(){ cin>>n>>m>>st; forr(i,1,m){ int a,b,val; cin>>a>>b>>val; e[a].push_back({b,val}); } dij(st); forr(i,1,n)cout<<dis[i]<<\' \';}

O(mlogm)
m=1e6可过

路径记录和输出

void dij(int s){ forr(i,0,n)dis[i]=inf;//都初始化为inf 注意now初始为0 dis[0]=inf dis[s]=0;q.push(make_pair(0,s)); while (q.size()) { auto t=q.top();q.pop(); int now=t.second; if(vis[now])continue;//把之前插入优先队列的遍历过的点跳过 vis[now]=1; for(auto ed:e[now]){//用now做跳板更新相邻的边 松弛操作 int v=ed.v,w=ed.w; if(dis[v]>dis[now]+w){ dis[v]=dis[now]+w; pre[v]=now;//记录前驱点 q.push(make_pair(-dis[v],v));//把更新过的点扔进堆里 d[v]越小 -d[v]越大 利用负号构建小根堆 } } }}//输出任意一点到st的最短路径void dfs_path(int now){//dfs从末点遍历到st if(now==st)return cout<<now<<endl,void(); dfs_path(pre[now]); cout<<now<<endl;}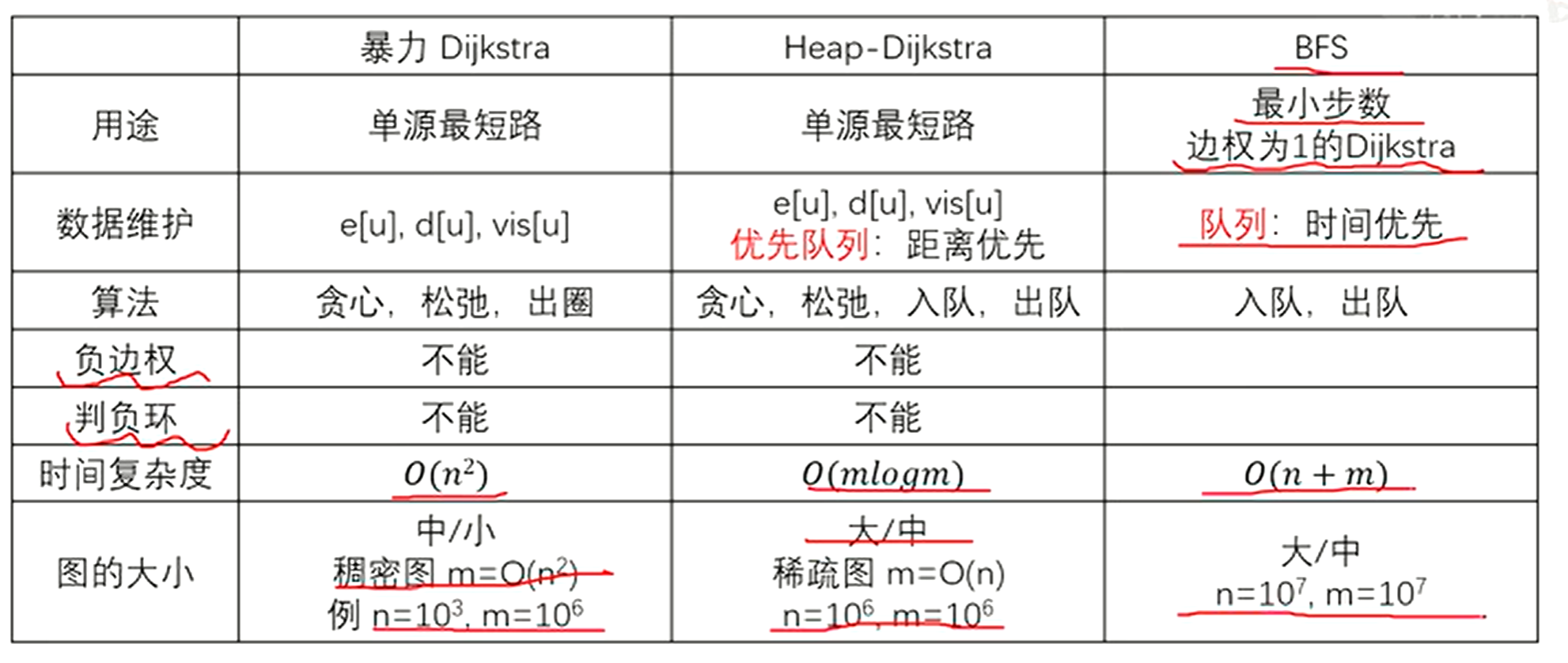

Bellman-Ford O(nm)

可以用来判断负环
P3385

struct edge{int v,w;};vector<edge>e[N];int d[N];//距离int n,m;bool bellmanford(int s){ forr(i,1,n)d[i]=inf; d[s]=0; bool fg;//是否松弛 //O(nm) forr(i,1,n){//更新n次 因为一个点可以多次更新，所以可判负环 fg=0; forr(u,1,n){//以每一个点为跳板 if(d[u]==inf)continue; for(auto ed:e[u]){//更新每条出边 int v=ed.v,w=ed.w; if(d[v]>d[u]+w)d[v]=d[u]+w,fg=1; } } if(!fg)break; } return fg;//第n轮仍为true则有环 因为负边权让d越来越小 必定有松弛操作}void solve(){ cin>>n>>m; forr(i,1,n)e[i].clear(); forr(i,1,m){ int u,v,w;cin>>u>>v>>w; e[u].push_back({v,w}); if(w>=0)e[v].push_back({u,w}); } cout<<(bellmanford(1)?\"YES\":\"NO\")<<endl;}

SPFA O(nm) queue维护

struct edge{int v,w;};vector<edge>e[N];int d[N],vis[N],cnt[N],pre[N];//距离int n,m;//O(nm)bool spfa(int s){ memset(d,0x3f,sizeof d); memset(cnt,0,sizeof cnt); memset(vis,0,sizeof vis); memset(pre,0,sizeof pre); queue<int>q; d[s]=0,vis[s]=1; q.push(s); while(q.size()){ int now=q.front();q.pop(); vis[now]=0;//出队 可反复进队出队 for(auto ed:e[now]){ int v=ed.v,w=ed.w; if(d[v]>d[now]+w){ d[v]=d[now]+w; cnt[v]=cnt[now]+1; pre[v]=now;//记录前驱点 if(cnt[v]>=n)return true;//这条路上边数有重复点 就有负边 if(!vis[v])q.push(v),vis[v]=1;//v不在队内 就放进去 } } } return false;}void dfs_path(int now,int s){ if(now==s){//递归到起点 cout<<now<<endl; return; } dfs_path(pre[now],s); cout<<now<<endl;}void solve(){ cin>>n>>m; forr(i,1,n)e[i].clear(); forr(i,1,m){ int u,v,w;cin>>u>>v>>w; e[u].push_back({v,w}); if(w>=0)e[v].push_back({u,w}); } cout<<(spfa(1)?\"YES\":\"NO\")<<endl;}

多源最短路

Floyd 动态规划思想 O(n3)

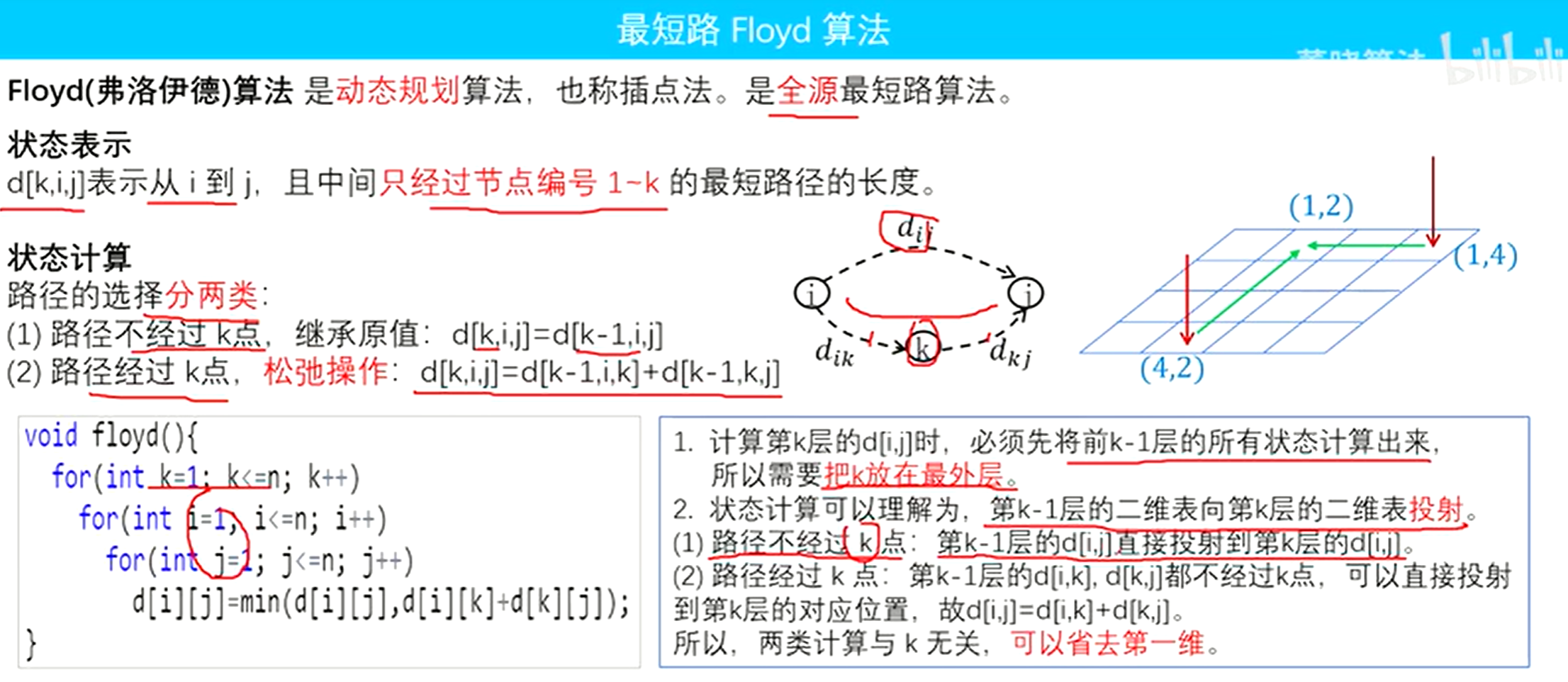
使用邻接矩阵

“插点”的思想

路径输出

Johnson 虚拟原点0 O(nmlogm)

一次SPFA，n次HD

P5905

const int N=3e3+10,M=6e3+10,mod=998244353,inf=1e9;struct edge{int v,w;};vector<edge>e[N];int h[N],d[N],vis[N],cnt[N];int n,m;void spfa(int s){ forr(i,0,n)h[i]=inf; memset(cnt,0,sizeof cnt); memset(vis,0,sizeof vis); queue<int>q; h[s]=0,vis[s]=1; q.push(s); while(q.size()){ int now=q.front();q.pop(); vis[now]=0;//出队 可反复进队出队 for(auto ed:e[now]){ int v=ed.v,w=ed.w; if(h[v]>h[now]+w){ h[v]=h[now]+w; cnt[v]=cnt[now]+1; if(cnt[v]>n){  cout<<\"-1\\n\";  exit(0); } if(!vis[v])q.push(v),vis[v]=1;//v不在队内 就放进去 } } }}void dij(int s){ forr(i,0,n)d[i]=inf;//都初始化为inf 注意now初始为0 d[0]=inf memset(vis,0,sizeof vis); priority_queue<pair<int,int>>q; d[s]=0;q.push(make_pair(0,s)); while (q.size()) { auto t=q.top();q.pop(); int now=t.second; if(vis[now])continue;//把之前插入优先队列的遍历过的点跳过 vis[now]=1; for(auto ed:e[now]){//用now做跳板更新相邻的边 松弛操作 int v=ed.v,w=ed.w; if(d[v]>d[now]+w){ d[v]=d[now]+w; q.push(make_pair(-d[v],v));//把更新过的点扔进堆里 d[v]越小 -d[v]越大 利用负号构建小根堆 } } }}void solve(){ cin>>n>>m; forr(i,1,m){ int u,v,w;cin>>u>>v>>w; e[u].push_back({v,w}); } forr(i,1,n){ e[0].push_back({i,0}); } spfa(0);//h[i]是0到i点的最短路 forr(i,1,n){ for(auto &ed:e[i]){ ed.w+=h[i]-h[ed.v];//修改边权 加头去尾 } } forr(i,1,n){ dij(i);//以每个点为源跑dij d[j]是i到j的最短路 int ans=0; forr(j,1,n){ if(d[j]==inf)ans+=j*inf; else ans+=j*(d[j]+h[j]-h[i]);//还原权值 } cout<<ans<<endl; }}

总结