网站导航
> 技术文档 > 数据结构之探索“栈”的奥秘

数据结构之探索“栈”的奥秘

网友: 技术文档 2025-09-03 12:00:58

找往期文章包括但不限于本期文章中不懂的知识点：

个人主页：我要学编程(ಥ_ಥ)-CSDN博客

所属专栏：数据结构（Java版）

目录

栈的有关概念

栈的使用 

栈的模拟实现

栈的应用场景

改变元素的序列

将递归转化为循环 

栈的相关刷题 

20. 有效的括号

150. 逆波兰表达式求值

牛客网——JZ31 栈的压入、弹出序列

155. 最小栈

栈的有关概念

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

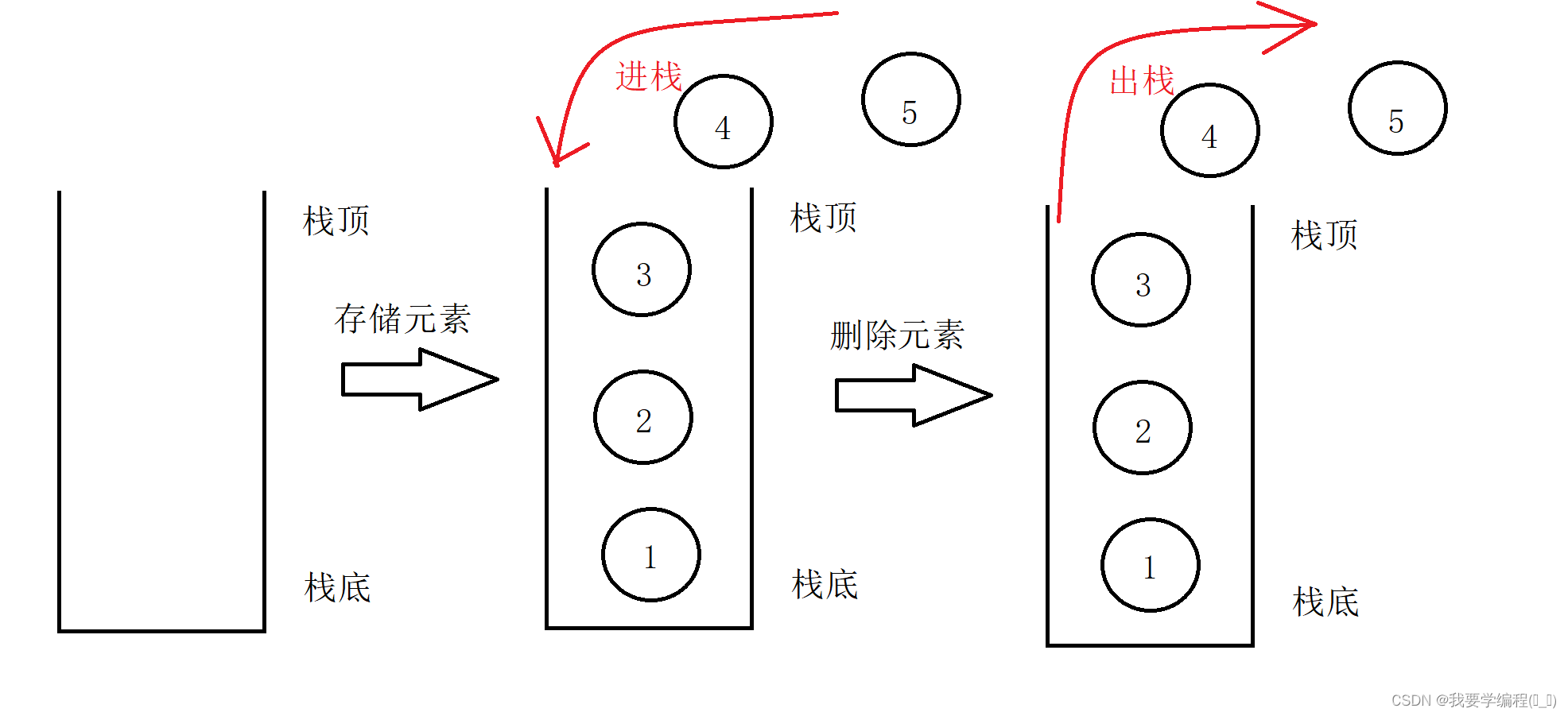
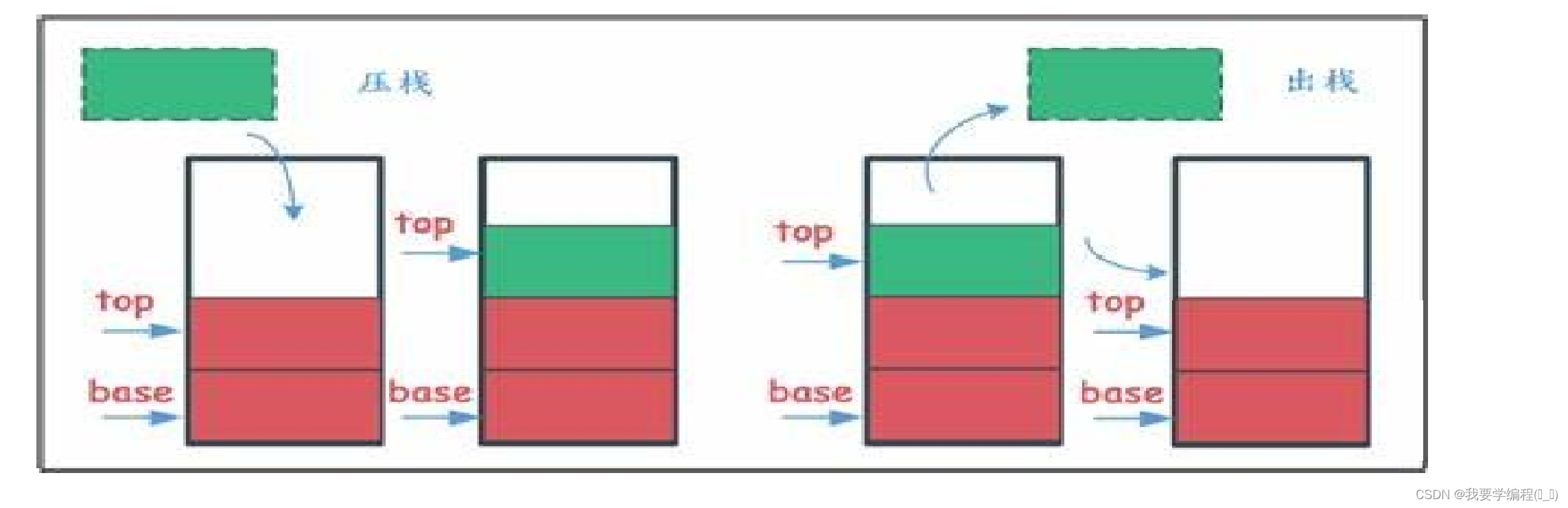
压栈：栈的插入操作叫做进栈/压栈/入栈。 出栈：栈的删除操作叫做出栈。

下面是栈以及其有关操作的图示：

栈的使用 

栈的基本方法 方法 功能 Stack() 构造一个空的栈 E push(E e) 将e入栈，并返回e E pop() 得到并删除栈顶元素 E peek() 获取栈顶元素 int size() 获取栈中有效元素的个数 boolean empty() 检测栈是否为空

下面是上面方法的使用：

public class Test { public static void main(String[] args) { // 构造方法：构造一个空栈 Stack stack = new Stack(); // 判断栈是否为空 System.out.println(stack.empty()); // 开始往栈区增加元素：压栈/入栈 stack.push(1); stack.push(2); stack.push(3); stack.push(4); stack.push(5); // 获取栈顶元素 System.out.println(stack.peek()); // 得到并删除栈顶元素 System.out.println(stack.pop()); // 获取栈中有效的元素个数 int size = stack.size(); System.out.println(size); // 开始利用pop方法遍历栈 for (int i = 0; i < size; i++) { // 得到并删除栈顶元素 System.out.println(stack.pop()); } // 判断栈是否为空 System.out.println(stack.empty()); }}

运行结果：

栈的模拟实现

模拟栈，就只需要实现模拟我们上面使用的那几种方法即可。

下面是用数组模拟栈的实现：

// 用数组模拟实现栈public class MyStack { public int[] elem; public int usedSzie; public MyStack() { // 为了方便测试给三个空间 this.elem = new int[3]; } // 入栈 public boolean push(int val) { // 先判断栈空间是否满了 if (this.usedSzie == this.elem.length) {  return false; } this.elem[(this.usedSzie)++] = val; return true; } // 出栈 public int pop() throws StackIsEmptyException { // 先判断栈是否为空 if (empty()) {  throw new StackIsEmptyException(\"栈为空异常!\"); } else { this.usedSzie--; return this.elem[this.usedSzie]; } } // 获取栈顶元素 public int peek() { // 先判断栈是否为空 if (empty()) {  throw new StackIsEmptyException(\"栈为空异常!\"); } else {  return this.elem[this.usedSzie-1]; } } public int size() { return this.usedSzie; } public boolean empty() { return this.usedSzie == 0; }}

异常代码：

public class MyStackIsEmptyException extends RuntimeException { public MyStackIsEmptyException(String msg) { super(msg); } public MyStackIsEmptyException() { super(); }}

除了用数组之外，还可以用链表来模拟实现：

// 用链表来模拟实现栈public class MyStack { public LinkedList linkedList; public MyStack () { this.linkedList = new LinkedList(); } // 入栈 public void push(int val) { // 直接尾插就行 this.linkedList.addLast(val); } // 出栈 public int pop() throws MyStackIsEmptyException { // 先判断链表是否为空 if (empty()) { throw new MyStackIsEmptyException(\"栈为空异常！\"); } // 移除最后一个节点 int ret = this.linkedList.getLast(); // 得到最后一个元素 this.linkedList.removeLast(); return ret; } // 获取栈顶元素 public int peek() throws MyStackIsEmptyException { // 先判断链表是否为空 if (empty()) { throw new MyStackIsEmptyException(\"栈为空异常！\"); } return this.linkedList.getLast(); } public int size() { return this.linkedList.size(); } public boolean empty() { return this.linkedList.size() == 0; }}

当然，这里的链表没有自己实现，而是用的Java自身提供的。那么也意味着上面的数组实现，可以用顺序表来模拟，也是一样的。 

栈的应用场景

改变元素的序列

例1： 

我们知道栈要遵循一个规律：先进后出，后进先出。那么只要 先进去的 在 后进去的 前面出来，则肯定是错误的。

A选项，正确。当1进去栈，接着再出来，后面的接着全部进去，再一个一个的出来，那么结果就是 1、4、3、2。

B选项，正确。1进去，接着2进去，再出来，一直循环这个过程到全部元素进去，最后1再出来，那么结果就是2、3、4、1。 

C选项，错误。3 要出来，说明1 和 2肯定已经进去了。既然3出去了，栈中就只有1和2了，并且2在栈顶，那么就不可能出现1 比 2先出去的情况。

D选项，正确。3 要出来，肯定 1 和 2 进去了。接着 4再进去、出来。最后就是2 出来，1出来。那么结果就是3、4、2、1。

例2：

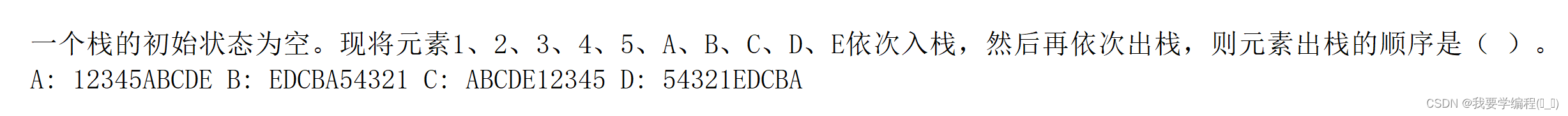
这个答案就很明显了是B。

将递归转化为循环 

例如：逆序打印单链表。

正常打印单链表是从头节点开始一直遍历到 null 就停下。但是现在要逆序打印，就是从尾节点开始打印这个单链表。

方式一，递归：

 // 逆序打印节点的值 public void printList(ListNode head) { //if (head == null) { // // 抛异常 //} // 找到尾节点就停止 if (head.next != null) { printList(head.next); } System.out.print(head.val+\" \"); }

方式二，栈：

要逆序打印单链表，就是从尾节点开始打印，而尾节点是后面进来的。即后面来的先打印，前面的后打印。这个就可以用栈来实现。

 public void printList(ListNode head) { /*if (head == null) { // 抛异常 }*/ // 创建一个栈 Stack stack = new Stack(); // 遍历链表，把链表的节点放到栈中 while (head != null) { stack.push(head.val); head = head.next; } // 开始用栈来打印 while (!stack.empty()) { System.out.print(stack.pop()+\" \"); } }

栈的相关刷题 

20. 有效的括号

给定一个只包括 \'(\'，\')\'，\'{\'，\'}\'，\'[\'，\']\' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。
  3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = \"()\"输出：true

示例 2：

输入：s = \"()[]{}\"输出：true

示例 3：

输入：s = \"(]\"输出：false

提示：

  • 1 <= s.length <= 104
  • s 仅由括号 \'()[]{}\' 组成

括号不匹配有三种情况：

1、左括号比右括号多

2、右括号比左括号多

3、左右括号不匹配 

当我们去遍历这个字符串时，会发现一个规律：后遇到的左括号 会比 前遇到的左括号 先匹配。

思路： 先遇到的左括号储存到栈中，直至遇到了右括号，再将栈顶元素拿出来和这个右括号进行匹配，看看是否成功。 成功就继续往后走，失败则返回false。直至遍历完成或者栈为空（右括号多于左括号）。

class Solution { public boolean isValid(String s) { // 创建一个栈 Stack stack = new Stack(); // 遍历字符串 for (int i = 0; i < s.length(); i++) { char ch = s.charAt(i); // 如果遇到左括号就入栈，如果遇到右括号就出栈 if (ch == \'(\' || ch == \'{\' || ch == \'[\') { stack.push(ch); }else { // 出栈匹配 // 判断栈是否为空 if (stack.empty()) {  return false; } else {  // 开始匹配  char x = stack.pop();  // 如果匹配说明符合要求，继续往后走  if (x == \'(\' && ch == \')\') { continue;  } else if (x == \'[\' && ch == \']\') { continue;  } else if (x == \'{\' && ch == \'}\') { continue;  } else { return false;  }  } } } // 判断栈是否为空 if (stack.empty()) { // 栈为空说明全部匹配成功了 return true; } else { // 还有括号没有匹配 return false; } }}

150. 逆波兰表达式求值

逆波兰表达式的介绍

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

  • 有效的算符为 \'+\'、\'-\'、\'*\' 和 \'/\' 。
  • 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
  • 两个整数之间的除法总是 向零截断 。
  • 表达式中不含除零运算。
  • 输入是一个根据逆波兰表示法表示的算术表达式。
  • 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = [\"2\",\"1\",\"+\",\"3\",\"*\"]输出：9解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = [\"4\",\"13\",\"5\",\"/\",\"+\"]输出：6解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = [\"10\",\"6\",\"9\",\"3\",\"+\",\"-11\",\"*\",\"/\",\"*\",\"17\",\"+\",\"5\",\"+\"]输出：22解释：该算式转化为常见的中缀算术表达式为： ((10 * (6 / ((9 + 3) * -11))) + 17) + 5= ((10 * (6 / (12 * -11))) + 17) + 5= ((10 * (6 / -132)) + 17) + 5= ((10 * 0) + 17) + 5= (0 + 17) + 5= 17 + 5= 22

提示：

  • 1 <= tokens.length <= 104
  • tokens[i] 是一个算符（\"+\"、\"-\"、\"*\" 或 \"/\"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式（也称为后缀表达式）的计算通常与栈密切相关，因为栈能够非常自然地处理这种后进先出的操作顺序。不过，理论上讲，不使用栈也可以实现逆波兰表达式的计算，但可能需要更复杂的逻辑和额外的数据结构来模拟栈的功能。

思路：用栈来实现逆波兰表达式。遍历字符串数组，当遇到数字，则入栈；遇到运算符，则将栈顶的元素弹出作为右操作数，再将栈顶的元素弹出作为左操作数，计算完的值再入栈。

class Solution { public int evalRPN(String[] tokens) { Stack stack = new Stack(); // 遍历字符串数组 for (int i = 0; i < tokens.length; i++) { // 判断这个字符串是否为数字 // 数字难判断，但运算符很简单，因此可以转换角度来判断运算符 if (!isOperator(tokens[i])) { // 是数字就入栈 stack.push(tokens[i]); } else { // 开始运算 int y = Integer.parseInt(stack.pop()); // 右操作数 int x = Integer.parseInt(stack.pop()); // 左操作数  int result = 0; switch (tokens[i]) {  case \"+\" : result = x+y; break;  case \"-\" : result = x-y; break;  case \"*\" : result = x*y; break;  case \"/\" : result = x/y; break; } // 运算完的结果返回到栈中 Integer j = result; stack.push(j.toString()); } } // 返回栈中最后剩余的元素 return Integer.parseInt(stack.pop()); } private boolean isOperator(String s) { // 如果不是+、-、*、/，那就是数字字符 return s.equals(\"+\") || s.equals(\"-\") || s.equals(\"*\") || s.equals(\"/\"); }}

注意：我们平常写的运算表达式是属于中缀表达式，即运算符在两个运算数的中间位置，还有前缀表达式和后缀表达式。我们这里的逆波兰表达式就是后缀表达式，即运算符在两个运算数的后面，而前缀表达式就是在两个运算数的前面，也称为波兰表达式。

下面是中缀表达式转后缀表达式的详细过程：

9+(3-1) * 3+8 / 2，这个就是我们平常写的表达式。

转换成后缀表达式：
1、将所有的运算符与运算数之间加上（）。即：((9+((3-1) * 3))+(8 / 2))
2、将所有的运算符提到本级括号的外边去。即：((9((3 1)-  3)*)+(8 2) / )+
3、最后将所有的括号全部去掉，就是后缀表达式。即：9 3 1 -  3 * + 8 2 / +

按照栈的特点去计算这个表达式的过程如下： 

牛客网——JZ31 栈的压入、弹出序列

描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

1. 0<=pushV.length == popV.length <=1000

2. -1000<=pushV[i]<=1000

3. pushV 的所有数字均不相同

示例1

输入：

[1,2,3,4,5],[4,5,3,2,1]

返回值：

true

说明：

可以通过push(1)=>push(2)=>push(3)=>push(4)=>pop()=>push(5)=>pop()=>pop()=>pop()=>pop()这样的顺序得到[4,5,3,2,1]这个序列，返回true

示例2

输入：

[1,2,3,4,5],[4,3,5,1,2]

返回值：

false

说明：

由于是[1,2,3,4,5]的压入顺序，[4,3,5,1,2]的弹出顺序，要求4，3，5必须在1，2前压入，且1，2不能弹出，但是这样压入的顺序，1又不能在2之前弹出，所以无法形成的，返回false

思路：模拟第一个数组入栈出栈时的样子，与第二个数组对比，看结果是否一致。

public boolean IsPopOrder (int[] pushV, int[] popV) { Stack stack = new Stack(); int j = 0; // 将第一个数组入栈，与第二个数组进行对比，看是否一致 for (int i = 0; i < pushV.length; i++) { int x = stack.push(pushV[i]); if (x != popV[j]) { continue; } else { // 一致就继续往后比较，直至栈为空 while (!stack.empty()) {  if (stack.peek() == popV[j]) { stack.pop(); j++;  } else { break;  } } } } if (stack.empty()) { return true; } return false; }

155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

  • MinStack() 初始化堆栈对象。
  • void push(int val) 将元素val推入堆栈。
  • void pop() 删除堆栈顶部的元素。
  • int top() 获取堆栈顶部的元素。
  • int getMin() 获取堆栈中的最小元素。

示例 1:

输入：[\"MinStack\",\"push\",\"push\",\"push\",\"getMin\",\"pop\",\"top\",\"getMin\"][[],[-2],[0],[-3],[],[],[],[]]输出：[null,null,null,null,-3,null,0,-2]解释：MinStack minStack = new MinStack();minStack.push(-2);minStack.push(0);minStack.push(-3);minStack.getMin(); --> 返回 -3.minStack.pop();minStack.top(); --> 返回 0.minStack.getMin(); --> 返回 -2.

提示：

  • -231 <= val <= 231 - 1
  • pop、top 和 getMin 操作总是在 非空栈 上调用
  • push, pop, top, and getMin最多被调用 3 * 104 次

思路：既想要保持原数据不变，又要时刻维护最小数据，一个栈肯定是做不到的，要两个栈，一个普通栈，来存储元素，一个最小栈，来维护最小元素。

class MinStack { Stack stack; // 普通栈 Stack minStack; // 最小栈 public MinStack() { stack = new Stack(); // 普通栈 minStack = new Stack(); // 最小栈 } public void push(int val) { // 首先得判断这个最小栈中是否有元素。 // 如果啥也没有，那么第一个元素肯定是要入栈的 // 因为第一个元素肯定既是最大的，也是最小的 if (minStack.empty()) { minStack.push(val); } else { if (minStack.peek() >= val) { minStack.push(val); } } // 普通栈就无需判断 stack.push(val); } public void pop() { // 这里虽然删除的是普通栈的栈顶元素， // 但是如果普通栈的栈顶元素和最小栈一样， // 那么两者都得删除 // 注意：这里的比较要用 equals，下面有解释 if (stack.peek().equals(minStack.peek())) { stack.pop(); minStack.pop(); } else { stack.pop(); } } public int top() { // 这里拿的是普通栈的栈顶元素 return stack.peek(); } public int getMin() { // 这里拿的是最小栈的栈顶元素 return minStack.peek(); }}

注意：

1、这里题目明确的说了   pop、top 和 getMin 操作总是在 非空栈 上调用 。

2、这里的比较之所以要用 equals() 方法，是因为当 LeetCode 给的测试用例不在 -128~127 之间时，会分配两个不同的对象。如果我们用 == 去比较的话，肯定是 false ，因此就只有两种解决方法：1、用 equals() 方法进行比较；2、将一方进行拆包的操作之后，再去比较两者之间的关系。

下面这篇文章就讲述了 第二点中的来源：同一个数字，但不同的对象

以上就是关于栈的经典题型了。总体难度虽然用栈来解决不是很大，但是要想到用栈的知识去解决，还是挺难的。所以栈的基本知识不能，但做题想到用栈解决就很难了。

好啦！本期  数据结构之栈  的学习之旅就到此结束了！相信通过这篇文章的学习，你对栈的了解将会更进一步！我们下一期再一起学习吧！

网络标签：

相关问题