网站导航
> 技术文档 > 小h的Matlab日记——（二）矩阵的相关操作（上）

小h的Matlab日记——（二）矩阵的相关操作（上）

网友: 技术文档 2025-09-03 13:10:02

目录

一、复习一下矩阵的基础知识

（学过线性代数的朋友可以直接跳过）

二、Matlab中的向量

1、向量的创建

2、向量的调用

3、向量的修改和删除

三、Matlab中的矩阵

1、矩阵的创建

2、矩阵元素的引用

3、矩阵元素的修改和删除

香山
一、复习一下矩阵的基础知识
（学过线性代数的朋友可以直接跳过）
  • 矩阵的定义

由$m \\times n$个元素组成的$m$行$n$列的数表

\\begin{pmatrix} a_{11} & \\cdots & a_{1n} \\\\ \\vdots & \\ddots & \\vdots \\\\ a_{m1} & \\cdots & a_{mn} \\\\ \\end{pmatrix}

称为一个$m \\times n$阶矩阵，记为\\mathbf{A} = (a_{ij})_{m \\times n}。当$m = n$时，我们称矩阵为$n$阶方阵。

  • 转置矩阵

设矩阵

\\mathbf{A} = \\begin{pmatrix} a_{11} & a_{12} & \\cdots & a_{1n} \\\\ a_{21} & a_{22} & \\cdots & a_{2n} \\\\ \\vdots & \\vdots & \\ddots & \\vdots \\\\ a_{m1} & a_{m2} & \\cdots & a_{mn} \\\\ \\end{pmatrix}

则称矩阵

\\begin{pmatrix} a_{11} & a_{21} & \\cdots & a_{m1} \\\\ a_{12} & a_{22} & \\cdots & a_{m2} \\\\ \\vdots & \\vdots & \\ddots & \\vdots \\\\ a_{1n} & a_{2n} & \\cdots & a_{mn} \\\\ \\end{pmatrix}

为\\mathbf{A}的转置矩阵，记为\\mathbf{A}^\\mathbf{T}。

  • 单位矩阵

称

\\mathbf{I_n} = \\begin{bmatrix} 1 & 0 & \\cdots & 0 \\\\ 0 & 1 & \\cdots & 0 \\\\ 0 & 0 & \\ddots & \\vdots \\\\ 0 & 0 & \\cdots & 1 \\end{bmatrix}

为单位矩阵。单位矩阵一定是方阵。

  • 向量

由$n$个数构成的数表\\begin{bmatrix} a_{1} & a_{2} & \\cdots & a_{n} \\end{bmatrix}或\\begin{bmatrix} a_{1} & a_{2} & \\cdots & a_{n} \\end{bmatrix} ^ T称为$n$维行向量或$n$维列向量。显然，向量是特殊的矩阵。设向量\\mathbf{a} = \\begin{bmatrix} a_{1} & a_{2} & \\cdots & a_{n} \\end{bmatrix} ^ T，则称\\sqrt{a_1{}^2 + a_2{}^2 + \\cdots + a_n{}^2}为它的模，记为| \\mathbf{a} |。

  • 矩阵的运算

（1）加减：设矩阵\\mathbf{A} = (a_{ij})_{m \\times n}，\\mathbf{B} = (b_{ij})_{m \\times n}，则\\mathbf{A} \\pm \\mathbf{B}=(a_{ij} \\pm b_{ij})_{m \\times n}；

（2）数乘：设矩阵\\mathbf{A} = (a_{ij})_{m \\times n}，实数\\lambda，则\\lambda \\mathbf{A} = (\\lambda a_{ij})_{m \\times n}；

（3）乘法：设矩阵\\mathbf{A} = (a_{ij})_{p \\times q}，\\mathbf{B} = (b_{ij})_{q \\times s}，则\\mathbf{A} \\times \\mathbf{B} = (c_{ij})_{p \\times s}，其中c_{ij} = \\sum_{k = 1}^{q}a_{ik} \\times b_{kj}。

  • 矩阵的逆

设矩阵\\mathbf{A}为$n$阶方阵，若存在$n$阶方阵使得\\mathbf{A} \\times \\mathbf{B} = \\mathbf{B} \\times \\mathbf{A} = \\mathbf{I_{n}}，则称矩阵\\mathbf{B}为的\\mathbf{A}逆，记为\\mathbf{B} = \\mathbf{A} ^{-1}。

  • 特征值和特征向量

设矩阵\\mathbf{A}为$n$阶方阵，若存在\\lambda \\in C和非零$n$维列向量，使得\\mathbf{A} x = \\lambda x成立，则称数\\lambda是方阵\\mathbf{A}的特征值，列向量x是方阵\\mathbf{A}对应\\lambda的特征向量。显然，特征向量不唯一，$kx (k \\neq 0)$也是方阵对应的特征向量。

二、Matlab中的向量
1、向量的创建

（1）直接声明：元素之间用空格或逗号隔开是行向量，

a = [1 2 3 4 6]b = [1,2,4,5,6]

 元素之间用分号或回车隔开是列向量。

c = [1;2;3;4;5]d = [1234]

也可以声明一个空向量。

e = []

以上五个向量声明的结果为

 

 （2）冒号法声明一个行向量：这种声明方式的语法为

%% A : step : B

 A是向量的第一个元素，step是相邻元素的差值，当step为正时向量的最后一个元素不大于B，当step为正时向量的最后一个元素不大于B。以下是示例：

a = 1 : 2 : 9b = 2 : 3 : 15

 当step = 1时，可以简写为

%% A : B

例如：

c = 1:10d = 10 : -2 : 3

 当step=0或 0 \\\\ A > B \\end{cases}\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?%5Cbegin%7Bcases%7D%20step%20%3E%200%20%5C%5C%20A%20%3E%20B%20%5Cend%7Bcases%7D\" />时，该向量为空向量,例如：

e = 5 : 2 : 1f = 10 : 0 : 100

 以上向量的运算结果为

（3）使用函数声明：

 linspace函数可用于声明等差数列行向量的声明，它的语法为

%% linspace(A,B,n)

 A是向量的第一个元素，B是向量的最后一个元素，n是向量中元素的个数

a = linspace(1,10,5)b = linspace(6,1,6)

 当$n = 100 $时，参数可以省略，它的语法为

%% linspace(A,B)c = linspace(1,10)

 以上三个向量运算的结果为

 logspace函数可用于声明等比数列行向量的声明，它的语法为

%% logspace(A,B,n)

 向量的第一个元素为$10 ^ A$,向量的最后一个元素为$10 ^ B$，$n$是向量中元素的个数

a = logspace(1,2,5)b = logspace(log10(2),log10(1024),5)c = logspace(log10(2),5 * log10(2),5)

当$n = 50 $时，参数$n$可以省略，它的语法为

%% logspace(A,B)

以上三个向量运算的结果为

 

 

2、向量的调用

我们可以调用length函数或numel函数来计算向量中元素的个数。

a = 1 : 3 : 20;x_a = length(a)b = [2,3,4,5];x_b = numel(b)

 注意：与C语言不同的是，在Matlab中，向量元素的索引（下标）是从1开始的！

（1）单个元素的调用

调用数组a中下标为ind的元素的语法为

%% a(ind)

其中，ind必须是合法的逻辑值或正整数，示例：

b = [2,3,4,5];h = b(3)

空向量的调用索引也是空。

a = [];a([])

以上向量运算的结果为

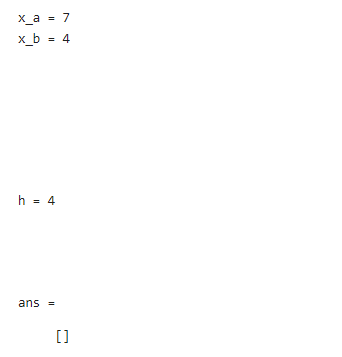
（2）多个元素的调用

将ind设置成一个向量即可，语法同上。以下是示例：

a = logspace(log10(2),log10(1024),10);ind = 1 : 2 : 9;h = a(ind)a([2 2 4 4])

此外，也可以使用关键字end代表向量的最大索引。示例：

p = a(end)q = a(end : -2 : 1)

 以上向量运算的结果为

有一点值得注意：end关键字不能用于赋值，例如：

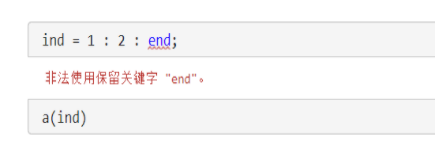
3、向量的修改和删除

调用向量的某些元素直接赋值即可修改对应的值，赋值为空即可将对应位置的元素删除。

a = logspace(log10(2),log10(1024),10);a(1) = 1a([end - 1,end]) = []

若赋值号右侧是一个数字的话，对应位置的元素全部修改为这个数。

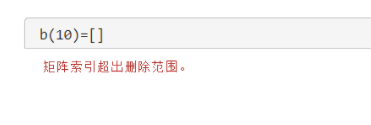
a([end - 1,end]) = 123

 注意下面这种情况：

b = logspace(log10(2),log10(8),3);b(5) = 10

 以上向量运算的结果为

观察b向量的运算结果可以发现能用这样的方法增加向量的长度，也就是说可以越界修改，但不可以越界删除。

三、Matlab中的矩阵

向量可以看成是特殊的矩阵。

1、矩阵的创建

（1）直接输入法：按照先行后列的顺序输入矩阵的元素即可。同行元素用逗号或空格隔开，列与列之间用分号或回车隔开即可。

a = [1,2,3;4,5,6]b = [1,2,3; 6,7,8]

 这两个矩阵运算的结果为

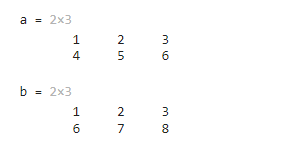
（2）使用函数创建矩阵：

第一组：
zeros函数可以创建一个全为0的矩阵，ones函数可以声明一个全为1的矩阵，eye函数可以声明一个单位对角矩阵，

a = zeros(3)b = zeros(3,2)c = ones(3)d = ones(3,2)e = eye(3)f = eye(3,2)

 以上3个函数使用非常普遍，需要熟练记忆。以上声明的结果为

第二组：
rand函数用来创建区间0和1之间的均匀分布随机数矩阵，randi函数用来创建随机分布的均匀整数矩阵，随机数的分布区间为[imin,imax]，生成的矩阵为$m \\times n$矩阵。它的语法为

%% randi([imin,imax],m,n)

若$ imin = 1$，则它的语法可以简写为

%% randi(imax,m,n)

若$m = n$，它的语法可以简写为

%% randi([imin,imax],m)

以下是示例：

a = rand(4)b = rand(4,3)c = randi([1,50],4,3)d = randi(6,1,4)

randn函数用来创建标准正态分布的随机数矩阵，标准正态分布即以0为平均数，1为标准差的正态分布，记为$N(0,1)$。

e = randn(4)f = randn(3,4)

这些矩阵的元素都是随机数，因此每次运行的结果都不尽相同，这里就不给出运行的结果了。感兴趣的小伙伴可以多次运行以下这四行代码，观察一下输出结果。以上3个函数常用于解决分布类问题，应用也很广泛。

第三组：

diag函数可用来创建对角矩阵或获取矩阵的对角元素。如果输入的第一个参数是向量，则表示创建一个对角矩阵，它的语法为

%% diag(A,k)

k=0 表示主对角线，0\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?k%3E0\" />位与主对角线上方，<img alt=\"k位与主对角线下方。

a = diag([1,2,3],2)b = diag([2,3,4],0)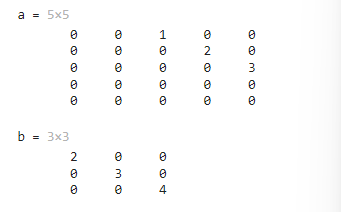

 若第一个参数是一个矩阵，则该函数返回这个矩阵第k条对角线上的元素组成的列向量

a = diag([1,2,3; 4,5,6; 7,8,9],1)a = diag([1,2,3; 4,5,6; 7,8,9],-1)

 

当k=0时可以省略

b = diag([1,2,3,4])a = diag([1,2,3; 4,5,6; 7,8,9])

 

blkdiag函数用于生成分块对角矩阵，且不限制参数的个数

a = [1,2,3; 4,5,6];b = [1,2; 3,4];c = blkdiag(a,b)

 

（3）从其他文件中导入到Matlab中：这一部分放在导入数据中介绍。

2、矩阵元素的引用

（1）双索引引用：矩阵\\mathbf{A} = (a_{ij})_{m \\times n}第i行第j列的元素表示为a_{ij}。对矩阵元素第调用与向量相似。它的语法为

%% a(row_ind,column_ind)

它的行索引和列索引都可以是整数或向量。

a = randi([2,10],5)x12 = a(1,2)x = a(2,end)y = a(3,[1,3,5])z = a(1:2:end,1:2:end)

以下是输出结果的一个示例。 

 

我们可以用以下语句取矩阵某一行或某列的全部元素：

r1 = a(3,1:end)c1 = a(1:end,2)

这两个语句可以简写为

r1 = a(2,:)c1 = a(:,3)

 可以理解为冒号是1:end的省略。以下是输出结果的一个示例。 

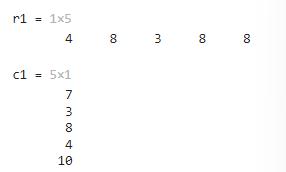
 我们可以用size函数来求一个矩阵的大小，它的语法为

%% size(A,d)

当d=1时，返回矩阵的行数；当d=2时，返回矩阵的列数。 若省略参数d，则返回这个矩阵的维度向量，

a = randi([2,10],4,5);dim = size(a)[r,l] = size(a)r = size(a,1)l = size(a,2)

以下是计算的结果。

 

 

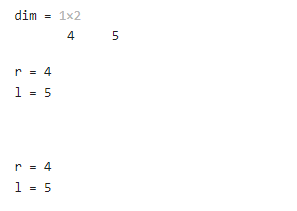
（2）length函数和numel函数：
length函数和numel函数的参数也可以是矩阵，length函数返回矩阵行和列中较大的值，numel函数返回矩阵元素的总数。

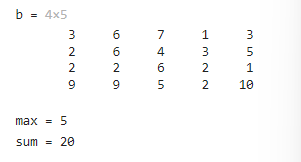
b = randi(10,4,5)max = length(b)sum = numel(b)

以下是输出结果的一个示例：
 

（3）线性索引：
Matlab中，矩阵的元素是以单列的顺序储存在内存中的。因此可以按列将矩阵的元素排序，使用单索引调用。

b = randi(100,4,5)x1 = b(5)x2 = b(2:7)x3 = b(:)x4 = b(1:end)

 对向量元素的调用也可以理解为线性索引。以下是运算结果的一个示例。

 此外，sub2ind函数和ind2sub函数可以实现矩阵元素原始索引（双下标）和线性索引的转换，语法如下：

%% sub2ind([r,l],x_row,x_col)

 [r,l]表示矩阵的大小，x_row和x_col表示目标元素的双索引，函数的返回值为该元素的线性索引，

%% ind2sub([r,l],ind)

 [r,l]表示矩阵的大小,ind表示目标元素的线性索引，函数返回该元素的原始索引。

ind = sub2ind([4,5],2,3)[x,y] = ind2sub([4,5],10)

 以上这个两个函数运行的结果为

 

3、矩阵元素的修改和删除

我们可以直接复制修改矩阵被引用位置的元素，与向量相似，

a = [1:4; 2:5; 6:9]a(2,3) = 10a(3,:) = 100a([1,3],[2,4]) = [12 14;22,24] %要注意左右两侧矩阵的大小要匹配

以下是这四个矩阵运算的结果：

 

也可以通过线性索引进行修改，

a(1:2:end) = 100a(4) = 1234a([1 3 4 6]) = [-1 -2 -3 -4]

 以下是这三个矩阵运算的结果：

 

 与向量相同，对矩阵也允许越界修改，效果是对矩阵进行拓展。

a(4,5) = 45a(4:5,5:6) = -5

  以下是这两个矩阵运算的结果：

 

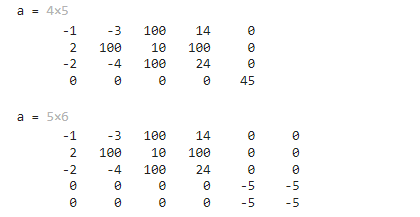
将矩阵某位置的元素赋值为空，即可实现删除该元素。但通常只能删除整行或整列,

a = [1:4;2:5;3:6]a(:,1) = [] 

想要删除某一个元素，可以引用其线性索引进行空赋值，然后该矩阵的其他元素会按照线性索引的顺序排成一个行向量，

a([1 2 3]) = []

  以下是这三个矩阵运算的结果：

以上便是本篇文章的全部内容。后续会不断补充完善，敬请期待！如有勘误请联系作者！

网络标签：

相关问题