leetcode-代码随想录-动态规划-1049最后一块石头的重量 II

题目

题目链接：1049. 最后一块石头的重量 II - 力扣（LeetCode）
有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，**最多只会剩下一块 **石头。返回此石头 **最小的可能重量 **。如果没有石头剩下，就返回 0。

输入：stones = [2,7,4,1,8,1]输出：1解释：组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

class Solution {public: int lastStoneWeightII(vector<int>& stones) { }};

思路

01背包问题：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

问题转化：

• 每次粉碎石头相当于 两堆石头的重量相减，最终目标是让剩下的石头重量最小。
• 就等价于 将石头分成两堆，使两堆的重量差最小
• 问题转化为：
  • 计算所有石头的总重量 sum；
  • 找到一个子集，使其重量最接近 sum / 2（target）；
  • 最终的最小重量：sum - dp[target] - dp[target]；

转化为背包问题：

• 背包容量：target = sum / 2
• 物品：石头stone[i]
• 物品重量：stone[i]
• 物品价值：stone[i]
• 目标：在不超过 target 的情况下，尽可能装满背包；

416-分割等和子集是求背包是否正好装满，而本题是求背包最多能装多少。

1. DP数组含义

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。

2. 递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题则是：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])

3. DP数组初始化

既然 dp[j]中的j表示容量，那么最大容量（重量）是多少呢，就是所有石头的重量和。

因为提示中给出1 <= stones.length <= 30，1 <= stones[i] <= 1000，所以最大重量就是30 * 1000 。
而我们要求的target其实只是最大重量的一半，所以dp数组开到15000大小就可以了。

dp[j]都初始化为0就可以了。

4. 确定遍历顺序

如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

for (int i = 0; i < stones.size(); i++) { // 遍历物品 for (int j = target; j >= stones[i]; j--) { // 遍历背包 dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]); }}

5. 打印DP数组

举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：

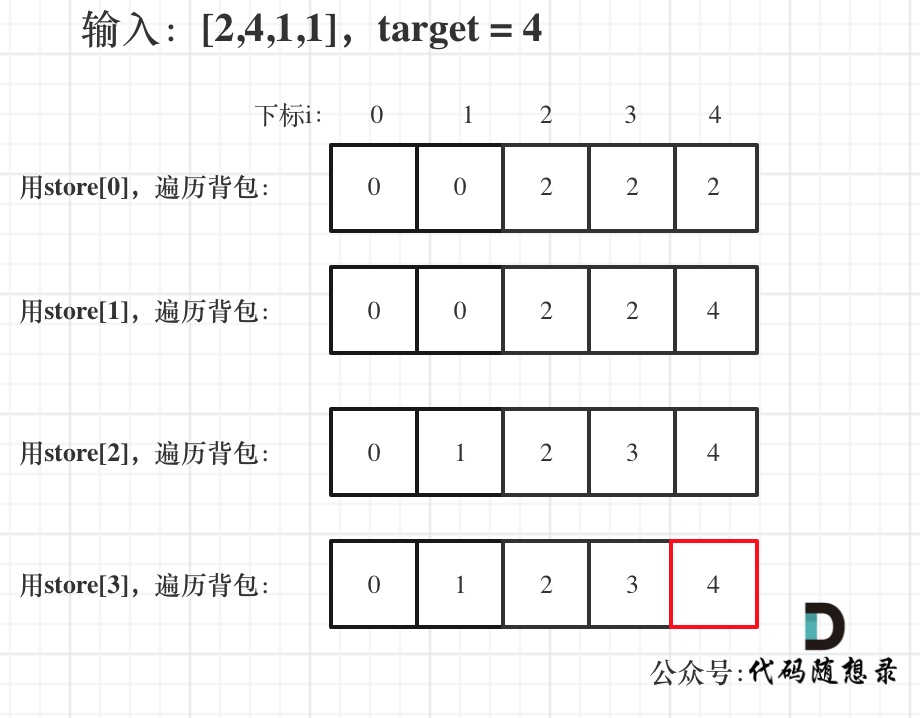
最后dp[target]里是容量为target的背包所能背的最大重量。

那么分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]。

在计算target的时候，target = sum / 2 因为是向下取整，所以sum - dp[target] 一定是大于等于dp[target]的。

那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。

#include #include #include #include #include using namespace std;class Solution {public: int lastStoneWeightII(vector<int>& stones) { int sum = 0; for(int i = 0; i < stones.size(); i++){ sum += stones[i]; } int target = sum / 2; vector<int> dp(15000, 0); // 遍历：先物品，再背包 for(int i = 0; i < stones.size(); i++){ for(int j = target; j >= stones[i]; j--){ dp[j] = max(dp[j], dp[j-stones[i]]+stones[i]); } // 打印dp for(int k = 0; k <= target; k++){ cout << dp[k] << \" \"; } cout << endl; } return sum - dp[target] - dp[target]; }};vector<int> inputvector(){ string line; getline(cin, line); istringstream iss(line); vector<int> vec; int num; while(iss >> num) { vec.push_back(num); } return vec;}int main(){ cout << \"stones: \"; vector<int> stones = inputvector(); Solution obj; int res = obj.lastStoneWeightII(stones); cout << \"res: \" << res << endl; return 0;}

例1：

stones: 2 7 4 1 8 10 0 2 2 2 2 2 2 2 2 2 2 0 0 2 2 2 2 2 7 7 9 9 90 0 2 2 4 4 6 7 7 9 9 110 1 2 3 4 5 6 7 8 9 10 110 1 2 3 4 5 6 7 8 9 10 110 1 2 3 4 5 6 7 8 9 10 11res: 1

例2：

stones: 2 4 1 10 0 2 2 20 0 2 2 40 1 2 3 40 1 2 3 4res: 0