数学建模：评价决策类问题_决策数学建模代码

这里需要注意的就是四个指标类型转换的函数，因为在大多数评价决策类问题中都会涉及到先将指标统一转成极大型。

这里就是展示原始数据。

通过计算得分可以发现第2个对象是最优方案。

三、熵权法

1.适用场景

不管是在层次分析法，还是在TOPSIS法中，权重的求解都是相对主观的，此时就可以用熵权法求解更客观的权重。熵权法常和TOPSIS法结合，为TOPSIS求出权重。

2.基本概念

对于某个指标，可以用“信息熵”来衡量其数据的离散程度。其信息熵值越小，离散程度越大，则该指标的权重越大。若某个指标的值全部相等，则该指标在这个评价中不起作用。举个例子，假如汉堡和拉面的价格很接近，那么价格这个指标在我的决策中的权重必然会更小，我在决定吃哪个时更倾向于考察其他的指标而非价格指标。所以熵权法是一种客观的赋权方法，它只依赖数据本身得出权重。

3.基本步骤

（1）原始矩阵正向化，正向矩阵标准化

跟TOPSIS一样，不多说了。

（2）计算概率矩阵P

概率矩阵说白了就是求每个元素的数值在当前指标下所占比例，即数值除以其列向量的累加和，跟TOPSIS法里最后计算得分的归一化一致。

（3）计算熵权

对于第j个指标，信息熵的计算公式为  。当一列里所有元素都等于1/n时，此时信息熵为1最大，则该指标不起作用。再定义信息效用值，效用值越大，权重越大。最后将信息效用值归一化就能得到熵权w。

4.代码

由于例子和TOPSIS法里的一样，所以就是直接把TOPSIS法里求出的正向矩阵拿过来直接用了。

通过熵权法就求出了四个指标的权重，一般这一步是用在TOPSIS法计算得分前，为各个指标提供权重。

四、模糊综合评价模型

1.适用场景

对于像身高体重这种拥有确定数据的指标，因为可以通过精准测量得到，所以称为确定性概念。但对于大小，长短等概念，由于没有一个确切的概念，所以称为模糊性概念，此时抽象出的模型就是模糊性模型。

2.模型概念

首先需要声明模糊集合和隶属函数这两个概念。

对于经典的集合，每个元素只存在属于和不属于两种状态。此时集合A的特征函数，对于任意的x，f(x)只等于0或1,0表示不属于集合A，1表示属于集合A。

而模糊集合有所不同，模糊集合承认一个元素处于属于和不属于的叠加态。所以此时对于模糊集合A，可以用隶属函数来刻画一个元素在这个模糊集合里的状态。此时对于任意的x，其隶属函数值处于[0,1]这个区间上，表示隶属度。若函数值等于1说明绝对属于该集合，等于0说明绝对不属于该集合，而在0和1之间处于属于和不属于的叠加态，当函数值等于0.5时说明模糊程度最高，数值越大越属于这个集合。

举个例子，我们定义“年轻”这个概念A=“年轻”，X表示年龄的集合，属于0到100岁。此时我们就可以定义隶属函数，因为小于20岁肯定是年轻，大于40岁基本上也和年轻没关系了，但在20到40岁之间不一定。其中范围和函数的定义可以随意构造，也可以根据一些其他指标进行定义，比如可以用恩格尔系数定义“小康家庭”的隶属函数。

模糊集合A可以由一个向量表示，其中的分量数为X中元素的个数，每个分量的数值为该元素的隶属度。而当X为无限集合时，模糊集合A可以表示为。注意，这里的除不是表示分数，而是表示x的隶属度，其中根据范围的构造可以写成分段积分的形式。

和TOPSIS法中指标类型类似，模糊集合也分为偏小型，中间型和偏大型，可以理解为隶属函数的单调性。

3.评价方法

在模糊综合评价中，需要引入三个集合，分别为因素集U，评语集V和权重集A。因素集包括所有评价的指标。评语集包括能得出的评价结果，比如“优秀”“良好”等，或者所有待决策的方案。权重集包括所有指标的权重。所以在评价或决策时，就是通过隶属函数计算评语集中所有元素的隶属度，从而确定哪个元素最符合或最优。

4.一级模糊综合评价模型

对于指标较少的评价，就可以用一级模糊综合评价模型。

在确定三个集合后，就需要确定模糊综合判断矩阵R，其中R的行数为指标数，列数为评语数，第i行第j列的元素表示在第i个指标被评为第j个评语的隶属度。

而对于隶属度的确定，可以自己构造隶属函数，也可以使用模糊统计法。举个例子，模糊统计法就是，假如由群众打分来确定每个员工的政治表现，那么对于政治表现这个指标，若有10%的人认为该员工优秀，那么员工在政治表现这个指标，被评为优秀的隶属度就是0.1，即选择这个评语的人数比例。

之后进行模糊合成运算，将权重集A看作一个向量，与模糊关系矩阵进行合成运算，得到综合评价结果向量B，B的每个元素表示对象整体被评为某个评语的隶属度。其中，合成运算有多种方法，这里一般采用统筹兼顾的矩阵乘法。

最后，可以取结果向量B中的最大值为评价结果，也可以多个指标进行加权求结果。

5.多层次模糊综合评价模型

这玩意儿看数学表达式是真抽象，但举个例子就能发现根本没那么难理解。

多层次模糊综合评价模型就是当指标非常多时，可以根据隶属关系划分层次，然后分层求解。

举个例子，若要评价一个外卖店铺的好坏，会有非常多的评价指标，那么我们可以先把“食物味道”“服务质量”和“价格”这三个指标提出来作为第一层的指标，然后将“客人评价”“出餐速度”和“店铺卫生”这三个指标作为第二层指标。这里，第一层指标为上级指标，第二层指标为下级指标。

那么计算方法就是从底到顶，先将第一层的三个指标分作为第二层的评价对象，然后分别对这三个指标用三次一级模糊综合评价，这样就能求出这三个上级指标的综合评价结果向量B。接着将用这三个指标的B向量构成对于总的评价对象店铺的模糊综合判断矩阵R的行向量，然后再用一次一级模糊综合评价就能求出对店铺的评价。

在这个例子中，指标被分为了两层，那么这就是一个二层模糊综合评价模型，也可以根据情况将指标分为更多层。

6.代码

import numpy as np#一级模糊综合评价#运行费用#模糊综合判断矩阵R：R23=np.array([ [0.18,0.14,0.18,0.14,0.13,0.23], [0.15,0.20,0.15,0.25,0.10,0.15], [0.25,0.12,0.13,0.12,0.18,0.20], [0.16,0.15,0.21,0.11,0.20,0.17], [0.23,0.18,0.17,0.16,0.15,0.11], [0.19,0.13,0.12,0.12,0.11,0.33], [0.17,0.16,0.15,0.08,0.25,0.19]])#权重集A23=np.array([0.20,0.15,0.10,0.10,0.20,0.15,0.10])#评价结果#np.dot计算向量点乘或矩阵乘法B23=np.dot(A23,R23)print(\"一级模糊综合评价结果：\\n\",B23)#二级模糊综合评价#产品情况R1=np.array([ [0.12,0.18,0.17,0.23,0.13,0.17], [0.15,0.13,0.18,0.25,0.12,0.17], [0.14,0.13,0.16,0.18,0.20,0.19], [0.12,0.14,0.15,0.17,0.19,0.23], [0.16,0.12,0.13,0.25,0.18,0.16]])#权重集A1=np.array([0.15,0.40,0.25,0.10,0.10])#评价结果B1=np.dot(A1,R1)print(\"产品情况的二级模糊综合评价结果：\\n\",B1)#销售能力R2=np.array([ [0.13,0.15,0.14,0.18,0.16,0.25], [0.12,0.16,0.13,0.17,0.19,0.23], B23, [0.14,0.13,0.15,0.16,0.18,0.24], [0.16,0.15,0.15,0.17,0.18,0.19]])#权重集A2=np.array([0.2,0.15,0.25,0.25,0.15])#评价结果B2=np.dot(A2,R2)print(\"销售能力的二级模糊综合评价结果：\\n\",B2)#市场需求R3=np.array([ [0.15,0.14,0.13,0.18,0.14,0.26], [0.16,0.15,0.18,0.14,0.16,0.21]])#权重集A3=np.array([0.55,0.45])#评价结果B3=np.dot(A3,R3)print(\"市场需求的二级模糊综合评价结果：\\n\",B3)#三级模糊综合评价R=np.array([B1,B2,B3])A=np.array([0.4,0.3,0.3])B=np.dot(A,R)print(\"产品的三级模糊综合评价结果：\\n\",B)

在向上的过程中，只需要将下层计算出的评价结果向量当作判断矩阵的行向量传入即可。

其中每个数组里的最大值对应的评语即为最终评价。

五、灰色关联分析模型

0.灰色系统和关联分析

用颜色深浅反应信息的多少，颜色越深信息越少。若一个系统是黑色的，说明信息量太少；若是白色的说明信息量充足；而处于黑白之间的灰色系统则说明信息不完全。

关联分析就是分析在一个系统中，哪些因素是主要的，哪些因素的次要的；哪些明显，哪些潜在；哪些是需要发展的，哪些是需要抑制的。如果使用数理统计法，当面对数据灰度大，即信息不完全的情况效果就不是很明显了。

1.适用场景

灰色关联分析可以不受样本量多少和样本有无规律的限制，在面对信息不完全的情况时会有很大作用。灰色关联分析的思想就是根据序列曲线几何形状的相似程度来判断关系是否紧密。曲线越接近，关联度越大。灰色关联分析也常与TOPSIS法结合，减少主观设定母序列的偏差。

2.基本步骤

（1）构造母序列和子序列

母序列Y就是能反应系统特征的序列，记为一个列向量，行数n为系统的特征数。

子序列X就是影响系统的因素，记为一个矩阵，这里矩阵X的列数m为因素数，行数n为特征数，即母序列的行数。为了方便后续求解，此时可以将母序列和子序列矩阵拼接，让母序列作为矩阵的第零列。

举个例子，假如要分析工农业谁对国民生产总值的影响更大，若给出了国民生产总值，农业和工业作为三行的表格，那么就可以定义国民生产总值这一行为母序列，再把矩阵转置即可。

灰色关联分析用在评价决策类问题中，在正向化后，可以定义母序列的行数为方案数，其元素为每个方案的所有指标的最大值。此时可以发现，母序列就是TOPSIS法中的正理想解。

（2）数据预处理

这里首先还是要对母序列和子序列的各个数据进行去量纲操作，但和归一化不同，这里是要计算每个指标的平均值，然后每个元素除以对应的平均值，即均值化。

（3）计算灰色关联系数和关联度

灰色关联系数可以反应子序列中各个指标与母序列的关联程度。首先需要计算两级最小差a和两级最大差b。两级最小差就是拿第零列的母序列依此和后续的子序列的列向量构成一组，每组里相同特征的两个元素取绝对差，然后取这一组绝对差的最小值，最后再取所有组中最小值的最小值即为两级最小差。两级最大差同理。

之后构造第i个指标第k个特征的关联系数，其中一般取。

所以第i个指标的关联度，最大值即为最相关的指标。

（4）计算指标权重

每个指标的权重就是对关联度进行归一化，即对应的关联度除以所有关联度的累加和。最后就可以计算得分并归一化求最终比例。

所以灰色关联分析就是通过求解每个指标对特征的关联大小，然后让关联度大的拥有大的权重，说白了还是一个求权重的方法。

3.代码

（1）灰色关联分析

import numpy as np#读取初始矩阵A=np.array(eval(input(\"输入初始矩阵：\\n\")))#注意，如果指标类型不为极大型，还需要正向化#每个指标的平均值Mean=np.mean(A,axis=0)#每一列#均值化A_Mean=A/Meanprint(\"均值化后的矩阵：\\n\",A_Mean)#母序列Y=A_Mean[:,0]#第0列#子序列X=A_Mean[:,1:]#从第一列开始往后#计算|X0-Xi|矩阵#X.shape[1]返回矩阵X的列数absX0_Xi=np.abs(X-np.tile(Y.reshape(-1,1),(1,X.shape[1])))#两级最小差a=np.min(absX0_Xi)#np.min直接求最小值#两级最大差b=np.max(absX0_Xi)#关联系数co=(a+0.5*b)/(absX0_Xi+0.5*b)#关联度degree=np.mean(co,axis=0)print(\"各指标的灰色关联度：\\n\",degree)

如果有需要还可以加上对关联度归一化求权重的代码。

（2）灰色关联评价

这就是加上后续求权重和得分的完整代码。

前面和TOPSIS法一样，无非就是后面用灰色关联分析求出了权重，然后根据权重计算的得分。

六、主成分分析（PCA）

1.适用场景

在实际问题中，一个系统的变量往往会非常多，此时就需要对这些变量进行降维，只保留原始变量的关键信息。举个例子，在买衣服时，影响的变量其实有很多，比如身高，体重，臂展，肩宽等等。但在对这些变量进行降维后，我们就可以用尺码这一个变量进行决策。

主成分分析就是将重复的变量删去建立较少能保留原始信息的互不相关的新变量。说白了就是找到一个投影矩阵，然后对一个原始矩阵进行投影，从而构造出一个新矩阵。其各个列向量相互线性独立，所以能张成一个远小于原矩阵空间的新空间，这些列向量就是新空间里的主成分，即变换后的坐标轴。

2.基本步骤

（1）原始矩阵标准化

首先，需要对原始矩阵进行标准化处理。这里的标准化方法就是让每个元素等于其减去这一列所有元素的平均值再除以标准差，得到标准矩阵X。注意这里除以的标准差为样本标准差，在python中需要在np.std函数中传入ddof=1这个参数。

（2）计算协方差矩阵（样本相关系数矩阵）

协方差矩阵R的计算方法就是。简而言之，协方差矩阵就等于标准矩阵R的转置乘以R再除以n-1，形式类似线性代数里最小二乘法中的A转置乘以A。

（3）计算R的特征值和特征向量并按特征值从大到小排序

在计算协方差矩阵R的特征向量后，每个特征向量即对应一个主成分。这里，特征值越大说明数据的方差越大，携带了越多的信息。

（4）计算主成分贡献率及累计贡献率

贡献率，即每个主成分的贡献率为第j个特征值除以所有特征值的累加和。第j个主成分的累计贡献率就是把前j个贡献率的前缀和。这里也可以将贡献率作为主成分的权重进行后续求解。

（5）写出主成分并分析其意义

主成分就是原始数据在该特征向量方向上的投影坐标值。一般来说，我们取前若干个主成分的累计贡献率超过百分之八十的特征值所对应的主成分，生成主成分得分矩阵T。T为标准矩阵X乘以特征向量矩阵。其中第i个主成分为标准矩阵X乘以其特征向量，即特征向量在每个指标上的分量乘以该指标的列向量后求和。

对于某个主成分而言，需要分析其代表的意义，解释其现实含义。组成该主成分的指标前的系数越大，即特征向量在这个指标上的分量越大，说明该指标对该主成分的影响越大。这里的解释千人千面，可以靠主观直觉，也可以靠查阅一些文献。

太抽象了……

（6）根据主成分结果做后续分析

这里的后续分析一般有主成分得分，聚类分析，回归分析等。

3.代码

import numpy as npimport pandas as pd#导入线性代数的计算库from scipy import linalgdf=pd.read_excel(\'棉花产量.xlsx\',\'Sheet1\',usecols=\'B:F\')#只读B到F列#print(df)#将DataFrame类型转成数组x=df.to_numpy()print(x)#标准化#ddof=1为计算样本标准差，默认为0总体标准差X=(x-np.mean(x,axis=0))/np.std(x,ddof=1,axis=0)#计算协方差矩阵#cov计算协方差 -> 输入转置R=np.cov(X.T)#计算特征值和特征向量#linalg.eigh求出的特征值从小到大排序eig_val,eig_vec=linalg.eigh(R)#降序排列eig_val=eig_val[::-1]#-1为步长 -> 反转eig_vec=eig_vec[:,::-1]#特征向量矩阵按列降序排列#计算主成分的贡献率和累计贡献率contribution_rate=eig_val/sum(eig_val)#comsum计算前缀和sum_contribution=np.cumsum(contribution_rate)print(\"特征值：\\n\",eig_val)print(\"特征向量：\\n\",eig_vec)print(\"贡献率：\\n\",contribution_rate)print(\"累计贡献率：\\n\",sum_contribution)

要注意的就是在计算协方差矩阵时用的是样本标准差。

由图可得，如果取前百分之八十的话，那第一个主成分就够用了。 

七、聚类分析

1.适用场景

一般聚类分析的作用就是将复杂的数据分组简化后再进行后续计算。

2.基本概念

聚类是一种无监督的学习方法，这里的无监督是指不依赖某个标准，只依赖数据本身。聚类的过程就是将一个数据集划分为若干组（class）或类（cluster）的过程，使得同一组里的对象有较高的相似度，不同组的对象不相似。这里相似与不相似是由各对象之间的距离决定的，距离越大，相似度越高。在聚类时应满足最大化类内的相似性，同时最小化类间的相似性。

聚类分析分为对样品分类的Q型聚类和对指标分类的R型聚类。其中Q型聚类的应用较多。Q型聚类的主要作用就是综合多个指标对样本进行分析，R型聚类的作用和主成分分析类似，就是将多个指标进行降维。

对于距离，大多数情况下用的都是欧氏距离。而对于两个类的类间距离，存在最短距离和最长距离。最短距离就是两类中任意不同类对象间距离的最小值，最长距离类似。此外，还存在重心距离，即两类中所有对象的平均值的距离。

3.谱系聚类（层次聚类）法的步骤

（1）选择样本距离和类间距离的定义并计算距离矩阵

这个就是从上述说的距离定义中选一个，然后计算出各个样本构成的距离矩阵D。这里距离矩阵D可以理解为邻接矩阵，为一个对称方阵且对角线元素均为0。

（2）按类间距离定义合并

在构建完距离矩阵后，此时每个元素可以看作自己就是一个类。那么之后就是每次都寻找非零元素里的最小值Dij，表示第i个样本和第j个样本距离最近，即可以合并为一个新类。之后再从距离矩阵中删除第i个样本和第j个样本所在的行和列，并加入合并成的新类和其他类的最短距离，构成新的距离矩阵。重复上述过程直到只剩一个类为止。

最小生成树……是你吗……

（3）画出聚类图并决定类的个数

聚类图其实就是一棵二叉树，而类的个数就可以在合并时创建一个表记录，要求有几类直接从表里查即可。

（4）代码

import numpy as npimport matplotlib.pyplot as plt#计算谱系聚类的模块#linkage返回一个(n-1)*4的连接矩阵，其中n为样本数，每行表示一次合并#第0列和第1列：被合并的两类#第2列：距离#第3列：新类大小#dendrogram绘制树状图from scipy.cluster.hierarchy import linkage, dendrogram#原始矩阵 -> 5*2data = np.array([ [0, 0], [1, 0], [5, 0], [5, 1], [10, 0]])#合并后的连接矩阵#类间距离为最短距离 -> 单连接谱系聚类#编号0~n-1为原始点，n~2n-2为新类dis = linkage(data, method=\'single\')print(\"聚类过程矩阵：\")#enumerate遍历连接矩阵的的每一行，即第i次合并操作的四个数据rowfor i, row in enumerate(dis): print(f\"第{i+1}次合并: {int(row[0])} 和 {int(row[1])} 合并，距离为 {row[2]:.2f} ，新类大小 {int(row[3])}\")# 绘制树状图#使用中文字体from matplotlib.pylab import mplmpl.rcParams[\'font.sans-serif\'] = [\'SimHei\']mpl.rcParams[\'axes.unicode_minus\'] = Falseplt.figure(figsize=(10, 5))dendrogram( dis,#连接矩阵 labels=[\'A\', \'B\', \'C\', \'D\', \'E\'],#标签 orientation=\'top\',#从顶到底往下扎 distance_sort=\'descending\',#按距离从大到小排序叶节点 show_leaf_counts=True,#展示类大小)# 添加网格线plt.grid(axis=\'y\', linestyle=\'--\', alpha=0.5) # 只在Y轴方向添加虚线网格，透明度50%#标签plt.title(\'单连接谱系聚类树状图\')plt.xlabel(\'数据点\')plt.ylabel(\'距离\')plt.show()

注意这里选择的单连接就是用最短距离衡量类间距离。

聚类过程矩阵反应的是每一步合并的类。

这张图就是将聚类过程以树状图的形式展示出来，其中可以通过确定类间距离从而确定类的个数。

4.K-Means算法的步骤

K-Means算法，即K-平均算法会把样本分为k个类。和谱系聚类法不同，K-Means法中以类中对象的平均值来衡量相似度，最终输出方差最小，即类内高相似度的k个聚类。

（1）选择任意k个样本作为初始聚类

K-Means算法首先就是随便选k个样本，让它们自己构成一个类，那么此时就产生了k个类。

（2）对剩余样本进行聚类

之后，对剩余的每个样本都求到上述k个类的距离，然后找出其到这k个类距离的最小值，把该样本划分到离它最近的这个类里。最终，所有样本都被划分到这k个类中。

（3）更新聚类中心并重新划分

在k个类划分完成后，就要重新计算每个类中所有样本的平均值作为这个类的中心。接着将这k个中心点看作新的k个类，重复（2）（3）步，直到每个聚类不再发生变化为止。

由过程可以看出，K-Means算法因为涉及求平均值，所以对偏离点很敏感。一旦有个偏离点距离类特别远，那么求平均值后的类中心也会产生很大偏移。

（4）代码

deepseek老师教的比网课还详细……

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.cluster import KMeans#自定义图表颜色from matplotlib.colors import ListedColormap#使用中文字体from matplotlib.pylab import mplmpl.rcParams[\'font.sans-serif\'] = [\'SimHei\']mpl.rcParams[\'axes.unicode_minus\'] = False#原始数据data = np.array([ [1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])print(\"原始矩阵：\\n\", data)#创建KMeans模型kmeans = KMeans( n_clusters=2, # K random_state=42 # 确保每次选择相同的初始点)# 拟合数据kmeans.fit(data)# 获取结果print(\"类中心:\\n\", kmeans.cluster_centers_)print(\"数据点标签:\", kmeans.labels_)print(\"新数据点预测:\", kmeans.predict([[0, 0], [4, 4]]))#预测这两个点所属的类#可视化#设置图表大小plt.figure(figsize=(12, 10))#1.绘制原始数据点和类中心的图像plt.subplot(2, 2, 1)#创建2*2多图中的第一个图 -> 左上#两个类的信息表colors = [\'red\', \'blue\'] # 设置两个类的颜色markers = [\'o\', \'s\'] # 设置不同类的形状 -> 圆圈和方框#绘制数据点for i in range(2):#遍历每个类 cluster_data = data[kmeans.labels_ == i]#第i个类中的所有点 #绘制散点图 plt.scatter(cluster_data[:, 0],#x坐标 cluster_data[:, 1],#y坐标 c=colors[i], #颜色 marker=markers[i], #形状 s=100,#点的大小 edgecolor=\'black\',#边缘颜色 label=f\'类 {i + 1}\'#图例 )#绘制类中心plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, marker=\'*\', c=\'yellow\', edgecolor=\'black\', label=\'类中心\')#添加标签for i, point in enumerate(data):#遍历每一行，即所有点 plt.text(point[0] + 0.05,#标签偏移 -> 不直接覆盖在点上 point[1] + 0.05, f\'({point[0]},{point[1]})\',#标签 fontsize=9)#字体大小#信息plt.title(\'K-Means聚类结果\')plt.xlabel(\'X轴\')plt.ylabel(\'Y轴\')plt.grid(True, linestyle=\'--\', alpha=0.7)plt.legend()plt.axis([-1, 6, -1, 5]) # 设置坐标轴范围#2.绘制决策边界的图像plt.subplot(2, 2, 2)#创建网格点x_min, x_max = -1, 6y_min, y_max = -1, 5xx, yy = np.meshgrid(#将两个一维数组转化为网格 -> xx和yy为网格所有点的x和y坐标的60*70矩阵 np.arange(x_min, x_max, 0.1),#生成范围上步长为0.1的一维数组 -> 70个点 np.arange(y_min, y_max, 0.1)#60个点)#预测网格点的簇标签#ravel()将矩阵展平为一维数组 -> 60*70=4200个元素#np.c_[]将两个一维数组合并为4200*2的矩阵Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])#预测每个网格点所属的类Z = Z.reshape(xx.shape)#变回60*70网格#绘制决策区域cmap_light = ListedColormap([\'#FFAAAA\', \'#AAAAFF\'])#创建背景颜色plt.contourf(xx, yy, Z, alpha=0.3, cmap=cmap_light)#根据所属类填充颜色#绘制数据点和类中心for i in range(2): cluster_data = data[kmeans.labels_ == i] plt.scatter(cluster_data[:, 0], cluster_data[:, 1], c=colors[i], marker=markers[i], s=100, edgecolor=\'black\', label=f\'类 {i + 1}\')plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, marker=\'*\', c=\'yellow\', edgecolor=\'black\', label=\'类中心\')#绘制决策边界plt.contour(xx, yy, Z, levels=[0.5],#在0和1两类间绘制边界 linewidths=2, colors=\'green\')plt.title(\'决策边界\')plt.xlabel(\'X轴\')plt.ylabel(\'Y轴\')plt.grid(True, linestyle=\'--\', alpha=0.7)plt.legend()#3.绘制新数据点预测plt.subplot(2, 2, 3)#新数据点new_points = np.array([[0, 0], [4, 4]])new_labels = kmeans.predict(new_points)#所属的类#绘制原始数据点for i in range(2): cluster_data = data[kmeans.labels_ == i] plt.scatter(cluster_data[:, 0], cluster_data[:, 1], c=colors[i], marker=markers[i], s=100, edgecolor=\'black\', alpha=0.5)#绘制类中心plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, marker=\'*\', c=\'yellow\', edgecolor=\'black\', alpha=0.5)#绘制预测数据点for i, point in enumerate(new_points): plt.scatter(point[0], point[1], c=colors[new_labels[i]], marker=\'D\', s=150, edgecolor=\'black\', label=f\'新点{chr(65 + i)}\') plt.text(point[0] + 0.05, point[1] + 0.05, f\'新点{chr(65 + i)}:({point[0]},{point[1]})\',#chr()转字符 -> 大写字母 fontsize=9)plt.title(\'新数据点预测\')plt.xlabel(\'X轴\')plt.ylabel(\'Y轴\')plt.grid(True, linestyle=\'--\', alpha=0.7)plt.legend()plt.axis([-1, 6, -1, 5])#调整布局并显示plt.tight_layout(pad=3.0)#增加子图间距plt.show()

真的复杂……

注意其中决策边界生成的原理是将表格细分成多个单点，然后求出所有单点的所属类填充背景颜色。

八、数据包络分析（DEA）

阴间玩意……

1.适用场景

数据包络分析是一种评价多投入和多产出问题中效率的方法。这里，效率简单来说就是产出和投入的比率。数据包络分析本质上就是通过这个比率来生成权重。

2.基本概念

首先，需要了解决策单元（DMU）的含义。决策单元是指相同类型的企业或同一企业的不同时期等通过一定数量的投入获得一定数量的产出。举个例子，现在有中科大，合工大和安大的科研投入，教育投入，建设投入以及科研成果产出和优秀学生产出这五个指标，那么这三所学校就是三个决策单元。之后，还需要区分投入指标和产出指标。那么在上述例子中前三个就是投入指标，后两个就是产出指标。数据包络分析就是在评价各决策单元的相对效率性。

所以，数据包络分析又分为以投入为导向的CCR和以产出为导向的BCC。CCR就是假设产出效率不变，即投入增加的比例会导致产出同比例增加，目标是投入和产出的比例尽可能大，所以这本质上就是在求解一个非线性规划的问题。BCC是对CCR的改进，是假设的投入增加的比例不一定导致产出同比例增加，更符合实际情况。要求的是在相同投入下，产出更多的资源，对应回现实就是生产技术的效率。

3.CCR模型

假设投入指标为X，产出指标为Y，那其目标函数的表达式为：，其中u和v分别为产出和投入的权重向量，那么约束条件就是，即投入和产出比不可能超过百分百。

虽然这是一个非线性规划，但其实可以转化成线性规划：

其中，lambda_i为第i个决策变量的权重，Xij为第i个决策变量第j个投入，Yij为第i个决策变量第j个产出。theta为效率得分，取值为0到1，意义是输入资源的最小压缩比例。举个例子，若theta为0.8，那么意思就是该决策单元的投入缩减到原来的80%后仍可保持当前的产出水平，那么目前的投入就有20%的浪费。之后，Xkj表示当前正在计算的第k个决策单元的第j个投入，即计算该决策变量相对其他决策单元的相对效率，那么此时就是计算该决策单元的效率得分。

在不同的生产规模下，规模报酬也会随之改变。生产规模小时，投入产出比会随着规模的增加而迅速提升，称为规模报酬递增。当生产达到高峰期时，产出与规模成正比而达到最适生产规模，称为规模报酬固定。当生产规模过于巨大时，产出会有所减缓，此时称为规模报酬递减，也就是投入增加时，产出增加的比例会少于投入增加的比例。

解释一下规模报酬的现实意义。假设规模报酬不变（CRS），就是投入和产出成比例，符合理想情况，即总能达到最优规模。而假设规模报酬可变（VRS），那就是投入和产出不成比例，承认除了生产规模，生产效率还由比如管理能力等限制。

CCR模型就是假设规模报酬不变，所以其通过lambda构建了虚拟的决策单元，使其达到最优规模。那么lambda就包含了第i个决策单元的规模报酬信息，可以通过放缩反应现实情况和理想情况的差距。当lambda的和为1的时候规模报酬固定，大于1则递减，小于1则递增。

4.BCC模型

BCC模型就是假设规模报酬可变，在CCR的基础上增加了lambda的和等于1的约束。意义就是保证不会有lambda通过放缩来通过调整规模达到最优。那此时就代表着纯技术效率，剔除了生产规模对效率的影响。

这时就可以提出规模效率的概念。规模效率就等于CCR的效率得分比上BCC的效率得分。当规模效率等于1时，说明处于最优规模。若小于1就说明存在规模损失，此时就需要考察lambda之和来判断规模报酬是递增还是递减，然后决策时扩大规模还是减小规模。若BCC模型的效率得分小于1，那么说明此时是管理不佳导致的效率低下。

所以CCR模型反应的是理想情况下能达到多高效，而BCC模型反应的就是现实中能改进多少。

5.例题

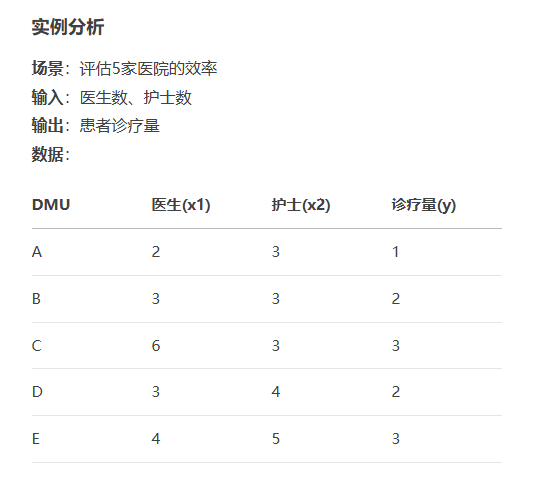
在这个例子中，决策单元就是五个医院，投入为医生和护士数，产出为治疗量。

import numpy as npfrom scipy.optimize import linprog# 输入输出数据 -> [医生, 护士, 诊疗量]data = np.array([ [2, 3, 1], # A [3, 3, 2], # B [6, 3, 3], # C [3, 4, 2], # D [4, 5, 3] # E])#CCR模型#dmu_index -> 当前评估的决策单元下标def dea_ccr(dmu_index, data): #决策单元数和指标数 n_dmu, n_var = data.shape #前两列 -> 投入 inputs = data[:, :2] #最后一列 -> 产出 outputs = data[:, 2] #目标函数系数 -> 只要得分效率theta，不要权重lambda c = [1] + [0] * n_dmu #投入约束 A_ub_inputs = [ #得分效率theta乘Xkj移到不等式左侧变负号 #a[i,j] -> a[i][j] #当前评估的决策变量的第i个投入 [-inputs[dmu_index, i]] + [inputs[j, i] for j in range(n_dmu)]#每个决策单元 for i in range(inputs.shape[1])#两个投入指标 ] #输出约束 #左右添负号 A_ub_outputs = [ [0] + [-outputs[j] for j in range(n_dmu)]#每个决策单元 ] b_ub_outputs = [-outputs[dmu_index]] A_ub = A_ub_inputs + A_ub_outputs b_ub = [0] * len(A_ub_inputs) + b_ub_outputs #变量边界 -> theta无界，lambda大于等于0 bounds = [(None, None)] + [(0, None)] * n_dmu # 求解线性规划 res = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds) return res.x[0],sum(res.x[1:])#BCC模型def dea_bcc(dmu_index, data): n_dmu, n_var = data.shape inputs = data[:, :2] outputs = data[:, 2] c = [1] + [0] * n_dmu #输入约束 A_ub_inputs = [ [-inputs[dmu_index, i]] + [inputs[j, i] for j in range(n_dmu)] for i in range(inputs.shape[1]) ] #输出约束 A_ub_outputs = [ [0] + [-outputs[j] for j in range(n_dmu)] ] b_ub_outputs = [-outputs[dmu_index]] #增加lambda的等式约束 A_eq = [[0] + [1] * n_dmu] b_eq = [1] A_ub = A_ub_inputs + A_ub_outputs b_ub = [0] * len(A_ub_inputs) + b_ub_outputs bounds = [(None, None)] + [(0, None)] * n_dmu res = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds) return res.x[0]# 计算所有决策单元效率print(\"决策单元 | CCR效率 | BCC效率 | 规模效率 | lambda之和\")for i, dmu in enumerate([\'A\', \'B\', \'C\', \'D\', \'E\']): ccr_eff,sum_lambda_ccr = dea_ccr(i, data)#CCR的得分效率 bcc_eff = dea_bcc(i, data)#BCC的得分效率 scale_eff = ccr_eff / bcc_eff #规模效率 print(f\"{dmu} | {ccr_eff:.4f} | {bcc_eff:.4f} | {scale_eff:.4f} | {sum_lambda_ccr:.4f}\")

CCR模型首先就是把投入和产出抓出来，然后变量向量第一个是theta，后面是lambda。因为目标函数只要theta，所以目标函数的系数矩阵就是只要一个theta，后面的lambda都不要。

之后是投入约束条件的系数矩阵，考虑把右侧部分添负号移到左侧，那么就是当前评价的决策单元的每个投入，再加上每个决策单元的每个投入。

之后是输出约束条件的系数矩阵因为是大于等于的形式，所以要先左右添负号转成小于等于的形式。然后因为没有theta部分，所以上来先是一个0，之后是每个决策单元的产出。

最后把两个约束条件合并，求解线性规划并返回theta即可。

BCC模型就是加上了lambda的等式约束。

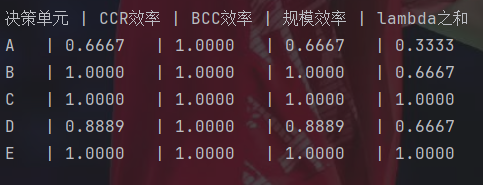
重点是给出数据现实层面的解释。

医院B，C和E的CCR和BCC得分效率均为1，规模效率也为1，说明纯技术达到最优，且综合效率也达到最优。但注意到医院B的lambda之和小于1，说明虽然医院B当前已经达到了效率最优，但通过加大投入仍然可以使产出得到增大。

医院A的BCC效率为1，说明此时纯技术达到最优，那么就不是管理效率导致的效率不足。而CCR效率小于1，那么说明存在投入资源浪费的情况。而规模效率小于1，说明此时规模上存在问题。又因为其lambda之和小于1，所以这是因为规模不足而导致超额投入。医院D和医院A类似，但情况会好上一些。

总结

之后如果时间来得及的话我会考虑把每个算法封装成函数，到时候可能会考虑在这里和github上分享资源，前提是来得及……以前只学算竞感觉还能忙得过来，现在加上建模明显感觉到力不从心了……

END