C++：二叉树进阶算法OJ题__详细讲解附有参考代码（根据二叉树创建字符串、二叉树的最近公共祖先、将二叉搜索树转化为排序的双向链表、从前序与中序遍历序列构造二叉树、二叉树的前序&中序&后序非递归遍历）

目录

1.根据二叉树创建字符串

题目描述

解题思路

参考答案

2.二叉树的最近公共祖先

题目描述

思路一

解题思路

参考答案

思路二

解题思路

参考答案

3.将二叉搜索树转化为排序的双向链表

题目描述

解题思路

参考答案

4.从前序与中序遍历序列构造二叉树

题目描述

解题思路

参考答案

5.二叉树的前序非递归遍历

题目描述

解题思路

参考答案

6.二叉树的中序非递归遍历

题目描述

解题思路

参考答案

7.二叉树的后序非递归遍历

题目描述

解题思路

参考答案

1.根据二叉树创建字符串

根据二叉树创建字符串https://leetcode.cn/problems/construct-string-from-binary-tree/

题目描述

给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。

空节点使用一对空括号对 \"()\" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

示例 1：

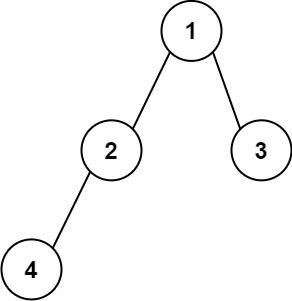
输入：root = [1,2,3,4]输出：\"1(2(4))(3)\"解释：初步转化后得到 \"1(2(4)())(3()())\" ，但省略所有不必要的空括号对后，字符串应该是\"1(2(4))(3)\" 。

示例 2：

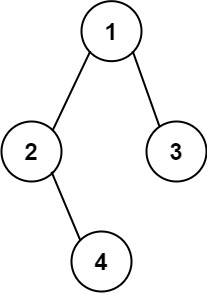
输入：root = [1,2,3,null,4]输出：\"1(2()(4))(3)\"解释：和第一个示例类似，但是无法省略第一个空括号对，否则会破坏输入与输出一一映射的关系。

解题思路

•     前序遍历的话直接使用就可以解决， 这道题难在括号的添加。
•     添加的括号的逻辑是将左子树和右子树的数据分别用括号括起来，当没有左节点或者右节点的时候，括号可以省略。但是当左节点为空且右节点不为空时，空括号不能省略。
•     根据这个逻辑，我们可以将其转化为：当左节点不为空或者右节点不为空时，在字符串后加上\'(\' + 左节点数据 + \')\';当右节点不为空时，在字符串后加上\'(\' + 右节点数据 + \')\'

参考答案

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ /* 前序遍历的话直接使用就可以解决， 这道题难在括号的添加。 添加的括号的逻辑是将左子树和右子树的数据分别用括号括起来，当没有左节点或者右节点的时候，括号可以省略。但是当左节点为空且右节点不为空时，空括号不能省略。 根据这个逻辑，我们可以将其转化为：当左节点不为空或者右节点不为空时，在字符串后加上\'(\' + 左节点数据 + \')\';当右节点不为空时，在字符串后加上\'(\' + 右节点数据 + \')\'*/class Solution {public: string tree2str(TreeNode* root) { string str; if (root == nullptr) { return str; } str += to_string(root->val); if (root->left != nullptr || root->right != nullptr) { str += \'(\'; str += tree2str(root->left); str += \')\'; } if (root->right != nullptr) { str += \'(\'; str += tree2str(root->right); str += \')\'; } return str; }};

2.二叉树的最近公共祖先

二叉树的最近公共祖先https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

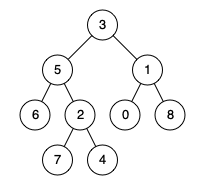
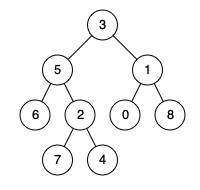
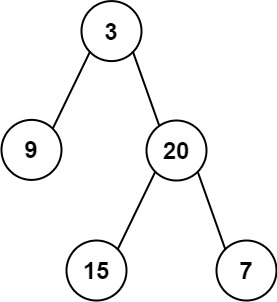
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1输出：3解释：节点5和节点1的最近公共祖先是节点3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4输出：5解释：节点5和节点4的最近公共祖先是节点5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2输出：1

提示：

• 树中节点数目在范围 [2, 105] 内。
• -109 <= Node.val <= 109
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中。

思路一

解题思路

    两个节点的最近公共祖先有一个特征：两个节点分别在最近公共祖先的左子树和右子树中。其中有一种特殊情况，那就是最近公共祖先刚好就是其中一个节点。

    通过这个思路，我们可以分别判断每个节点是否在某个节点的左子树和右子树，然后再通过判断两个节点是否分别在同一个节点的左子树和右子树，若是，则这个节点就是两个节点的最近公共祖先。

    想要实现这个思路，我们需要一个判断某节点是否在某个头结点所在的树中，这个可以借助递归的方法实现

参考答案

该方法虽能解决问题，但是时间复杂度过高，为O(N)，不推荐使用此方法

class Solution {public: bool IsInTree(TreeNode* root, TreeNode* p) { if (root == nullptr) { return false; } return root == p || IsInTree(root->left, p) || IsInTree(root->right, p); } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if (root == nullptr) { return nullptr; } if (root == p || root == q) { return root; } bool pInLeft = IsInTree(root->left, p); bool pInRight = !pInLeft; bool qInLeft = IsInTree(root->left, q); bool qInRight = !qInLeft; if (pInLeft && qInLeft) { return lowestCommonAncestor(root->left, p, q); } else if (pInRight && qInRight) { return lowestCommonAncestor(root->right, p, q); } else { return root; } }};

思路二

解题思路

    思路二：

    既然是要找最近公共祖先，那就不妨将从根节点到两个节点的路径记录下来，然后倒着寻找第一个相交的位置，此位置即为最近公共祖先。

    要实现记录路径和倒着寻找，我们可以借助“栈”先进后出的性质。

    记录路径时，先入根节点，然后依次入左节点和右节点（前序遍历），如果一个节点的左子树和右子树中均没有两个节点，则从栈中删除该节点。

    倒着寻找时，我们可以类比链表找第一个公共节点的方法，先让长的先走，即先让数据较多的栈逐个删除数据，直到两个栈一样大。然后两个栈同时删除数据，直到两个栈的第一个元素相同时，该元素即为最近公共祖先。

参考答案

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; *//* 思路二： 既然是要找最近公共祖先，那就不妨将从根节点到两个节点的路径记录下来，然后倒着寻找第一个相交的位置，此位置即为最近公共祖先。 要实现记录路径和倒着寻找，我们可以借助“栈”先进后出的性质。 记录路径时，先入根节点，然后依次入左节点和右节点（前序遍历），如果一个节点的左子树和右子树中均没有两个节点，则从栈中删除该节点。 倒着寻找时，我们可以类比链表找第一个公共节点的方法，先让长的先走，即先让数据较多的栈逐个删除数据，直到两个栈一样大。然后两个栈同时删除数据，直到两个栈的第一个元素相同时，该元素即为最近公共祖先。*/class Solution {public: bool GetPath(stack& s, TreeNode* root, TreeNode* p) { if (root == nullptr) { return false; } s.push(root); if (root == p) { return true; } if (GetPath(s, root->left, p)) { return true; } if (GetPath(s, root->right, p)) { return true; } s.pop(); return false; } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if (root == nullptr) { return nullptr; } stack s1, s2; GetPath(s1, root, p); GetPath(s2, root, q); while (s1.size() != s2.size()) { if (s1.size() > s2.size()) { s1.pop(); } else { s2.pop(); } } while (s1.top() != s2.top()) { s1.pop(); s2.pop(); } return s1.top(); }};

3.将二叉搜索树转化为排序的双向链表

将二叉搜索树转化为排序的双向链表https://leetcode.cn/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/

题目描述

将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

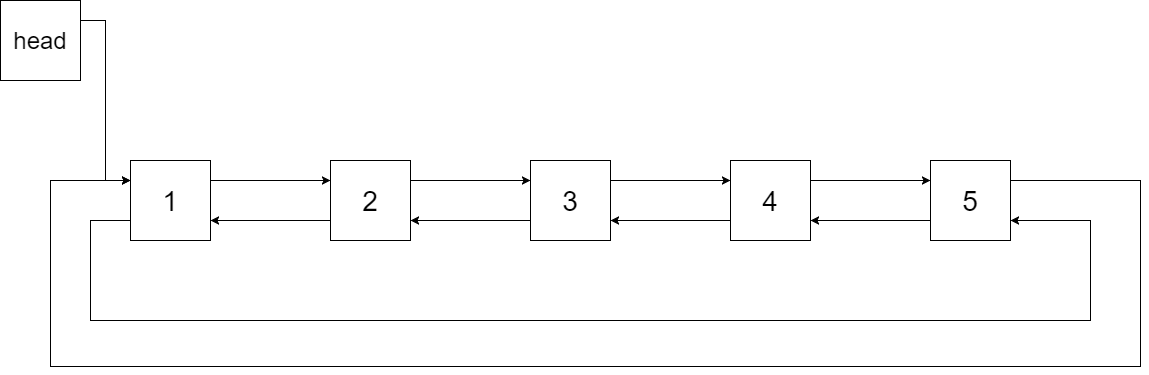
对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

特别地，我们希望可以 就地 完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。

示例 1：

输入：root = [4,2,5,1,3] 

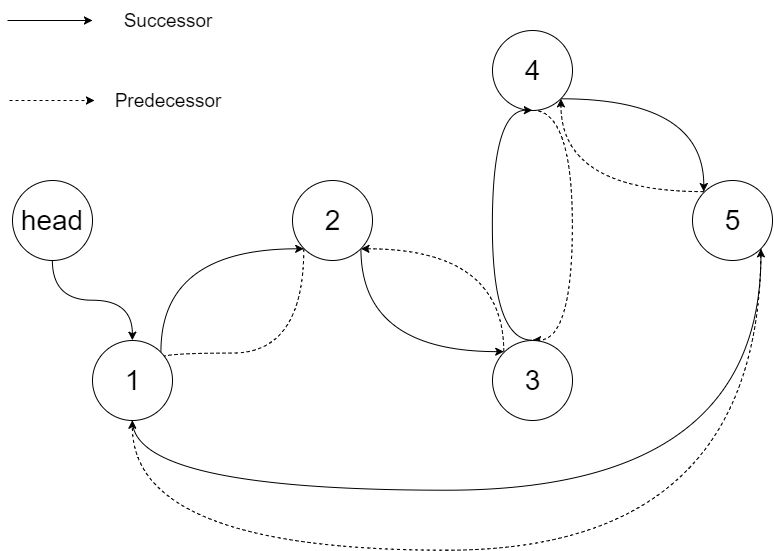
输出：[1,2,3,4,5]解释：下图显示了转化后的二叉搜索树，实线表示后继关系，虚线表示前驱关系。

示例 2：

输入：root = [2,1,3]输出：[1,2,3]

示例 3：

输入：root = []输出：[]解释：输入是空树，所以输出也是空链表。

示例 4：

输入：root = [1]输出：[1]

提示：

• -1000 <= Node.val <= 1000
• Node.left.val < Node.val < Node.right.val
• Node.val 的所有值都是独一无二的
• 0 <= Number of Nodes <= 2000

解题思路

    题目中给出提示“对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点”。

    我们可以根据这个提示通过中序遍历来遍历搜索二叉树，这样遍历的过程就是有序的，在这个过程中记录当前节点和上一个节点，将二者互相连接起来，这样除了首尾没有连接以外剩下的节点都互相连接起来了。最后找到头结点和尾节点，将二者连接起来就完成了。

参考答案

class Solution {public: void InOrderConvert(Node* cur, Node*& prev, Node*& head) { if (cur == nullptr) { return; } InOrderConvert(cur->left, prev, head); if (prev == nullptr) { prev = cur; head = cur; } else { prev->right = cur; cur->left = prev; prev = cur; } InOrderConvert(cur->right, prev, head); return; } Node* treeToDoublyList(Node* root) { if (root == nullptr) { return nullptr; } Node* prev = nullptr; Node* cur = root; Node* head = nullptr; InOrderConvert(root, prev, head); head->left = prev; prev->right = head; return head; }};

4.从前序与中序遍历序列构造二叉树

从前序与中序遍历序列构造二叉树https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

解题思路

•     只有前序遍历或者中序遍历或者后序遍历不能确定唯一的二叉树，但是若知道其中两个就可确定，比如在此题中要求从前序与中序遍历序列构造二叉树。
•     前序遍历的顺序是根-左子树-右子树，中序遍历的顺序是左子树-根-右子树，所以此题的思路为：前序确定根，中序分割左子树和右子树。
•     整体采用递归的思想，依次取前序遍历的每个值，这个值就是头结点，在中序遍历中根据这个头结点分割左子树和右子树，循环这个过程。

参考答案

class Solution {public: TreeNode* buildTree(vector& preorder, vector& inorder, int& prei, int inbegin, int inend) { if (inbegin > inend) { return nullptr; } TreeNode* t = new TreeNode(preorder[prei]); int find = inbegin; while (inorder[find] != preorder[prei]) { find++; } prei++; t->left = buildTree(preorder, inorder, prei, inbegin, find - 1); t->right = buildTree(preorder, inorder, prei, find + 1, inend); return t; } TreeNode* buildTree(vector& preorder, vector& inorder) { int prei = 0; int inbegin = 0; int inend = inorder.size() - 1; return buildTree(preorder, inorder, prei, inbegin, inend); }};

5.二叉树的前序非递归遍历

二叉树的前序非递归遍历https://leetcode.cn/problems/binary-tree-preorder-traversal/

题目描述

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

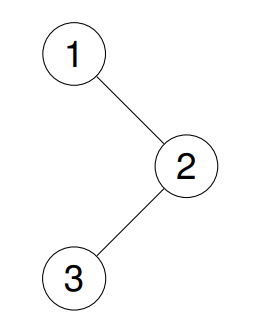
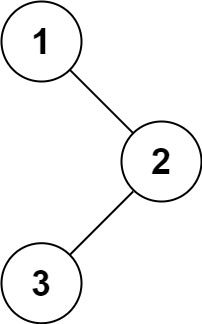
输入：root = [1,null,2,3]

输出：[1,2,3]

解释：

示例 2：

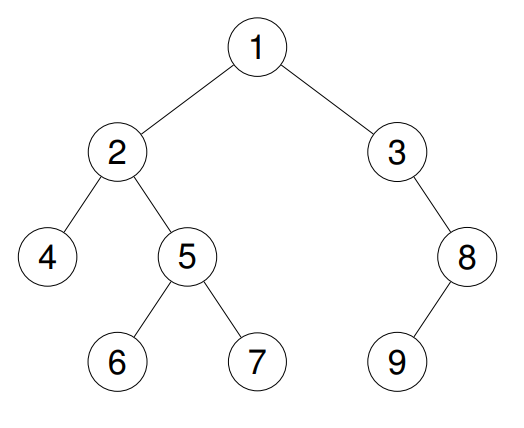
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[1,2,4,5,6,7,3,8,9]

解释：

示例 3：

输入：root = []

输出：[]

示例 4：

输入：root = [1]

输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

解题思路

•     这道题用递归较为简单，但是递归要建立栈帧，不但消耗时间较长，而且栈的空间较小，远比堆的空间要小得多，所以递归深度较大时容易出现栈溢出的情况，所以我们要考虑如何把递归转化为非递归。一般递归转化为非递归有两种方法：要么考虑用循环来实现，如果循环不容易实现，可以借助栈和队列来模拟建立栈帧和入数据、出数据的过程，进而实现非递归。
•     在这道题中，我们可以借助栈来模拟建立栈帧的过程。将根节点和左节点依次放入数组和栈中，再依次取出栈顶数据，将栈顶元素的右节点放入数组和栈中，不断循环这个过程，就可以实现非递归前序遍历。

参考答案

class Solution {public: vector preorderTraversal(TreeNode* root) { vector v; if (root == nullptr) { return v; } stack st; TreeNode* cur = root; while (cur || !st.empty()) { while (cur) { v.push_back(cur->val); st.push(cur); cur = cur->left; } TreeNode* top = st.top(); st.pop(); cur = top->right; } return v; }};

6.二叉树的中序非递归遍历

二叉树的中序非递归遍历https://leetcode.cn/problems/binary-tree-inorder-traversal/

题目描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

输入：root = [1,null,2,3]输出：[1,3,2]

示例 2：

输入：root = []输出：[]

示例 3：

输入：root = [1]输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

解题思路

•         这道题的思想和前序非递归遍历及其类似，只需对实现的方式稍微修改一下就行了。

参考答案

class Solution {public: vector inorderTraversal(TreeNode* root) { vector v; if (root == nullptr) { return v; } stack st; TreeNode* cur = root; while (cur || !st.empty()) { while (cur) { st.push(cur); cur = cur->left; } TreeNode* top = st.top(); v.push_back(top->val); st.pop(); cur = top->right; } return v; }};

7.二叉树的后序非递归遍历

二叉树的后序非递归遍历https://leetcode.cn/problems/binary-tree-postorder-traversal/

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

输入：root = [1,null,2,3]

输出：[3,2,1]

解释：

示例 2：

输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[4,6,7,5,2,9,8,3,1]

解释：

示例 3：

输入：root = []

输出：[]

示例 4：

输入：root = [1]

输出：[1]

提示：

• 树中节点的数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

解题思路

•     相较于前序和中序，后序非递归遍历较为复杂，套用前面解决前序非递归遍历和中序非递归遍历的方法我们可以先不将栈顶元素删除，直接将栈顶元素的右节点加入到栈中，等到第二次该元素成为栈顶元素的时候再将其加到数组中并从栈中删除。但是这个过程中会出现一个问题：如何判断栈顶元素是第一次访问还是第二次访问？换个说法，也就是说我如何确定取出的栈顶元素是直接放入数组还是先去访问该元素的右子树？
•     从后序遍历的过程思考，得出以下三个规律：（1）当左节点入数组时，整个左子树都已经遍历完成了 （2）当右节点不为空且右子树已全部访问时，上一个入数组的是右子树的根 （3）当右节点不为空且右子树还没有访问时，上一个入数组的是左子树的根
•     根据这个规律，我们可以记录上一个入数组的节点，由此判断判断栈顶元素是第一次访问还是第二次访问。

参考答案

class Solution {public: vector postorderTraversal(TreeNode* root) { vector v; if (root == nullptr) { return v; } stack st; TreeNode* cur = root; TreeNode* prev = nullptr; while (cur || !st.empty()) { while (cur) { st.push(cur); cur = cur->left; } TreeNode* top = st.top(); if (top->right) { if (prev == top->right) {  v.push_back(top->val);  st.pop();  prev = top; } else {  cur = top->right; } } else { v.push_back(top->val); st.pop(); prev = top; } } return v; }};

男装品牌