回溯、递推、递归、分治和动态规划
递归
函数出现调用自身的代码块就是递归,它是一种编程的实现方式
int maxDepth(TreeNode* root) { if(root==NULL) return 0; int l_depth=maxDepth(root->left); int r_depth=maxDepth(root->right); return max(l_depth,r_depth)+1; }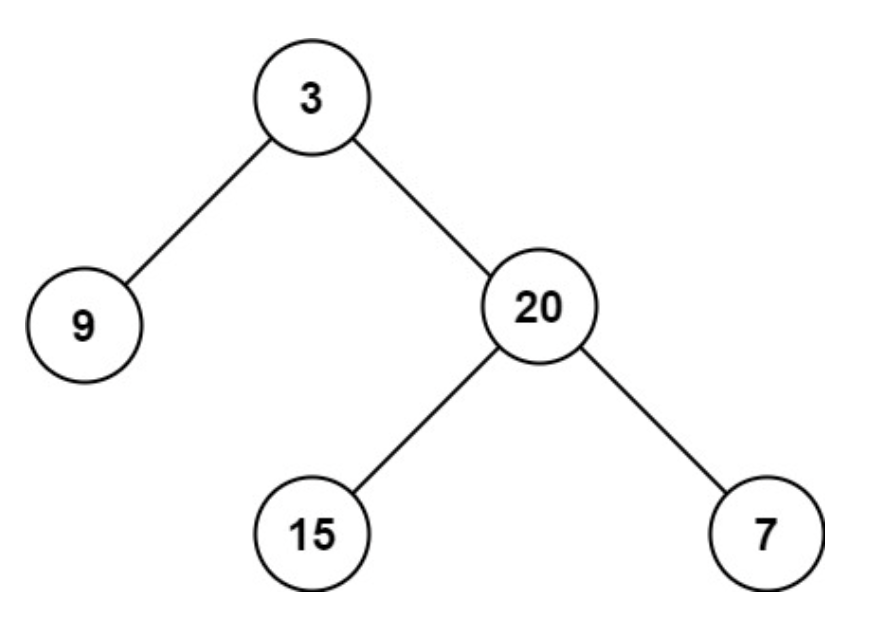
->int maxDepth(3) 最终返回3
->if(root==0) 3!=0
->int l_depth=maxDepth(3->left=9) 最终maxDepth(3->left=9)的返回值为1,赋值给l_depth
->if(root==0) 9!=0
->int l_depth=maxDepth(9->left=NULL) 局部变量,也就是副本,l_depth=0
->if(root==0)NULL==NULL return 0 //int l_depth = maxDepth(9->left=NULL) 回溯值为0
->int r_depth = maxDepth(9->right=NULL) 局部变量,也就是副本,l_depth=0
->if(root==0)NULL==NULL return 0 //int r_depth = maxDepth(9->right=NULL) 回溯值为0
return max(0,0)+1 //int l_depth=maxDepth(9)的回溯值为1
->int r_depth=maxDepth(3->right=20) 最终返回2赋值给r_depth
->if(root==0)? 20!=0
->int l_depth=maxDepth(20->left=15)最终返回1赋值给l_depth
->if(15==0)?不等于
->int l_depth=maxDepth(15->left=NULL) 最终返回0赋值给l_depth
->if(NULL==0) return 0;
->int r_depth = maxDepth(15->right=NULL) 最终返回0赋值给r_depth
->if(NULL==0) return 0;
-> return max(0,0)+1 //int l_depth=maxDepth(15)的回溯值为1
->int r_depth=maxDepth(20->right=7)最终返回1赋值给r_depth
->if(7==0)?不等于,继续执行下一步
->int l_depth=maxDepth(7->left=NULL) 最终返回0赋值给l_depth
->if(NULL==0) return 0;
->int r_depth = maxDepth(7->right=NULL) 最终返回0赋值给r_depth
->if(NULL==0) return 0;
-> return max(0,0)+1 //int l_depth=maxDepth(20)的回溯值为2
->return max(1,1)+1 //int r_depth=maxDepth(7)的回溯值为1
->retun max(1,2)+1 //int r_depth=maxDepth(3)的回溯值为2+1=3
平时该咋思考呢,看原问题与子问题关系的那个return 语句,比如
int factorial(int n){if(n<=0) return 1;return n*factrial(n-1);} 先跳到base case ,factorial(0),那么上一步就是1*factorial(0)即,1*1,从右往前看
回溯算法
回溯算法的核心是枚举所有可能解并筛选有效解
-
排列问题(Permutations)
要求生成集合中元素的所有可能排列(考虑顺序)。-
例:
[1,2,3]的全排列为[[1,2,3], [1,3,2], [2,1,3], ...]。 -
核心逻辑:每个位置尝试未使用的元素,使用后标记,回溯时撤销标记。
-
-
组合问题(Combinations)
要求生成集合中元素的所有可能组合(不考虑顺序)。-
例:
[1,2,3]中选 2 个元素的组合为[[1,2], [1,3], [2,3]]。 -
核心逻辑:通过 “起点索引” 避免重复(如选过 1 后,只从 2、3 开始选)。
-
-
子集问题(Subsets)
要求生成集合的所有可能子集(包括空集和全集)。-
例:
[1,2]的子集为[[], [1], [2], [1,2]]。 -
核心逻辑:每个元素可 “选” 或 “不选”,通过递归分支实现两种选择,回溯时无需撤销(因子集是逐步累积的)。
-
-
约束满足问题(Constraint Satisfaction Problems)
要求在满足特定约束条件下寻找解,如:-
数独:每行、每列、每个 3×3 宫内数字不重复。
-
N 皇后:皇后之间不能同行、同列、同对角线。
-
核心逻辑:通过剪枝(提前排除违反约束的路径)减少无效搜索。
-
-
路径搜索问题
如在网格中寻找从起点到终点的所有路径(可带障碍),或迷宫求解。-
核心逻辑:记录当前路径,遇到死胡同则回退,尝试其他方向。
-
基础回溯算法可能因枚举过多而效率低下,实际应用中常结合以下优化方式,形成 “变体”:
-
带剪枝的回溯
最常用的优化方式:在递归探索时,提前判断当前路径是否可能产生有效解,若不可能则直接终止该分支(“剪枝”),避免无效递归。-
例:N 皇后问题中,若当前行的某一列已被上方皇后攻击,则无需继续递归该行后续列。
-
-
记忆化回溯(回溯 + 缓存)
对重复出现的子问题,记录其结果(缓存),避免重复计算。-
例:在某些复杂的组合问题中,若不同分支会遇到相同的 “剩余元素 + 约束条件”,可缓存该状态的解。
-
-
迭代式回溯(非递归回溯)
回溯通常用递归实现,但也可通过栈模拟递归过程(手动维护调用栈和状态),避免递归深度过大导致的栈溢出。-
本质与递归回溯一致,只是实现方式从 “函数调用” 改为 “栈操作”。
-
-
分支限界回溯
在优化问题(如求最优解)中,为每个分支设定 “下界” 或 “上界”,若当前分支的最优可能已差于已知最优解,则剪枝。-
例:旅行商问题(TSP)中,若当前路径长度已超过已知最短路径,则终止该分支。
-


