字典树详解

字典树（Trie）， 是一种专门用于高效存储和检索字符串集合的树形数据结构。

字典树核心思想是利用将字符串的公共前缀来节省时间和空间。

假设我们现在有一个字符串集合 $S$：

s = { abc abs xyz xy s=\\begin{cases} \\texttt{abc}\\\\ \\texttt{abs}\\\\ \\texttt{xyz}\\\\ \\texttt{xy}\\\\ \\end{cases} s=⎩ ⎨ ⎧​abcabsxyzxy​

则字典树的结构为：

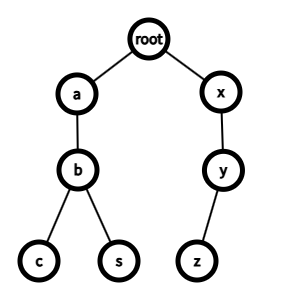
其中 $c,s,y,z$ 均为结束节点。

操作

1. Insert（插入）操作：

   遍历每个字符 $c$，若此前不存在 $c$，则创建 $c$。

   设 n o d e u , c node_{u,c} nodeu,c​ 表示节点 $u$ 的 $c$ 字符所指向的下一个节点。

   每次插入时需要在这个字符所代表的节点的出现次数 $+1$。

   若需要查询前缀数量，则直接返回末尾的 e x i s t uexist_u existu​ 数量。

   若统计完整字符，则需要将这个字符串的末尾节点的出现此时 $+1$。

   查询时只需要返回末尾的 e x i s t uexist_u existu​ 数量即可。

实现

void Insert(string s){ int u=0; for(auto z:s){ int c=check(z); if(!node[u][c]){ node[u][c]=++tmp; } u=node[u][c]; exist[u]++; } return;}

3. Search（查询）操作：

   遍历每个字符串 $c$，若 $c$ 不存在，则直接返回 $0$。

   若顺利遍历完成，则直接返回记录的末尾节点数量即可。

实现

int Search(string s){ int u=0; for(auto z:s){ int c=check(z); if(!node[u][c]){ return 0; } u=node[u][c]; } return exist[u];}

例题1：P8306 【模板】字典树

首先将所有模式串进行插入。

对于每次查询，直接返回 $\mathrm{Search}(s)$ 的结果即可。

实现

#includeusing namespace std;#define int long longint t,n,m,node[3000005][65],exist[3000005],tmp;int check(char x){if(x>=\'A\'&&x<=\'Z\'){return x-\'A\';}else if(x>=\'a\'&&x<=\'z\'){return x-\'a\'+26;}return x-\'0\'+52;}void Insert(string s){int u=0;for(auto z:s){int c=check(z);if(!node[u][c]){node[u][c]=++tmp;}u=node[u][c];exist[u]++;}return;}int Search(string s){int u=0;for(auto z:s){int c=check(z);if(!node[u][c]){return 0;}u=node[u][c];}return exist[u];}string s;signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);for(cin>>t;t;t--){cin>>n>>m;for(int i=0;i<=tmp;i++){exist[i]=0;for(int j=0;j<200;j++){node[i][j]=0;}}tmp=0;for(int i=1;i<=n;i++){cin>>s;Insert(s);}for(int i=1;i<=m;i++){cin>>s;cout<<Search(s)<<\'\\n\';}}return 0;}

例题2：UVA-10887 Concatenation of Languages

暴力匹配。

若 $s+s1$ 的组合之前并未出现过，则累加答案，并进行标记。

实现

#includeusing namespace std;#define int long longint t,tmp,Case,ans,n,m,node[400005][255],exist[400005];string s[1505],s1[1505];set<string>st;void Insert(string s){int u=0;for(auto z:s){if(!node[u][z]){node[u][z]=++tmp;}u=node[u][z];exist[u]++;}}int Search(string s){int u=0;for(auto z:s){if(!node[u][z]){return 0;}u=node[u][z];}return exist[u];}signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);for(cin>>t;t;t--){cin>>n>>m;//fill(node[0],node[(n+m)*10+1],0);//fill(exist,exist+(n+m)*10+1,0);tmp=ans=0,Case++;cin.get();st.clear();for(int i=1;i<=n;i++){getline(cin,s[i]);}for(int i=1;i<=m;i++){getline(cin,s1[i]);}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){//ans+=(!Search(s[i]+s1[j]));ans+=(!st.count(s[i]+s1[j]));st.insert(s[i]+s1[j]);}}cout<<\"Case \"<<Case<<\": \"<<ans<<\'\\n\';}return 0;}

例题3：HDU-2072 单词数

坑人。

每次先清空字典树，然后对于每个单词，先用字典树判断这个单词之前是否存在过。

若不存在，将 $s$ 插入字典树中，且累加答案。

注意细节！！！

实现

#includeusing namespace std;#define int long longint node[100005][29],ans,tmp,exist[100005];string s;int check(char x){if(x>=\'a\'&&x<=\'z\'){return x-\'a\';}return 28;}void Insert(string s){int u=0;for(auto z:s){if(!node[u][check(z)]){tmp++;node[u][check(z)]=++tmp;for(int i=0;i<29;i++){node[tmp][i]=0;}exist[tmp]=0;}u=node[u][check(z)];}exist[u]++;}int Search(string s){int u=0;for(auto z:s){if(!node[u][check(z)]){return 0;}u=node[u][check(z)];}return exist[u];}signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);while(true){for(int i=0;i<29;i++){node[0][i]=0;}tmp=ans=0;getline(cin,s);if(s==\"#\"){return 0;}string x=\"\";for(auto z:s){if(z!=\' \'){x+=z;}else if(x.size()){ans+=(!Search(x));Insert(x);x=\"\";}}if(x.size()){Insert(x);ans+=(Search(x)==1);}cout<<ans<<\'\\n\';}return 0;}