7.27 状态机dp|质数线性筛|序列化树
lc297 序列化树
序列化--bfs
cpp tip: string +=拼接,防mle
序列化和反序列化都采用层序遍历的方法,非常简单直观

tip

代码
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root)
{
if(root == nullptr) return \"\";
string res;
queue order;
order.push(root);
while (!order.empty())
{
int size = order.size();
while(size--)
{
auto top = order.front();
order.pop();
if(top == nullptr)
res+=\"null,\";
else
{
res+=to_string(top->val)+\",\";
order.push(top->left);
order.push(top->right);
}
}
}
res.erase(res.size()-1);
while (res.size()>=5&&res.substr(res.size()-5,5)==\",null\")
res.erase(res.size()-5,5);
return res;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
TreeNode* head = new TreeNode();
if(data.size() == 0)
return nullptr;
vector value;
int begin = 0 ,length = 0;
string value_part;
for(int i = 0;i<data.size();i++){
if(data[i] == \',\'){
value.push_back(data.substr(begin,length));
begin = i+1;
length = 0;
}
else
length++;
}
value.push_back(data.substr(begin,length));
head->val = stoi(value[0]);
queue tree;
tree.push(head);
int pos = 1;
while (pos<value.size()){
TreeNode *p = tree.front();
tree.pop();
if(value[pos]!=\"null\") {
p->left = new TreeNode(stoi(value[pos]));
tree.push(p->left);
}
pos++;
if(pos<value.size()&&value[pos]!=\"null\") {
p->right = new TreeNode(stoi(value[pos]));
tree.push(p->right);
}
pos++;
}
return head;
}
};
lc3628.状态机
六种状态变化,三种增加选择
1.设
long long l = 0, lc = 0, lct = 0, c = 0, ct = 0, lt = 0;
2.方程
if condition
status+=pre step
self++
3.返回值
return lct + max({ct, lc, lt});
进阶版见dp专栏[dp15] 两个字符串/二维dp

class Solution {
public:
long long numOfSubsequences(string s)
{
int t = ranges::count(s, \'T\');
long long l = 0, lc = 0, lct = 0, c = 0, ct = 0, lt = 0;
for (char b : s) {
if (b == \'L\')
{
l++;
}
else if (b == \'C\')
{
lc += l;
c++;
}
else if (b == \'T\') {
lct += lc;
ct += c;
t--;
}
lt = max(lt, l * t);
}
return lct + max({ct, lc, lt});
}
};
lc3629.质数传送--bfs+线性筛
1.预处理,挑出质因数--线性筛
2.建图
3.质数的倍数
tip: 相同数字的点,bfs到第一个时,就把全部的加入到队列中,之后就不用再次加入,.clear避免TLE
从数组第一个元素跳到最后一个元素的最少步数,跳的规则是:可以跳到相邻位置(前一个或后一个),或者跳到和当前元素有共同质因数的位置。
简单说下思路:
1. 先把数组里的元素按“质因数”分组,比如元素6(质因数2、3)会被分到2组和3组,这样能快速找到有共同质因数的位置。
2. 用队列和距离数组(dis)做“广度优先搜索”(类似一层层扩散找最短路径):
- 从起点(位置0)开始,记录到每个位置的最少步数。
- 每次从队列里取一个位置,看看它能跳到哪些地方(相邻位置、同组质因数的位置)。
- 只要找到到终点的步数,就是最少的(因为广度优先搜索先找到的一定是最短路径)。
这样就能高效算出最少跳几步到终点啦。
const int MX = 1\'000\'001;
vector prime_factors[MX];
int init = [] {
for (int i = 2; i < MX; i++) {
if (prime_factors[i].empty()) {
for (int j = i; j < MX; j += i) {
prime_factors[j].push_back(i);
}
}
}
return 0;
}();
class Solution {
public:
int minJumps(vector& nums) {
int n = nums.size();
unordered_map<int, vector> groups;
for (int i = 0; i < n; i++) {
for (int p : prime_factors[nums[i]]) {
groups[p].push_back(i);
}
}
int ans = 0;
vector vis(n, false);
queue q;
q.push(0);
vis[0] = true;
while (!q.empty()) {
int qSize = q.size();
for (int k = 0; k < qSize; k++) {
int i = q.front();
q.pop();
if (i == n - 1) return ans;
auto& idx = groups[nums[i]];
idx.push_back(i + 1);
if (i > 0) idx.push_back(i - 1);
for (int j : idx) {
if (!vis[j]) {
vis[j] = true;
q.push(j);
}
}
idx.clear();
}
ans++;
}
return -1;
}
};

一、线性筛(欧拉筛)与埃氏筛(埃拉托斯特尼筛法)
1. 埃氏筛(基础版)
- 思路:像“筛子”一样,从 2 开始,把每个质数的倍数(比如 2 的倍数、3 的倍数…)标记为合数,剩下没被标记的就是质数。
- 缺点:一个合数会被多个质数重复标记(比如 12,会被 2 和 3 分别标记),效率稍低。
2. 线性筛(欧拉筛,优化版)
- 思路:保证每个合数只被“最小质因数”筛掉,避免重复标记,时间复杂度是真正的 O(n)(线性),所以叫“线性筛”。
- 核心逻辑:
用 prime 数组存已找到的质数,遍历数 i 时,用 i 乘以 prime 里的质数,标记 i*prime[j] 为合数;
一旦 i 能被 prime[j] 整除,就停止,保证每个合数只被最小质因数筛掉。
二、(线性筛实现)
下面是对应 C++ 代码,功能是筛出 [2, maxValue] 内所有质数(习惯上质数定义从 2 开始,代码里做了调整):
const int maxValue = 1e6; // 定义筛法范围,可根据需求调整
vector prime; // 存所有质数
unordered_set pset; // 存质数(方便快速查询,可选)
vector tmp(maxValue + 1, 1); // 标记数组,tmp[i]=1 表示 i 是质数
void linearSieve()
{
// tmp[0]、tmp[1] 不是质数,直接置 0(可选,不影响核心逻辑)
tmp[0] = tmp[1] = 0;
for (int i = 2; i <= maxValue; ++i)
{
if (tmp[i] == 1) { // i 是质数
prime.push_back(i);
pset.insert(i);
}
// 用已找到的质数筛除合数
for (int j = 0; j < prime.size() && i * prime[j] <= maxValue; ++j)
{
tmp[i * prime[j]] = 0; // 标记为合数
if (i % prime[j] == 0)
{
break; // 保证每个合数只被最小质因数筛掉
}
}
}
}
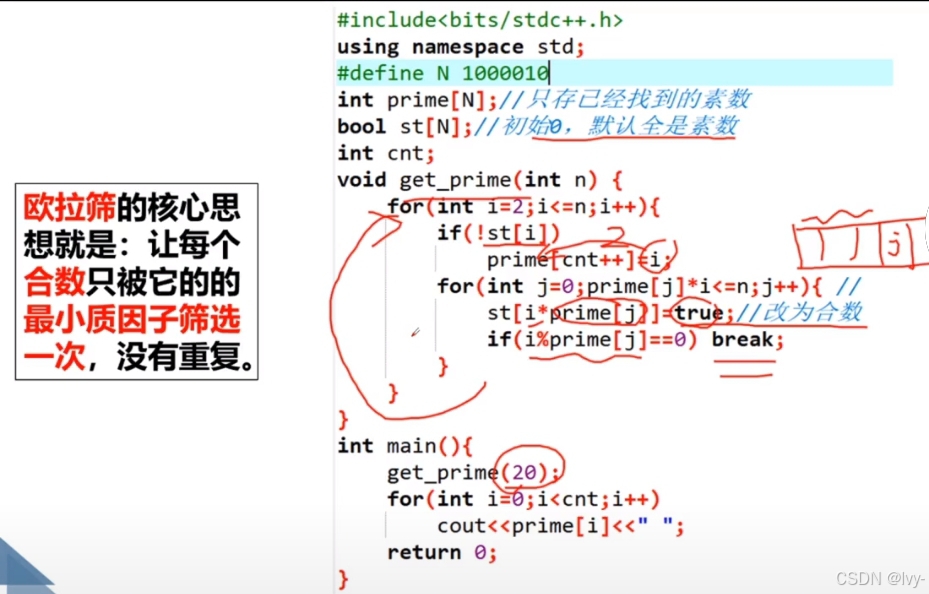
三、代码说明
1. 数组 tmp : tmp[i] == 1 表示 i 是质数,筛的过程中会把合数位置置 0。
2. prime 数组:动态存已找到的质数,用于后续筛法。
3. if (i % prime[j] == 0) break; :保证每个合数只被最小质因数筛掉,是线性筛效率的核心。
4. pset :用 unordered_set 存质数,方便快速查询“某个数是否是质数”(如果不需要查询,可去掉)。
如果想筛 [1, maxValue] 且保留 1,只需把 tmp[1] = 1 即可,但注意数学上 1 不是质数,实际场景中按需调整~


