LoRA 低秩矩阵实现参数高效的权重更新

LoRA 技术通过巧妙的设计，在保持原始线性层输入输出维度不变的前提下，用低秩矩阵实现参数高效的权重更新。让我用具体例子和图示解释它是如何 “改变维度” 的。

1. 标准线性层的维度变化

先回顾标准线性层 nn.Linear(d_in, d_out) 的工作方式：

• 输入：形状为 [batch_size, seq_len, d_in] 的张量（例如 [8, 10, 768]）。
• 权重矩阵：形状为 [d_out, d_in]（例如 [3072, 768]）。
• 输出：形状为 [batch_size, seq_len, d_out]（例如 [8, 10, 3072]）。

数学公式：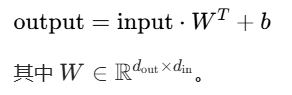

2. LoRA 线性层的维度变化

LoRA 线性层 lora.Linear(d_in, d_out, r=rank) 的核心是：

• 保留原始权重矩阵 W（冻结不更新）。
• 添加低秩分解的增量矩阵 

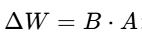
3. 维度变化示例

假设：

• 输入维度 d_in = 768，输出维度 d_out = 3072（Transformer 中常见的 MLP 扩展）。
• LoRA 秩参数 r = 8。

步骤分解：

1. 原始权重路径： 输入 [batch, seq_len, 768] → 乘以 \\(W^T\\)（形状 [768, 3072]）→ 输出 [batch, seq_len, 3072]。

2. LoRA 增量路径： 输入 [batch, seq_len, 768] →

   • 乘以 A^T（形状 [8, 768]）→ 中间结果 [batch, seq_len, 8]；
   • 再乘以 B^T形状 [3072, 8]）→ 最终增量 [batch, seq_len, 3072]。

3. 合并结果： 原始输出 + LoRA 增量 → 形状仍为 [batch, seq_len, 3072]。

4. 为什么这样设计？

LoRA 的核心是用低秩矩阵近似全秩更新，从而大幅减少参数：

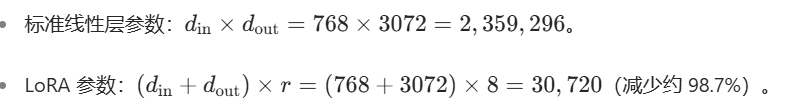
关键优势：

• 维度不变：输入输出维度与原始线性层完全一致，不改变模型架构。
• 计算高效：推理时可将 LoRA 权重合并到 W 中，无需额外计算。

5. 可视化对比

标准线性层：输入 [768] → [768×3072] → 输出 [3072]LoRA线性层：输入 [768] ────→ [768×3072]（冻结）─────┐  ↘  ↓ [768×8] → [8×3072] ──→ + → 输出 [3072]

6. 代码验证

以下代码验证 LoRA 线性层的维度变化：

import torchimport torch.nn as nn# 标准线性层linear = nn.Linear(768, 3072)# 简化的LoRA实现（实际库更复杂）class LoRALinear(nn.Module): def __init__(self, in_features, out_features, r=8): super().__init__() self.r = r # 原始权重（冻结） self.weight = nn.Parameter(torch.zeros(out_features, in_features), requires_grad=False) # LoRA权重 self.A = nn.Parameter(torch.randn(r, in_features) * 0.02) # [r, d_in] self.B = nn.Parameter(torch.zeros(out_features, r)) # [d_out, r] def forward(self, x): # 原始线性变换 out = nn.functional.linear(x, self.weight) # LoRA增量 lora_out = nn.functional.linear(x, self.B @ self.A) return out + lora_outlora_linear = LoRALinear(768, 3072, r=8)# 验证维度x = torch.randn(16, 10, 768) # [batch, seq_len, d_in]out_linear = linear(x)out_lora = lora_linear(x)print(f\"标准线性层输出形状: {out_linear.shape}\") # [16, 10, 3072]print(f\"LoRA线性层输出形状: {out_lora.shape}\") # [16, 10, 3072]

总结

LoRA 技术通过引入低秩矩阵（A 和 B）实现权重更新，但不改变输入输出的维度。它通过两次连续的线性变换（先降维到 r，再升维到 d_out，在保持计算效率的同时，用极少的参数实现模型适配。这正是 LoRA 的精妙之处：用低秩近似替代全秩更新，既节省资源，又不牺牲性能。