C语言中的数据结构--栈和队列（1）

前言

本届开始我们将对数据结构中栈的内容进行讲解,那么废话不多说,我们正式进入今天的学习

栈

栈是一种很特殊的线性表，它只能在固定的一端进行插入和删除操作，进行数据的插入和删除的一端叫做栈顶，另外一端叫做栈底，栈中的元素遵守后进先出的原则。

压栈：即数据的插入操作，在栈顶进行

出栈：即数据的删除操作，在栈顶进行

栈在内存中普遍采用顺序的存储结构，但是链式的存储结构也同样可行。因为在链式结构中寻找尾节点的时间较长，所以一般采取反向+头插入的操作来完成链式的存储，或者采用双向链表，但是不推荐，因为多一个向前的指针，会更加麻烦。本节仅对顺序存储结构进行讲解。两种存储方式各有优缺点(链式：没有扩容的消耗，更加节省空间        顺序：CPU高速缓存，效率更高)

「顺序表数据存储在连续的物理空间中，当CPU访问数据时，整个数据块可一次性加载到高速缓存中」

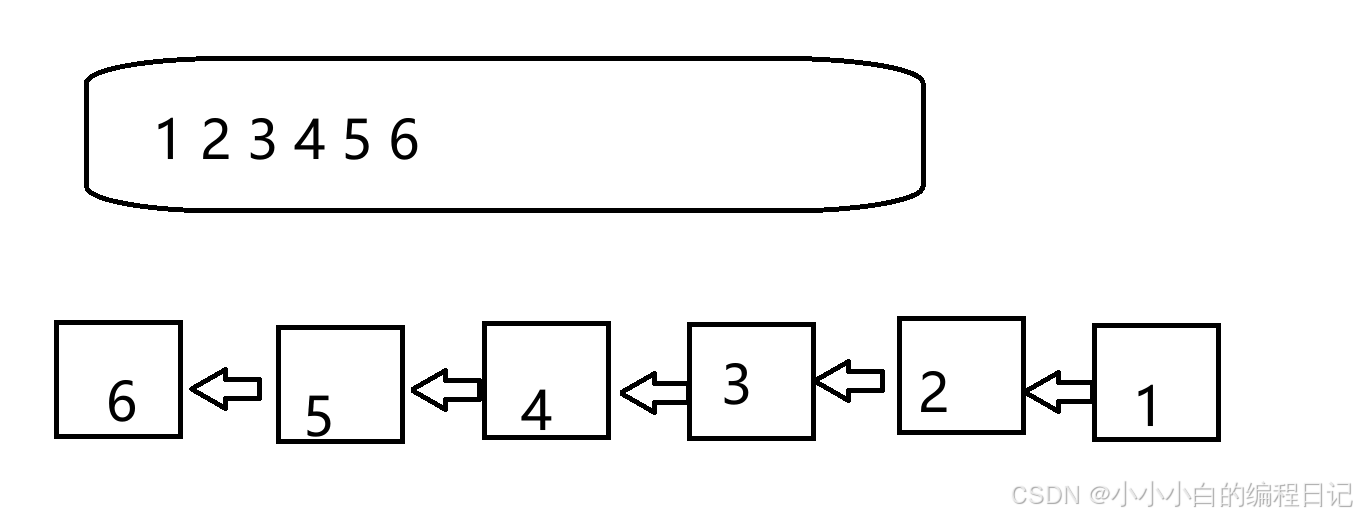
栈的基本存储结构

栈的基本存储结构如下所示（动态）：

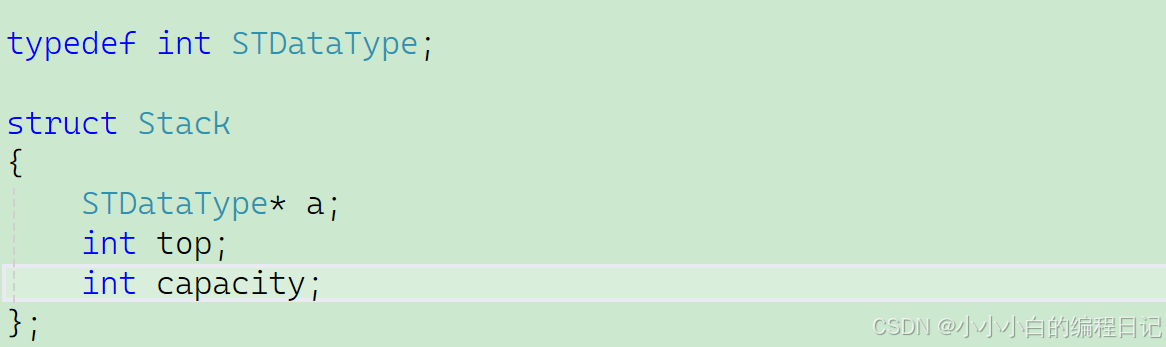
其中的top（栈顶）也可以称作size，a是栈的指针，capacity是栈的容量

栈的初始化和销毁

通过在C语言时期我们对指针的学习，我们可以知道：在初始化的函数之中，如果仅仅采取传值操作，形式参数的改变不会影响到实际参数，所以我们在初始化和销毁栈的过程之中要采取传地址的操作

在初始化栈的开头，我们需要加入assert进行断言，若为空则不采取操作

在数组开空间这一个步骤上，我们可以采取两种措施：第一种是开几个小的空间，后续再扩容；第二种是在初始化阶段先不进行空间的开辟，后续在处理的时候在开辟空间

（这里的代码采取的是不开辟空间，采用两种方法都是可以的）

栈的销毁代码非常简单，这里就不做过多的解释：

栈的入栈和出栈

栈的数据插入不像顺序表和链表一样，有头插入和尾插入。因为栈只能够在一端进行插入和删除，所以栈的操作只有压栈操作。

对于入栈的函数，我们需要用到的参数有：一个结构体指针pst、待插入的数据x

在开始书写栈的入栈代码之前，我们需要先明确一下top初始化时的指向。top的指向有两种：一种是指向栈顶元素，另外一种是指向栈顶数据下一个数据。(模拟实现的演示代码采取的是指向下一位)

当top指向当前元素的时候，如果栈中没有任何元素的时候，top的值应该要赋值为-1

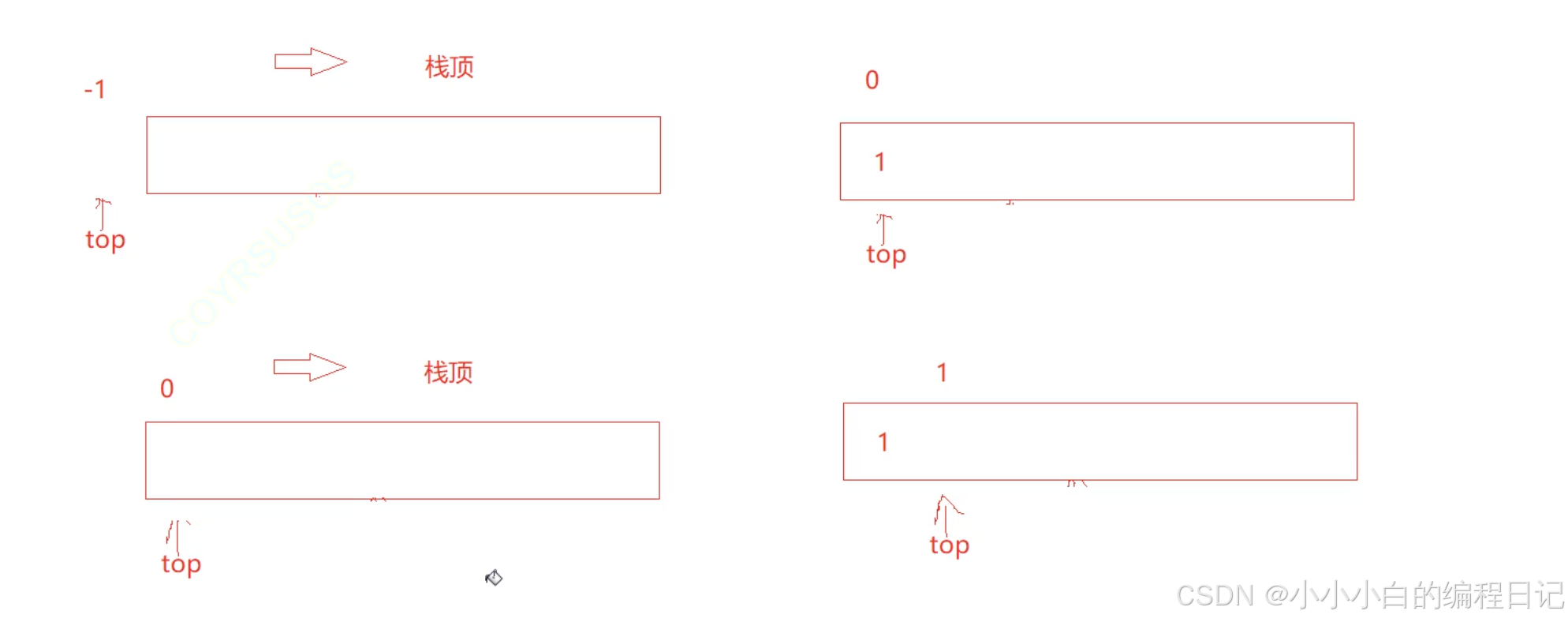
这两种指向的方式都是可以的，采取不同的指向方式时初始化top对应的赋值情况也不同：

假设我们采用的是第二种方法,那么我们在进行入栈时的操作就是:

pst->a[pst->top] = x;pst->top++;

而如果我们采取的是第一种方法,我们就需要让top先++再放入数据x 

接下来就是判断空间是否满了，满了的话就执行扩容操作。同样的，top在初始化时的指向不同时，判满的条件也不同。演示代码采取的是指向下一个元素的指向方法，所以判满的条件就是top等于capacity时:

void STPush(ST* pst, STDataType x){ assert(pst); //扩容 if(pst->top == pst->capacity) { int newcapacity = 2 * pst->capacity; STDataType* tmp = realloc(pst->a, newcapacity * sizeof(STDataType)); if(tmp == NULL) { perror(\"realloc fail\"); } pst->a = tmp; pst->capacity = newcapacity; } pst->a[pst->top++] = x;}

这里我故意提供了一个错误的代码,看看能不能发现问题

这里的代码存在的问题是:我们在初始化栈的时候采取了两种方式,第一种就是先给栈开辟一点小空间,此时采用这样的代码是不存在问题的,因为此时的capacity有数值;但是当我们采取第二种方法时,即不给栈开辟空间时,此时的capacity大小就是0,此时我们在newcapacity中的*2操作就会无效,所以我们在对new capacity进行操作的时候先需要判断一下capacity当前的大小:

int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;

那么假设栈一开始为空,此时的a也指向的是NULL,这样使用realloc会不会出现问题呢?答案是不会的,我们来查看一下realloc的使用说明:

从文档中我们可以清晰的看出,当指向的指针是空的时候,realloc函数相当于malloc函数

那么到此为止,入栈的代码就已经全部实现完成了,接下来我们来完成一下出栈的代码:

void STPop(ST* pst){ assert(pst); pst->top--;}

 到这里我们可能会有疑问,为什么STPop这短短的几行代码还需要封装成一个函数,为什么不能在使用的时候直接将代码写出来呢?就如同下面的代码一样:

 ST st; STInit(&st); STPush(&st, 1); STPush(&st, 2); STPush(&st, 3); STPush(&st, 4); STPop(&st); STPop(&st); STPop(&st); STPop(&st); //st.top--;

采取这样的方法其实也是可以的,但是这样会影响程序的可读性,所以这里不建议采取这样的形式.包括访问栈顶元素STTop中也建议采取封装的形式,不要直接访问:

STDataType STTop(ST* pst){ assert(pst); assert(pst->top > 0); return pst->a[pst->top - 1];}

我们自己直接去访问栈顶元素可能会出现错误,我们可能会忘记一开始设置top指针设置初始化的指向,导致不知道到底top是栈顶元素还是top-1是栈顶元素,如果直接将它封装成一个函数,就不会存在这样的问题

栈的其他接口实现

接下来我们来实现一下栈的判空操作,由于实现的逻辑非常简单,这里就不做过多地讲解了:

bool STEmpty(ST* pst){ assert(pst); if(pst->top == 0) return true; return false;}

接下来是返回栈的元素个数的接口:

int STSize(ST* pst){ assert(pst); return pst->top;}

因为栈的逻辑结构非常特殊,是采取的先进先出的结构,我们就不能采用类似于顺序表和链表那样的访问方式来访问栈.要想访问栈中的所有元素,我们就需要先用STTop来访问栈顶元素,然后执行STPop来删除栈顶元素,接着继续访问栈顶元素,一直循环到栈的元素为空为止

 while(!STEmpty(&st)) { printf(\"%d \", STTop(&st)); STPop(&st); }

但是采取这样的访问方式仍然存在一个问题:当我们访问完一次栈以后,栈里面所有的元素都被清空了,不便于我们后续的操作

其实这样的操作是合理的,我们期望的就是访问完栈中的某一个元素以后,后续就不能访问到这个元素了,这一点我们在后续的习题中会体现出来

练习题:有效的括号

我们来看一下这个练习题的题目:

刚看到这个题目的时候,我们最直接的思路就是数不同括号的数量,但其实这么做是没有用的,我们来举一个反例:\"[([)]]\",这组反例的数量是匹配的,但是它并不有效.所以这样的思路显然是不行的,在满足数量匹配的同时我们也要满足顺序的匹配

我们先来考虑一下什么时候需要考虑到括号匹配的问题:当我们取到右括号的时候我们才会需要考虑到括号匹配的问题,我们取到左括号的时候只需让他存入即可

结合这样的特征我们就可以考虑用栈来解决这个问题,当读取到左括号的时候只需要将其存入栈中即可.当读取到右括号的时候,因为最近的左括号在栈顶,我们就要它和最近的左括号匹配一下,如果匹配成功就让左括号也出栈

在写代码的时候我们需要注意,我们在确定是否匹配的时候判断的条件是不匹配就跳出,而不是判断匹配,因为就算是匹配了也需要进入下一次的检查:

 if((top == \'(\' && *s != \')\') || (top == \'[\' && *s != \']\') || (top == \'{\' && *s != \'}\')) return false;

到这里根据思路我们就可以初步完成代码:

bool isValid(char* s){ ST st; STInit(&st); while(*s) { if(*s == \'(\' || *s == \'[\' || *s == \'{\') STPush(&st, *s); else { char top = STTop(&st); STPop(&st); if((top == \'(\' && *s != \')\') || (top == \'[\' && *s != \']\') || (top == \'{\' && *s != \'}\')) return false; } ++s; } STDestory(&st); return true;}

当我们在提交代码的时候可以发现在某些情况下代码还是存在一定的问题:

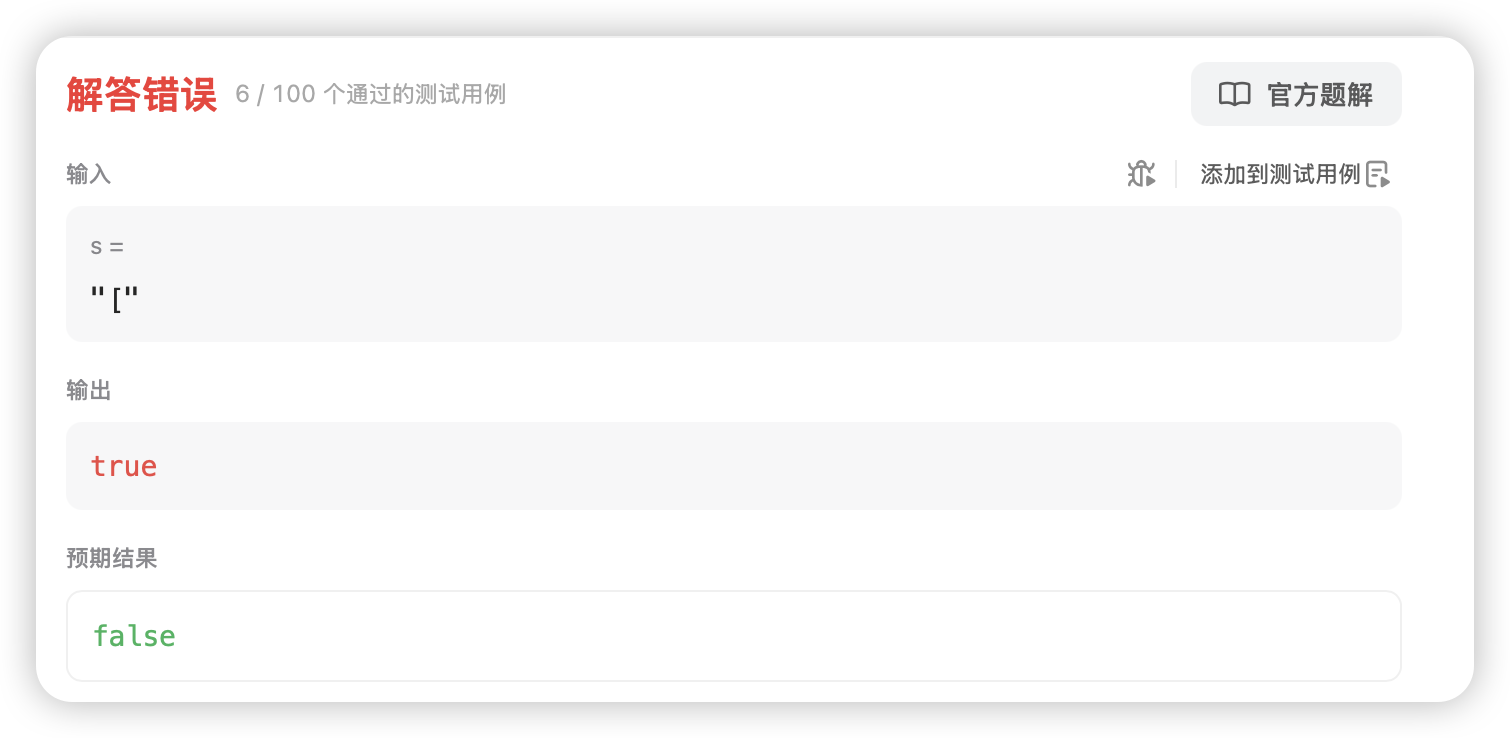
 在这样的情况之下,确实是不存在不匹配的问题,但是栈里面还有数据没有处理完,此时就意味着栈中还有左括号没有任何右括号供它匹配,说明左右括号的数量是不相等的,所以我们此时还需要加上判空的操作:

 //栈不为空 bool ret = STEmpty(&st); STDestory(&st); return ret;

我们再运行一下代码,发现还是存在问题,这里出现了一个断言错误:

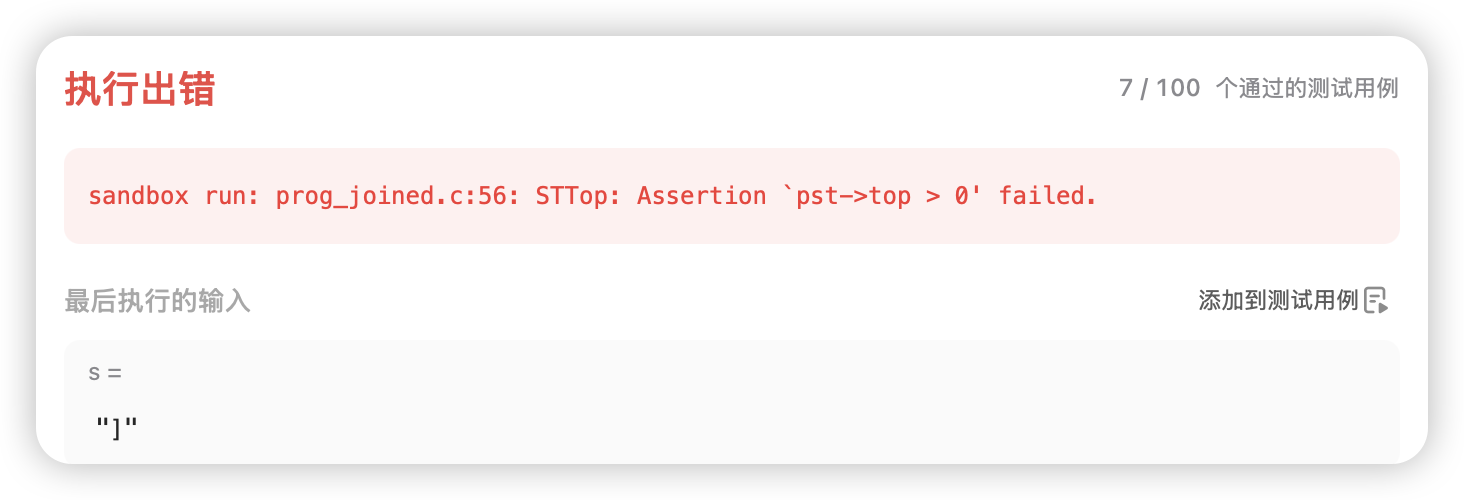
这里的意思是栈为空了以后我们还在调用栈,我们结合这里的测试用例来看一下:

这里给的用例是单独的一个右括号,所以会直接在栈中向前查找,寻找最近的左括号与之匹配,但由于栈中只有一个元素,所以此时再去向前查找就会导致越界,所以这里发生了断言错误.所以我们在判断右括号的时候还要加入一个判空的条件:

bool isValid(char* s){ ST st; STInit(&st); while(*s) { if(*s == \'(\' || *s == \'[\' || *s == \'{\') STPush(&st, *s); else { if(STEmpty(&st)) return false; char top = STTop(&st); STPop(&st); if((top == \'(\' && *s != \')\') || (top == \'[\' && *s != \']\') || (top == \'{\' && *s != \'}\')) return false; } ++s; } //栈不为空 bool ret = STEmpty(&st); STDestory(&st); return ret;}

修改完以后程序就没有问题了,但是如果我们仔细观察还是可以发现一些小的问题:可能会存在内存泄漏

假设栈中左括号的数量多于右括号的数量,在程序结束的时候就走不到后面的STDestory就已经直接返回了,此时就会存在内存泄漏.虽然这个并不会有太大的影响,但是我们还是要养成良好的习惯.

所以在这里,只要提前就false返回了,我们就对其执行STDestory:

 if(STEmpty(&st)) { STDestory(&st); return false; }

 if((top == \'(\' && *s != \')\') || (top == \'[\' && *s != \']\') || (top == \'{\' && *s != \'}\')) { STDestory(&st); return false; }

结尾

那么到此为止有关栈的内容就已经结束了,希望该文章可以给你带来帮助,下一节将对队列的内容进行梳理,谢谢你的浏览!!!!