数据结构——二叉树经典习题讲解_二叉树 简答题与解析

 各位看官早安午安晚安呀

如果您觉得这篇文章对您有帮助的话

欢迎您一键三连，小编尽全力做到更好
欢迎您分享给更多人哦

大家好，我们今天来学习java数据结构的二叉树

递归很重要的一些注意事项：

• 1：递归你能不能掌握在于：你能不能想清楚第一层非递归 以及 递归结束的条件（也就是最后一层递归，有时候递归结束的条件可能有好几个这很常见）（结束的条件仔细想一下是否能够合并呢？return root，return null，下一层root啥也没干，root == null，是否能够合并呢？这个其实无伤大雅，但是能合并尽量还是合并一下）（这两个场景你能够想清楚，你基本思路就没什么问题）
• 2：递归有返回值的
• 2.1：如果有返回值，你大概率是要接收你下一层递归的返回值（）（然后你进行整理完之后继续向上返回）
• 2.2：递归如果返回值是要叠加的，譬如求二叉树的高度的，这个返回值一定要接收。

1.1.判断两个二叉树是否相等

链接

 public boolean isSameTree(TreeNode p, TreeNode q) { if(p == null && q != null || p != null && q == null){ //结构不一样不相等 return false; } if(p == null && q == null){ // 看你俩只要同时为空就相等 return true; } return p.val == q.val && isSameTree(p.left,q.left) && isSameTree(p.right,q.right); }

1.2.相同的二叉树

相同的树

public boolean isSameTree(TreeNode p, TreeNode q) { if(p == null && q != null || p != null && q == null){ return false; } if(p == null && q == null){ return true; } return p.val == q.val && isSameTree(p.left,q.left) && isSameTree(p.right,q.right); } public boolean isSubtree(TreeNode root, TreeNode subRoot) { if(isSameTree(root,subRoot)){ //判断一开始就是否相等 return true; } if(root == null){ return false; } if(isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot)){ //左边和右边一个相等就行 //其实这个就是前序遍历，利用返回值 return true; } return false; }

1.3.翻转二叉树

翻转二叉树

public TreeNode invertTree(TreeNode root) { if(root == null){ return null; }  //交换节点 TreeNode tmp = root.left; root.left = root.right; root.right = tmp;//翻转 invertTree(root.left); invertTree(root.right); return root; }

1.4.平衡二叉树

平衡二叉树

补充知识点:

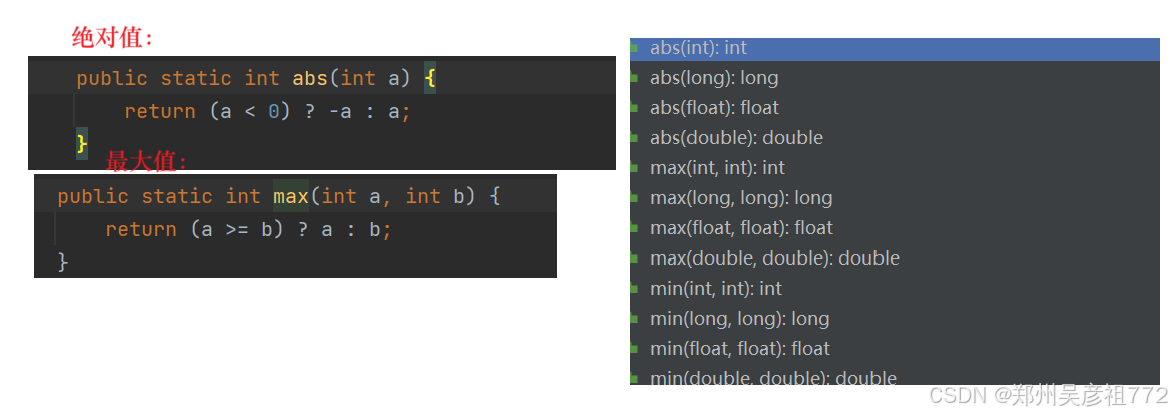
 //更改的平衡二叉树，因为我们在算高度的时候每一颗子树的高度我们都算过,我们完全可以算整个树的高度 //然后进行顺带算两边的高度差是否 <= 1,一次性算完 int getHeight2(TreeNode root){ if(root == null){ return 0; } //左树高度和右树高度 int leftHeight = getHeight2(root.left); int rightHeight = getHeight2(root.right); //两边高度差<= 1并且都大于0（任何一个高度为-1的时候，整个树的返回值就为-1（-1代表不平衡）） // 只要有一个-1返回，那么之后都是返回-1，不平衡 if(Math.abs(leftHeight - rightHeight) = 0 && rightHeight >= 0){ return Math.max(leftHeight,rightHeight)+1; } return -1; } public boolean isBalanced(TreeNode root) { if(root == null){ return true; } return getHeight2(root) >= 0; }

1.5.对称二叉树

对称二叉树

public boolean isSymmetric(TreeNode root) { if(root == null){ return true; } //我要看是否对称，肯定要两个节点进行比较，要两个变量  return isSample(root.left,root.right); } public boolean isSample(TreeNode p , TreeNode q){ //两边都是空的，就一个根，直接返回true if( p == null && q == null){ return true; } //一个为空另一个不为空，直接返回false if( p == null || q == null){ return false; } if(p.val != q.val){ return false; } return isSample(p.left,q.right) && isSample(p.right,q.left); }

1.6.通过字符串构建二叉树

通过字符串构建二叉树

import java.util.Scanner;class TreeNode{ char val; TreeNode left; TreeNode right; public TreeNode(){ } public TreeNode(char val){ this.val = val; }}// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); // 注意 hasNext 和 hasNextLine 的区别 while (in.hasNextLine()) { // 注意 while 处理多个 case String str = in.nextLine(); //创建二叉树 TreeNode root = create(str); //中序遍历 inorder(root); } } public static int i = 0; public static TreeNode create(String str){ //递归的第一层要素就是要知道什么时候结束 // 首先我们遇到 “#” 就要返回 ,但是我们的i还是要先++ 后返回 if(str.charAt(i) == \'#\'){//但是我们要考虑的是，我们就算是返回了，我们的遍历str的i还是要往前走 i++; return null; }else{ TreeNode root = new TreeNode(str.charAt(i)); i++; root.left = create(str); root.right = create(str); return root; }//最后你会发现其实这两个返回值可以合并成一个，//其实每次递归题大家都可以看一下 }//中序遍历 public static void inorder(TreeNode root){ if(root == null){ return; } inorder(root.left); System.out.print(root.val +\" \"); inorder(root.right); }}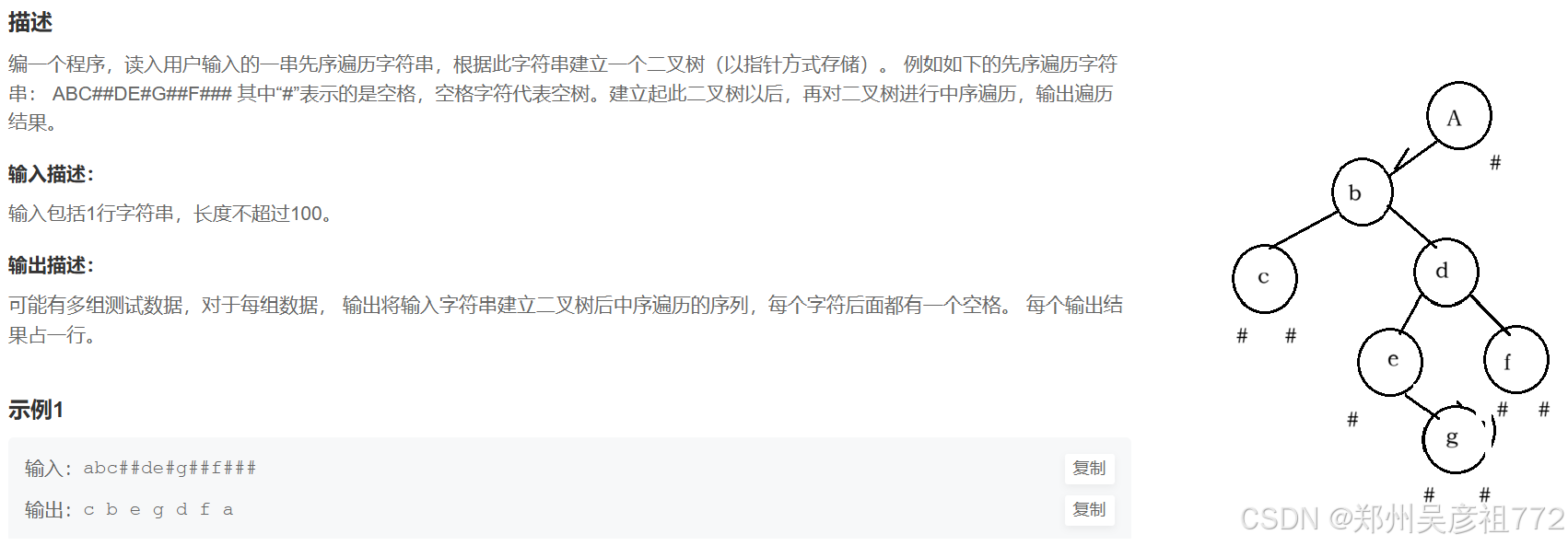

1.7.二叉树分层遍历：

二叉树的层序遍历

public List<List> levelOrder(TreeNode root) { List<List> list = new ArrayList();//别问 问就是OJ的测试用例让我这么干的 // root = [] 预期结果[]，所以下面返回的也是List而不是null if(root == null){ //如果根节点都是null，就不用遍历了 return list; } // 先把 根节点add进去队列里面 Queue queue = new LinkedList(); queue.offer(root); //tmp.add(root);//这里不对呀，最后一倍一倍的增长。这个size也不对，看我下面如何修改 while(!queue.isEmpty()) { //int size = tmp.size(); List tmp = new ArrayList();//这个可不敢放在一开始呀，不然又叠加了(ArrayList好一点) int size = queue.size();//计算上一次add进来的总和， 下面直接就是 size!=0,这完全就是要把上一次的全poll出去 while (size != 0) { //和上一个的区别就在于，上一个层序遍历是一个一个出队列的，这个是一次性把上一次add进来的全部poll出去 TreeNode cur = queue.poll(); tmp.add(cur.val);  // System.out.println(cur.val + \" \"); size--;//记得--; if (cur.left != null) {  queue.offer(cur.left); } if (cur.right != null) {  queue.offer(cur.right); } } list.add(tmp); } return list; }

1.8.二叉树的最近公共祖先

二叉树的最近公共祖先

 public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if(p == root || q == root){ return root; } if(root == null){ return null; } TreeNode leftRoot = lowestCommonAncestor(root.left,p,q); TreeNode rightRoot = lowestCommonAncestor(root.right,p,q); if(leftRoot != null && rightRoot != null){ return root; } else if (leftRoot != null) { return leftRoot; }else{ return rightRoot; } }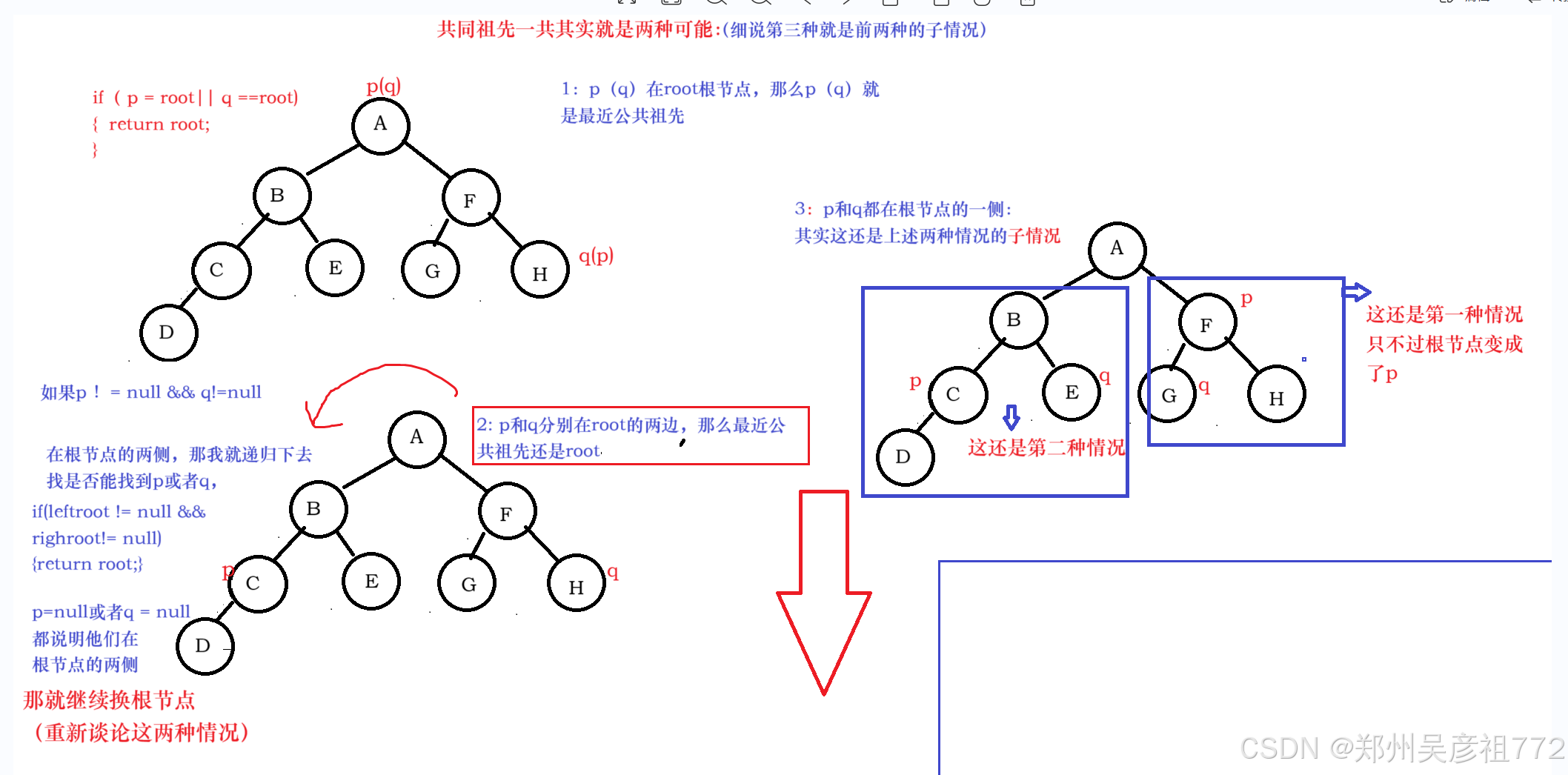

解法二：看成两个链表相交，找相交点

private boolean getPath(TreeNode root,TreeNode node,Stackstack){ // 判断这个节点是不是这个路径上的节点(如果不是，看看它的左子树和右子树是不是这个路径上的节点如果都不是) //就返回false，把这个节点pop出来 if(root == null || node == null){ return false; } stack.push(root); //一定要压进去，不然root == node 导致这个栈里面没有了元素 if(root == node){ return true; } boolean flg1 = getPath(root.left,node,stack); //看看左节点有没有 if(flg1){ return true; } boolean flg2 = getPath(root.right,node,stack); //看看右节点有没有 if(flg2){ return true; } //都没有就return false stack.pop(); return false; } public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { Stackstack1 = new Stack(); Stackstack2 = new Stack(); //利用getPath初始化这两个栈 getPath(root,p,stack1); getPath(root,q,stack2); //初始化之后，进行比较，让长栈先走size步 int size = stack1.size() -stack2.size(); if(size > 0){ while(size != 0){ stack1.pop(); size--; } }else{ while(size != 0){ stack2.pop(); size++; } } while(!stack1.isEmpty() && ! stack2.isEmpty()){ //&&后面的写不写都行 if(stack1.peek().equals(stack2.peek())){ return stack1.peek(); } stack1.pop(); stack2.pop(); } return null; }

1.9. 从前序与中序遍历序列构造二叉树

 从前序与中序遍历序列构造二叉树

class Solution { public int preIndex;//一定要设置成成员变量（全局效果），局部变量的话放方法参数里，每次都是传值调用 //不能保证preIndex一直往前走 public TreeNode buildTree(int[] preorder, int[] inorder) { return buildTreeChild(preorder,inorder,0,inorder.length -1); } private TreeNode buildTreeChild(int[] preorder,int[] inorder,int inbegin,int inend){ if(inbegin > inend ){ //其实这里的结束有两次，inbegin = inend 也应该结束（但是合并成一种情况了） return null; } if(inbegin == inend){ int pre = preIndex; preIndex++;  return new TreeNode(preorder[pre]); } //先看这个（前序遍历的）节点是否在中序遍历的这个范围内，在的话我再把这个根节点给创建出来 int rootIndex = findIndex(inorder,inbegin,inend,preorder[preIndex]); if(rootIndex == -1){ return null; } TreeNode root = new TreeNode(preorder[preIndex]); preIndex++; root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1); root.right = buildTreeChild(preorder,inorder,rootIndex + 1,inend); return root; } private int findIndex(int[] inorder,int inbegin,int inend,int key){ for(int i = inbegin; i<= inend ; i++){ if(inorder[i] == key){ return i; } } return -1; }}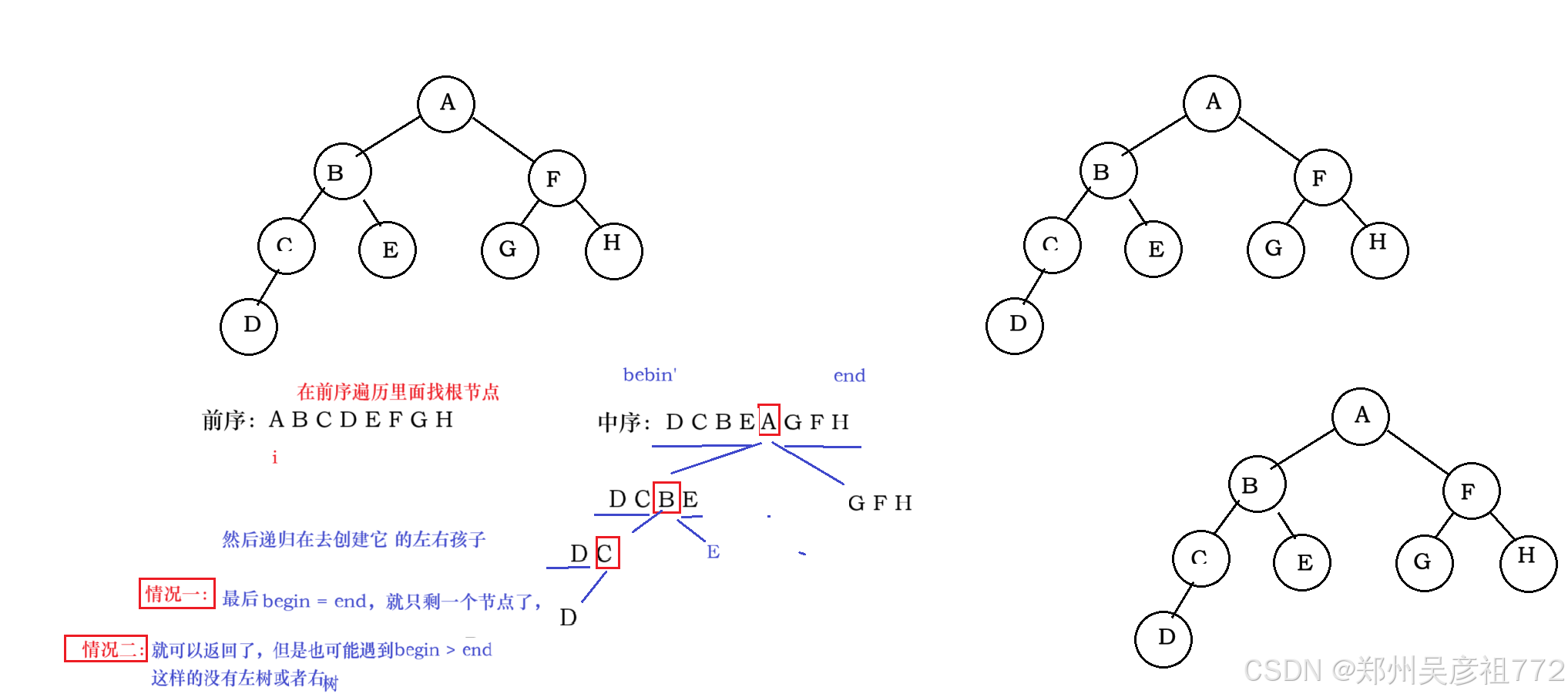

1.10.从中序与后序遍历序列构造二叉树

如果后序：是先递归右树，再左树，再根（此刻的后序的字符串就是前序的逆转）

1从中序与后序遍历序列构造二叉树

class Solution { public int postIndex ;//一定要设置成成员变量（全局效果），局部变量的话放方法参数里，每次都是传值调用 //不能保证preIndex一直往前走 public TreeNode buildTree(int[] inorder, int[] postorder) { postIndex = postorder.length -1; return buildTreeChild(postorder,inorder,0,inorder.length -1); } private TreeNode buildTreeChild(int[] postorder,int[] inorder,int inbegin,int inend){ if(inbegin > inend ){ //其实这里的结束有两次，inbegin = inend 也应该结束（但是合并成一种情况了） return null; } //先看这个（前序遍历的）节点是否在中序遍历的这个范围内，在的话我再把这个根节点给创建出来 int rootIndex = findIndex(inorder,inbegin,inend,postorder[postIndex]); if(rootIndex == -1){ return null; } TreeNode root = new TreeNode(postorder[postIndex]); postIndex--; root.right = buildTreeChild(postorder,inorder,rootIndex + 1,inend); root.left = buildTreeChild(postorder,inorder,inbegin,rootIndex-1); return root; } private int findIndex(int[] inorder,int inbegin,int inend,int key){ for(int i = inbegin; i<= inend ; i++){ if(inorder[i] == key){ return i; } } return -1; }}

1.11.前序遍历二叉树（迭代实现）

 public static void preOrder1(TreeNode root) { if (root == null) { return; } //本质上这还是递归的思想（stack还是往回走，不然你路上的节点，没办法遍历他的右边； Stack stack = new Stack(); TreeNode cur = root; while (cur != null || !stack.isEmpty()) {// 加个cur !=null,纯粹是因为，第一次stack是空的 while (cur != null) {//一直往 System.out.print(cur.val); stack.push(cur); cur = cur.left; //其实一开始我是这么想的 /*if(cur == null){ cur = stack.pop(); cur = cur.right; //但是这样就废了呀，右边为空就完蛋了，循环结束，gameOver }*/ } //左边为空，直接就拿回我上一个根，然后打印右边 cur = stack.pop(); cur = cur.right; } }

1.11.中序遍历二叉树（迭代实现）

public static void inOrder1(TreeNode root) { if (root == null) { return; } //本质上这还是递归的思想（stack还是往回走，不然你路上的节点，没办法遍历他的右边； Stack stack = new Stack(); TreeNode cur = root; while (cur != null || !stack.isEmpty()) {// 加个cur !=null,纯粹是因为，第一次stack是空的 while (cur != null) {//一直往 stack.push(cur); cur = cur.left; } //左边为空，直接就拿回我上一个根，然后打印右边 cur = stack.pop(); System.out.print(cur.val); cur = cur.right; } }

1.11.后序遍历二叉树（迭代实现）

 //根据字符串循环进行后序遍历 public static void postOrder1(TreeNode root) { if (root == null) { return; } //本质上这还是递归的思想（stack还是往回走，不然你路上的节点，没办法遍历他的右边； Stack stack = new Stack(); TreeNode cur = root; TreeNode prev = null; TreeNode top = null; while (cur != null || !stack.isEmpty()) {// 加个cur !=null,纯粹是因为，第一次stack是空的 while (cur != null) {//一直往 stack.push(cur); cur = cur.left; } //左边为空，直接就拿回我上一个根，然后打印右边 top = stack.peek(); if(top .right == null || top.right == prev){ stack.pop(); System.out.print(top.val + \" \"); prev = top; }else { // 右边不为空不能pop cur = top.right; } } }

上述就是二叉树习题讲解的全部内容了，能看到这里相信您一定对小编的文章有了一定的认可，二叉树的出现让我们对于数据的组织的利用有了更加方便的使用~~

有什么问题欢迎各位大佬指出
欢迎各位大佬评论区留言修正

您的支持就是我最大的动力​​​！！！！