双指针算法介绍及使用(下)
在上一篇文章中我们已经对双指针有了一定了解,接下来我们通过题目来对双指针进行更好的理解。
1. leetcode 202. 快乐数

这道题使用的方法是快慢指针, 比如说一个数X,那么创建两个变量X1和X2,然后X1每次变化两次,X2变化一次,那么X1和X2肯定会相遇(假如说X不是快乐数,那么X1和X2会在一个变化范围内相遇,反之就是在1的位置相遇)。
PS:这道题在我看来不是传统意义上的快慢指针,在我看来跟多的是使用了其思想。
我们在代码里面使用了slow和fast两个指针来模拟相遇。
class Solution {public: int happysum(int a) { int count=0; while(a) { int b=a%10; count+=b*b; a/=10; } return count; } bool isHappy(int n) { int slow=n; int fast=n; fast=happysum(fast); while(slow!=fast) { slow=happysum(slow); fast=happysum(fast); fast=happysum(fast); } return fast==1; }};2. leetcode 11. 盛最多水的容器
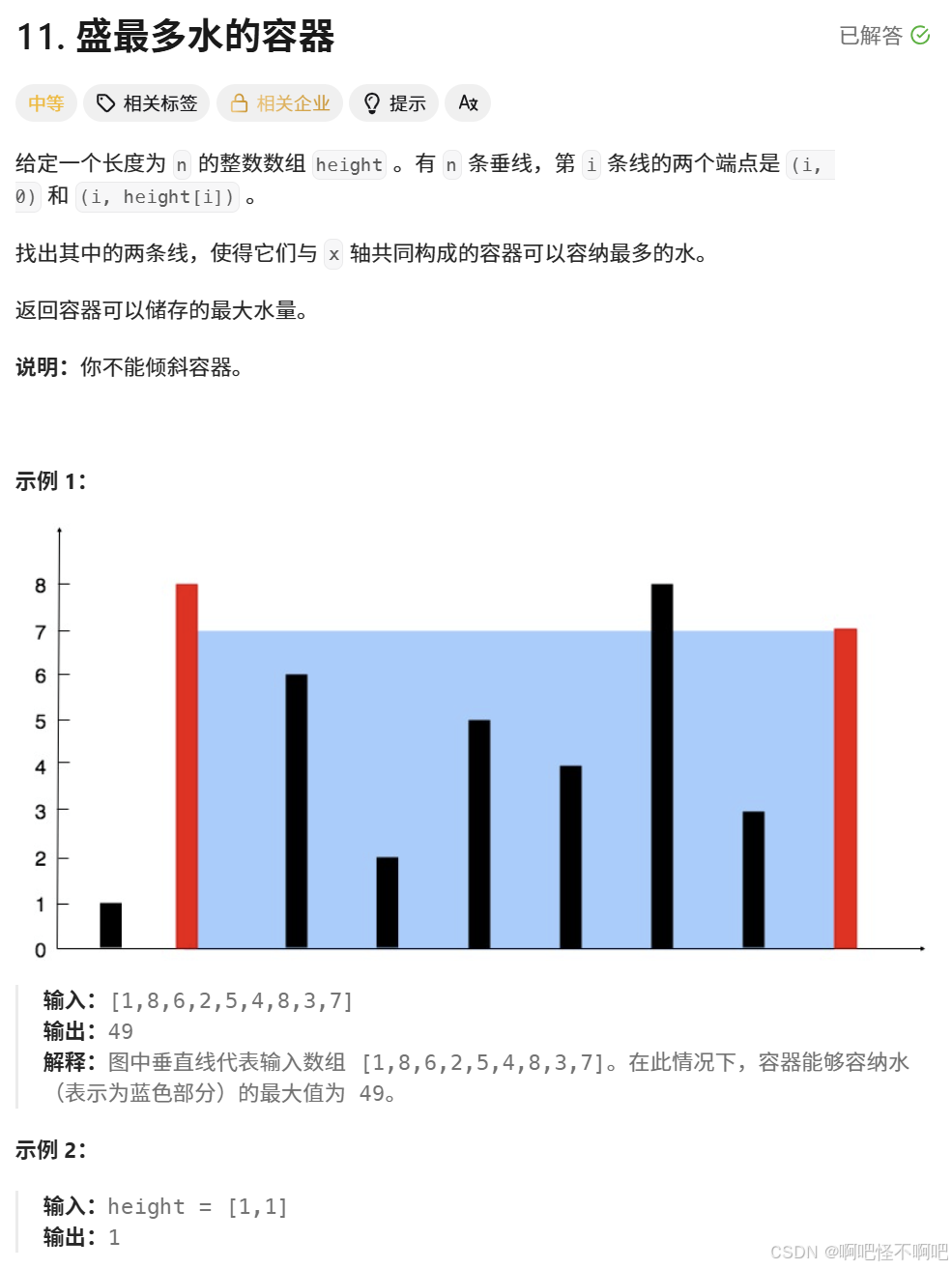
这道题的话暴力是肯定不行的,那么我们可以通过左右指针的方式 。简单来说就是最左和最右两边先进行一次计算,然后哪边短哪边移动,然后比较这几个值的大小就可以得到结果。
PS:我们也可以理解为计算横坐标在某个值时的最大值。
class Solution {public: int maxArea(vector& h) { int left=0; int n=h.size()-1; int right=n; int mymax=0; while(left=h[right]) right--; else left++; mymax=max(mymax,count); } return mymax; }};3. leetcode 611. 有效三角形的个数

三角形三边需满足 “任意两边之和大于第三边”,但直接枚举所有三元组验证效率低(时间复杂度高)。所以需要利用排序 + 双指针优化。
简单来说,就是先拿一个最大的,然后在剩下的里面通过left++和right--来直接找到符合的区间,因为实现排好序了所以一旦找到直接right-left就可以了。
class Solution {public: int triangleNumber(vector& nums) { int count=0; sort(nums.begin(),nums.end()); int n=nums.size()-1; for(int i=n;i>=2;--i) { int left=0; int right=i-1; while(left!=right) { if(nums[left]+nums[right]>nums[i]) { count+=right-left; right--; } else { left++; } } } return count; }};4. leetcode LCR 179. 查找总价格为目标值的两个商品

这道题也可以通过二分的方式来进行解决,在这里我们通过双指针的方式来进行解决。
简单来说就是先设一个left和一个right,然后通过t-p[left]的方式来得到一个值(即以p[left]为确定值的前提来查找有没有另一个值)。因为这个数组是升序的,所以说如果找不到就说明是p[left]太小了,所以left++即可。
class Solution {public: vector twoSum(vector& p, int t) { int n=p.size(); int left=0; vector v; for(left=0;;++left) { int right=n-1; while(leftp[right]) break; else if(t-p[left]<p[right]) { right--; } else { v.push_back(p[left]); v.push_back(p[right]); return v; } } } }};5. leetcode 15. 三数之和

这道题的话就和上面那到类似,唯一要注意的就是题目要求中说答案中不可以包含重复的三元组。
所以我们要先对其进行去重。三个数都有可能重复,所以三个数都要检查一下。
class Solution {public: vector<vector> threeSum(vector& nums) { sort(nums.begin(),nums.end()); vector<vector> v; int n=nums.size(); for(int i=0;i0&&nums[i]==nums[i-1]) continue; int left=i+1; int right=n-1; int t=nums[i]; while(left0) { right--; } else if(t+nums[left]+nums[right]<0) { left++; } else { v.push_back({nums[i],nums[left],nums[right]}); while(left<right&&nums[left]==nums[left+1]) left++; while(left<right&&nums[right]==nums[right-1]) right--; right--; left++; } } } return v; }};

