网站导航
> 技术文档 > 动态规划与01背包问题：蓝桥杯备赛指南_蓝桥杯动态规划考的多吗

动态规划与01背包问题：蓝桥杯备赛指南_蓝桥杯动态规划考的多吗

网友: 技术文档 2025-07-30 11:10:33

在蓝桥杯比赛中，动态规划是高频考点之一，而01背包问题则是动态规划的经典应用。掌握这些知识，不仅能帮助你在比赛中取得好成绩，还能提升你解决复杂问题的能力。本文将详细介绍动态规划的基本概念、01背包问题的解法，并分别用Java、C语言和Python实现这些算法。

一、动态规划基础

（一）动态规划是什么

动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。它通常用于解决具有重叠子问题和最优子结构特性的问题。

（二）动态规划的基本要素

  1. 最优子结构：如果一个问题的最优解包含其子问题的最优解，那么这个问题具有最优子结构。

  2. 重叠子问题：在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。

  3. 状态转移方程：描述问题的最优解与子问题最优解之间的关系。

二、01背包问题

（一）问题描述

假设你有一个背包，其最大容量为W，同时有N个物品，每个物品有对应的重量w[i]和价值v[i]。每个物品只能选择放或不放，目标是让背包中物品的总价值最大。

（二）解题思路

  1. 定义状态：dp[j]表示容量为j的背包所能达到的最大价值。

  2. 状态转移方程：对于每个物品i，如果它的重量w[i]小于等于当前背包容量j，则dp[j] = max(dp[j], dp[j - w[i]] + v[i])。

  3. 初始化：dp[0] = 0，表示容量为0的背包价值为0。

  4. 遍历顺序：通常从后往前遍历背包容量，以避免重复计算。

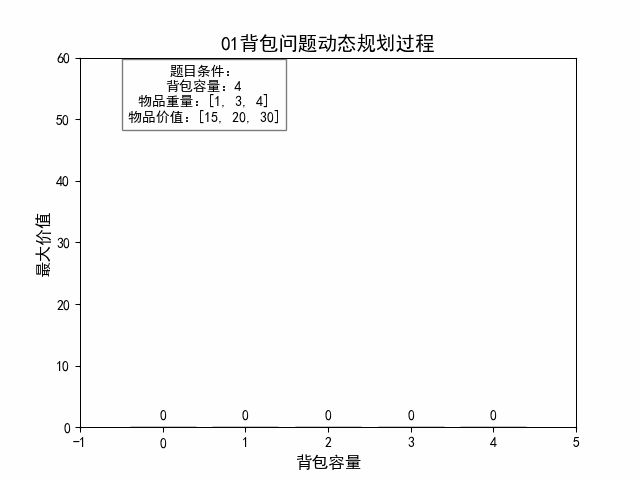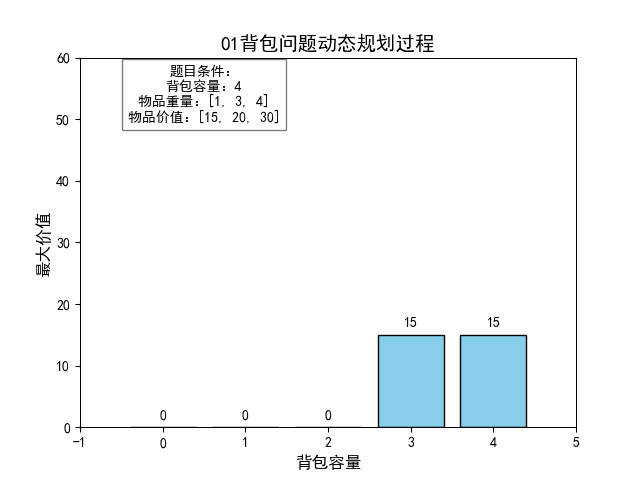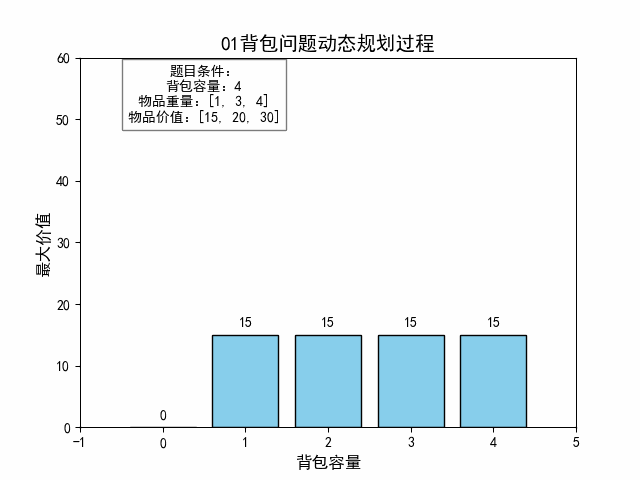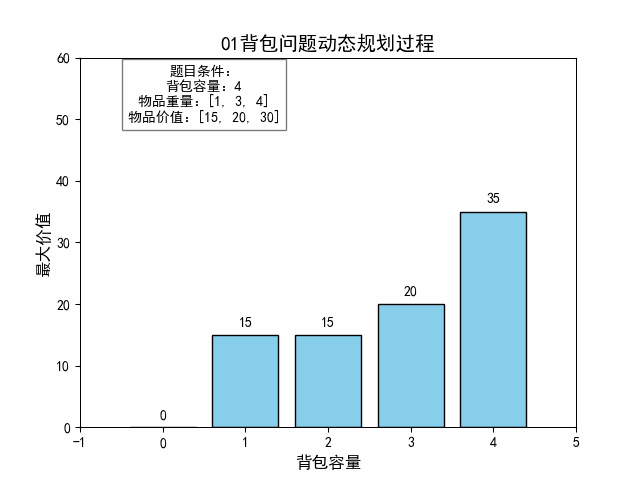
（三）Java代码实现

以下是01背包问题的Java代码实现：

public class Knapsack { public static int knapsack(int[] weights, int[] values, int capacity) { int n = weights.length; int[] dp = new int[capacity + 1]; for (int i = 0; i = weights[i]; j--) { dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]); } } return dp[capacity]; } public static void main(String[] args) { int[] weights = {1, 3, 4}; int[] values = {15, 20, 30}; int capacity = 4; int maxProfit = knapsack(weights, values, capacity); System.out.println(\"最大价值为: \" + maxProfit); }}

（四）C语言代码实现

以下是01背包问题的C语言代码实现：

#include #define N 5#define W 11void knapsack01(int result[N + 1][W + 1], int w[N + 1], int v[N + 1]) { int i, j; for (i = 1; i <= N; i++) { for (j = 1; j <= W; j++) { if (j  (v[i] + result[i - 1][j - w[i]]) ? result[i - 1][j] : (v[i] + result[i - 1][j - w[i]]); } }}void select(int result[N + 1][W + 1], int w[N + 1], int v[N + 1]) { int n = N; int bagw = W; while (n > 0) { if (result[n][bagw] == result[n - 1][bagw]) { n--; } else { printf(\"(%d,%d) \", w[n], v[n]); bagw = bagw - w[n]; n--; } }}int main() { int w[N + 1] = {0, 1, 2, 5, 6, 7}; int v[N + 1] = {0, 1, 6, 18, 22, 28}; int result[N + 1][W + 1] = {0}; knapsack01(result, w, v); printf(\"背包承重为 %d,最大收益为 %d\\n\", W, result[N][W]); printf(\"选择了：\"); select(result, w, v); return 0;}

（五）Python代码实现

以下是01背包问题的Python代码实现：

N = 5W = 11w = [0, 1, 2, 5, 6, 7]v = [0, 1, 6, 18, 22, 28]result = [[0] * (W + 1) for _ in range(N + 1)]def knapsack01(): for i in range(1, N + 1): for j in range(1, W + 1): if j  0: if result[n][bagw] == result[n - 1][bagw]: n -= 1 else: print(\"(%d,%d) \" % (w[n], v[n]), end=\"\") bagw -= w[n] n -= 1print(\"所选商品为:\")select()

（六）优化与扩展

  1. 空间优化：上述代码已经将空间复杂度优化到O(W)，通过一维数组实现了动态规划。

  2. 完全背包与多重背包：完全背包问题允许每个物品无限次使用，而多重背包问题允许每个物品使用有限次。它们的状态转移方程与01背包类似，但遍历顺序有所不同。

（七）例题讲解

力扣2742给墙壁刷油漆https://leetcode.cn/problems/painting-the-walls/solutions/3624614/dong-tai-gui-hua-zhuan-wei-01bei-bao-by-updod

力扣LCP47.入场安检https://leetcode.cn/problems/oPs9Bm/solutions/3623372/01bei-bao-dpfa-by-xiongkailiang-96rp

三、动态规划在蓝桥杯中的应用

（一）常见题型

  1. 最长公共子序列（LCS）：给定两个字符串，求它们的最长公共子序列长度。

  2. 最长递增子序列（LIS）：给定一个数组，求最长递增子序列的长度。

  3. 数字三角形：从一个数字三角形的顶部走到底部，求路径上数字的最大和。

（二）解题技巧

  1. 状态定义：清晰定义dp数组的含义，这是解题的关键。

  2. 边界条件：注意初始化条件和边界情况。

  3. 状态转移：根据问题的性质，推导状态转移方程。

四、总结

动态规划和01背包问题是蓝桥杯比赛中非常重要的知识点。通过理解动态规划的基本概念和掌握01背包问题的解题思路，你可以解决很多类似的算法问题。希望本文的介绍和代码示例能帮助你在蓝桥杯比赛中取得优异成绩。

如果你对动态规划和01背包问题还有疑问，或者想了解更多相关算法，欢迎在评论区留言，我会为你解答。

网络标签：

相关问题