大话数据结构之 ＜ 栈＞（C语言）

引言：栈（Stack）是一种重要的线性数据结构，它遵循 **“后进先出”（Last In, First Out，简称 LIFO）** 的原则，即最后放入栈中的元素会最先被取出。这种特性使得栈在很多场景中都有广泛应用，比如程序调用的栈帧管理、表达式求值、括号匹配等。本章介绍栈，包括其实现。

1.栈的概念及结构

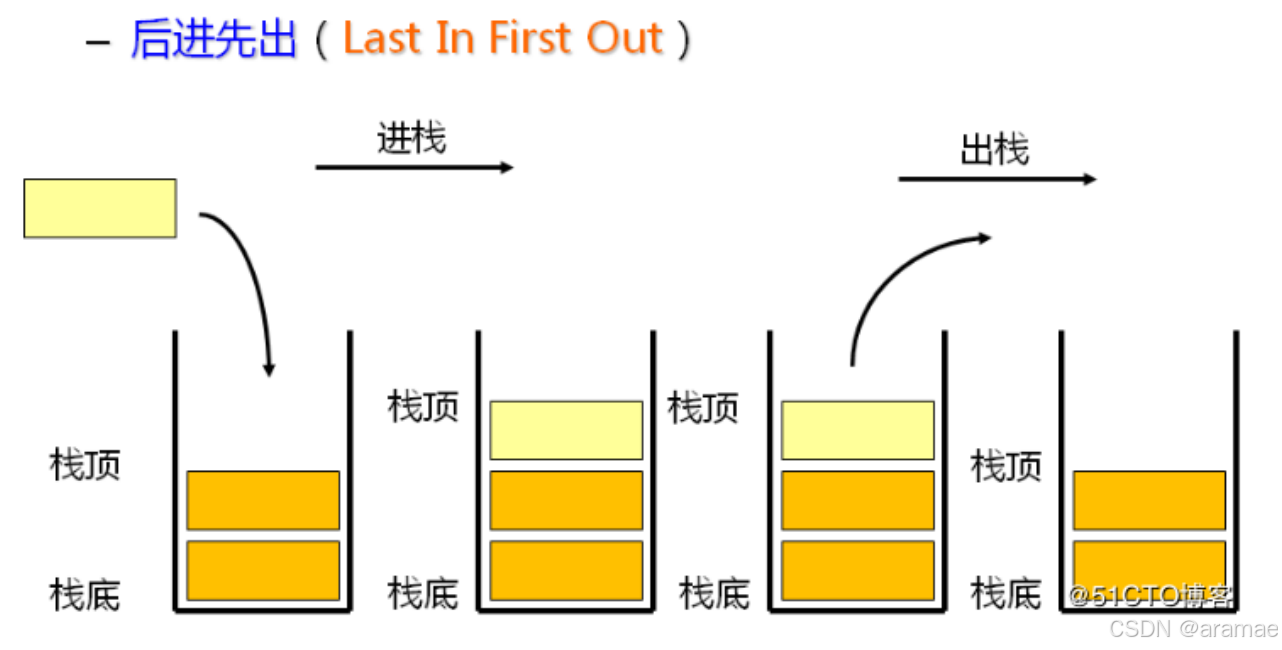
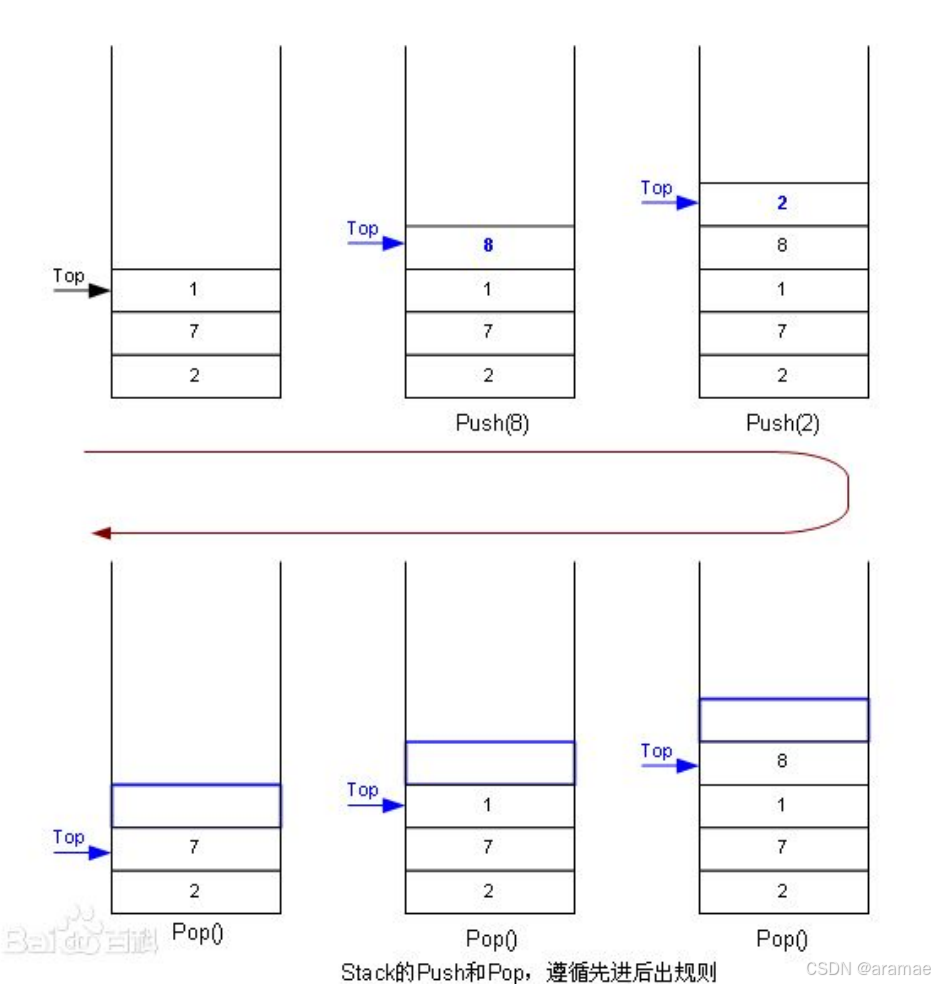
栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端 称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

• 压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
• 出栈：栈的删除操作叫做出栈。出数据也在栈顶

2.栈的实现

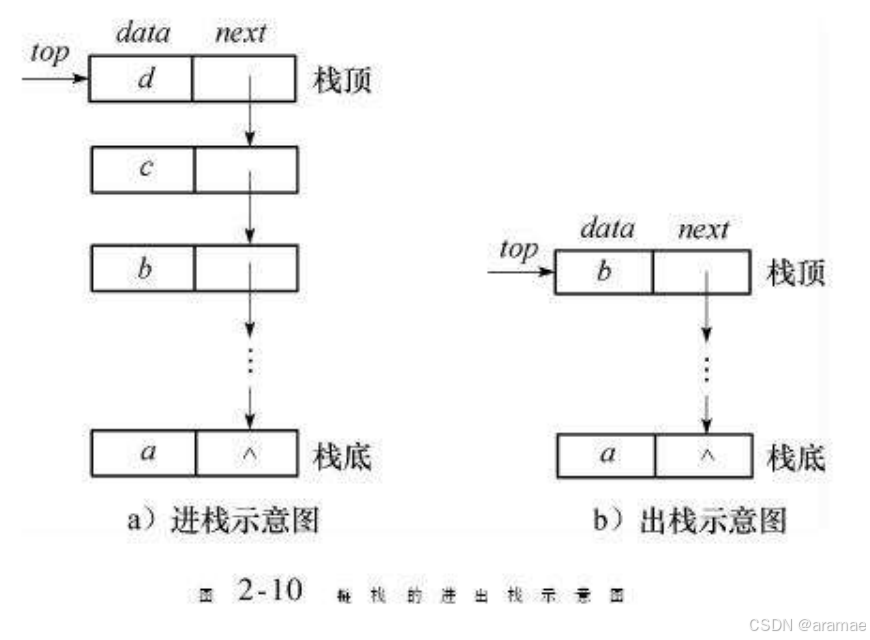
栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。（即栈是一种基于数组或链表实现的数据结构，其拥有自身的特性）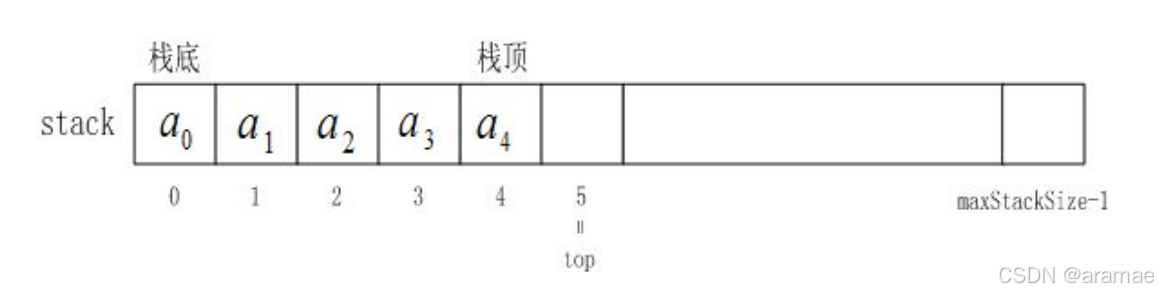

数组实现（静态顺序栈）

#include #include #define MAX_SIZE 100 // 栈的最大容量// 数组实现的栈结构typedef struct { int data[MAX_SIZE]; // 静态数组存储栈元素 int top; // 栈顶指针} ArrayStack;// 初始化栈void initArrayStack(ArrayStack *stack) { stack->top = -1; // 初始化为-1表示空栈}// 判断栈是否为空bool isArrayStackEmpty(ArrayStack *stack) { return stack->top == -1;}// 判断栈是否已满bool isArrayStackFull(ArrayStack *stack) { return stack->top == MAX_SIZE - 1;}// 入栈操作bool pushArrayStack(ArrayStack *stack, int value) { if (isArrayStackFull(stack)) { printf(\"栈已满，无法入栈！\\n\"); return false; } stack->data[++stack->top] = value; return true;}// 出栈操作bool popArrayStack(ArrayStack *stack, int *value) { if (isArrayStackEmpty(stack)) { printf(\"栈为空，无法出栈！\\n\"); return false; } *value = stack->data[stack->top--]; return true;}// 获取栈顶元素bool peekArrayStack(ArrayStack *stack, int *value) { if (isArrayStackEmpty(stack)) { printf(\"栈为空！\\n\"); return false; } *value = stack->data[stack->top]; return true;}// 打印栈内容void printArrayStack(ArrayStack *stack) { if (isArrayStackEmpty(stack)) { printf(\"栈为空！\\n\"); return; } printf(\"栈内容(从栈底到栈顶): \"); for (int i = 0; i top; i++) { printf(\"%d \", stack->data[i]); } printf(\"\\n\");}

链表实现（静态链表栈）

#include #include #define MAX_NODES 100 // 最大节点数// 链表节点结构typedef struct StackNode { int data; int next; // 使用数组下标代替指针} StackNode;// 链表实现的栈结构typedef struct { StackNode nodes[MAX_NODES]; // 节点池 int top;  // 栈顶节点下标 int freeList; // 空闲节点链表头 int size;  // 当前栈大小} LinkedStack;// 初始化栈void initLinkedStack(LinkedStack *stack) { stack->top = -1; // 空栈 stack->size = 0; // 初始化空闲链表 for (int i = 0; i nodes[i].next = i + 1; } stack->nodes[MAX_NODES - 1].next = -1; // 结束标记 stack->freeList = 0; // 第一个空闲节点}// 从空闲链表分配一个节点int allocateNode(LinkedStack *stack) { if (stack->freeList == -1) { return -1; // 没有空闲节点 } int nodeIndex = stack->freeList; stack->freeList = stack->nodes[nodeIndex].next; return nodeIndex;}// 释放节点到空闲链表void freeNode(LinkedStack *stack, int nodeIndex) { stack->nodes[nodeIndex].next = stack->freeList; stack->freeList = nodeIndex;}// 判断栈是否为空bool isLinkedStackEmpty(LinkedStack *stack) { return stack->top == -1;}// 判断栈是否已满bool isLinkedStackFull(LinkedStack *stack) { return stack->freeList == -1;}// 入栈操作bool pushLinkedStack(LinkedStack *stack, int value) { if (isLinkedStackFull(stack)) { printf(\"栈已满，无法入栈！\\n\"); return false; } int newNode = allocateNode(stack); stack->nodes[newNode].data = value; stack->nodes[newNode].next = stack->top; stack->top = newNode; stack->size++; return true;}// 出栈操作bool popLinkedStack(LinkedStack *stack, int *value) { if (isLinkedStackEmpty(stack)) { printf(\"栈为空，无法出栈！\\n\"); return false; } int topNode = stack->top; *value = stack->nodes[topNode].data; stack->top = stack->nodes[topNode].next; freeNode(stack, topNode); stack->size--; return true;}// 获取栈顶元素bool peekLinkedStack(LinkedStack *stack, int *value) { if (isLinkedStackEmpty(stack)) { printf(\"栈为空！\\n\"); return false; } *value = stack->nodes[stack->top].data; return true;}// 打印栈内容void printLinkedStack(LinkedStack *stack) { if (isLinkedStackEmpty(stack)) { printf(\"栈为空！\\n\"); return; } printf(\"栈内容(从栈顶到栈底): \"); int current = stack->top; while (current != -1) { printf(\"%d \", stack->nodes[current].data); current = stack->nodes[current].next; } printf(\"\\n\");}

这两种静态实现方式都不使用动态内存分配(malloc/free)，适合在资源受限的环境中使用，如嵌入式系统。 

推荐优先使用动态数组实现栈，除非：
1. 栈大小变化极其剧烈且不可预测
2. 元素非常大（移动成本高）
3. 有严格的无上限要求
动态数组实现提供了更好的综合性能，而现代内存分配器和扩容策略（如倍增法）已经大大减少了其缺点。在C语言中，通过合理的realloc策略可以实现高效的动态数组栈。

选择哪种实现取决于具体应用场景、性能要求和资源限制。在大多数现代应用中，动态实现更为常用，因为它提供了更大的灵活性。而在嵌入式系统或对性能有严格要求的场景中，静态实现可能更合适。下面我们来看一下动态实现栈：

3. 动态实现栈（数组）

 #include#include#include#include//基本操作： // 1.初始化// 2.销毁// 3.判空// 4.压栈// 5.出栈// 6.返回栈顶元素// 7.返回栈中元素个数 //用顺序表实现栈//栈的性质：后进先出 typedef int STDataType; typedef struct stack { STDataType* a;//指向栈底位置 int top;//已有栈顶元素的个数 int capacity;// 栈容量 }ST; //栈的初始化-- 和顺序表的一系列操作差不多 void STInit(ST* ps){assert(ps); ps->a = (STDataType*)malloc(sizeof(STDataType)*4);if(ps->a == NULL){perror(\"malloc fail\");return; } ps->capacity = 4;//初始化容量为4 ，不够再扩容//ps->top = 0;//top是栈顶元素下一个 ps->top = -1;//top是栈顶元素 }//栈的销毁 void STDestroy(ST* ps){assert(ps);free(ps->a);ps->a=NULL;ps->top=ps->capacity = 0;}//判空 bool STEmpty(ST* ps){assert(ps);return ps->a[ps->top] == 0;}void STPush(ST* ps, STDataType x){assert(ps);if(ps->top + 1 == ps->capacity){STDataType* tmp = (STDataType*)realloc(ps->a,sizeof(STDataType)*ps->capacity*2);if(tmp == NULL){perror(\"realloc fail\");return;}ps->a = tmp;ps->capacity *= 2; }ps->a[ps->top+1] = x;ps->top++;}//出栈 void STPop(ST* ps){assert(ps);assert(!STEmpty(ps));ps->top--;}//栈中元素个数 int STSize(ST* ps){assert(ps);return ps->top+1;}//栈顶元素 STDataType STTop(ST* ps){ assert(ps); assert(!STEmpty(ps)); return ps->a[ps->top];}int main(){ST st;STInit(&st);//初始化 //压栈-- 向栈中放入数据 STPush(&st,1); STPush(&st,2); STPush(&st,3); STPush(&st,4); STPush(&st,5); //取栈顶元素 //根据栈的性质 top == 5 // 打印出来看一下 printf(\"%d\\n\",STTop(&st)); //出栈--弹出栈顶元素 STPop(&st); STPop(&st); //Pop两次 -- 那么此时栈顶的元素应该为 3 //打印出来看一下 printf(\"%d\\n\",STTop(&st)); STPop(&st); //此时栈中应该只有两个元素了 //打印栈中元素的个数 printf(\"%d\\n\",STSize(&st)); //最终结果为 5 //  3 // 2 //销毁栈 STDestroy(&st); //以上为一个栈从创建到销毁的完整的过程 //能够完成栈的基本操作 return 0; }