【烧脑算法】矩形面积求解:从公式到代码的深度剖析
目录
前言
84. 柱状图中最大的矩形
1793. 好子数组的最大分数
85. 最大矩形
221. 最大正方形
42. 接雨水
1504. 统计全 1 子矩形
1277. 统计全为 1 的正方形子矩阵
总结
前言
求矩阵大小,矩阵数量,矩阵最大面积......这些在日常面试题中并不少见,所以有必要研究以下这种类型题目的解题思路和方向。关于矩阵类的题目我们最常用的工具就是:前缀和,单调栈,遍历数组。所以想要搞清楚矩形类题目的接替角度,就需要将这些工具灵活使用,以下将结合题目来剖析矩形类题目的出题角度和解题思路。
PS:本篇博客中的所有题目均来自于灵茶山艾府 - 力扣(LeetCode)分享的题单。
矩形题目
84. 柱状图中最大的矩形
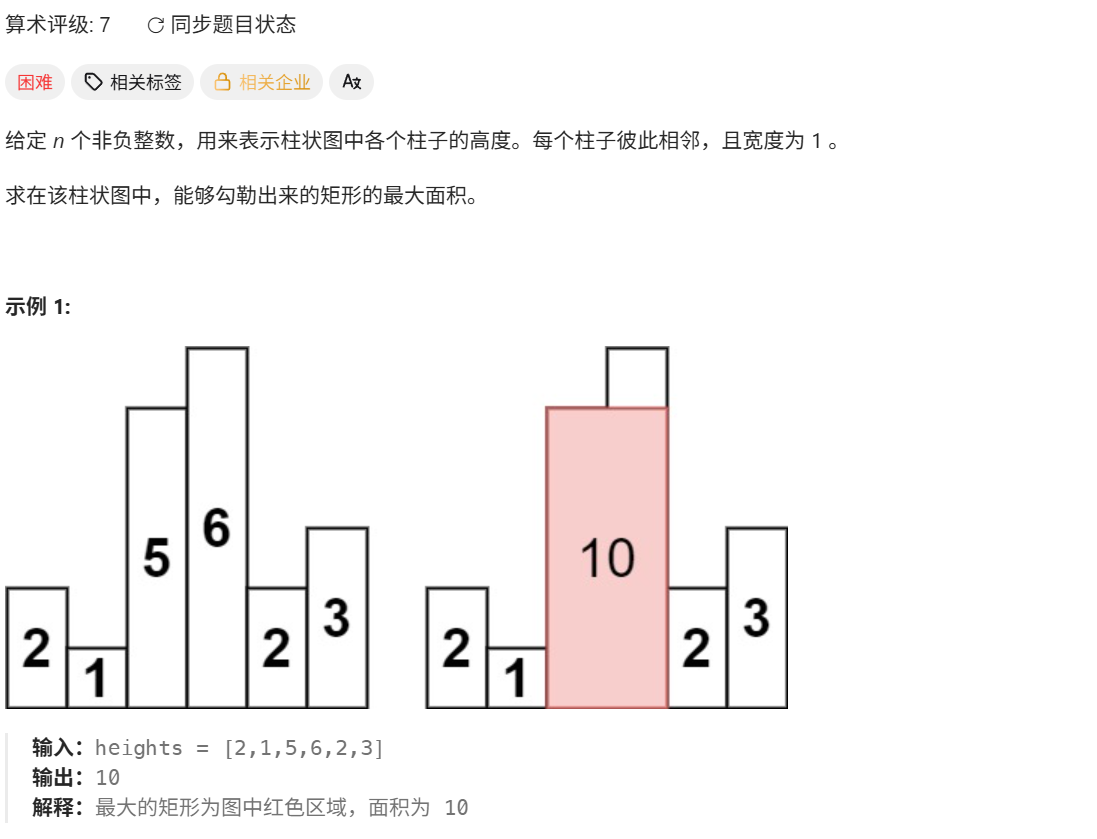
最大高度一定是heights中的一个元素(可以通过反证法推一下)。所以 以某一个元素作为最大元素时要找其左右的最大宽度,就需要向左向右找第一个小于该位置的下标。
使用三个循环来实现,前两个循环来找每个位置可以向左向右扩展的最大位置,最后一个循环进行统计。
class Solution {public: int largestRectangleArea(vector& nums) { //需要知道每一个位置向左向右的宽度 //使用两次单调栈来求最大宽度 int n=nums.size(); vector right(n,n); //right中存储扩展不了的位置 stack<pair> st; //存储还没有找到位置的元素大小以及下标 for(int i=0;inums[i]) { int index=st.top().second; right[index]=i; st.pop(); } st.push({nums[i],i}); } vector left(n,-1); //left中存储先做扩展不到的位置 while(!st.empty()) st.pop(); for(int i=n-1;i>=0;i--) { while(!st.empty()&&st.top().first>nums[i]) { int index=st.top().second; left[index]=i; st.pop(); } st.push({nums[i],i}); } int ret=0; for(int i=0;i<n;i++) ret=max(ret,nums[i]*(right[i]-left[i]-1)); return ret; }};1793. 好子数组的最大分数

此题可以说是上一题的简化,根据题目min(nums[i]......)*(j-i+1)这不就是矩形的面积吗,但是因为此题给出了k所以就没必要像上一题一样使用两次单调栈来完成。此题可以直接使用双指针从k位置开始向左右两边进行扩展。
题解:此题比较简单,可以使用双指针来完成;以下标为k的位置开始向左向右进行扩展,对左右进行比较向更大的一边扩,知道扩展完。
class Solution {public: int maximumScore(vector& nums, int k) { //使用双指针先左右两边依次扩展,对两边进行比较,先大的一边扩 int n=nums.size(); int left=k-1,right=k+1; int ret=nums[k],t=nums[k]; while(left>=0&&rightnums[right]) left--; //判断向左还是向右扩展 else right++; t=min({t,nums[left+1],nums[right-1]}); ret=max(ret,(right-left-1)*t); } while(left>=0) //保证向左扩展完 { t=min(t,nums[left--]); ret=max(ret,(right-left-1)*t); } while(right<n) //保证向右扩展完 { t=min(t,nums[right++]); ret=max(ret,(right-left-1)*t); } return ret; }};85. 最大矩形

与上面的第一个题一样。此题可以模拟上面以题的解法,对矩一列一列的处理,依次向下走。每一次都重新统计1的长度,将每一列1的长度存储起来就可以直接调用第84题的代码了。
class Solution {public: int maximalRectangle(vector<vector>& matrix) { int m=matrix.size(),n=matrix[0].size(); auto r_max=[&](int level) { vector nums(n); //统计从level层开始向下连续1的长度 for(int i=0;i<n;i++) { int j=level; while(j<m&&matrix[j][i]==\'1\') j++; nums[i]=j-level; } //以下与84题代码一样 //向左向右统计可以扩展的最大长度 vector right(n,n); stack<pair> st; for(int i=0;inums[i]) { int index=st.top().second; right[index]=i; st.pop(); } st.push({nums[i],i}); } while(!st.empty()) st.pop(); vector left(n,-1); for(int i=n-1;i>=0;i--) { while(!st.empty()&&st.top().first>nums[i]) { int index=st.top().second; left[index]=i; st.pop(); } st.push({nums[i],i}); } int each=0; for(int i=0;i<n;i++) each=max(each,(right[i]-left[i]-1)*nums[i]); return each; }; int ret=0; for(int k=0;k<m;k++) //对每一层都进行统计 ret=max(ret,r_max(k)); return ret; }};221. 最大正方形
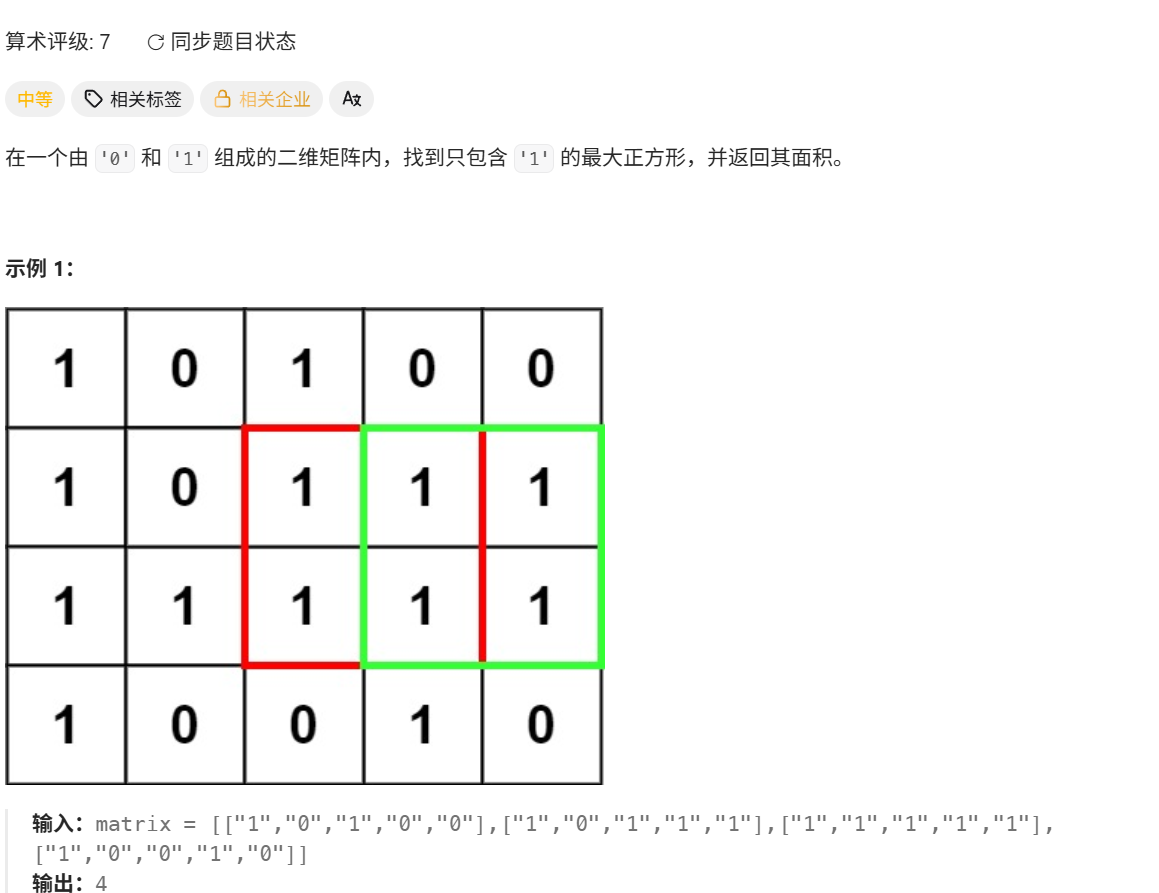
上一题的一个拓展,与上一题的不同在于此题要求找的是正方形而不是长方形,在上面代码的基础上增加一步:判断长和宽的大小选择小的哪一个。
class Solution {public: int maximalSquare(vector<vector>& matrix) { int m=matrix.size(),n=matrix[0].size(); auto r_max=[&](int level) { vector nums(n); //统计从level层开始向下连续1的长度 for(int i=0;i<n;i++) { int j=level; while(j<m&&matrix[j][i]==\'1\') j++; nums[i]=j-level; } //以下与84题代码一样 //向左向右统计可以扩展的最大长度 vector right(n,n); stack<pair> st; for(int i=0;inums[i]) { int index=st.top().second; right[index]=i; st.pop(); } st.push({nums[i],i}); } while(!st.empty()) st.pop(); vector left(n,-1); for(int i=n-1;i>=0;i--) { while(!st.empty()&&st.top().first>nums[i]) { int index=st.top().second; left[index]=i; st.pop(); } st.push({nums[i],i}); } int each=0; for(int i=0;i<n;i++) { int len=min(right[i]-left[i]-1,nums[i]); //选取长和宽中小的哪一个 each=max(each,len*len); } return each; }; int ret=0; for(int k=0;k<m;k++) //对每一层都进行统计 ret=max(ret,r_max(k)); return ret; }};42. 接雨水

接雨水问题很经典的一道题,使用两次前缀和即可。
使用前缀和,从左到右和从右到左:
- 从左到右:假设右边的柱子无限高,看当前这个位置雨水的高度
- 从右向左:假设左边的柱子无限高,看当前这个位置雨水的高度
- 因为柱子不一定是无限高,所以不一定满足条件
- 但是此时right和left数组中已经存储了从左向右和从右向左可以达到的高度,取两者的较小值就是水面的高度
class Solution {public: int trap(vector& nums) { //使用前缀和,从左到右和从右到左 //从左到右:假设右边的柱子无限高,看当前这个位置雨水的高度 //从右向左:假设左边的柱子无限高,看当前这个位置雨水的高度 int n=nums.size(); vector left(n); //此处可以不使用单调栈,直接记录已经遍历部分柱子的最大值即可 int len=0; for(int i=0;i<n;i++) { len=max(len,nums[i]); left[i]=len; } len=0; vector right(n); for(int i=n-1;i>=0;i--) { len=max(len,nums[i]); right[i]=len; } //因为柱子不一定是无限高,所以不一定满足条件, //但是此时right和left数组中已经存储了从左向右和从右向左可以达到的高度,取两者的较小值就是水面的高度 int ret=0; for(int i=0;i<n;i++) { ret+=min(right[i],left[i])-nums[i]; } return ret; }};1504. 统计全 1 子矩形

便往前走,便往回看。枚举从0-n的每一个位置作为右边界,向前找左边界。
- 一层层的处理,从左到右统计每一列连续1的个数;
- 枚举每一个位置作为右边界,向右走;
- 回头看有多少个满足条件的左边界。
class Solution {public: int numSubmat(vector<vector>& matrix) { int m=matrix.size(),n=matrix[0].size(); auto r_max=[&](int level) { vector nums(n); //统计从level层开始向下连续1的长度 for(int i=0;i<n;i++) { int j=level; while(j<m&&matrix[j][i]==1) j++; nums[i]=j-level; } //使用一个栈记录前面的位置的高度 int each=0; for(int i=0;i=0;j--) { l=min(nums[j],l); each+=l; } } return each; }; int ret=0; for(int k=0;k<m;k++) //对每一层都进行统计 ret+=r_max(k); return ret; }};1277. 统计全为 1 的正方形子矩阵

上面一题的变形,在得到矩阵之后变成正方形即可。
class Solution {public: int countSquares(vector<vector>& matrix) { int m=matrix.size(),n=matrix[0].size(); auto r_max=[&](int level) { vector nums(n); //统计从level层开始向下连续1的长度 for(int i=0;i<n;i++) { int j=level; while(j<m&&matrix[j][i]==1) j++; nums[i]=j-level; } //使用一个栈记录前面的位置的高度 int each=0; for(int i=0;i=0;j--) { l=min(l,nums[j]); if(l>=i-j+1) each++; else break; } } return each; }; int ret=0; for(int k=0;k<m;k++) //对每一层都进行统计 ret+=r_max(k); return ret; }};总结
矩形类题目,通常都是vector<vector>类型的,所以有时需要分层处理,依次求解。这类题目的解题套路是很固定的,只需要记住上面的解题套路即可,多加注意一些细节,边界问题...


