第二十七届华东杯数学建模A 题 跳台滑雪问题 完整思路模型及代码_数学建模 跳台滑雪

题目背景

跳台滑雪起源于 19 世纪，是冬季运动会的传统竞技项目。今年亚洲冬季运动会在我国

哈尔滨举行，跳台滑雪项目吸引了包括中国在内的亚洲各国运动健儿踊跃参加，我国运动员取得了优异的成绩。

跳台滑雪融合了速度、力量与精确控制，展现出运动员在高空飞跃中的技巧与勇气，是冬季运动中最具观赏性的项目之一。运动员在完成过程中，不同的身体姿态对最终得分有很大影响，分析各阶段运动员应采取怎样的姿态能够提高运动成绩。

跳台滑雪的比赛场地通常由出发台、助滑坡、起跳台、着陆坡和终止区组成，如下图所示。跳台滑雪的技术可分解为助滑与起跳、空中飞行、着陆和终止滑行 4 个阶段。

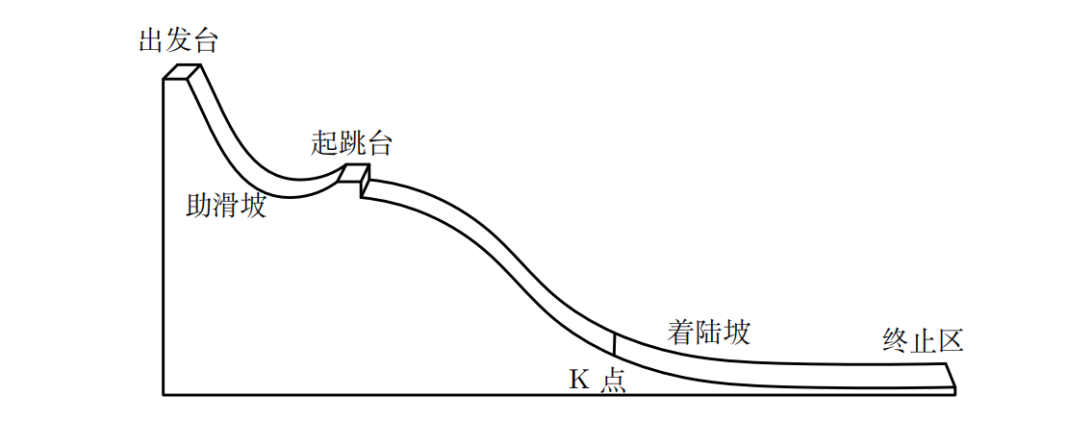
跳台滑雪的评分标准由距离分和姿势分组成，并结合赛道参数计算总分（附录 A）。

请建立数学模型，解决以下问题，并根据附录 B 提供的赛道数据给出计算结果。

解题摘要

针对问题一，我们建立了助滑阶段空气动力学模型。考虑到滑行过程中的空气阻力和摩擦力对速度的影响，我们引入了不同姿态下运动员迎风面积和空气阻力系数的变化，利用牛顿第二定律建立加速度表达式，并通过数值模拟比较常见姿态下的终端速度。结果表明，运动员应采取低蹲前倾姿势，以降低迎风面积和阻力系数，从而获得最大的起跳速度。

针对问题二，我们构建了二维空中飞行动力学模型，结合起跳速度、身体迎角、滑雪板倾角等因素，模拟运动员在空中飞行的轨迹与姿态变化，采用欧拉法对运动过程进行仿真，优化飞行路径和稳定性。仿真结果表明，运动员应在起跳后保持滑雪板与身体成“V”字形打开、重心略后倾的姿态，以增强升力、延长飞行距离并提高姿态得分。

针对问题三，我们基于力学平衡条件建立了着陆平衡模型，引入重心位置、着陆角度、风速与反应延迟等变量构建稳定性评分函数，并使用Python对着陆过程进行热力图仿真。结果显示，运动员在着陆时应保持重心尽量居中、着陆角接近坡面角度（约34°），并提前调节姿态以补偿神经反应延迟，以实现最佳平衡状态并避免扣分。

问题一

 运动员在助滑坡应采取何种姿势，以获得较大的起跳速度？

我们可以为跳台滑雪的全过程建立一个完整的三阶段数学模型（助滑 + 飞行 + 着陆），并模拟出跳跃的轨迹和最终得分。

阶段一：助滑 + 起跳

模拟从高处加速下滑过程，计算到达起跳台末端的速度。

起跳点速度作为飞行初速度输入。

阶段二：空中飞行

建立包含重力和空气动力的二维运动模型（含升力和阻力）。

模拟运动员在空中轨迹，计算水平飞行距离。

阶段三：着陆判定与得分

根据飞行距离判断是否落在 K 点前/后。

计算距离分、姿势分（设定规则或模拟不同落地情况）、风速补偿（设为固定值或函数）。

输出总得分。

所需参数设置（参考附录 B 和物理常数）

参数

数值

说明

重力加速度 ggg

9.81 m/s²

常数

空气密度 ρ\\rhoρ

1.225 kg/m³

海平面

阻力系数 CD

0.4（助滑）/ 0.6（飞行）

姿势相关

升力系数 CL

0.3–0.6（飞行）

滑雪板迎角决定

迎风面积 AAA

0.4–0.6 m²

姿势紧缩与否

运动员质量 mmm

70 kg

助滑坡倾角 θ1\\theta_1θ1​

35°

自定义或参考赛道图

起跳角度 θ2\\theta_2θ2​

11°

范围10°–12°

飞行起跳点高度 h0h_0h0​

60 m

落差约60米

起跳到着陆坡水平距离

140 m

K 点位置

120 m

代码如下

#完整↓#关zhu：数模Lab#回复1