网站导航
> 技术文档 > CUDA实现并行矩阵乘gemm_cuda gemm

CUDA实现并行矩阵乘gemm_cuda gemm

网友: 技术文档 2025-07-30 11:22:45

CUDA实现GEMM

  • 原始实现
  • 线程块tile和共享内存优化
  • 线程tile优化
  • 矩阵转置
  • 向量化访存
  • double buffer
  • 最终版本代码

顾名思义，两个矩阵相乘

原始实现

使用M*N个线程
每个线程计算C中的一个元素：读一行、一列（没有依赖）
二维线程组织映射到矩阵元素
单个线程块计算
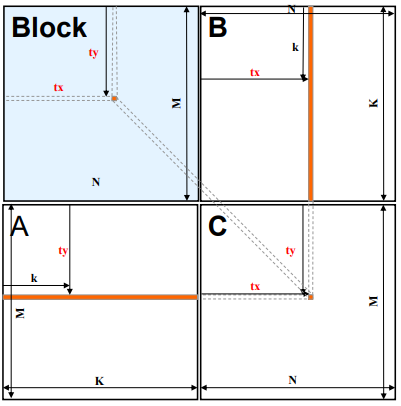
CUDA实现并行矩阵乘gemm_cuda gemm
代码实现相对简单：

__global__ void SGEMMBlockKernel(float *A, float *B, float *C, int M, int N, int K){ float tmp = 0.0; int tx = threadIdx.x , ty = threadIdx.y; for(int i = 0; i < K; i++) { tmp += A[ty * K + i] * B[i * N + tx]; } C[ty * N + tx] = tmp; }

上述原始实现的计算访存比是很低的。
每一次乘加计算：访存两次，FFMA一次
优化思路：
1，从全局内存中取数据可能要几百个时钟周期，而从共享内存里取更低一些，所以可以看看数据能不能放到共享内存中。
2，cuda线程涉及到的线程上下文切换主要是通过保存和恢复线程的寄存器状态实现的，延迟很低，可以看作是0开销，所以可以让线程去干点别的，等待访存，从而隐藏延迟。

线程块tile和共享内存优化

优化思路如下：

  • 每个线程计算C中的一个元素
  • 同一行线程读取A中一行数据
  • 同一列线程读取B中一列数据
  • 将block共享的数据放到shared memory上

如下图：
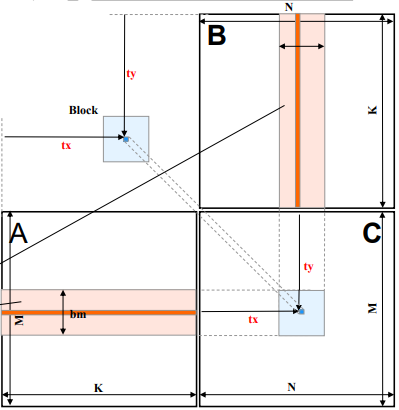
CUDA实现并行矩阵乘gemm_cuda gemm
但是，共享内存通常不会很大，共享内存可能放不下需要共享的数据。
所以我们使用线程块tile的思想。

  • 使用2维网格，2维线程块
  • 每个线程块计算C中的一块（一个tile）
  • 每个线程块迭代取绿色块到共享内存中相乘
  • 迭代结果累加
  • 每个线程计算C中的一个元素
    如下图：
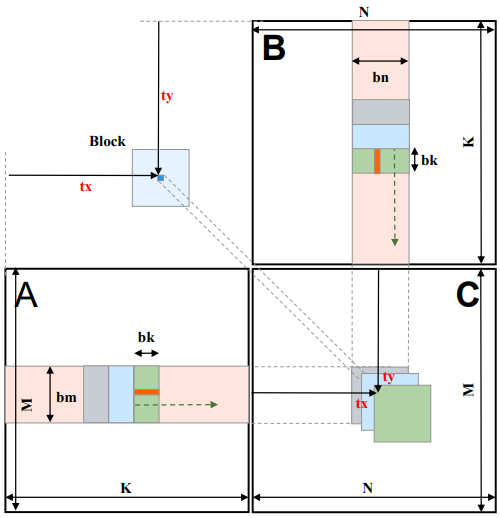
    CUDA实现并行矩阵乘gemm_cuda gemm
    代码实现：
    我们使用template增强函数的通用性。
template < const int BLOCK_SIZE_M, const int BLOCK_SIZE_K, const int BLOCK_SIZE_N > __global__ void SGEMMBlockTileKernal(float *A, float *B, float *C, int M, int N, int K){ __shared__ float As[BLOCK_SIZE_M][BLOCK_SIZE_K]; __shared__ float Bs[BLOCK_SIZE_K][BLOCK_SIZE_N]; int ty = blockIdx.y * BLOCK_SIZE_M + threadIdx.y; int tx = blockIdx.x * BLOCK_SIZE_N + threadIdx.x; if (tx < M && ty < N) { float tmp = 0.0; for (int i = 0; i < (K / BLOCK_SIZE_K); i++) { As[threadIdx.y][threadIdx.x] = A[ty * K + (i * BLOCK_SIZE_K + threadIdx.x)]; Bs[threadIdx.y][threadIdx.x] = B[tx + (i * BLOCK_SIZE_K + threadIdx.y) * N]; __syncthreads(); for (int k = 0; k < BLOCK_SIZE_K; k++) tmp += As[threadIdx.y][k] * Bs[k][threadIdx.x]; __syncthreads(); } C[ty * N + tx] = tmp; }}

对上述代码进行性能分析：
-线程块tile之前：访存总次数2MNK。
-线程块tile后：总迭代次数：M/bm * N/bn * K/bk。
-每次迭代读取A中bmbk，B中bk*bn，访存总次数：

  • M/bm * N/bn * K/bk *（bm * bk + bk * bn）=
    M * N * K * (1/bm + 1/bn)

访存量变成原来的1/2 * (1/bm + 1/bn)
更充分的利用了数据局部性。

线程tile优化

上面优化我们发现，随着bm和bn的增加，访存量也按比例缩小
但是，线程块不能太大，占用共享内存过多的话，会导致SM上活跃的warp变少，不能很好的完成延迟隐藏。
另外，计算访存比仍然是=1：2。
有了线程块的tile，我们还可以给线程tile：
• 对𝑏𝑚 ∗ 𝑏𝑛划分成𝑟𝑚 ∗ 𝑟𝑛的子矩阵
• 一共𝑏𝑚/𝑟𝑚 * 𝑏𝑛/𝑟𝑛 个子矩阵
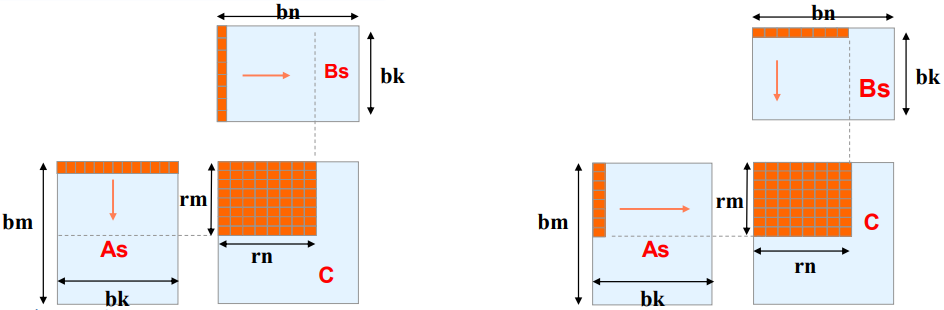
CUDA实现并行矩阵乘gemm_cuda gemm
如上图，内积和外积都可以完成矩阵运算，但是
内积实现：

for i from 0 to rm:for j from 0 to rn:for k from 0 to bk:C[i][j] += As[i][k] * Bs[k][j];

外积实现：

for k from 0 to bk:for i from 0 to rm:for j from 0 to rn:C[i][j] += As[i][k] * Bs[k][j];

先看内积：
计算每个ij位置的元素需要取访存两次，计算一次，计算访存比为1：2。
而且，As中的每一行和Bs中的每一列是会被重复读取的。
访存次数为rm * rn * 2
外积：
每次取两个向量（假设长度为8），就先进行8*8次计算，不存在重复读取的情况，因为外积中每一行和每一列计算完后就不需要了，访存次数为rm+rn。计算访存比为64：16=4
而且k固定后，可以直接把Bs那一行都存到寄存器中，ki固定后，可以把As那一个元素存到寄存器中，这就需要rn+1个寄存器，总共64个元素，每次又需要8+8个寄存器，所以总共寄存器需要80个寄存器。所以这是一种用高级存储换低级存储的方法。

每个线程负责rm * rn 个元素的计算
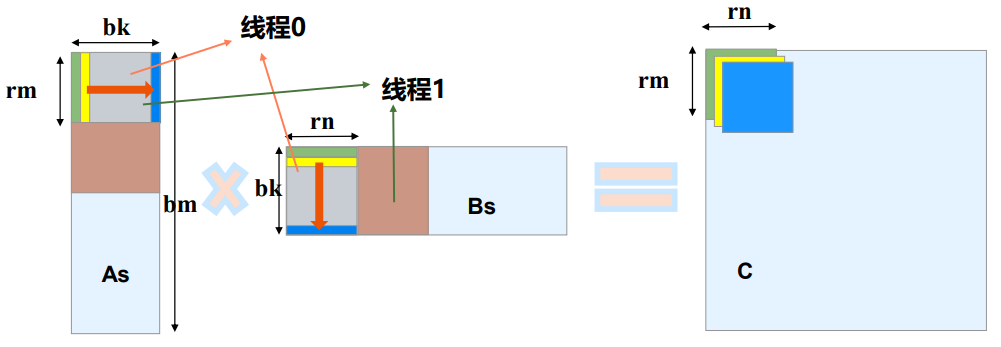
CUDA实现并行矩阵乘gemm_cuda gemm
如何选择bm bn bk rm rn？
rm rn 越大，按理来说，计算访存比就会越高，优化越好，但是占用寄存器也会越多。寄存器用的多，会导致一个SM中能承载的warp变少，会影响一个指标：占用率occupancy，即warp数/SM中最大的warp数，占用率越低说明可供gpu进行线程切换的warp越少。

线程tile优化分析
因为线程块tile没变，所以我们只分析线程块内的。
对共享内存访存减少了多少？

  • 线程tile之前，线程块访存次数 2 ∗ 𝑏𝑚 ∗ 𝑏𝑛 ∗ 𝑏𝑘
  • 线程tile之后，有𝑏𝑚/𝑟𝑚 ∗ 𝑏𝑛/𝑟n个线程，访存次数
    𝑏𝑚/𝑟𝑚 ∗ 𝑏𝑛/𝑟𝑛 ∗ （𝑟𝑚 + 𝑟𝑛） ∗ 𝑏𝑘 = 𝑏𝑚 ∗ 𝑏𝑛 ∗ 𝑏𝑘 ∗ (1/𝑟𝑚+1/𝑟𝑛)
  • 访存量变成原来的1/2 ∗ (1/𝑟𝑚 + 1/𝑟𝑛)

另外，因为我们在循环中把数据放到了寄存器中，所以，也能减少从共享内存中取数据的延迟。

矩阵转置

As的访问是不连续的。
所以如果我们把As转置的话，就可以连续访问了。
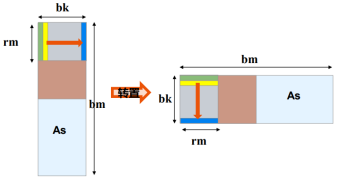
CUDA实现并行矩阵乘gemm_cuda gemm

向量化访存

Cuda存在一种优化技术：合并访存（Memory Coalescing），将多个线程的连续内存地址访问合并为1个，从而减轻对内存控制器的压力。
如下图：如果一个线程需要访问2次每次获取4byte数据，那么一个warp就有32*2=64次访问，会被合并成8次访问。
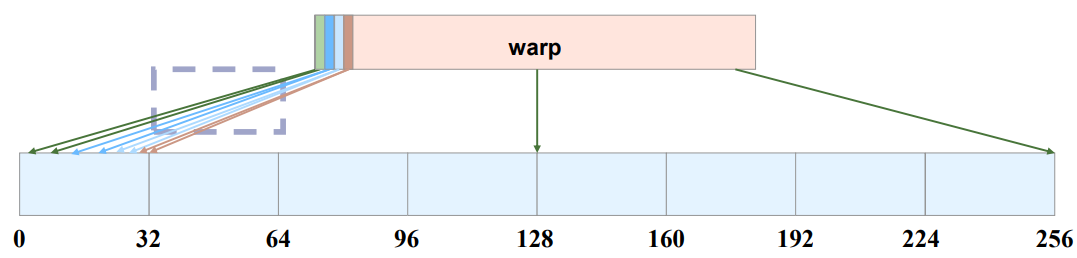
CUDA实现并行矩阵乘gemm_cuda gemm
如果使用了向量化访存，将2次4 byte的访问合并成一次8byte的访问的话，仍然是被合并成8次访问，不过聚合访问本身的压力就低了。
Cuda目前大致支持128bit的向量化访存，也就是float4，这是一个cuda独有的数据类型，表示4个float。
另外，bm、bn、bk、rm、rn要与向量化对齐。
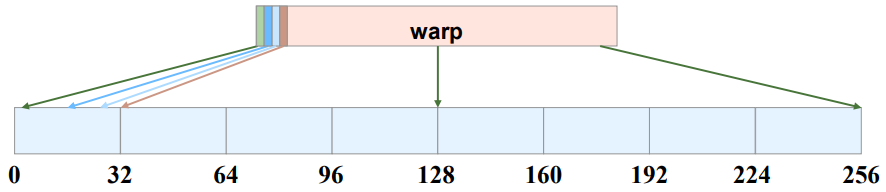
CUDA实现并行矩阵乘gemm_cuda gemm
我们可以使用宏定义完成指针的转换：

#define FETCH_FLOAT4(pointer) (reinterpret_cast<float4*>(&(pointer))[0])

double buffer

实现读写分离，多个步骤的流水并行。

在CUDA编程中，某些GPU架构在将数据从全局内存复制到共享内存时，确实需要经过寄存器。这种情况通常发生在较早的GPU架构上，例如Fermi架构（Compute Capability 2.x）及之前的架构。在这些架构中，数据从全局内存到共享内存的传输可能需要通过寄存器进行中转，以便在内核执行时进行处理。这种设计可能会导致性能瓶颈，因为寄存器的数量是有限的，并且寄存器的访问速度通常比共享内存慢。然而，在较新的GPU架构（如Kepler及之后的架构）中，数据传输的效率得到了显著改善，通常可以直接在全局内存和共享内存之间进行传输，而不需要经过寄存器。这使得数据传输的性能得到了提升。

如下图：
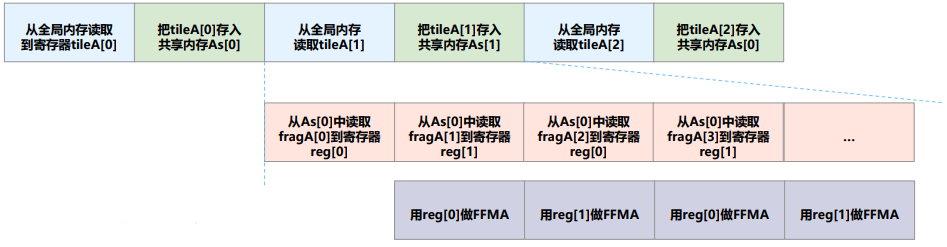
CUDA实现并行矩阵乘gemm_cuda gemm
请注意：double buffer 最好最后去作优化，因为需要修改的代码很多。

最终版本代码

上述优化思路结合其实是一个大迭代套小迭代的过程。
很复杂，画个图会清晰很多。
假设我们的运算是：
矩阵A（MN）乘以矩阵B（KN）得到矩阵C（M*N）
我们的bm和bn采用128，bk采用8，rm和rn选用8。

//计算位于矩阵（行优先）里第row行，第col列的元素的全局索引，ld是矩阵的宽度#define OFFSET(row, col, ld) ((row) * (ld) + (col))// 按照float4去取#define FETCH_FLOAT4(pointer) (reinterpret_cast<float4*>(&(pointer))[0])template < const int BLOCK_SIZE_M, // 单个线程块计算A的高度 const int BLOCK_SIZE_K, // 单个线程块单轮迭代计算的A的宽度，B的高度 const int BLOCK_SIZE_N, // 单个线程块计算B的宽度 const int THREAD_SIZE_Y, // 单个线程计算的高度（结果矩阵C） const int THREAD_SIZE_X // 单个线程计算的宽度（结果矩阵C） > __global__ void SGEMMBestKernal( float * __restrict__ A, float * __restrict__ B, float * __restrict__ C, const int M, const int N, const int K) { // 线程块索引 int bx = blockIdx.x; // 横向的block坐标 int by = blockIdx.y; // 纵向的block坐标 // 块内线程索引 int tx = threadIdx.x; // 横向的线程坐标 int ty = threadIdx.y; // 纵向的线程坐标 // 块内线程的长度，高度和总数 const int THREAD_X_PER_BLOCK = BLOCK_SIZE_N / THREAD_SIZE_X; // 线程块中每一行128/8=16个线程 const int THREAD_Y_PER_BLOCK = BLOCK_SIZE_M / THREAD_SIZE_Y; // 线程块中每一列128/8=16个线程 const int THREAD_NUM_PER_BLOCK = THREAD_X_PER_BLOCK * THREAD_Y_PER_BLOCK; // 线程块中的线程总个数256个 // 当前的块内线程序号id，按行优先计算 const int tid = ty * THREAD_X_PER_BLOCK + tx; // double buffer // As: 存储A矩阵数据的共享内存，包含线程块单轮大迭代所需要的所有数据 __shared__ float As[2][BLOCK_SIZE_K][BLOCK_SIZE_M]; // Bs：存储B矩阵数据的共享内存，包含线程块单轮大迭代所需要的所有数据。不需要转置 __shared__ float Bs[2][BLOCK_SIZE_K][BLOCK_SIZE_N]; // // accum：临时存储单个线程中C的计算结果，方便FFMA指令累加。需要初始化为0 float tmpC[THREAD_SIZE_Y][THREAD_SIZE_X] = {0}; // 线程从A读的一列数据（转置后其实是从As中读的一行），长度是THREAD_SIZE_Y float tmpA[2][THREAD_SIZE_Y]; // 线程从Bs读的一行，长度是THREAD_SIZE_X float tmpB[2][THREAD_SIZE_X]; // a_load_count：单线程搬运单轮大迭代所有矩阵A数据的次数=线程块tile的As的数据个数 / (线程块内线程个数 * 4) // b_load_count：单线程搬运单轮大迭代所有矩阵B数据的次数=线程块tile的Bs的数据个数 / (线程块内线程个数 * 4) const int a_load_count = BLOCK_SIZE_M * BLOCK_SIZE_K / (THREAD_NUM_PER_BLOCK * 4); const int b_load_count = BLOCK_SIZE_K * BLOCK_SIZE_N / (THREAD_NUM_PER_BLOCK * 4); // 每一次搬运4个float数据，搬运次数 * 4 就是搬运对应数据需要的寄存器空间。 float load_global_a[4 * a_load_count]; float load_global_b[4 * b_load_count]; // 搬运一行A数据需要使用多少个线程，当bk = 8的时候，为了搬运A的一行，需要使用2个线程。 const int A_TILE_THREAD_PER_ROW = BLOCK_SIZE_K / 4; // 搬运一行B数据需要使用多少个线程，当bn = 128的时候， 为了搬运B的一行，需要使用128/4 = 32个线程。 const int B_TILE_THREAD_PER_ROW = BLOCK_SIZE_N / 4;//线程搬运As和Bs的时候的起始行数和列数const int A_TILE_ROW_START = tid / A_TILE_THREAD_PER_ROW; const int A_TILE_COL_START = tid % A_TILE_THREAD_PER_ROW * 4; const int B_TILE_ROW_START = tid / B_TILE_THREAD_PER_ROW; const int B_TILE_COL_START = tid % B_TILE_THREAD_PER_ROW * 4;// 搬运A数据需要跨越的行。一般情况下不需要跨步就能搬完，假定有16*16=256个线程，一行由2个线程搬运，一轮迭代可以搬运256/2=128行的数据。 // 如果只有8*8=64个线程，一轮迭代只能搬运64/2 = 32个数据，此时跨步为32，需要4抡迭代。//防止线程不够的操作，其实定义的是正好的。 const int A_TILE_ROW_STRIDE = THREAD_NUM_PER_BLOCK / A_TILE_THREAD_PER_ROW; //256 / 2 = 128 // 搬运B数据需要跨越的行。分析过程与A类似。 const int B_TILE_ROW_STRIDE = THREAD_NUM_PER_BLOCK / B_TILE_THREAD_PER_ROW;//改变当前线程块在A、B矩阵上的偏移，方便计算下标 A = &A[(BLOCK_SIZE_M * by)* K]; B = &B[BLOCK_SIZE_N * bx];//fermi架构及其之前的机构在将数据从全局内存复制到共享内存时，需要经过寄存器，在较新的架构里可以删掉。/*--------------大迭代前预取数据---------------*/#pragma unroll for ( int i = 0 ; i < BLOCK_SIZE_M ; i += A_TILE_ROW_STRIDE) { // load_global_idx是当前线程从全局内存获取数据的寄存器地址偏移，每个跨步内本线程读取4个数据 int load_global_idx = i / A_TILE_ROW_STRIDE * 4; FETCH_FLOAT4(load_global_a[load_global_idx]) = FETCH_FLOAT4(A[OFFSET( A_TILE_ROW_START + i, A_TILE_COL_START, K )]); // 注意放的是转置的位置，使用寄存器可以避免多次读取全局内存，因为存储后的索引不连续，没有办法使用FETCH_FLOAT4直接读取。 As[0][A_TILE_COL_START][A_TILE_ROW_START + i]=load_global_a[load_global_idx]; As[0][A_TILE_COL_START+1][A_TILE_ROW_START + i]=load_global_a[load_global_idx+1]; As[0][A_TILE_COL_START+2][A_TILE_ROW_START + i]=load_global_a[load_global_idx+2]; As[0][A_TILE_COL_START+3][A_TILE_ROW_START + i]=load_global_a[load_global_idx+3]; } // 读取B矩阵数据，因为不用转置，所以直接按行取，按行存。 #pragma unroll for ( int i = 0 ; i < BLOCK_SIZE_K; i += B_TILE_ROW_STRIDE) { FETCH_FLOAT4(Bs[0][B_TILE_ROW_START + i][B_TILE_COL_START]) = FETCH_FLOAT4(B[OFFSET( B_TILE_ROW_START + i, // row B_TILE_COL_START, // col N )]); } __syncthreads();//第一轮大迭代中第一轮小迭代的数据预取到寄存器 #pragma unroll for (int i = 0; i < THREAD_SIZE_Y; i += 4) { FETCH_FLOAT4(tmpA[0][i]) = FETCH_FLOAT4(As[0][0][THREAD_SIZE_Y * ty + i]); } #pragma unroll for (int i = 0; i < THREAD_SIZE_X; i += 4) { FETCH_FLOAT4(tmpB[0][i]) = FETCH_FLOAT4(Bs[0][0][THREAD_SIZE_X * tx + i]); }int share_write_flag = 1; // 对As[share_write_flag]进行写 int tile_idx = 0; // 代表大迭代时，在A矩阵的起始列号，每一次大迭代要读取BLOCK_SIZE_K列，直到完成大迭代，即tile_start_idx=K为止。 while(tile_idx < K){ tile_idx += BLOCK_SIZE_K; // 每次加上bk的长度 // 从全局内存预取下一次大迭代的数据过程，与上述预取第一轮大迭代所需数据的过程类似 // 之前读取全局内存B中数据时没有经过寄存器，因为不用转置。这里为了提高并行性需要分步骤读取，所以统一由寄存器中转 #pragma unroll for (int i = 0 ; i < BLOCK_SIZE_M ; i += A_TILE_ROW_STRIDE) { int load_global_idx = i / A_TILE_ROW_STRIDE * 4; FETCH_FLOAT4(load_global_a[load_global_idx]) = FETCH_FLOAT4(A[OFFSET( A_TILE_ROW_START + i, // row A_TILE_COL_START + tile_idx, // col K )]); } #pragma unroll for (int i = 0 ; i < BLOCK_SIZE_K; i += B_TILE_ROW_STRIDE) { int load_global_idx = i / B_TILE_ROW_STRIDE * 4; FETCH_FLOAT4(load_global_b[load_global_idx]) = FETCH_FLOAT4(B[OFFSET( tile_idx + B_TILE_ROW_START + i, // row B_TILE_COL_START, // col N )]); } int share_read_flag = share_write_flag ^ 1; // 读缓冲的序号，这个和write_idx对应，两者保持二进制位相反即可。 /*---------------小迭代---------------*/ /* 然后是BLOCK_SIZE_K-1次小迭代。按照前面的参数配置，在这里完成7次小迭代。 由于在小迭代中也采用了双缓冲的方式，需要将下一轮小迭代的数据提前写入到寄存器中，这个过程需要访问共享内存，会稍微慢点。 为了使得最后一轮小迭代计算与下一轮大迭代的第一次小迭代并行，所以这里循环没有计算最后一轮小迭代。 */ #pragma unroll for(int j = 0; j < BLOCK_SIZE_K - 1; ++j){ //7次迭代， // 第一步：这里从共享内存获取本线程下一轮小迭代计算所需要的值，存入寄存器 // 注意读写缓冲区的标识区别 #pragma unroll for (int i = 0; i < THREAD_SIZE_Y; i += 4) {  FETCH_FLOAT4(tmpA[(j+1)%2][i]) = FETCH_FLOAT4(As[share_read_flag][j+1][THREAD_SIZE_Y * ty + i]); } #pragma unroll for (int i = 0; i < THREAD_SIZE_X; i += 4) {  FETCH_FLOAT4(tmpB[(j+1)%2][i]) = FETCH_FLOAT4(Bs[share_read_flag][j+1][THREAD_SIZE_X * tx + i]); } //完成向量相乘 #pragma unroll for (int ia = 0; ia < THREAD_SIZE_Y; ia++) {  #pragma unroll for (int ib = 0; ib < THREAD_SIZE_X; ib++) { tmpC[ia][ib] += tmpA[j % 2][ia] * tmpB[j % 2][ib]; } } } // 之前从全局内存取到了寄存器，现在从寄存器存到As和Bs共享内存中，注意As是转置。 #pragma unroll for ( int i = 0 ; i < BLOCK_SIZE_M ; i += A_TILE_ROW_STRIDE) { int load_global_idx = i / A_TILE_ROW_STRIDE * 4;As[share_write_flag][A_TILE_COL_START][A_TILE_ROW_START + i]=load_global_a[load_global_idx]; As[share_write_flag][A_TILE_COL_START+1][A_TILE_ROW_START + i]=load_global_a[load_global_idx+1]; As[share_write_flag][A_TILE_COL_START+2][A_TILE_ROW_START + i]=load_global_a[load_global_idx+2]; As[share_write_flag][A_TILE_COL_START+3][A_TILE_ROW_START + i]=load_global_a[load_global_idx+3]; } // 每个线程从存储B数据的寄存器中取数到共享内存中，放到写缓冲区write SM中 #pragma unroll for ( int i = 0 ; i < BLOCK_SIZE_K; i += B_TILE_ROW_STRIDE) { int load_global_idx = i / B_TILE_ROW_STRIDE * 4;  FETCH_FLOAT4(Bs[share_write_flag][B_TILE_ROW_START + i][B_TILE_COL_START]) = FETCH_FLOAT4(load_global_b[load_global_idx]); } __syncthreads(); // 从共享内存中预取下一轮大迭代第一次小迭代的数据，因为大迭代不同，所以要单独处理。 // 预取过程与上述类似，获取tile中的A的一列8X1，然后存入寄存器中。 #pragma unroll for (int i = 0; i < THREAD_SIZE_Y; i += 4) { FETCH_FLOAT4(tmpA[0][i]) = FETCH_FLOAT4(As[share_read_flag^1][0][THREAD_SIZE_Y * ty + i]); } #pragma unroll for (int i = 0; i < THREAD_SIZE_X; i += 4) { FETCH_FLOAT4(tmpB[0][i]) = FETCH_FLOAT4(Bs[share_read_flag^1][0][THREAD_SIZE_X * tx + i]); } #pragma unroll for (int ia = 0; ia < THREAD_SIZE_Y; ia++) { #pragma unroll for (int ib = 0; ib < THREAD_SIZE_X; ib++) { tmpC[ia][ib] += tmpA[1][ia] * tmpB[1][ib]; } } // 读写缓冲区交换 share_write_flag ^= 1; } // 当前线程负责的C中矩阵8X8小块的计算，已经全部计算完毕，并且结果已经被存储在accum寄存器中 // 需要将寄存器中的结果写回到全局内存C中。 #pragma unroll for (int i = 0; i < THREAD_SIZE_Y; ++i) { #pragma unroll for (int j = 0; j < THREAD_SIZE_X; j+=4) { // 注意C大矩阵的偏移计算。 FETCH_FLOAT4(C[OFFSET( BLOCK_SIZE_M * by + ty * THREAD_SIZE_Y + i, BLOCK_SIZE_N * bx + tx * THREAD_SIZE_X + j, N)]) = FETCH_FLOAT4(tmpC[i][j]); } }}

流行歌曲推荐

网络标签：

相关问题